再生水板式换热器微生物污垢热阻的预测
2022-02-24许彤阳王智伟
1 概述
再生水换热设备污垢严重是污水源热泵面临的关键问题之一
。由城市污水处理后的再生水,仍然含有大量微生物、有机污染物和悬浮物,易在流经换热设备表面时产生大量微生物污垢,降低换热设备的换热效率,增大流动阻力,严重影响换热系统的安全和经济运行。
Kern等人
建立了污垢热阻模型,认为污垢热阻随时间的变化是由沉积率与剥蚀率两部分叠加,这就是著名的Kern-Seaton模型,此后的大多数污垢模型是基于这一模型发展的。但是微生物具有活性,问题就变得更为复杂。曹生现等人
基于微生物生长动力学模型建立了工业循环冷却水系统中管壳式换热器微生物污垢的传热传质模型,得到了水质参数与微生物污垢的关联关系,并验证了该模型的准确性。徐志明等人
将Capdeville生物膜增长体系引入Kern-Seaton模型,建立了新的微生物污垢热阻模型,认为微生物污垢的沉积率由活性生物量的累积率和非活性生物量的累积率两部分组成,并采用铁细菌和管式换热装置对模型进行了实验验证。结果表明:除诱导期外,新的微生物污垢热阻模型的计算数据和实验数据的相对误差小于20%。Chen等人
将污水处理厂的铁细菌和硫酸盐还原细菌进行分离和培养,在500 mm×60 mm×50 mm的不锈钢流道中进行了微生物污垢的生长实验,实验结果表明微生物污垢在7~8 d逐渐达到平衡状态。
文孝强等人
搭建了光管污垢实验系统,测量了管壁温度及出入口温度等参数,以3组管壁温度、出入口温度作为预测模型的输入变量,以污垢热阻作为预测模型的输出变量,利用偏最小二乘算法拟合出污垢热阻预测方程。利用实验系统的第2个运行期对预测模型进行了验证,预测结果与实验结果的最大相对误差绝对值在8.5%以内。徐志明等人
以松花江水为冷却水搭建了板式换热器冷却水微生物污垢热阻实验台,测得不同工况下松花江水的水质参数,并以水质参数作为输入变量,建立了偏最小二乘回归模型对微生物污垢热阻进行预测,得到了冷却水板式换热器内微生物污垢热阻的增长规律。王大成等人
研制了循环冷却水动态模拟实验装置,在恒定运行条件下,对微生物污垢热阻进行在线监测及动态模拟,经过分析发现加菌管道的微生物污垢热阻可达1.35×10
m
·K/W,而未加菌管道的微生物污垢热阻最高为4.85×10
m
·K/W,铁细菌和硫酸盐还原菌的存在及其含量是导致微生物污垢热阻增大的直接原因。
婆婆每个月拿着工资,自然有了分寸,对欣欣这个“老板”少了很多挑剔;欣欣也体会家有老人的好处——以前只顾着指责,忘记了同时也在享受。重要的是,从此以后,他们夫妻和婆婆融为一体,找到了家的温暖。
目前,对于微生物污垢生长预测的研究并不少见,但研究对象多为管式换热器、普通板式换热器,换热介质也多采用循环冷却水、天然水。本文研究的换热介质为经污水处理厂处理后的再生水,研究对象为再生水换热系统中常用的宽流道板式换热器。再生水水质参数和水温均较为稳定,且宽流道板式换热器相比于普通板式换热器流道更宽。
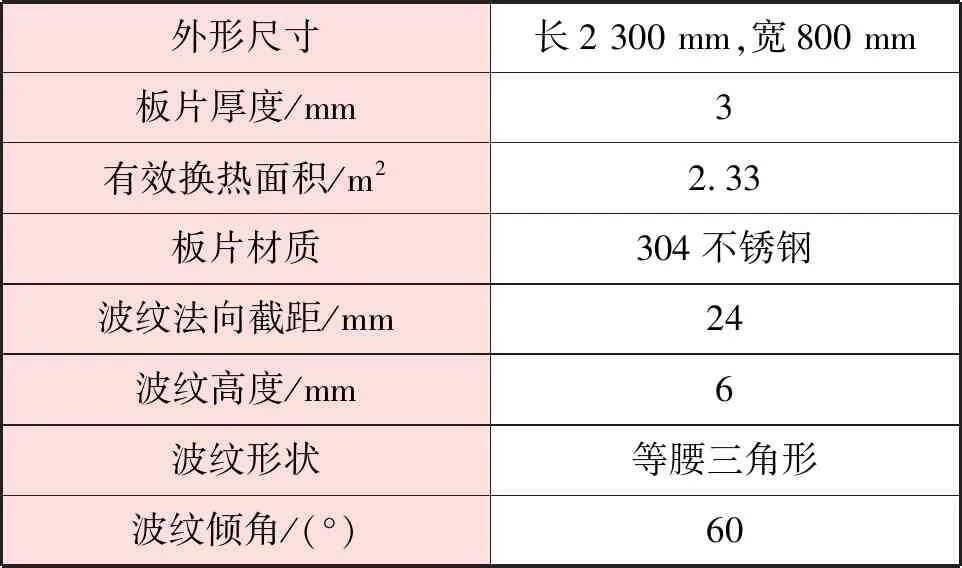
宽流道板式换热器模型(见图1)包含1个换热板片以及1组再生水流道和中介水流道,再生水流道高度30 mm,中介水流道高度18 mm。换热板片参数见表1。
2 最小二乘支持向量机
LS-SVM用平方损失函数代替ε-不敏感损失函数,将标准支持向量回归机中的不等式约束转化为等式约束,得到最小二乘支持向量回归机模型
。训练过程将标准SVM中的凸二次规划问题转化为线性方程组的求解,极大降低了计算的复杂度。
LS-SVM的基础是基于一定数量的已知样本的数据学习过程,目标是通过实验或数值模拟得到的训练数据,拟合一个代理模型来映射一组输入变量和输出变量之间的关系。为了得到最优解,将样本随机分为训练样本、测试样本。
最小二乘支持向量机(Least Squares Support Vector Machine,LS-SVM)是Suykens等人
在1999年提出的支持向量机(Support Vector Machine,SVM)的另一种形式。LS-SVM通过将二次优化问题转化为线性方程组,相比于SVM具有更强的计算优势。
3 微生物污垢热阻预测
3.1 微生物污垢热阻
采用平均绝对百分比误差评价预测模型的预测准确性,平均绝对百分比误差越小,说明预测模型的预测准确性越好。平均绝对百分比误差的计算式为:
3.2 换热器运行参数模拟
采用ANSYS FLUENT 14.5建立板式换热器模型,在已知冷热流体(再生水为热流体,中介水为冷流体)进口温度的前提下,将再生水进口温度及流速为0.4 m/s下的微生物污垢热阻作为初始条件,模拟换热器冷热流体出口温度及再生水侧压力降。中介水侧不考虑微生物污垢热阻。
在数值模拟过程中,冷热流体入口都采用速度入口边界条件(流速为 0.4 m/s)。西安地区污水处理厂再生水冬季水温为12~20 ℃,比环境温度高8~17 ℃
。因此,再生水设置了3种进口温度,分别为20、18、15 ℃。中介水设置了2种进口温度,分别为10、8 ℃。中介水出口采用压力出口边界。
我院应用统计软件SPSS 20.0来进行数据的分析,使用±s的形式对计量资料进行表示,然后通过T值来检验,使用百分号的形式表示计数资料,通过χ2来检验,将P<0.05的情况当成差异具备统计学意义。
本文基于细胞自动机模型、多孔介质导热模型,分别模拟再生水水质及不同温度、时间条件下,流速为0.4 m/s时微生物污垢的厚度及热导率,进而计算微生物污垢热阻(称为计算值)。针对再生水放热工况,采用ANSYS FLUENT建立宽流道板式换热器模型,模拟换热器冷热流体出口温度及再生水侧压力降。将微生物污垢热阻计算值、模拟结果作为微生物污垢热阻预测模型(采用最小二乘支持向量机建立)的训练样本、验证样本,采用平均绝对百分比误差评价预测模型的准确性。

板式换热器模型采用六面体结构进行网格划分,网格大小为8 mm,网格数量为1 558 644个。模拟过程中的计算设置如下:求解器采用压力基求解器,计算模型选用Realizable
-
模型,采用非平衡壁面函数,用SIMPLE算法进行压力与速度的耦合,各控制方程的离散均选用二阶迎风格式。能量方程的相对残差小于10
,其他控制方程的残差小于10
。迭代设置为1 000步。
3.3 微生物污垢热阻预测模型
预测模型的使用场景为:上述宽流道板式换热器,冷热流体进口流速均为0.4 m/s。预测模型的输入参数为换热器冷热流体进出口温度以及再生水侧压力降,输出参数为微生物污垢热阻。选取35组换热器运行参数模拟结果,28组作为预测模型的训练样本,剩余7组作为验证样本。
式中
——平均绝对百分比误差
预测模型训练时,先对样本数据进行预处理,然后选择核函数,最后确定正则化参数及核参数。
③ 正则化参数和核参数的确定。在训练模型时,正则化参数和核参数决定了训练误差和泛化能力
。本文采用交叉验证法进行正则化参数和核参数确定,最终确定正则化参数为650,核参数为0.05。
② 核函数的选择。核函数的选择在算法的实现过程中至关重要。研究认为,径向基函数比线性函数好
,比Sigmoid函数精度高
,而多项式核函数在阶次较高时还会导致数值计算困难。因此,本文选用径向基函数作为核函数。
① 样本数据的预处理。为加快预测模型的训练速度,提高预测模型的精度,先对样本数据进行归一化处理。常用的归一化方法有Min-Max标准化法、Z-score标准化法。本文选用Min-Max标准化法处理样本数据,把样本数据均归一到[0,1]。
刘训峰在主题报告中,回顾了上海华谊化工60年的创业史、奋斗史、发展史,尤其是改革开放40年来改革、创新、发展与调整的历程,在总结近10年发展成效的基础上,对集团未来发展提出了明确目标与要求。他强调,过去60年,华谊集团在党的坚强领导下,依靠广大员工艰苦创业、发展壮大。面对新时代、新挑战,我们要着力把党的政治优势和组织优势转化为企业发展的竞争优势,更加注重提升党建引领能力。
4 预测准确性评价
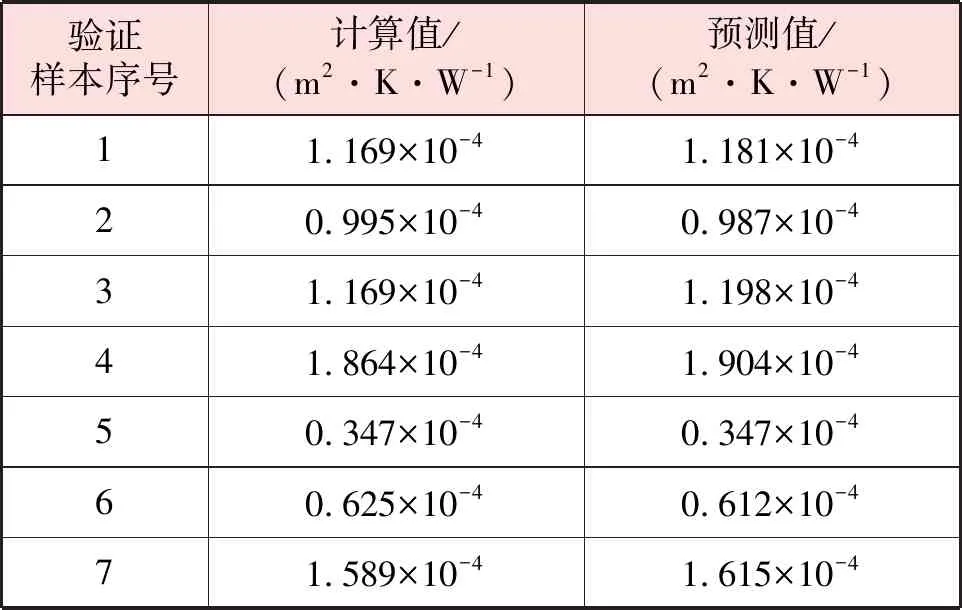
计算值与由7组验证样本得到的预测值见表2。
采用细胞自动机模型
研究再生水水质及不同温度、时间条件下,流速为0.4 m/s时微生物污垢的生长机理。微生物污垢的细胞自动机模型主要包含活细胞、死细胞、胞外不溶性分泌物、胞外可溶性分泌物和营养基质5种组分,按照生物量的转移规则求解了各组分的控制方程,进而得到微生物污垢厚度随温度和时间的变化。并结合多孔介质导热模型,得到微生物污垢热导率随温度和时间的变化。根据微生物污垢厚度与热导率,可计算得到微生物污垢热阻(以下称为计算值)。
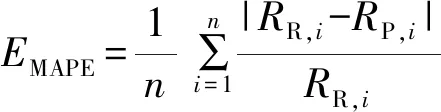
(1)
通过理论及实验比较分析表明,参与实验过程的4个垂直搜索引擎都是非常优秀的,且各具特色。有些搜索引擎对某个专业领域的搜索、查询结果不一定能获得最佳的效果,问题主要出在专用与通用的处理机制方面;有些搜索引擎搜索、查询结果范围不广,主要是没有建立的效的外链接机制。同时,也验证了本文设计的垂直搜索引擎在优化系统结构的同时,抓住了主题爬虫这个主要环节,确保了搜索的精确度,在应用方面更具针对性。
——验证样本数量
R,
——第
组验证样本的污垢热阻的计算值,m
·K/W
采用SPSS 19.0软件对数据进行分析处理,计量资料以(均数±标准差)表示,两个样本均数比较采用t检验,多于两组样本均数的比较,采用方差分析(ANOVA);计数资料以(n,%)表示,采用χ2检验,以P<0.05表示差异具有统计学意义。
P,
——第
组验证样本的污垢热阻的预测值,m
·K/W
(2)若控制有眼/无眼性状的基因位于常染色体上,请用上表中杂交子代果蝇为材料设计一个杂交实验来确定无眼性状的显隐性(要求写出杂交组合和预期结果)________________________________________________________________________________。
将表2数据代入式(1),可计算得到平均绝对百分比误差为1.48%,说明预测模型的预测准确性比较高,可用于工程应用。
对于直流电机这种复杂的控制系统而言,在响应的不同阶段或受到外界扰动时,传统的控制规则很难满足控制精度的要求,表现为稳定性差或超调过大。本文通过设计一种自调整因子α,并将α作用于KP、KI、KD的模糊规则上,实现模糊规则的自适应调整,从而使系统具有更快的响应速度和更小的超调。下面以KP的模糊规则为例,说明自调整因子α的设计原理。
5 结论
预测值与计算值的平均绝对百分比误差为1.48%,预测模型的预测准确性比较高,可用于工程应用。
[1] WANG F,CHEN J,HONG H,et al. Pollutant removal and membrane fouling in an anaerobic submerged membrane bioreactor for real sewage treatment[J]. Water Science & Technology,2014(8):1712-1719.
[2] KERN D Q,SEATON R E. A theoretical analysis of thermal surface fouling[J]. Chemical Engineering Progress,1959(5):258-262.
[3] 曹生现,孙嘉伟,刘洋,等. 微生物污垢形成的传热传质模型[J]. 工程热物理学报,2012(6):1023-1026.
[4] 徐志明,沈艺雯,张一龙,等. 基于Kern-Seaton模型结合Capdeville生物膜增长体系建立的微生物污垢模型[J]. 化工学报,2016(7):2998-3003.
[5] CHEN X,YANG Q,WU R,et al. Experimental study of the growth characteristics of microbial fouling on sewage heat exchanger surface[J]. Applied Thermal Engineering,2018,128:426-433.
[6] 文孝强,苗庆龙,孙灵芳. 换热器污垢特性的建模与预测[J]. 化工机械,2014(6):699-704.
[7] 徐志明,文孝强,郑娇丽,等. 板式换热器冷却水污垢热阻预测的偏最小二乘回归法[J]. 化工学报,2011(6):1531-1536.
[8] 王大成,钱才富,曹生现. 换热设备微生物污垢的动态模拟及影响因素分析[J]. 化工学报,2013(8):1934-1938,1942.
[9] SUYKENS J A K,VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters,1999(3):293-300.
[10] 曾杰,张华. 基于最小二乘支持向量机的风速预测模型[J]. 电网技术,2009(18):144-147.
[11] LASPIDOU C S,RITTMANN B E. Modeling the development of biofilm density including active bacteria, inert biomass, and extracellular polymeric substances[J]. Water Research,2004,38:3349-3361.
[12] 李扬. 直接式污水源热泵污垢生长特性研究(硕士学位论文)[D]. 西安:西安建筑科技大学,2015:34-39.
[13] KEERTHI S S,LIN C J. Asymptotic behaviors of support vector machines with Gaussian kernel[J]. Neural Computation,2003(7):1667-1689.
[14] LIN H T,LIN C J. A study on sigmoid kernels for SVM and the training of non-PSD kernels by SMO-type methods[EB/OL]. [2003-03-10]. http://www.csie.ntu.edu.tw/~cjlin/papers.html.
[15] 周辉仁,郑丕谔,任仙玲. 最小二乘支持向量机的参数优选方法及应用[J]. 系统工程学报,2009(2):248-252.