断层破裂速度对地震动及其地震灾害影响的有限单元法模拟
2022-02-23王松朱守彪
王松,朱守彪
应急管理部国家自然灾害防治研究院,北京 100085
0 引言
地震学研究表明,天然地震断层的破裂传播速度不尽相同,大多数地震的破裂速度是介质剪切波速度的0.8倍(Heaton, 1990),但也有一些地震,其破裂速度超过了介质的剪切波速度,如:1979年美国 Imperial Valley 地震(MW6.5)(Archuleta, 1984; Spudich and Cranswick,1984)、1999年土耳其Izmit地震(MW7.6)(Bouchon et al.,2001, 2002; Sekiguchi and Iwata, 2002)、1999年土耳其 Düzce地震(MW7.1)(Bouchon et al., 2001; Birgöen et al.,2004; Bouin et al., 2004; Ozgun Konca et al., 2010)、2001年中国昆仑山口西地震(MW7.8)(Bouchon and Vallée, 2003; Antolik et al.,2004; Robinson et al., 2006; Vallée et al., 2008; Walker and Shearer, 2009)、2002年美国阿拉斯加Denali地震(MW7.9)(Dunham and Archuleta, 2005; Ellsworth et al., 2004; Asano et al.2005;Walker and Shearer, 2009)、2010年青海玉树地震(Wang and Mori, 2012; Yokota et al., 2012; 张丽芬等, 2014)以及2013年美国阿拉斯加Craig地震(MW7.5)(Yue et al., 2013)、2018年印度尼西亚巴鲁地震(MW7.5)(Bao et al., 2019).这类地震认为是超剪切破裂地震.当发生超剪切地震破裂时,不同时刻所有破裂尖端产生的地震波同时到达马赫锥,并发生相长干涉,导致马赫波振幅显著增大,相应的地震动幅度也大大增加,从而加重地震灾害 (Bernard and Baumont, 2005;Dunham and Bhat, 2008;Andrews, 2010;Cruz-Atienza and Olsen, 2010;胡进军和谢礼立, 2011;Vallée and Dunham, 2012;Yue et al., 2013; 徐建宽, 2014; 朱守彪等, 2017;朱守彪和袁杰, 2018).此外,近期的研究还表明,地震破裂的速度没有禁区,可以从亚瑞雷波(sub-Rayleigh wave)速度一直连续变化到超剪切波速度(如:Bizzarri and Das, 2012;Liu et al., 2014; Weng and Ampuero, 2020).而之前一度认为断层的破裂速度有一个禁区(forbidden zone),即破裂速度不可能介于瑞雷波与剪切波速度之间(Andrews,1976; Burridge et al.,1979; Broberg, 1999;Bizzarri and Das, 2012).
然而,断层破裂速度与地震动及地震灾害之间究竟有什么样的关系?这个问题至今未见前人进行过系统的分析和定量研究.为此,本文设定一个矩震级为7.0的系列地震,并设这些地震断层的破裂速度由小到大变化(即从亚剪切破裂变换到超剪切破裂);研究在地震震级都相同的情况下,考察只是由于断层的破裂速度发生改变,不同地震造成的地震动及强地面运动加速度(PGA)幅值的变化及其在空间的分布,由此进一步分析矩震级相同的地震由于破裂速度不同造成的灾害程度的差异.无疑,本研究可以加深理解断层破裂速度对于地震灾害的影响.
1 有限元模型
本文试图模拟在地震震级不变的情况下,断层的破裂速度从小到大变化.由于在数值模拟中,断层的破裂速度是不容易控制的,因此研究中参考前人的方法采用运动学模型(如:Aagaard and Heaton, 2004; Bernard and Baumont, 2005),即设断层上的质点产生位错脉冲,激发地震波.尽管位错传播的速度不同,但断层长度及位错量大小的累积是相同的,从而保证不同的破裂传播速度情况下,其矩震级都是相同的.实际计算中,采用有限单元方法进行定量模拟分析.
1.1 基本模型参数
为抓住主要矛盾,同时也节省计算资源,研究中将实际地震的三维空间结构简化为二维模型,将复杂的断层几何简化为一条直线.图1展示有限元模型、断层几何以及边界条件.图中有限元模型的几何尺度为110 km×110 km的正方形,图中直线表示断层,其长度为40 km.破裂起始位置处于断层的中央,图中用红色五角星表示.在断层破裂过程的动力学模拟中,很难随意控制断层自发破裂的传播速度,因此为实现断层破裂速度的任意控制,研究中采用运动学的方法.即在断层面上的每个节点上加载位错脉冲,通过控制位错脉冲前行的速度来控制断层破裂的速度.同时,为了尽量减少地震波在边界上的反射所造成的数据污染,模型边界上采用了吸收边界(见图1中绿色边界部分)(朱守彪等, 2017; 袁杰和朱守彪, 2017).
本文实际计算利用有限元商业软件(ABAQUS)来实现,其中模拟正常地震时用ABAQUS/Explicit(显式动力学算法)进行计算,模拟产生慢地震时(即断层破裂的总时间为10天),选用ABAQUS/Implicit(隐式动力学算法)进行计算.另外,为了尽量减小有限元网格大小变化引起的计算误差,文中采用大小均匀的正四边形单元(100 m×100 m).整个模型的有限元网格节点数为1217000,单元数为1214400.

图1 有限元模型的几何以及断层位置中间黑色直线表示断层,断层长度为40 km,断层为右旋走滑断层,红色五角星为破裂起始位置;模型四周绿色区域为吸收边界.Fig.1 The geometry and fault location of the finite element modelThe black line in the middle is the fault with the length of 40 km. The fault is a right-handed strike-slip fault, and the red star stands for the rupture starting position, while the green area around the model represents the absorbing boundary.
为了简化计算,本文所有模型中全部采用均匀各向同性的线弹性介质,具体材料参数选定为,介质密度2700 kg·m-3,P波速度VP=5196 m·s-1,S波速度VS=3000 m·s-1.有限元模型中,所有破裂(包括亚剪切破裂及超剪切)的破裂总时间长度为30 s;显式动力学中计算的时间步长为10-3s;但模拟慢地震的总时间为10天(864000 s),计算时间步长为1000 s.
1.2 震源参数
为了模拟断层破裂时产生的地震动过程,震源参数的选择非常重要.参照前人的方法,本文的震源时间函数采用Schmedes等(2010)中的运动源模型(见公式(1)),其变化趋势类似于Yoffe的震源时间函数(Yoffe, 1951).
(1)
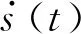
文中设定断层上每个单元节点破裂时,有如图2b所示的滑移位移时间函数.实际计算时,按照破裂速度大小,将滑移位移时间函数离散化后一一施加到所有的断层节点上(不同位置的节点起始点不同),这样就可以形成地震破裂过程.此外,图2b显示最终位移为1 m,这样位错量即为2 m.对于一般的地震,假定断层深度为15 km,其地震矩为2.916×1019N·m,因而矩震级是MW7.0.研究中,对于所有的破裂模型,尽管断层的破裂速度不同,但其矩震级都是相同的(包括慢地震).下文中,通过改变断层的破裂速度,考察不同模型造成的地震动差异,定量给出PGA和PGV在空间的展布,进而研究地震灾害分布情况.
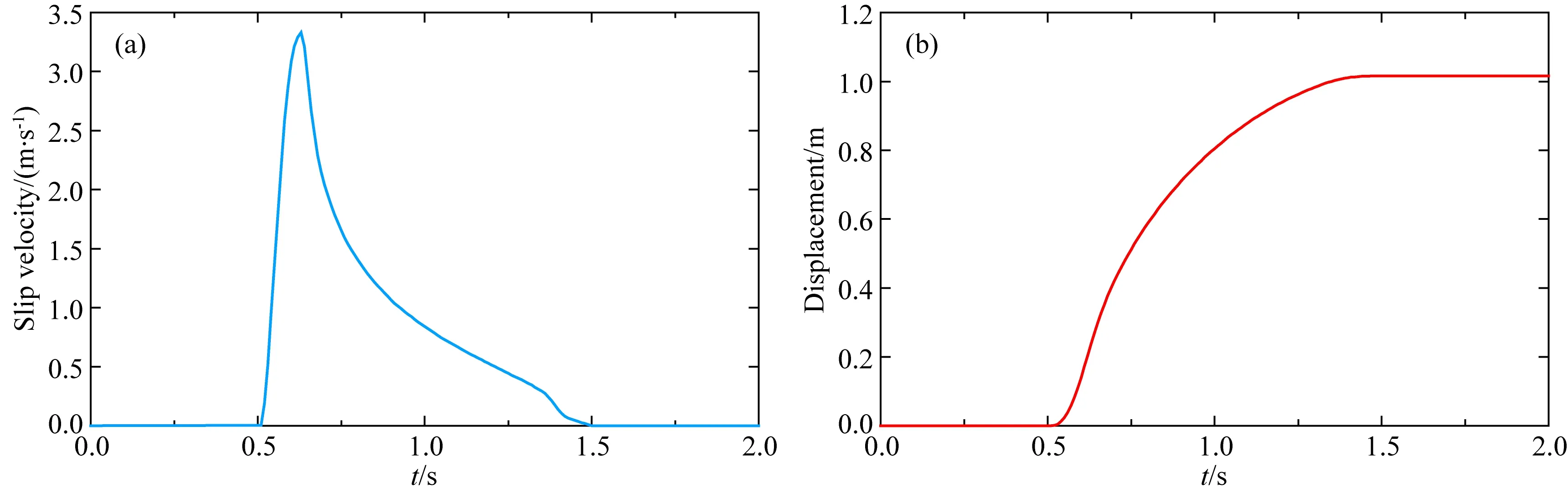
图2 震源时间函数变化曲线图(a) 表示断层上节点滑移速率随着时间的变化; (b) 表示断层面每个节点上其位移随着时间的变化曲线.Fig.2 Curves of source function with time(a) Slip rates change with time at each node on the fault; (b) Displacements vary with time at each node on the fault plane.
2 模拟结果
通过对实际地震的研究,发现不同的地震其断层的破裂速度是不同的.下面利用有限元方法,研究在不同的断层破裂传播速度的情况下,地震动过程及PGA在空间的展布及其地震灾害分布情况.
2.1 断层破裂过程
为研究不同的断层破裂速度对地震动的影响,本文以介质的剪切波速度(VS)为分界线,分别设定亚剪切破裂和超剪切破裂两种情况来进行数值模拟.计算中首先将亚剪切破裂速度分别设定为0.6、0.7、0.8及0.9倍的剪切波速度.图3表示在这种情况下,模拟给出的不同时间的加速度空间分布等值线云图快照.图中从左至右为不同的破裂速度(0.6VS、0.7VS、0.8VS及0.9VS),从上到下分别为不同的时刻(从第1 s 到第8 s)的快照.图中清晰地显示,随着时间的推移,不同破裂速度的破裂都是由断层中心向两侧传播;在同一时刻,破裂速度越大的破裂,其地震动加速度也越大,即震害会越严重(朱守彪和袁杰, 2018).
当破裂速度大于剪切波速度,即产生超剪切破裂时,不同的断层破裂速度、在不同时刻的加速度快照如图4所示.图中显示,当破裂为超剪切破裂时,都产生了马赫波,这与前人的结果是一致的(Bernard and Baumont, 2005; Andrews, 2010; Vallée and Dunham, 2012; Yue et al., 2013; 朱守彪等, 2017).同时,还可以看到,随着破裂传播速度的增大,马赫角逐渐减小(Bernard and Baumont, 2005).
对比图3与图4可以清楚地看到,当发生亚剪切破裂时,地震波主要集中在断层附近及破裂前端,加速度的高值区范围较小;但是,当产生超剪切破裂时,由于马赫波的形成,加速度的图像发生了很大的改变,加速度的高值区的空间范围明显增大,这时的地震灾害会大大增加.
2.2 PGA和PGV空间分布
由于地震灾害主要是由于地震产生的力的作用导致的,而力的来源是地震动加速度.所以,为更加清楚地显示不同的断层破裂速度造成的地震灾害,下面分别给出在不同的破裂速度时,强地面运动峰值加速度(PGA)和峰值速度(PGV)在空间的分布.
图5是在不同破裂速度模型中的PGA空间分布.图中显示,当破裂速度为亚剪切破裂时,破裂速度越大,PGA的峰值越高,并且分布范围也越大,即地震灾害随着破裂速度的增大而加剧;同时图中还可以看到,超剪切破裂的PGA总体上比亚剪切破裂的PGA峰值高、展布范围大,即超剪切破裂造成的地震灾害比亚剪切破裂要严重(Bernard and Baumont, 2005; Dunham and Bhat, 2008;Andrews, 2010).图6中的PGV空间分布也有类似的规律.
值得注意的是,我们可以从PGA空间分布上看到,超剪切破裂明显降低了断层附近最强烈的峰值速度,但在一些距离较远的地方增加了速度量值,这一结果与前人模拟给出的结果具有一致性(Bernard and Baumont, 2005; Andrews, 2010).
在亚剪切波速情况下,破裂发生时的定向波束集中在断层投影周围的一个狭窄方位范围内.在断层附近峰值速度本来很强烈,但是由于破裂波束是发散的,故而衰减很快,振幅剧烈部分集中于断层附近.
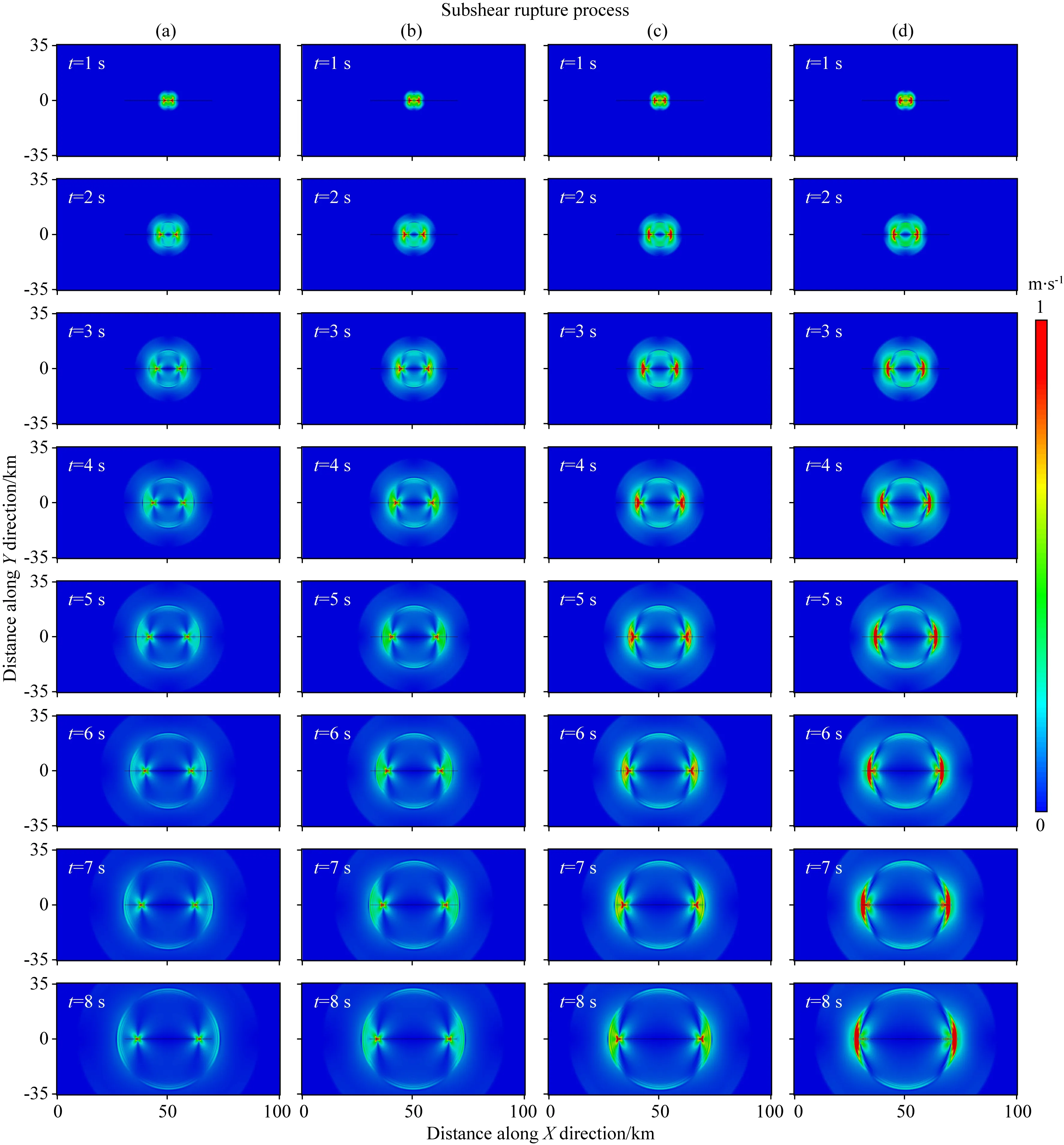
图3 当断层破裂速度都为亚剪切破裂时,不同破裂速度模型的速度等值线云图在不同时刻的快照(a) Vr= 0.6VS(第一列图); (b) Vr= 0.7VS(第二列图); (c) Vr= 0.8VS(第三列图); (d) Vr= 0.9VS(第四列图).Fig.3 Snapshots of velocity cloud diagrams for different rupture velocity models when the fault rupture velocities are all at sub-shear ruptures(a) Vr=0.6VS (the first column); (b) Vr= 0.7VS (the second column); (c) Vr= 0.8VS (the third column); (d) Vr= 0.9VS (the fourth column).

图4 当断层破裂速度都为超剪切破裂时,不同破裂速度模型的速度云图快照(a) Vr=1.3VS(第一列图); (b) Vr=1.5VS (第二列图); (c) Vr=1.7VS (第三列图); (d) Vr=1.9VS (第四列图).Fig.4 Snapshots of velocity cloud diagrams for different rupture velocity models when the fault rupture velocities are all at supershear ruptures(a) Vr=1.3VS (the first column); (b) Vr=1.5VS (the second column); (c) Vr=1.7VS (the third column); (d) Vr=1.9VS (the fourth column).

图5 不同破裂速度时的PGA分布图(a—e)是亚剪切破裂时的PGA分布;图(f)是破裂速度为剪切波速时PGA分布,图(g—j)在发生超剪切破裂时的PGA分布.Fig.5 PGA distributions at different rupture speedsFigures (a—e) denote the PGA distributions when subshear ruptures occur; Figure (f) is the PGA distribution when the rupture velocity is at the shear wave velocity, and figures (g—j) are the PGA distributions when the super-shear ruptures occur.
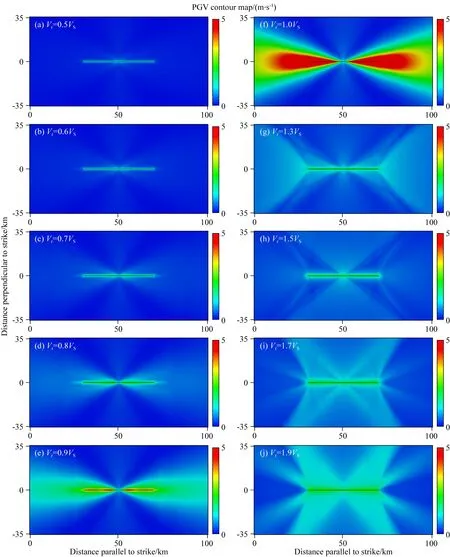
图6 不同破裂速度时的PGV分布图(a—e)是亚剪切破裂时的PGV分布;图(f)是破裂速度为剪切波速时PGV分布; 图(g—j)在发生超剪切破裂时的PGV分布.Fig.6 PGV distribution at different rupture speedsFigures (a—e) denote PGV distribution when subshear ruptures occur; Figure (f) is the PGV distribution when the rupture velocity is at the shear wave velocity, and figures (g—j) are the PGV distributions when the super-shear ruptures occur.
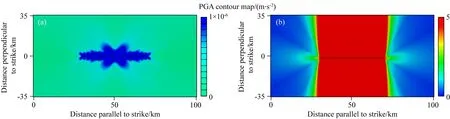
图7 2个极端模型中PGA空间分布图(a) 慢地震; (b) 破裂速度为无穷大的模型.Fig.7 PGA distributions in two end members(a) Slow event; (b) Model with infinity rupture velocity.

图8 当破裂速度分别为以及1.5VS时不同时刻的加速度快照(a) 当破裂速度为1.3VS时,出现了马赫波; (b) 当破裂速度为时,未见剪切马赫波;(c)当破裂速度为1.5VS时,再次出现了马赫波.Fig.8 Snapshots of particle accelerations at different moments when the rupture velocity is 1.3VS, and 1.5VS, respectively(a) When the rupture velocity is 1.3VS, Mach waves appear; (b) When the rupture velocity is the Mach waves are not observed; (c) When the rupture velocity is 1.5VS, Mach waves appear again.
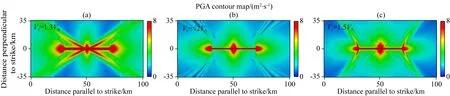
图9 破裂速度分别为和1.5VS时PGA分布图(a) 破裂速度为1.3VS ; (b) 破裂速度为 破裂速度为1.5VS.Fig.9 PGA distributions when the rupture velocity is 1.3VS, VS and 1.5VS, respectively
在超剪切情况下,马赫波形成一束平行射线.马赫波束也可以被认为是一种方向性效应,因为它取决于震动源的相干性.马赫波的振幅是恒定的,直到在更大的距离,由于衍射和散射而不断衰减(Bernard and Baumont, 2005).
此外,图中还展示了一个十分显著的特征,当断层的破裂速度等于介质的剪切波速度时,PGA在断层附近的幅值特别大;可以想象这样的地震,其灾害将是特别严重.这种情况在实际天然地震是否产生,是值得今后深入研究的问题.
值得注意的是,超剪切破裂的地震(如破裂速度为1.3VS、1.5VS及1.7VS),地震动在垂直于断层方向的衰减慢,并且随着速度的增大,PGA高值区在空间的分布范围也逐渐增大,即震害也会加剧.
3 讨论
为研究断层不同破裂速度对地震灾害的影响,我们还研究了2个极端破裂速度情况的模型,即一个速度非常小,另一个速度特别大的模型.首先,模拟破裂速度非常缓慢的破裂模型(这种地震通常称为慢地震或慢滑移事件),模拟中所有其他的模型参数都与前文的模型相同.在这种情况下,破裂产生的矩震级仍为MW=7.0不变,即断层上的最终位错大小不变,但破裂的时间设定为10天,此时的断层破裂速度为0.046 m·s-1.通过与上述同样的模拟计算发现,慢地震中PGA 值非常微小,几乎处处为0(见图7a).这时除了断层两侧的位错可能会对建筑物等带来损坏外,地震波几乎不产生任何破坏性影响.
另一个极端模型就是断层破裂速度为无穷大的情况,这时断层上所有节点同时发生破裂.同样,保持矩震级为MW=7.0不变,断层上最终位错与前面的模型保持一致.通过相同的模拟计算得到,此时PGA比较大,且主要分布在断层的两侧(见图7b).通过对照比较发现,我们的模拟结果与前人的完全一致(Bernard and Baumont, 2005).由此可见,这时断层两侧地震灾害较大,震灾严重地区的空间分布范围也比较广泛.

关于剪切马赫波消失的现象,可以从Weertman(1996, 2004)推导的断层破裂速度与应力场之间的关系中得到解释.
根据Weertman(1996, 2004)的理论推导,在均匀各向同性介质中,若断层的破裂速度是V,u是x方向的位移(平行于接触面),v是y方向位移(垂直于接触面),下标S的参数与横波有关,下标L的参数与纵波有关,则关于纵波和横波的水平和竖直方向的位移可分别表示如下:
(2)
(3)
(4)
(5)
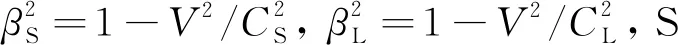
这样,关于横波和纵波的剪切应力可以用以下公式表达.
(6)
(7)
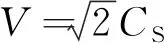
4 结论
本文利用有限单元方法模拟了震级为MW7.0时,在不同的断层破裂传播速度情况下,相应的地震动及其PGA在空间的分布特征,主要结论如下.
地震动及其强地面运动加速度空间分布受断层破裂速度的影响很大.总体来说,断层破裂速度越快,PGA峰值越大、展布的范围也越大,因而造成的地震灾害也会越严重;特别是当产生超剪切破裂时,地震动及其造成的地震灾害远远大于亚剪切破裂的同震级地震.
但是,当断层的破裂速度正好等于介质的剪切波速度时,近断层处的PGA幅度特别大,甚至超过超剪切破裂的情况.然而,当破裂速度为Eshelby速度时,剪切马赫波消失,但PGA并没有大幅度减小,其震害也没有显著减轻.另外,若破裂速度十分缓慢,PGA的幅值几乎为0,所以慢地震地震动几乎不会对建筑物造成影响.
致谢两位审稿专家提出了诸多宝贵意见和建议,在此表示感谢.
