俯冲带库仑楔形体力学

胡岩

1 中国科学技术大学地球和空间科学学院，合肥 230026 2 中国科学技术大学蒙城地球物理国家野外科学观测研究站，安徽蒙城 233527 3 中国科学院比较行星学卓越创新中心, 合肥 230026

0 引言

楔形体理论主要研究剖面呈三角形的地质块体受力状态.从山前推覆构造到俯冲带弧前增生楔，楔形体普遍存在.然而如何描述楔形体内部应力状态，进而分析楔形体内部变形(破裂过程)和岩石性质以及断层强度之间的关系，一直是地学研究关注的问题.针对不同楔形体材料以及边界条件人们先后提出多个应力解析解(例如，Davis et al., 1983; Dahlen, 1984, 1990; Dahlen et al.，1984; Liu and Ranalli, 1992; Platt, 1993；Yin, 1993, 1994; Williams et al., 1994；Yin and Kelty, 2000).这些解析解均假设静力平衡条件，而忽略惯性力项.虽然考虑惯性力项和其他复杂性(例如复杂材料性质及其不均一性，底部边界摩擦性质不均一性等)的模型可以更真实地模拟俯冲带增生和剥蚀过程，但是求解过程耗时并且难以获得解析解.本文首先简要介绍部分已发表的应力解析解，然后详细介绍基于理想弹塑性楔形体的应力函数解析解(Hu and Wang，2006).最后介绍基于该解析解提出的动态库仑楔形体理论(Wang and Hu，2006).

1 楔形体应力解析解

1.1 弹性楔

Yin(1993,1994)研究了剖面为三角形的弹性楔形体内部应力状态(图1a).该楔形体底部为静态摩擦边界，有效摩擦系数为μ′b.在左边界垂直于表面的压力随深度线性增加.楔形体上表面为自由空气界面.Yin和Kelty(2000)进一步研究了这个三角形楔形体，假设左边界压力变化为深度的二次函数.具体推导解析解过程请参考Yin和Kelty(2000)，这里介绍该文章得出的最终解.

+(1-λ)ρwgsinαx,

(1)

(2)

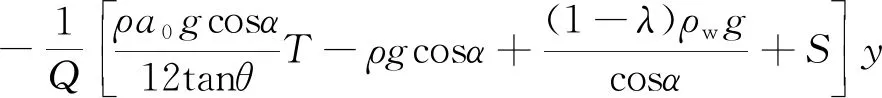
(3)

其中，α和β分别为上表面坡度角和下表面的倾角，θ=α+β，σx和σy分别为x和y方向的正应力(本文中，压应力为负，拉张应力为正)，τxy为剪应力，ρw和ρ分别为水和岩石的密度，g为重力加速度，以及如下关系式：

(4)

其中，Xe和Ye分别为重力和孔隙流体产生的x和y方向的体力，l=-sinθ,m=cosθ.Yin和Kelty(2000)通过以上应力解析解很好的解释了美国夏威夷毛纳洛基拉韦厄裂谷地区(Mauna Loa-Kilauea)正断层和逆冲断层共同存在的现象，然而该解析解比较复杂，难以方便地应用.

Liu和Ranalli(1992)研究了梯形形状的弹性楔形体内部应力状态.不同于Yin和Kelty(2000)只有左侧边界施加外力，该楔形体左右边界压力均为深度的二次函数.其他边界条件以及推导过程和Yin和Kelty(2000)类似，但是得出的解析解比(1)—(4)更复杂.因为篇幅有限，本文不再累述.

图1 楔形体应力解析解和海沟增生楔地震反射剖面[(a) 修改自Yin and Kelty(2000)图3.(b)来自Hu and Wang (2006)图1b.(c)来自Wang and Hu (2006)图2a](a)有限长(X0)弹性三角形楔形体(Yin, 1993,1994; Yin and Kelty, 2000).左边界压力Fx为深度的函数.底部为静态摩擦边界.(b)无限长理想弹塑性楔形体(Hu and Wang, 2006).其中α和β分别为上表面坡度角和下表面倾角，ρw和ρ分别为水和岩石的密度，g为重力加速度.σn和τn分别为下表面正应力和剪应力.(c)日本南海海沟地震反射剖面(Park et al., 2002).Fig.1 Analytical stress solutions in the wedge and a seismic reflection profile in an accretionary prism [(a) Modified from Fig.3 in Yin and Kelty (2000). (b) From Fig.1b in Hu and Wang (2006). (c) From Fig.2a in Wang and Hu (2006)](a) An elastic triangle-shaped wedge with a limited length (X0) (Yin, 1993,1994; Yin and Kelty, 2000).The external force Fx normal to the left boundary is a function of the depth. A static friction law is applied to the lower boundary. (b) Elastic perfectly-plastic wedge with infinite length (Hu and Wang, 2006). α and β represent the surface slope angle and basal dipping angle, respectively. ρw and ρ represent the water and rock density, respectively. g is the gravitational acceleration. σn and τn represent the normal and shear stress at the lower boundary. (c) Seismic reflection profile in the Nakai trough in Japan (Park et al., 2002).

1.2 临界理想塑性楔

从20世纪80年代开始，研究者先后发表了多篇文章讨论楔形体(图1b)在临界破裂条件下应力状态(Davis et al., 1983; Dahlen, 1984，1990; Dahlen et al., 1984; Zhao et al., 1986; Breen and Orange, 1992; Willett et al., 1993; Wang and Davis, 1996).经典临界楔形体理论描述了理想库仑塑性楔形体应力状态.库仑破裂准则定义了楔形体产生塑性破坏的应力屈服条件.应力在屈服面上时楔形体处于临界破裂状态.当实际应力小于屈服应力，楔形体处于弹性稳定状态；当应力大于屈服应力，楔形体则处于破坏失稳状态.

本文主要介绍Dahlen(1984)推导的经典临界楔形体理论.楔形体边界条件和1.1节介绍的弹性楔形体类似.楔形体内部孔隙水压P基于Hubbert-Rubey流体压力比定义如下(Davis et al., 1983)：

(5)

其中λ为孔隙流体压力比，D为水深.底部边界满足静态摩擦条件τn=-μ′b(σn+P)，其中μ′b为有效摩擦系数，σn和τn分别为底部正应力和剪应力.如果楔形体为均一库仑塑性材料并且内聚力S0为深度的函数，我们可以得到：

S0=η(1-λ)μρgycosα,

(6)

其中η为无量纲常数，μ=tanφ为楔形体内摩擦系数，φ为内摩擦角.基于应力摩尔圆(图2)，应力和角度满足以下关系：

图2 临界破裂状态下楔形体应力摩尔圆σ1和σ3分别为最大和最小主压应力，φ为内摩擦角，ψc为最大主压应力和上表面的夹角，r为摩尔圆半径.Fig.2 Mohr circle of a critical wedge on the verge of failureσ1 and σ3 represent the maximum and minimum principal compressional stress. φ represents the internal friction angle. ψcrepresents the angle between the maximum principal compressional stress and the surface. r is the radius of the Mohr circle.

(7)

(8)

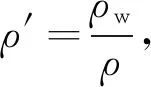
(9)

ψc由(10)式计算得到：

(10)

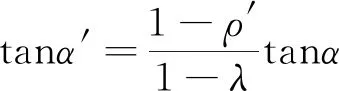
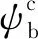
(11)

以Dahlen(1984)文中的楔形体为例，该楔形体几何形状为地表坡度α=4°,底部边界倾角β=4.2°.需要说明的是，地壳岩石的内摩擦系数μ一般小于1.由于经典临界楔形体相关文章(例如，Davis et al., 1983; Dahlen, 1984)均采用μ=1.1.为了更方便读者对比经典解析解和下文介绍的应力解析解，这里也假设μ=1.1.具体选取什么内摩擦系数不会影响本文的结论.假设孔隙流体压力比λ=0.8，则当底部边界有效摩擦系数为μ′b=0.17时，该楔形体处于挤压型临界状态(图3a).楔形体最大主压应力呈近水平状态，可能产生逆冲型破裂(图3a虚线表示可能的破裂方向).当μ′b减小后，楔形体进入稳定状态.这时解析解(8)式不再适用.只有当μ′b=0.017时(图3e)，楔形体主压应力呈近垂直状态.楔形体达到拉张型临界破裂状态，其内部应力可以被(8)式描述.这时楔形体可能产生拉张型正断层(图3e虚线示意可能的正断层破裂方向).当μ′b大于0.17或者小于0.017时，楔形体处于破裂失稳状态，解析解(8)式亦不适用.

Hu和Wang(2008)测量了22个俯冲带弧前几何形状.根据经典塑性临界楔形体理论，Hu 和 Wang(2008)认为这些俯冲带大都处于稳定状态，即解析解(8)式并不适用于解释这些俯冲带弧前应力状态.如果假设更软(例如，更小的μ和更高的λ)的楔形体岩石，一些增生楔处于临界拉张型破裂状态，和俯冲带挤压型区域应力环境不一致.这表明经典临界楔形体理论需要进一步完善以更好地解释俯冲带弧前几何形状和构造应力特征.

图3 楔形体内部应力状态随底部有效摩擦系数变化图[修改自Wang and Hu(2006)图7]楔形体参数α=4°,β=4.2°,μ=1.1,λ=0.8保持不变，底部有效摩擦系数μ′b逐渐减小.(a)临界挤压型破裂状态，μ′b=0.17.黑色成对箭头为最大和最小主压应力.虚线为可能的破裂方向.(b)挤压型稳定状态，μ′b=0.1.(c)中性稳定状态，μ′b=0.038.最大和最小主压应力和楔形体上表面夹角为45°.(d)拉张型稳定状态，μ′b=0.028.(e)临界拉张型破裂状态，μ′b=0.017.Fig.3 Stress status in a wedge with a varying basal effective frictional coefficient [Modified from Fig.7 in Wang and Hu (2006)]In this wedge, we keep α=4°,β=4.2°,μ=1.1,λ=0.8 and vary the basal effective frictional coefficient. (a) Compressively critical state. Black paired arrows represent the maximum and minimum principal compressional stresses. Dashed lines represent potential faulting directions. (b) Compressively stable state, μ′b=0.1. (c) Neutral stable state, μ′b=0.038. The angle between the maximum (or minimum) principal compressional stress and the surface is 45°. (d) Extensionally stable state, μ′b=0.028. (e) Extensionally critical state, μ′b=0.017.

2 理想弹塑性楔形体应力解析解

当楔形体处于临界破裂状态时，内部应力同时满足库仑破裂条件和弹性虎克定律.Hu和Wang(2006)研究理想弹塑性楔形体材料并且得到应力函数解析解.该解析解不仅适用于处于临界破裂状态的楔形体，而且适用于稳定状态的楔形体.本文介绍该解析解推导过程.

对于图1b所示楔形体，假设应力函数Φ为：

(12)

其中ki(i=1,2,3,4)为待解参数.则楔形体各边界条件如下.

自由表面满足：

(13)

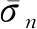
(14)

应力各分量表达式如下：

(15)

将(12)式代入(15)式，得到应力表达式如下：

(16)

基于边界力和内部应力关系(王仁等,1979)，可以得到：

(17)

(18)

将(15)式代入(13)式，得到k1=0，k3=ρ′sinα.综合(5)，(14)，(16)，(17)式和(18)式，可以得到：

(19)

从而可以解出k2和k4分别为：

(20)

(21)

其中

(22)

因此常数a不是一个自由变量，而是和楔形体形状、孔隙流体压力比以及底部摩擦系数有关.基于(21)式，应力分量可以写为：

(23)

比较(8)式和(23)式，当m=mc时，则(23)式和经典临界楔形体解析解完全一致，亦即经典临界楔形体解析解为弹塑性楔形体解析解(23)式的子集.

对于1.2节给出的楔形体例子，当μ′b=0.17或者μ′b=0.017时，m=mc，这时解析解(23)式可以描述楔形体分别处于临界挤压型破裂和临界拉张型破裂状态时的应力分布(图3a和图3e).当μ′b=0.1时，楔形体为挤压型稳定状态，解析解(23)式亦能给出应力分布(图3b).当μ′b=0.038时，楔形体为中性稳定状态，最大和最小主应力与楔形体表面夹角为45°(图3c).当μ′b=0.028时，楔形体为拉张型稳定状态(图3d).

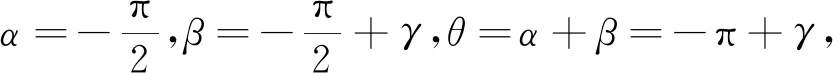
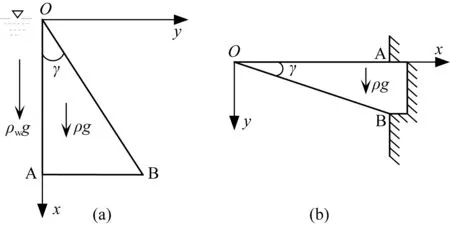
图4 (a)大坝和(b)三角形悬臂梁受力示意图ρw和ρ分别代表水和岩石的密度.g为重力加速度.γ为三角形楔形体夹角.Fig.4 Illustration of the stress status in (a) a dam and (b) a triangle-shaped hanging beamρw and ρ represent the water and rock density, respectively. g is the gravitational acceleration. γ is the angle of the triangle-shaped wedge.

(24)

(24)式与徐芝纶(1979，第58页)给出的解析解一致.

图4b给出悬臂梁的受力示意图.对于该例子，α=0,β=γ,θ=α+β=γ，其中γ为三角形悬臂梁夹角.代入该几何参数可以得到：

(25)

该解析解(25)式与徐芝纶(1979，第67页)给出的解析解一致.

3 动态库仑楔形体理论

弧前增生楔和侵蚀前缘在地震周期的应力演化及其与俯冲界面摩擦性质的关系一直是地学研究的热点问题.虽然不同俯冲带前缘几何形状各不相同，但是总体来说可以分为两部分.以日本南海海沟为例(图1c)(Park et al., 2002)，在俯冲带前缘靠近海沟部分，地震反射剖面显示该部分楔形体发育大量逆冲断层，表明经常产生永久变形，同时地表坡度也比较陡.我们把这部分楔形体称为外部楔形体(Outer wedge).在更靠近内陆部分，楔形体内部缺少强烈的构造活动，该地区沉积层没有被破坏而呈较好的水平分布，其地表坡度角也比较小.我们把这部分楔形体称为内部楔形体(Inner wedge).类似弧前几何形状和构造特征也存在于其他俯冲带，例如，卡斯卡迪亚(Cascadia)(McNeill et al., 1997；Gulick et al., 1998)，阿拉斯加(von Huene and Klaeschen, 1999; von Huene and Raneo, 2003)，莫克兰(Makran)(Kopp et al., 2000；Kukowski et al., 2001)，东北日本(von Huene et al., 1986，1994)，秘鲁(Krabbenhöft et al., 2004)，汤加(von Huene and Scholl, 1991)等.在部分俯冲带，外部和内部楔形体地表坡度角可能不如日本南海海沟(图1c)差异那么大，但是构造差异特征几乎存在于每一个俯冲带前缘.例如在阿留申俯冲带，外部和内部楔形体地表坡度角只相差1°，但是几乎所有的永久变形都发生在靠近海沟近35 km宽度的外部楔形体，而更远离海沟区域35 km宽的内部楔形体几乎没有永久变形(Bruns and von Huene，1986；Scholl et al., 1986).

除了弧前楔形体内部构造特征显著不同，一般认为俯冲界面摩擦性质也具有不均一性.俯冲带断层面可能存在大小形状不一的凹凸体(Bilek and Lay, 2002).凹凸体接触面为黏滑，可以积累应力，孕育地震.凹凸体之间断层面可能为蠕滑，不孕育地震.部分区域可能表现为有条件蠕滑.这些摩擦性质可以用含速率与状态的摩擦(Dieterich，1994；Ruina，1983)描述.总体来说，从海沟沿俯冲界面到深部可以分为三部分(Hu and Wang，2008).在浅部，由于岩石固结程度比较低，这部分断层表现为速度强化.中间部分为生震带，摩擦性质为速度弱化.更深部分由于高温高压条件岩石主要为黏性变形，主要表现为蠕滑.

如何解释弧前构造特征的这些差异性？Byrne等(1988)认为这些构造差异性是由楔形体材料强度不同决定的.内部楔形体结晶基底作为支柱阻碍前缘因为俯冲效应导致的缩短，从而变形主要发生在岩石固结程度低、强度小的外部楔形体.这个理论可以较好地解释部分具有增生楔的俯冲带，但是部分俯冲带(例如阿拉斯加和日本南海海沟)缺少结晶基底或者结晶基底在更靠近内陆方向，该理论则不适用.Kopp和Kukowski(2003)进一步提出岩石固结程度更高、强度更大的沉积岩可以替代结晶基底，同样充当支柱阻碍前缘的永久变形.然而大量研究表明弧前岩石强度和性质的差异可能并不是很大(Lallemand et al.，1994).这些研究只是关注弧前岩石性质的差异而忽略了断层面摩擦性质的差异.

Wang和Hu(2006)提出动态库仑楔形体理论，较好地解释了弧前构造特征以及断层面摩擦性质的差异性.该理论认为外部楔形体对应的底部边界为无震蠕滑带，摩擦性质为速度强化，而内部楔形体对应的底部边界为断层面生震带，摩擦性质为速度弱化.地震发生时，内部楔形体底部边界(生震带)应力降低，摩擦系数减小，楔形体内部经历弹性变形.而外部楔形体底部边界由于速度强化，摩擦系数增加，同时深部生震带同震向上挤压可能导致楔形体孔隙流体压力比升高.综合效应可能导致外部楔形体达到挤压型破裂状态，产生永久变形.

我们以日本南海海沟(图1c)为例进一步解释该理论.基于Wang 和 Hu (2006)，内部楔形体几何形状为α=0.1°,β=9.5°.根据地震反射剖面共轭断层夹角信息，设定内摩擦系数μ=0.7(Wang and Hu，2006).假设孔隙流体压力比λ=0.5，则最大主压应力和上表面的夹角ψ0随底部边界摩擦系数变化而变化(图5b).由于内部楔形体底部边界为生震带，摩擦性质为速度弱化，在地震发生前摩擦系数应该比较低，例如μ′b=0.04.地震发生时，因为速度弱化，断层面摩擦系数降低.假设内聚力系数η=0，则内部楔形体底部摩擦系数沿图5b中黑色虚线向左侧移动，这导致ψ0逐渐增加，即内部楔形体由中性稳定状态(类似图3c)逐渐变为拉张型稳定状态(类似图3d).由于底部摩擦系数实际不可能成为负数，因此内部楔形体永远不可能到达虚线左侧的端点(临界拉张型破裂).地震发生后，由于断层面不再滑动，基于速度弱化摩擦性质，底部断层摩擦系数逐渐增加到地震前稳定状态.如果内部楔形体内聚力系数更高，例如η=0.6，则内部楔形体在地震时更难达到临界破裂状态(图5b灰色实线).因此在整个地震周期，内部楔形体只是在中性状态和拉张型稳定状态间转换，只产生弹性变形，不会产生永久变形.

图5 外部和内部楔形体地震周期应力演化[(a)修改自Wang and Hu(2006)图9a.(b)修改自Wang and Hu (2006)图11a](a)外部楔形体应力演化.楔形体参数α=4.5°,β=6.3°,μ=0.7,η=0保持不变.灰色实线、黑色实线和黑色虚线分别表示孔隙流体压力比λ=0.5,0.8,0.922.(b)内部楔形体应力演化.楔形体参数α=0.1°,β=9.5°,μ=0.7,λ=0.5保持不变.黑色虚线和灰色实线分别表示内聚力常数η=0,0.6.Fig.5 Earthquake-cycle stress evolution in an outer wedge and an inner wedge [(a) Modified from Fig.9a in Wang and Hu (2006). (b) Modified from Fig.11a in Wang and Hu (2006)](a) Stress evolution in an outer wedge. The wedge parameters α=4.5°,β=6.3°,μ=0.7,η=0 keep constant. The gray solid line, black solid line and black dashed line represent λ=0.5,0.8,0.922, respectively. (b) Stress evolution in an inner wedge. The parameters α=0.1°,β=9.5°,μ=0.7,λ=0.5 keep constant. The black dashed line and gray solid line represent the cohesion constant η=0,0.6, respectively.

图6 弧前外部和内部楔形体地震周期应力演化[修改自Wang and Hu (2006)图12](a) 同震时弧前应力分布; (b) 震后弧前应力随孔隙流体压力比以及底部摩擦系数变化; (c) 震间(地震周期中后期)弧前应力状态.Fig.6 The earthquake-cycle stress evolution of the outer and inner wedge in a forearc [Modified from Fig.12 in Wang and Hu (2006)](a) Coseismic stress status in the forearc; (b) Postseismic stress status depending on the changed pore fluid pressure ratio and basal frictional coefficient; (c) Interseismic (middle and late stages in an earthquake cycle) stress status in the forearc.

外部楔形体岩石固结程度相对较低，因此孔隙流体压力比容易受应力条件改变而发生变化.我们假设η=0.由于外部楔形体底部为蠕滑带，摩擦性质为速度强化，地震发生后断层面摩擦系数增加.如果楔形体孔隙流体压力比λ=0.5，则外部楔形体底部摩擦系数沿图5a灰色实线向右侧移动.当μ′b=0.26，外部楔形体达到临界挤压型破裂状态(图5a中灰色实线右侧端点).在此条件下，底部摩擦系数需要增加Δμ′b=0.22.通常底部摩擦系数在地震时可能不会变化那么多.生震带同震滑动不仅导致外部楔形体底部摩擦系数增加，更会挤压外部楔形体，导致孔隙度减少，孔隙流体压力增加，相应增加孔隙流体压力比.如果λ=0.8，则底部摩擦系数只需要增加Δμ′b=0.08就可以达到临界挤压型破裂状态(图5a黑色实线右侧端点μ′b=0.12).如果地震导致孔隙流体压力比达到λ=0.922，当楔形体底部摩擦系数达到μ′b=0.047，亦即相对于震前只需稍微增加Δμ′b=0.007，外部楔形体即达到挤压型临界破裂状态(图5a黑色虚线右侧端点).该状态也是底部侵蚀状态(图5a黑色圆点)，即破裂面平行于下表面，外部楔形体底部物质将被不断剥蚀随着俯冲向深部带入.相对于内部楔形体，较大震级地震就可以使得外部楔形体达到临界挤压型破裂.这很好地解释了外部楔形体大量发育永久变形.

图6进一步阐明弧前应力状态在地震周期的演化.地震发生时(图6a)，生震带摩擦系数降到近似零，内部楔形体仍为稳定状态，产生中性/拉张型弹性变形.而外部楔形体底部因为速度强化，底部摩擦系数增加到0.12，同时内部孔隙流体压力比λ增加到0.8，楔形体达到临界挤压型破裂.地震以后，生震带逐步积累应力，其摩擦系数亦逐步增加至地震前状态(例如图6b中μ′b=0.02).内部楔形体逐渐由中性稳定状态变为挤压型稳定状态.而外部楔形体由于孔隙度逐渐恢复，λ逐渐减小，其底部摩擦系数因为速度强化而逐渐减少，内部应力状态由地震时临界挤压型破裂恢复到挤压型稳定状态(图6b).震后足够长时间以后，弧前恢复到震前状态，底部边界摩擦系数均比较小，外部楔形体内部应力状态呈近中性分布，内部楔形体呈挤压型稳定状态(图6c).

外部和内部楔形体底部界面不同摩擦性质可能反映岩石性质的差异.在浅部由于岩石固结程度比较低、孔隙水压比较高等原因，断层性质表现为速度强化.而深部由于更高的温压条件和俯冲脱水过程，岩石固结程度高、孔隙水压比较低，断层从而表现为速度弱化.断层面这种性质的差异性已经被比较广泛的认可，例如Bilek和Lay(2002)指出断层面由浅到深孕震性质这种差异性.

俯冲带生震带位置是地学研究的重要基本问题，对地震灾害性评估具有重要的作用.基于实验室岩石含速率与状态的摩擦性质分析，生震带浅部边界由100～150 ℃岩石温度控制，其深部边界由350～400 ℃温度控制(Hyndman and Wang, 1993; Oleskevich et al., 1999; Moore and Saffer, 2001).在这两个温度范围之外，断层面摩擦性质为速度强化，表现为蠕滑.然而对于缺少地表热流观测值的俯冲带，难以获取其热结构参数，此外地表热流较难以测量.动态库仑楔形体理论提供了一个较方便可靠的办法约束生震带浅部边界，即外部和内部楔形体的交汇处.

Wang等(2019)通过对比东北日本弧前地震震源机制解(例如，Hasegawa et al., 2012; Nakamura et al., 2016)发现，弧前应力在2011年Mw9日本地震前总体呈挤压状态，但是地震后呈拉张状态而产生正断层地震.这些应力变化的总体趋势和图6的结果一致.需要指出的是，本文中的解析解假设理想弹塑性楔形体、均一的楔形体介质和底部摩擦边界，而实际增生楔具有高度不均一性.因此实际应力状态比本文中的结果复杂.基于本文介绍的动态库仑楔形体理论，Wang等(2019)认为断层面摩擦系数需要很小(～0.032)才能产生弧前这种应力状态的地震前后改变.

Ranero 和 Sallarès(2004)基于层析成像数据认为纳斯卡板块在北部智利俯冲时，其上地幔顶部约20 km厚的岩石圈可能含有～17%的蛇纹石，表明可能含有2.5wt%的水.这些含水矿物伴随着俯冲温压条件的改变而产生脱水(Moore and Vrolijk, 1992; Hyndman and Davis, 1992; Davis et al., 2006).脱水反应导致流体可能沿俯冲通道(von Huene et al., 2004)或者沿上覆板块断裂系(Ranero et al., 2008)运移到浅部.更多的弧前洋底流体观测数据有助于我们了解孔隙水压比在地震周期的变化规律，利用动态库仑楔形体理论从而可以更好的理解俯冲带孕震机制和动力学过程.

4 结论

基于理想弹塑性楔形体材料的应力函数解析解(23)式以简洁的形式描述了楔形体在重力和底部静态摩擦共同作用下的内部应力状态.该解析解不仅能描述楔形体处于稳定状态的应力分布，而且能够描述楔形体处于临界破裂状态的应力.经典临界楔形体理论应力解析解从而成为(23)式的子集.

基于应力函数解(23)式提出的动态库仑楔形体理论认为弧前几何形状和构造形变特征的差异性可能反映了俯冲断层面上摩擦性质的不同.弧前海沟附近地表坡度比较陡，地震反射剖面显示复杂的永久变形(外部楔形体).而更远离海沟部分则地表坡度比较平缓，地震波反射体呈水平分布，通常存在未受强烈构造活动扰动的沉积盆地(内部楔形体).动态库仑楔形体理论认为内部楔形体底部为生震带，楔形体在地震周期主要产生弹性形变.而外部楔形体底部摩擦性质为速度强化，地震的时候断层面摩擦系数增加，同时地震的挤压导致外部楔形体孔隙流体压力比升高.更强的断层面摩擦性质和更弱的楔形体材料共同作用导致外部楔形体可能达到挤压型破裂并且产生永久变形.地震以后内部和外部楔形体均逐渐恢复到震前稳定状态.

致谢谨以此文纪念北京大学地质学系王仁教授诞辰100周年.本文主要内容来自于作者在加拿大维多利亚大学博士学习期间发表的研究成果，相关工作和作者博士导师王克林教授(Kelin WANG)合作完成.感谢徐世庆老师、韩鹏老师和另外两位匿名审稿人提出的有益建议帮助完善本论文.