机车齿轮箱齿根裂纹故障解调方法研究
2022-02-23刘新厂陈春俊
刘新厂,陈春俊
(1. 成都工业学院汽车与交通学院,四川 成都 644000; 2. 西南交通大学机械工程学院,四川 成都 610031)
0 引 言
齿轮箱传动系统将电机的扭矩传递给轮对驱动列车运行,是机车的重要组成部分[1-4]。齿轮箱传动系统工作条件十分恶劣,不仅受到传递载荷、轮轨冲击载荷的联合影响,而且还要适应轮对、构架之间复杂的相对运动。在列车运营条件下,齿轮箱传动系统一旦发生故障,故障就会快速发展和蔓延,若不及时发现故障并采取相应措施,会导致齿轮箱的轴承燃烧、齿轮断裂、箱体破坏、动力传递中断以及车毁人亡等重特大事故的发生,严重危及行车安全。因此,齿轮箱传动系统的故障检测与诊断研究是保证列车安全运行的关键。
当齿轮箱传动系统中的齿轮出现故障的情况下,采集到的机械系统振动信号一般会出现调幅以及调频现象,通过解调方法将调制信息提取出来是齿轮传动系统故障诊断的有效方法。国内外学者,在信号解调方面做了大量研究。1982年,国外学者Randall[5]采用高通绝对值解调方法对齿轮箱故障进行监测与诊断。McFadden[6]采用希尔伯特包络解调方法对含有疲劳裂纹故障信息的机械系统振动信号进行处理,很好地提取了信号中所含有的故障信息。1996年,Ma等[7]为了更好地检测齿轮缺陷,提出了一种基于模型的解调方法,该方法可以提取齿轮振动信号中所包含的信息。2001年,Wang[8]提出了一种利用共振解调技术对齿轮齿面裂纹进行早期检测的方案。该方法,首先运用同步信号平均值法去除规则的齿轮啮合谐波,生成残余信号。然后,通过共振解调技术对残差信号解调。最后,利用一些统计量对齿轮是否存在故障进行诊断。2005年,Smith[9]提出了一种新的分解方法:局部均值分解法对调幅和调频信号进行解调处理。2010年,Liang等[10]提出了一种与参数无关但易于实现的旋转机械故障检测技术Teager能量算子解调法,运用该方法对具有调制现象的机械系统振动信号进行处理,实现了对信号的幅值以及频率的解调,成功地对系统故障进行检测。同年,Cheng等[11]针对齿轮振动信号在升、降速的过程中的调制特性,提出了一种基于广义解调时频分析和包络阶次谱技术相结合的故障诊断方法,并将其应用于齿轮振动信号的瞬态分析中。2015年,Jin等[12]采用循环自相关方法对含有调制现象的齿轮箱振动信号进行解调处理取得了较好的效果。2017年,An等[13]提出了一种基于变分模态分解和包络分析的齿轮故障诊断方法。首先,运用变分模式分解法将复杂的信号分解成几个稳定的分量;然后,采用包络解调法对得到的各分量进行了分析。以上分析方法针对的对象以纯旋转为主,然而机车齿轮箱传动系统除了具有自身旋转还要适应车体与构架之间的相对运行,运动更为复杂,所以选择一种适合机车齿轮箱传动系统的解调方法十分必要。
本文对齿轮箱含齿根裂纹情况下,机车各个部件的动态特性进行分析研究的基础上,针对齿轮系统含有齿根裂纹故障情况下采集到的信号会有调制现象的问题进行了解调方法的对比研究。针对机车部件振动信号中的调制现象,运用希尔伯特包络解调方法、复Morlet小波包络解调方法、复Morlet小波簇包络解调方法、复Morlet小波簇带通滤波器及其包络解调法对电机信号进行解调处理,并且对这几种解调方法效果进行对比研究。
1 动力学模型的建立
1.1 含有齿轮箱传动系统的机车轨道耦合垂向动力学模型
含有齿轮传动系统的机车轨道耦合垂向动力学模型来源于参考文献[14]。此动力学模型由机车子系统以及轨道子系统组成。机车子系统包含1个车体、2个构架、4个轮对、4个电机以及4个齿轮传动系统。车体与构架之间通过二系悬挂系统连接;构架轮与对之间通过一系悬挂系统连接;齿轮箱的一端与构架连接,另外一端与轮对连接。机车子系统的各个组成部分具有点头以及垂向振动两个自由度。轨道子系统由钢轨、轨枕、道床、路基组成,它们之间通过弹簧阻尼元件连接。钢轨被视为一个无限长的Euler梁,它与轨枕之间通过弹簧阻尼元件连接。Liang M[10]给出了道床的建模方法,在这个模型当中相邻轨道板之间加入了剪切刚度以及剪切阻尼。轨道子系统的各个组成部分只具有垂直方向的一个自由度。齿轮传动系统由电机、小齿轮、大齿轮组成。电机的转子通过扭簧阻尼元件与小齿轮连接,小齿轮通过啮合力带动齿轮旋转,大齿轮安装在轮对上。齿轮传动系统的各个组成部分只有自身旋转一个自由度。
由于机车被视为一个多刚体系统,所以系统的微分方程可以通过运用D’Alembert准则建立。模型中车辆轨道耦合垂向动力学方程详见文献[14]。
1.2 齿根裂纹损伤动力学建模
齿轮传动的过程中,齿根部位受到弯曲应力的反复作用。齿轮运行一段时间后,齿根部位出现疲劳裂纹。当含有齿根裂纹的轮齿进入啮合时,轮齿的啮合刚度发生变化。Yang等[15]提出采用能量法计算齿轮时变啮合刚度。计算过程中假定齿轮啮合系统的总能量由3部分组成:弯曲势能Ub、赫兹能Uh以及径向压缩变形能Ua。Tian[16]在文献[15]的基础上对该模型进行了改进,考虑了齿轮的剪切变形能Us。
Tian等[17]研究表明:当齿轮根部产生裂纹时,赫兹刚度以及轴向压缩刚度保持不变,只有弯曲刚度以及剪切刚度发生变化。含齿根裂纹情况下齿轮副啮合刚度求解具体方法参照参考文献[17]。
2 含齿根裂纹情况下机车各部件的动态特性
本文通过仿真获得齿轮箱传动系统不考虑齿根裂纹情况下以及考虑齿轮箱传动系统含有齿根裂纹情况下机车各个部件的振动信号,并且对这些信号分析得到车体各个部件的振动特性。含齿根裂纹情况下机车轨道耦合动力学模型参考文献[18]建立。齿轮传动系统参数如表1所示,车辆轨道耦合垂向动力学系统参数详见文献[18]。仿真过程中齿根裂纹长度为q=9 mm。将刚度数值代入动力学模型,采用文献[19]提出的快速积分方法求解系统动态响应。
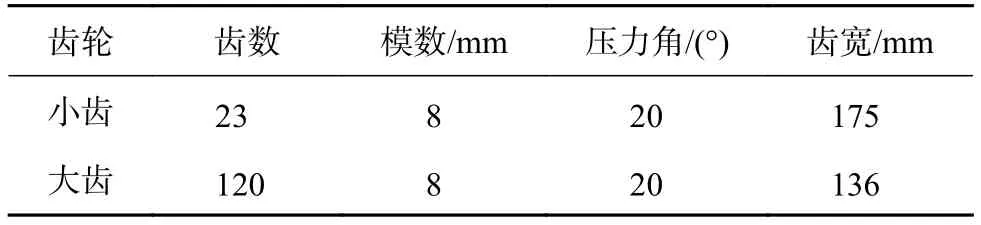
表1 齿轮传动系统主要参数
图1(a)、图1(b)分别为含有健康齿轮传动系统但是不含轨道随机不平顺时,车体振动加速度的时域图以及频谱图。图2(a)、图2(b)分别为含有齿根故障但是不含有轨道随机不平顺情况下,车体振动加速度的时域图以及频谱图。通过图1(a)与图2(a)的对比可以发现,当齿轮箱传动系统具有齿根裂纹故障,车体振动加速度数据数值会相应增加。通过图1(b)与图2(b)的对比可以发现,当齿轮箱传动系统具有齿根裂纹故障,车体振动加速度的频谱图中会出现小齿轮的转频以及倍频成分(fm为齿轮啮合频率,fp为小齿轮故障频率)。
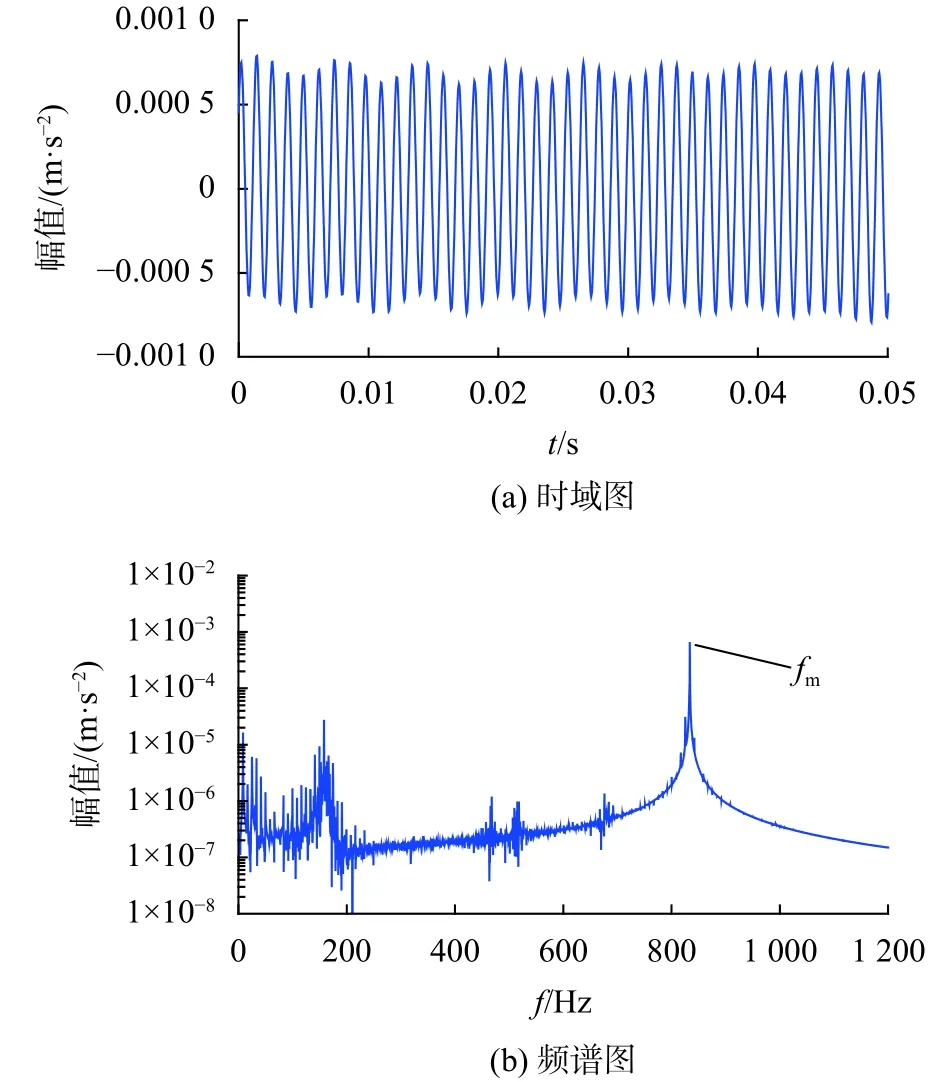
图1 不含齿根故障情况下车体振动加速度的时域图以及频谱图
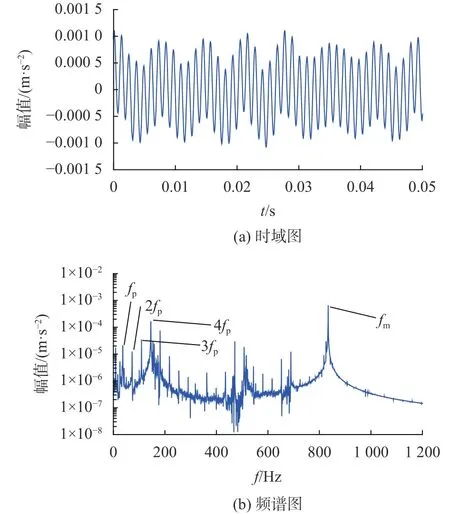
图2 含齿根故障情况下车体振动加速度时域图以及频谱图
图3(a)、(b)分别为含有健康齿轮传动系统但是不含轨道随机不平顺情况下,构架振动加速度的时域图以及频谱图。图4(a)、(b)分别为含有齿根故障但是不含有轨道随机不平顺情况下,构架振动加速度的时域图以及频谱图。通过图3(a)与图4(a)的对比可以发现,当齿轮传动系统具有齿根裂纹故障的情况下,构架振动加速度数值会相应增加。通过图3(b)与图4(b)的对比可以发现,当齿轮传动系统具有齿根裂纹故障的情况下,电机振动加速度的频谱图中会出现小齿轮的转频以及倍频成分。
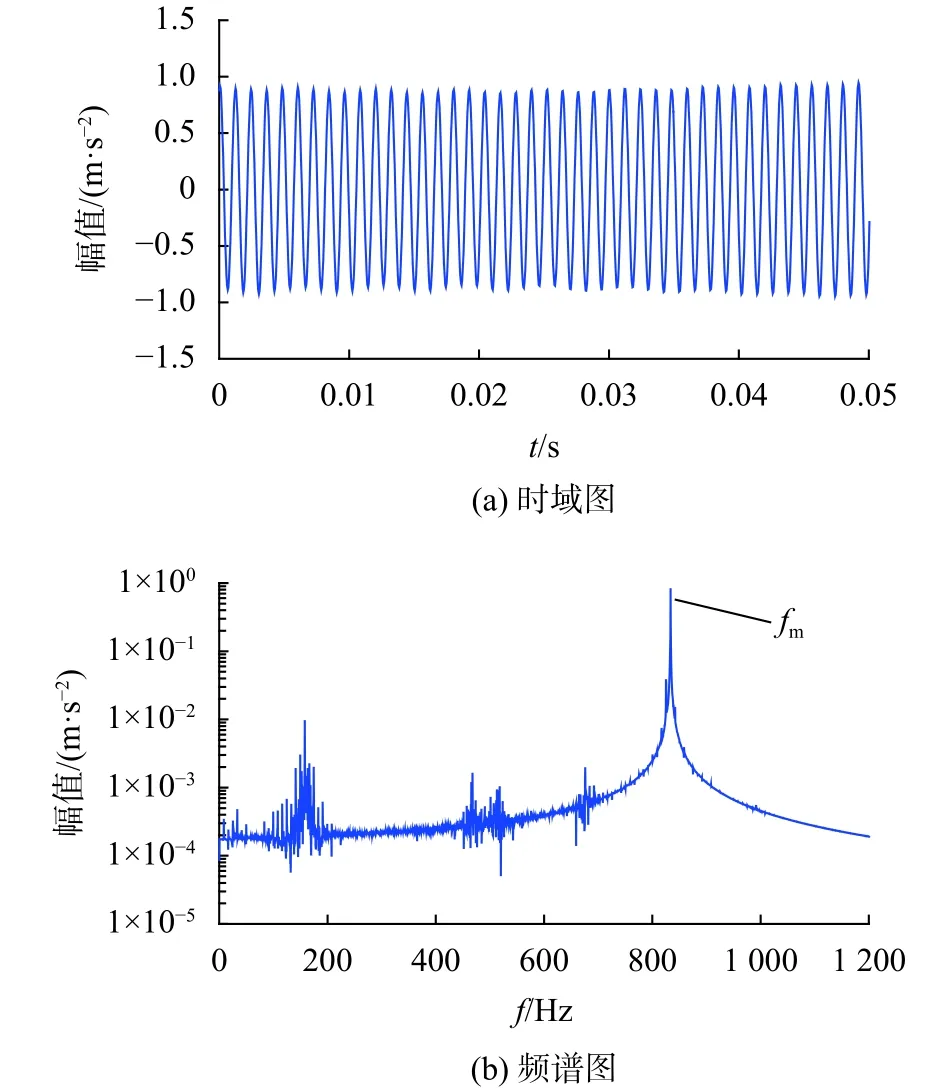
图3 不含齿根故障情况下构架振动加速度时域图/频谱图
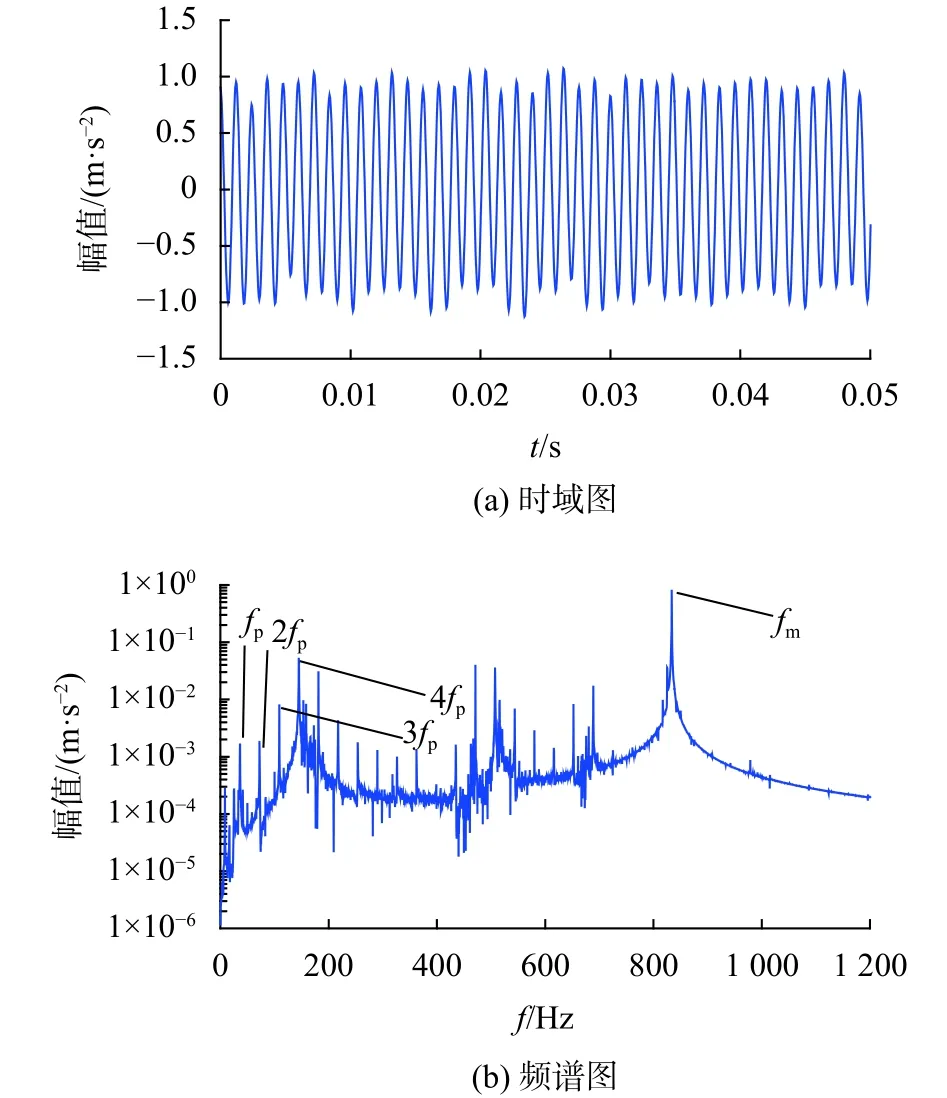
图4 含齿根故障情况下构架振动加速度的时域图、频谱图
图5(a)、图5(b)分别为含有健康齿轮传动系统但是不含轨道随机不平顺情况下,电机振动加速度的时域图以及频谱图。图6(a)、(b)分别为含有齿根故障但是不含有轨道随机不平顺情况下,电机振动加速度的时域图以及频谱图。通过图5(a)与图6(a)的对比可以发现,当齿轮传动系统具有齿根裂纹故障的情况下,电机振动加速度数值会相应地增加。通过图5(b)与图6(b)的对比可以发现,当齿轮传动系统具有齿根裂纹故障的情况下,电机振动加速度的频谱图中会出现小齿轮的转频以及倍频成分。图6(b)中出现了fm+2fp频率成分,说明采集到的电机振动加速度中存在调制现象。
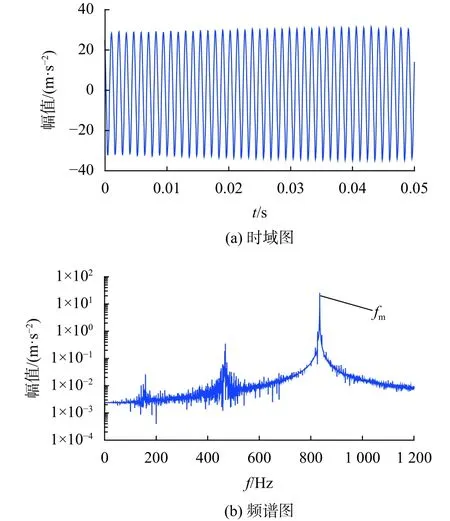
图5 不含齿根故障情况下电机振动加速度的时域图以及频谱图
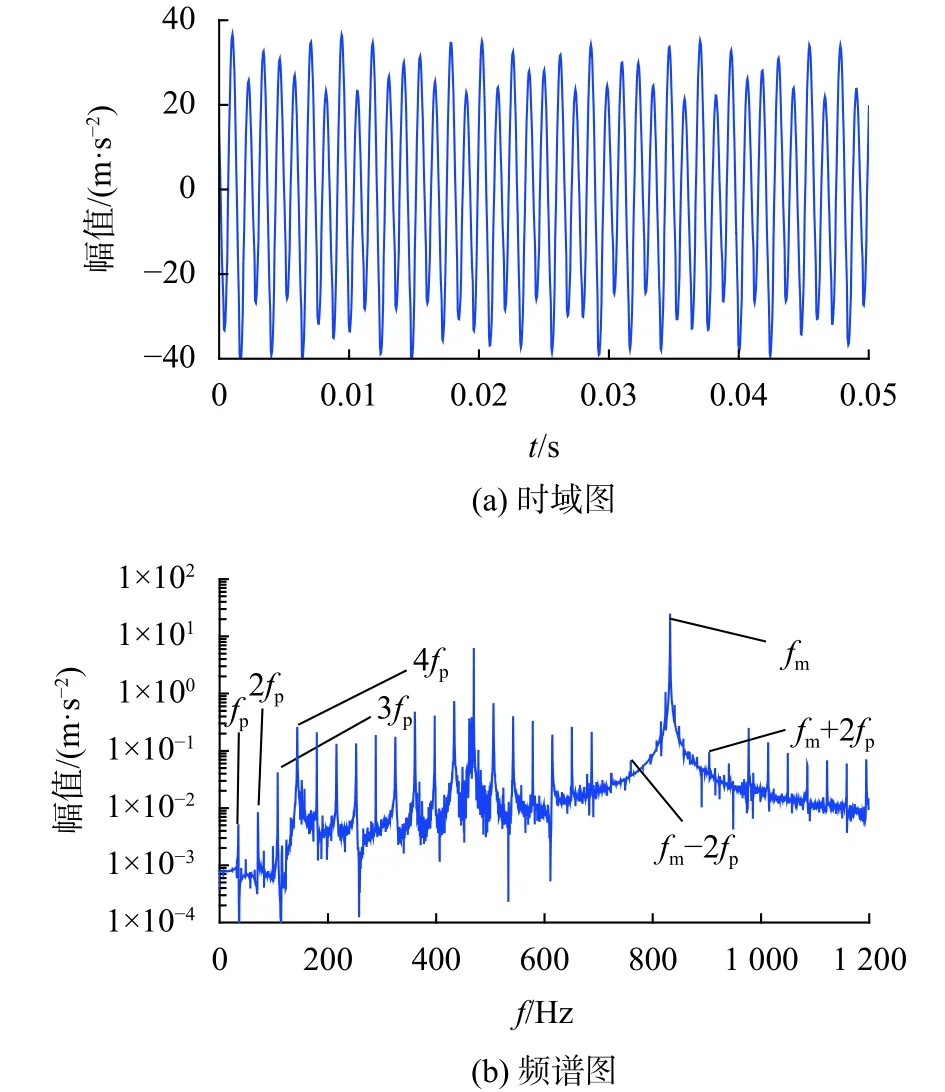
图6 含齿根故障情况下电机振动加速度的时域图、频谱图
图7(a)、图7(b)分别为含有健康齿轮传动系统但是不含轨道随机不平顺情况下,轮对振动加速度的时域图以及频谱图。图8(a)、图8(b)分别为含齿根裂纹故障(传动系统小齿轮具有齿根裂纹)但是不含有轨道随机不平顺情况下,轮对振动加速度的时域图以及频谱图。通过图7(a)、图8(a)的对比可以发现,当齿轮传动系统具有齿根裂纹故障的情况下,轮对振动加速度数值会相应增加。通过图7(b)、图8(b)的对比可以发现,当齿轮传动系统具有齿根裂纹故障的情况下,轮对振动加速度的频谱图中会出现小齿轮的转频以及倍频成分。图8(b)中出现了fm+2fp频率成分,说明采集到的轮对振动加速度中存在调制现象。

图7 不含齿根故障情况下轮对振动加速度时域图、频谱图
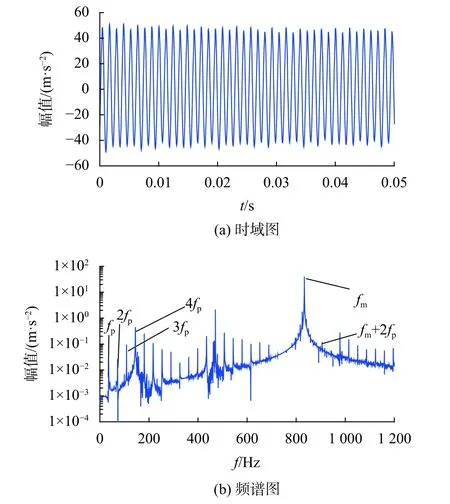
图8 含齿根故障情况下轮对振动加速度时域图、频谱图
通过以上数据分析可以看出当齿轮传动系统含有齿根裂纹故障情况下,车体、构架、电机、轮对的振动加速度信号中都会出现故障频率以及倍频成分。电机与轮对的时域以及频域信号的变化更明显,并且故障频率处信号的幅值远大于车体以及构架信号在故障频率处的幅值,所以由此看来越靠近齿轮箱传动系统的部件越能反映齿轮箱齿根裂纹故障。
同时,当齿轮传动系统存在齿根裂纹的情况下,电机以及轮对的频谱图中出现了fm+2fp频率成分,说明采集到的振动加速度信号中存在调制现象,以上结论与文献[18]基本相同。
3 齿轮箱齿根裂纹故障解调方法分析
通过第二节的分析知道齿轮箱齿轮含有齿根裂纹情况下采集到的机车各个部件的振动信号中会产生调制现象,所以选取有效的解调方法是实现齿轮箱齿根裂纹故障诊断的重要途径。本节通过希尔伯特包络解调方法、解析小波包络解调方法、复Morlet小波簇的包络解调方法以及复Morlet小波簇梳状滤波器的包络解调方法对信号进行分析,并且对这几种解调方法效果进行对比研究。
通过第二节的含齿轮传动系统的机车垂向动力学模型仿真得到含有机车齿轮齿根裂纹故障情况下的机车电机振动加速度信号。仿真过程中列车运行速度为 100 km/h,采样频率为 20 kHz,轨道垂向随机不平顺激励采用美国六级轨道谱。图9为基于Hilbert包络解调方法得到的电机振动加速度的时域图以及频谱图,通过图9可以看出通过Hilbert包络解调方法得到的电机振动信号的频谱图中可以找到齿轮故障频率,但是信号故障频率不突出。
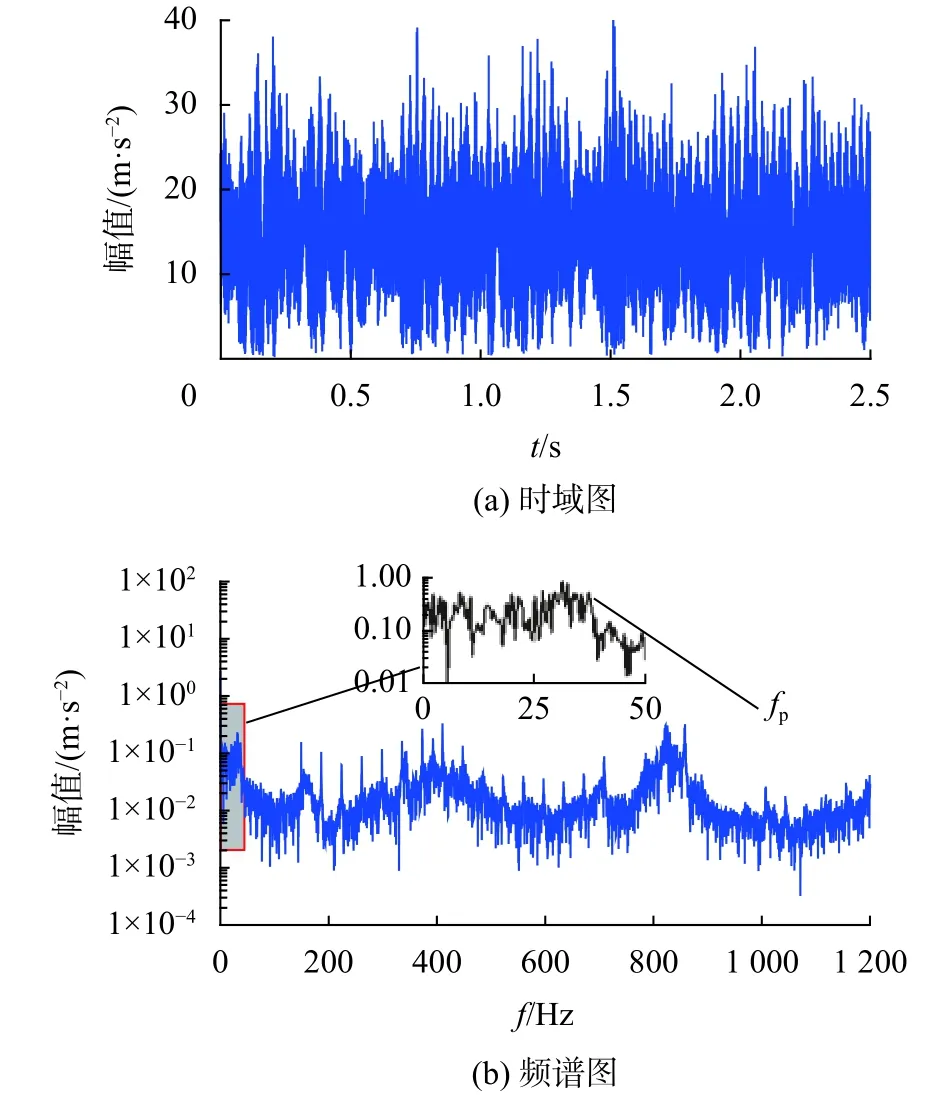
图9 基于Hilbert得到的电机振动加速度的时域图、频谱图
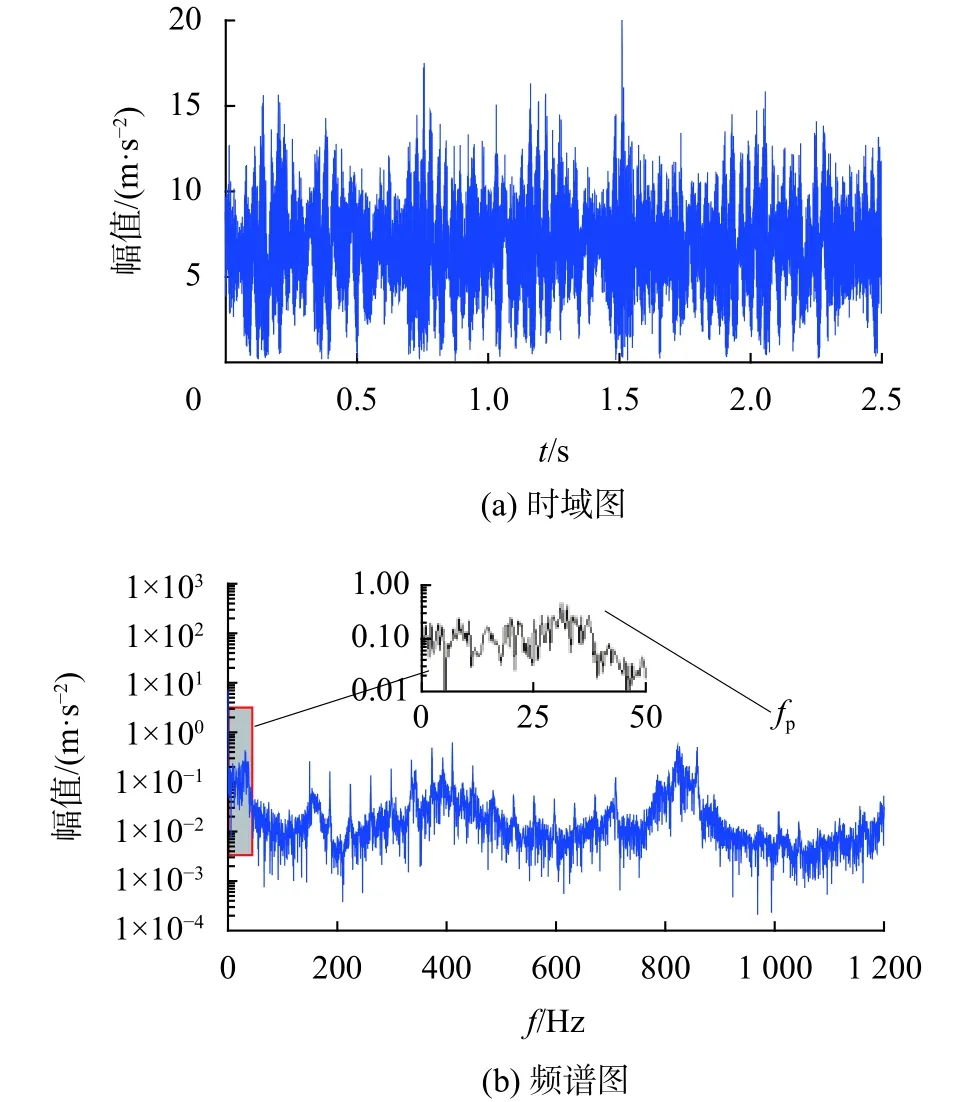
图10 基于复Morlet小波得到的电机振动加速度时域图、频谱图
图10为基于复Morlet小波包络解调方法得到的电机振动加速度的时域图以及频谱图,图11为基于复Morlet小波簇包络解调方法得到的电机振动加速度的时域图以及频谱图。图12基于复Morlet小波簇的梳状滤波器及包络解调方法得到的电机振动加速度的时域图以及频谱图。通过图10、图11、图12的频谱图对比可以发现通过这几种方法都可以将信号中的调试成分进行解调处理,但是受到噪声的影响解调效果都不明显。通过图12得到的解调信号的时域图与其他几种方法得到的时域图的对比可以看出,信号中含有明显的冲击成分,并且通过计算得到冲击点之间的时间间隔与小齿轮旋转所用时间相同。通过图12得到的解调信号的频谱图与其他几种方法得到的频谱图的对比可以发现,此种方法解调得到的信号中能清楚看到所包含的故障频率成分。表2为通过各种解调方法得到的信号信噪比的数值,通过复Morlet小波梳状滤波器解调方法得到的信号中故障频率成分信噪比最高。
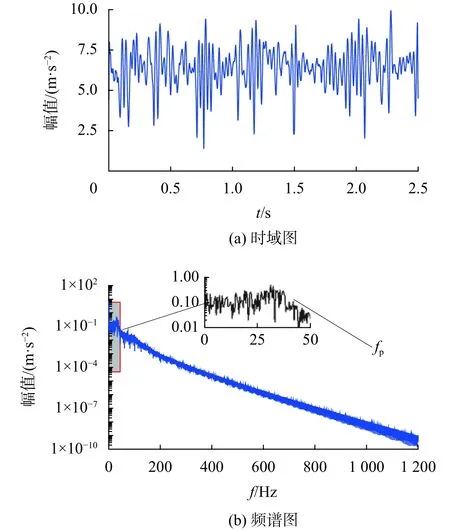
图11 复Morlet小波簇的电机振动加速度的时域图、频谱图

表2 解调方法信噪比对比
4 结束语
本文将齿根裂纹故障引入到含有齿轮箱传动系统的机车轨道耦合垂向动力学模型中,分析含有齿根裂纹故障时机车动态特性,针对齿轮系统含有齿根裂纹故障情况下采集到的信号会有调制现象进行了解调方法对比研究。通过分析得到以下结论:
1) 当齿根裂纹出现故障的时候,齿轮的转动频率会在频谱图上出现。其中,电机以及车轮垂向振动加速度的频谱图上会具有较为明显的齿轮的啮合频率与转频的差值,说明含有齿根裂纹故障情况下采集到的机车各个部件的信号中存在调制现象。
2) 通过几种常用的信号解调方法对含有齿根裂纹故障下采集到的电机振动信号进行分析发现基于复Morlet小波簇的梳状滤波器在对电机振动信号进行包络解调的过程中能够针对信号中的主要频率成分进行提取,从而达到消除信号中的噪声的干扰的目的,使得解调得到的信号包络更加明显。
