腿足式救援机器人运动控制算法分析与展望

刘雪飞，张文昌，吴 航，陈 炜*

（1.天津理工大学机械工程学院天津市先进机电系统设计与智能控制重点实验室，天津 300382；2.天津理工大学机械工程学院机电工程国家级实验室教学示范中心，天津 300382；3.军事科学院系统工程研究院卫勤保障技术研究所，天津 300161）

0 引言

灾害救援环境复杂多变，传统的人力方式给救援人员带来巨大的生理和心理压力，采用智能机器人手段代替人力方式是未来重要的发展方向。救援机器人按照运动机构形式分为轮式、履带式和腿足式。然而，在复杂地形环境中，轮式和履带式救援机器人的适应能力和灵活性较低，很难完成复杂的现场救援任务。而腿足式救援机器人结构灵活、适应能力强，可以提高救援现场的作业效率。腿足式救援机器人主要分为仿生串联和并联结构形式[1]，运动特点是足端与地面的接触不连续，可以选择合适的立足点，躲避障碍，但也导致了其运动失衡的问题。因此，应采用高效合理的控制算法实现腿足式救援机器人的稳定运动，提高侦察和救援效率，保障后送伤员安全。高效合理的控制算法将成为腿足式救援机器人处理应急事件的重要技术手段。本文以腿足式救援机器人的模型控制算法、仿生控制算法和机器学习控制算法为主要内容进行综述，重点介绍这3种控制算法的研究现状、优缺点和发展趋势。

1 研究现状

稳定的运动状态是腿足式机器人需要解决的首要问题，学者们也针对此问题展开了深入研究，并且取得了较大的研究进展。起初是围绕机器人的结构特点展开研究，总结出了模型控制算法，其中包括稳态判据控制算法、虚拟模型控制算法（virtual model control，VMC）、弹簧倒立摆控制算法（spring-loaded inverted pendulum，SLIP）[2]；随着各种学科的不断发展，仿生控制算法被提出，将计算机科学和生物学有效地结合在一起[3]，使腿足式机器人可以灵活运动，达到了仿生效果；仅有灵活的运动能力并不能应对复杂环境中的突发情况，因此，将机器学习控制算法作为腿足式机器人的高层控制，以应对复杂环境中的突发情况。3种控制算法的发展及应用，丰富了腿足式机器人的运动模式，提高了机器人的执行效率。

1.1 模型控制算法

模型控制算法是腿足式机器人的基本控制算法，即底层控制算法。首先，根据机器人物理样机的尺寸和质量参数确定运动学或动力学模型；其次，建立机器人足部运动参数和力/力矩的关系方程式；最后，求解模型中的参数，得到驱动系统的实际控制量。根据模型控制算法的应用方式，分为稳态判据控制算法、虚拟模型控制算法和弹簧倒立摆控制算法。

其中，稳态判据控制算法是模型控制算法中较为经典的算法，由Vukobratovic等[3]提出，虚拟模型控制算法和弹簧倒立摆控制算法均由稳态判据控制算法演化而来，保证机器人质心总是落在支撑足端构成的多边形内部，实现机器人稳定运动。随着计算机控制技术的发展，McGhee等[4-5]结合稳态判据控制算法研制了世界上首台采用计算机控制的腿足式机器人Phony Pony，精确描述了腿足式救援机器人的静态步态数学模型和腿部的摆动顺序，提高了机器人在平整地形上的流畅度和稳定性，但是稳态判据控制算法只适用于平整地形环境，对复杂地形的适应性较低，而虚拟模型控制算法和弹簧倒立摆控制算法的提出，弥补了稳态判据控制算法对复杂地形适应性低的不足。

1.1.1 稳态判据控制算法

腿足式救援机器人在救援现场需要稳定的运动状态，需要保证机器人质心的垂直投影必须在支撑足端所组成的多边形内部，将质心垂直投影与支撑足端所形成的多边形的位置关系作为腿足式机器人稳定运动的判据，称其为稳定性判据。目前，国内外应用较为广泛的稳定性判据包括零力矩点判据（zero moment point，ZMP）[6-9]、能量稳定裕度判据（energy stability margin，ESM）[10]和动态稳定裕度判据（dynamic stability margin，DSM）[11]。

稳态判据控制算法的共同特点是规划好机器人足端运动轨迹和质心的位移，简化机器人控制，明确机器人运动规律，但是降低了机器人的流畅度和运动速度。早在1995年就有学者关注了这个问题，普渡大学机器人实验室的学者Pack等[12]将动态稳定裕度判据和A*搜索法结合，使机器人可以选择合理的立足点，提高了运动的稳定性。A*搜索法如图1所示。但是机器人在运动时卡顿严重，流畅度较低，执行效率严重下降，产生这种问题是因为没考虑到能量消耗。日本东京工业大学福岛实验室在此问题的基础上提出方向归一化能量稳定裕度判据算法[13]，此算法可以提高机器人的外部干扰能力和流畅性。波士顿动力公司在研究腿足式机器人初期，为使机器人站立稳定，大量应用此算法在机器人身上。但是应用此算法的前提是低速无扰动，因此稳态判据控制算法更适用于对运动速度要求低的场合。

上海交通大学高峰教授的团队基于前述理论研发了2款腿足式救援机器人，第一款为带腰仿生六足机器人，如图2（a）所示[14]。在这款机器人的控制方面应用了能量稳定裕度判据算法，提高了机器人的稳定性并改善了能耗问题，可用于野外环境探测与作业，代替救援人员携带检测设备进入事故发生地点，探测灾后环境，搬运救灾物资等。第二款为“六爪章鱼”机器人，如图2（b）所示，团队同样将能量稳定裕度判据算法应用在机器人的控制方面，使移动自如的“六足”具有良好的复杂环境适应能力，可在核辐射、水下和火灾等极端环境下完成搬运、搜索、探测和救援作业等任务[15]。这2款腿足式救援机器人融合了上述理论，在实际的应用和测试中都展现出令人满意的效果。

图1 A＊搜索法[12]

图2 救援机器人

1.1.2 虚拟模型控制算法

虚拟模型控制算法由Pratt等[16]在《虚拟模型控制：两足行走的直观方法》一文中首先提出，主要原理是在机器人外部连接虚拟的弹簧和阻尼等，算出机器人机构平衡时的虚拟力，再通过功能关系求出机器人的关节力。Pratt等[16]在Spring Turkey机器人样机上应用了虚拟模型控制算法，在实验过程中展现出满意的结果，然而虚拟模型的盲目应用也会导致控制算法失效。意大利理工学院高级机器人实验室Winkler团队将虚拟模型控制算法应用于HyQ四足机器人上[17]，并在模型上新增加了向前反馈扭矩传感器，提高了机器人系统的精度和高度顺从性，避免了侧向冲击的干扰。

国内在此方面也开展了研究。山东大学的刘斌等[18]提出一种基于虚拟模型控制算法的腿足式机器人缓冲策略，在Scalf-2机器人上得到了验证，如图3所示，通过假想的弹簧阻尼系统驱动机器人按照预期的轨迹运动，为足式机器人的抗冲击能力提供了控制基础，增加了机器人运动的稳定性。Scalf-2为腿足式机器人，质量为120 kg，可承担质量75 kg，全速运动时速度达到3 km/h，应用缓冲策略后可以在冰雪环境和复杂山地环境下运送救援物资，减轻救援人员负担。北京理工大学和北京交通大学在前述基础上，提出了基于虚拟模型控制的动态平衡控制和抗干扰控制算法[19]，并在如图4所示的四足机器人上得到验证，增强了四足机器人的鲁棒性、地形适应性和动态平衡性。但是，无论是虚拟模型控制算法还是传统动力学控制算法都需要建立精确的力学模型，如果机器人本体结构及其所应用的环境复杂，其模型也随之复杂，给控制算法的研究工作增添了挑战性。

图3 山东大学研制的Scalf-2机器人[18]

图4 北京理工大学和北京交通大学研制的四足机器人[19]

1.1.3 弹簧倒立摆控制算法

弹簧倒立摆控制算法的灵感来源于对足式动物运动的观察，此算法是由Geyer等[20]最先提出，分别应用到人体运动和腿足式机器人运动控制方面，弹簧倒立摆模型如图5所示。被广泛熟知的波士顿动力公司的大狗机器人[21]除采用液压缸和柴油发动机等硬件作为驱动部分外，在腿部控制方面结合了弹簧倒立摆控制算法的思想，被成功地应用到救援物资的运输中。但是此控制算法的数学模型是非线性模型，不存在解析解，为求解带来了困难。为此，英国比尔肯特大学的研究员在原模型的基础上引入阻尼，如图6所示，推导出了一个高精度的近似解析解模型[22]，并且引入了额外的校正来补偿由重力引起的非对阵角动量影响，经测试表明该方法在阻尼显著的情况下产生的平均误差低于2%，明显提高了近似解析解的精度。

图5 弹簧倒立摆模型[20]

目前国内对弹簧倒立摆控制算法的研究也逐渐成熟，华中科技大学在考虑到三维环境中受到外部扰动的情形后，提出了弹簧-负载倒立摆三维动态平衡控制算法[23]，提升了原算法的抗扰动性，扩展了弹簧-倒立摆控制算法的应用范围。哈尔滨工业大学将此算法应用到了双足机器人模型上，并在此基础上研究了线性倒立摆模型预测控制算法[24]，使足式机器人驱动执行力增强、负载刚度提高，因此在大型起重设备无法进入救援现场时，可应用此款足式机器人完成救援现场的起重工作，缓解救援人员的操作压力。哈尔滨工业大学提出的线性倒立摆模型概念，主要优势在于使动力学模型线性化，求解出解析解；考虑了偏航角动量问题，减缓了机器人足端与地面之间的碰撞。

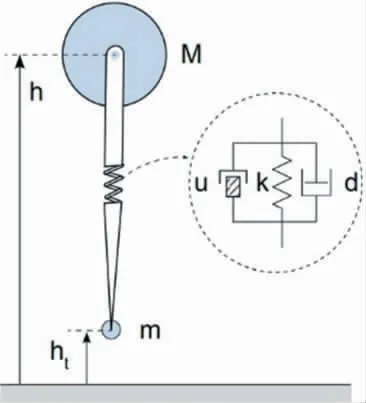
图6 弹簧-阻尼倒立摆模型[22]

1.2 仿生控制算法

如果只在接收简单的、低维度的输入信号的情况下，控制系统能够产生高维度、有节奏的输出信号，将为控制腿足式机器人带来很大方便。学者们也从生物神经学方面得到了灵感，提出仿生控制的概念，即有脊椎和无脊椎动物体内存在一种可以产生节奏性信号的神经回路，可以在不接收节律信号输入的情况下产生节律性的神经活动。学者们从此种仿生角度探寻出新的腿足式机器人控制方法，其中广为关注的是基于中枢模式发生器的控制算法（central pattern generators，CPG）[25]，此类算法基本分为两类[26]：一类是以Matsuoka控制算法为代表的神经元算法模型，另一类是以Hopf控制算法为代表的非线性振荡算法模型。

Venkataraman[27]首次把CPG应用到六足机器人步态生成和控制方面，成功实现了机器人腿部节律运动的控制，由于首次研究只关注了节律信号的生成，所以运动的生成比较简单。为生成自适应性运动，CPG产生的节律信号应该更具有合适的频率、相位，而日本科学家Matsuoka[28]于1985年提出的Matsuoka控制算法初步解决了上述问题，这也使CPG首次模型化，为后续CPG的改进和其他CPG数学模型的提出提供了依据。Matsuoka控制算法在腿足式机器人控制方面具有2个特点：第一，可以产生稳定的节奏模式，系统在受到瞬态扰动后可以迅速恢复其正常的节律；第二，Matsuoka控制算法通常具有一些控制参数（如驱动信号），允许调节运动，如速度和方向甚至步态类型。因此，正确调节算法参数，使高级别控制器直接产生多维命令，简化了控制命令。然而，此类Matsuoka控制算法参数繁多，增加了调参难度，限制了所需形状节律信号的产生，降低了在复杂环境中运动的适应性。

为解决这一问题，中南大学王勇团队提出了一个新的Matsuoka控制算法改进框架[29]，将模型的重心输出转化成一个标准化的极限环，并将极限环与机器人反馈相结合，进行神经网络学习生成所需信号。通过机器人自适应全方位行走控制实验，表明该改进的算法框架明显提高了机器人行走的适应性，如图7所示。虽然此研究改善了Matsuoka控制算法信号的生成问题，但增加了控制过程步骤，同时增加了机器人硬件匹配的难度。除Matsuoka控制算法外，还有Hopf控制算法、Van der Pol控制算法和Toda-Rayleigh控制算法[30-32]，这3种算法的优势在于理论参数简洁，实用性强。波兰罗兹理工大学分别采用这3种控制算法研究了八足机器人的腿部运动和受力问题[如图8（a）所示]，并提出一种新的正弦控制算法模型，通过机器人能量的消耗方式评估4种中枢模式发生器；经仿真实验发现相频特性影响Hopf控制算法、Van der Pol控制算法和Toda-Rayleigh控制算法的振幅和频率，而对新提出的正弦控制算法只影响振荡的频率[33]。新提出的算法结合八足机器人本身小巧灵活的特点，在救援前期的侦察工作中能发挥重要作用，为工作人员提供现场实际情况，提高救援效率。

图7 机器人适应性行走试验[29]

构建完整的CPG网络是灵活控制足式机器人不可或缺的步骤，也是亟待解决的实际问题。哈尔滨工业大学从模拟生物CPG网络出发，构建了一种较为完善的多层CPG网络，使CPG整体简单、结构清晰[34]，并验证了多层CPG网络的可行性。浙江大学在研究多足式机器人控制时采用了这种CPG网络，并在此基础上提出一种基于强化学习的模态控制器自整定法，解决了大部分CPG应用的局部性和CPG的不完整性[35]，并将自整定法应用到六足机器人上，如图8（b）所示，其中由18个伺服电动机作为驱动元件，3个电动机为一组，分布在6条三自由度的串联腿上，使机器人有较高的自由度，同时，配备了外部相机来跟踪机器人并提供反馈信息，使其在崎岖不平的地形中可以像蜘蛛一样顺畅通过，为现场救援、地形勘测带来了福音。但是，强耦合性是CPG不可避免的问题，调整腿部相位时容易产生较大影响。由此可见，CPG更适合于对周围环境变化较小的机器人控制系统。

图8 多足机器人模型

1.3 机器学习控制算法

机器学习是人工智能的核心，在腿足式机器人领域的主要应用是对机器人进行模拟控制，不断学习和积累经验，提高腿足式机器人的运动性能。目前，机器学习各种网络模型均采用了BP（back propagation）算法，即误差后向传播算法[36]，最早是由Werbos[37]在1974年的博士论文中首次论证，但当时没有引起较大的重视；1982年加州理工学院的物理学家Hopfield[38]提出著名的Hopfield模型理论，解决了旅行商[39]问题，推动了人工智能的快速发展；1986年在Rumelhart等[40]的努力下，BP算法被再次优化，并广泛应用于升级网络的训练中。如今，机器学习控制算法开发均采用了1986年经典的BP算法思想，但是由于此算法在执行过程中采用弱监督学习的方式，缺乏认知性控制，所以存在不易学习、容易陷入决策困难等问题[41-43]。

为解决上述问题，加州大学Peng等[43]提出一种由数据驱动的机器学习控制算法，用于训练模型的控制策略，通过对Atlas机器人的行走、奔跑、后空翻和侧踢等复杂动作的实验，展现出此算法可以提高机器人的整体性，如图9所示。机器学习使机器人模型从零开始学习，无形中增加了机器人的控制难度和研制周期，而且基于机器学习算法的腿足式机器人的研究主要局限于仿真环境。如果机器学习算法能够实现无模型化，那么在一系列具有挑战性的控制任务中都能提高救援机器人的决策性和感知性，而且能解决容易陷入决策困难的问题。如前所述，对于腿足式机器人的学习控制局限于仿真环境，搭建的仿真环境虽然很严格，但是都与真实的环境有一定的差异，致使在仿真环境中开发的学习策略在真实环境下可应用的概率很小。Google的Tan等[44]实现了学习策略从仿真环境到现实环境的迁移，如图10所示，解决了腿足式机器人控制方法从仿真环境到真实环境的转移问题。Lee等[45]在仿真环境中直接学习真实环境中的运动，这一思路大大提高了学习速度。

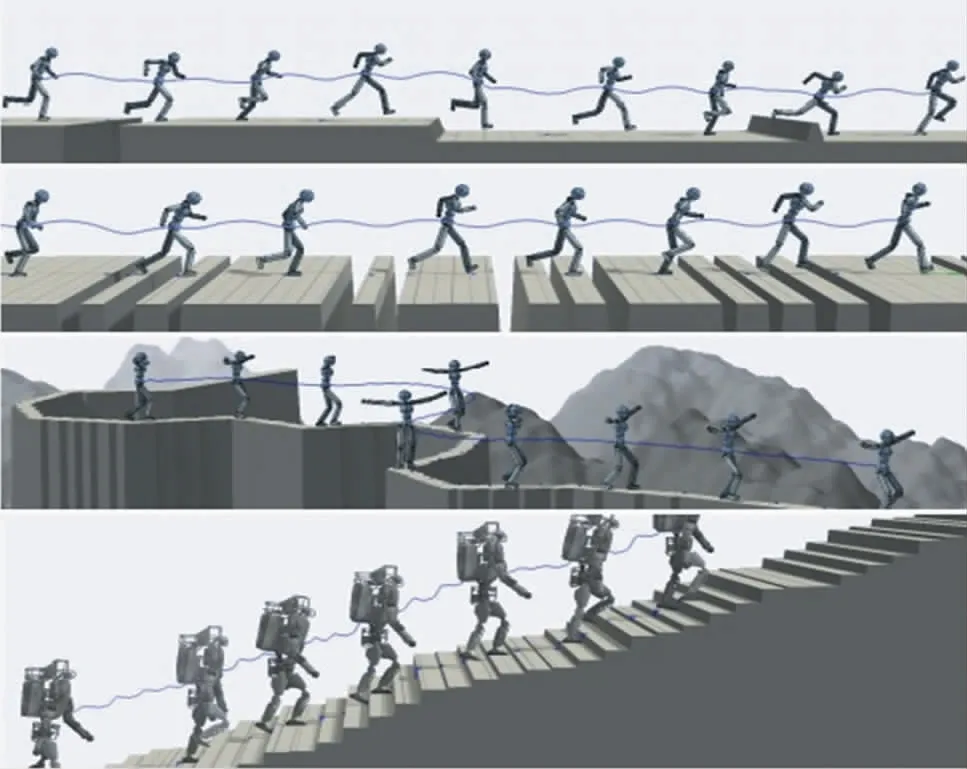
图9 模型技能训练实验[43]

图10 算法迁移试验[44]

国内对机器学习控制算法的理论研究较少，更多体现在此控制算法的实际应用中。目前，腾讯公布了在腿足式机器人研究方面的新进展：四足移动机器人Jamoca，如图11（a）所示[46]。Jamoca本体质量70 kg，长1 m、宽0.5 m、站高0.75 m。腾讯Robotics X实验室在机器人本体之上，基于机器学习控制技术，为Jamoca打造了一个能应对复杂环境的智能大脑，这个大脑使Jamoca能行走、小跑和跳跃，并赋予了它自主定位和避障的能力。除腾讯外，国内宇树科技研发的莱卡狗[47]，如图11（b）所示，是国内首个腿足式机器人，质量仅22 kg，但其自行研发的电动机系统能输出高达18 kW的瞬时功率，功率密度比一般跑车高将近1倍，这是莱卡狗强大动态性能的基础。另外，莱卡狗可以完全摆脱外部供电，自带电池一次充电可以支持2～3 h的行走。今后，在救援方面可以应用这2款机器人完成地形勘探和信息搜索工作，提高侦察救援工作效率。

图11 基于机器学习的四足机器人

2 控制算法优缺点分析

腿足式机器人经过十几年的发展，在结构上逐渐完善，焕然一新的结构也层出不穷，与这些结构相匹配的控制算法也层见叠出，不断优化和改进。这些控制算法在腿足式机器人控制方面已经取得了一定成效，但是在面对不同环境的情况下也是各有利弊，基本集中在算法的复杂程度、计算时长、所需数据量的多少以及对机器人的控制效果等方面。下面将针对3种算法的特点分别阐述优缺点，详见表1。

表1 各算法特点对比

模型控制算法是腿足式机器人研究中的基本控制算法，应用较为广泛。模型控制算法优势如下：（1）具有精确的模型，可以很好地控制机器人的运动规律；（2）参数都有精确的物理含义，可以实现精确的实时控制；（3）可控性强，易于理解。模型控制算法的不足之处就在于它需要具体模型，建模过程困难，求解烦琐，计算量大，对研究的硬件设备有较高的要求，而且模型多为复杂的微分方程，求解结果不唯一，有时模型可能无解，这些都给建立控制系统带来了麻烦。所以模型控制算法更适用于机构模型简单的机器人。

仿生控制算法的提出开启了机器人仿生控制的大门，这种控制算法的优点如下：（1）不需要精确的模型；（2）只需产生低维信号，就可以对机器人关节进行控制。此算法也有不足之处，仿生模型产生信号是无量纲的，没有具体的物理意义，与机器人结构的关联性较弱，需要对信号进行后期处理，而且仿生模型具有强耦合性，容易引起腿部控制的干扰。仿生控制算法更适用于模型复杂和模型所处环境变化不大的控制系统。

机器学习控制算法是目前研究的热点，是人工智能的核心问题，也是未来腿足式机器人深化研究的大方向。机器学习控制算法的优点如下：（1）对于模型中难以确定的参数，可以通过机器人的学习进行调整；（2）机器学习控制算法可以使机器人不断学习和积累经验，做出相对灵活的动作；（3）机器人可以通过机器学习控制算法，从仿真环境中直接学习，在真实环境中实现大部分人类很难做到的高难度动作，提高机器人整体的运动性能。但是这些都需要大量的数据存储空间和强大的配套硬件设备，对机器人训练需要海量数据，大大增加了计算时间，而且对于多维度、结构复杂的腿足式机器人，机器学习控制算法很难保证控制的实时性。所以机器学习控制算法主要应用在对实时性要求不高的机器人运动规划场合。

3 展望

目前在移动式机器人控制领域，腿足式救援机器人控制已经取得了一些进展，现有的救援机器人技术也在不断完善，为了能更好地将腿足式救援机器人投入到救援工作中，多控制算法融合、控制算法高效规划等关键性技术应该是未来腿足式机器人控制技术发展的侧重点。

3.1 多控制算法融合

由于灾后或战后救援，腿足式救援机器人需要处理一些复杂的任务，单一运动控制算法难以满足任务对机器人运动精度的要求。此外，尽管不同控制算法在机器人不同运动控制问题上均有一些优势，但也存在一定程度的不足。因此，通过结合多种运动控制算法，可以有效整合各自算法的优势，弥补各自的不足，从而为腿足式救援机器人运动控制精度提供保障，国内外目前也都在考虑这方面的技术问题。

3.2 控制算法高效规划

近几年，腿足式救援机器人的运动控制算法规划方法主要停留在先运动后应对的思想上，即在运动过程中，机器人会按照预先规定的轨迹运动，随后根据感知反馈信息对突发情况进行反应和适应。当机器人在复杂地形运动时，一种更加高效的方法是直接根据当前环境预先生成相应的运动轨迹，再利用前述的控制策略应对运动过程中的偏差和地形不确定性，即先规划后应对的思想。因此，需要对腿足式救援机器人基于地形的全身运动规划算法进行研究。

4 结语

随着腿足式机器人技术的不断成熟，腿足式救援机器人控制算法得到了快速发展，并取得了一定成果，但各国的腿足式救援机器人控制算法与全智能化控制算法的理念相比还存在一定的距离，主要体现在运动算法的规划方面。为了更好地实现侦察救援和机器人的强自主适应性，腿足式救援机器人控制算法应朝着根据当前环境实时规划运动轨迹的方向发展，并结合5G技术提高信息传输效率以应对地形的不确定性。未来，随着控制算法不断优化，智能技术不断更新，腿足式救援机器人会被广泛应用到侦察救援等复杂的工作领域。