边缘计算中多设备多任务的能耗均衡优化算法
2022-02-23武继刚姚棉阳
庞 源,武继刚,陈 龙,姚棉阳
广东工业大学 计算机学院,广州510006
近年来,随着科学技术水平的提高,增强现实、虚拟现实、实时游戏等时延敏感型应用迅速发展。此类应用的发展通常需要高性能机器支持。然而,随着移动设备的普及,用户倾向于在移动设备上完成各项任务。当用户希望在移动设备上完成各项任务,包括时延敏感型应用,就需要移动设备拥有足够强大的计算能力和续航能力。但是,由于移动设备的便携性,其体积通常不会很大,其计算能力和续航能力无法得到保证。为此,欧洲电信标准协会引入了移动边缘计算(mobile edge computing,MEC)来解决这个问题。近几年来,MEC 发展迅速,在视频内容传输、无人驾驶汽车等领域都有着重要的应用。随着物联网和第五代通信技术发展迅速,互联网中数据交换量不断增大。据思科白皮书估计,到2022 年,移动设备的人均拥有数量将达到1.5 台,移动设备将占全球IP 总流量的20%。当这些移动设备产生的数据都传输到核心云服务器并由其完成时,势必导致网络的拥塞。但MEC 的应用解决了这些问题。
MEC 通过协助完成移动设备的任务,可以减少移动设备完成这些任务的能耗和时延。然而,由于移动设备的功率有限,在节约能耗的同时提高其计算能力成为了一项挑战。现今的研究通常关注利用边缘服务器或远程云,以提高移动设备的计算能力,比如利用边缘服务器和云服务器来最小化总能耗或最小化任务完成时间。但是目前的这些研究大都没有涉及多移动设备共存计算任务卸载场景下,移动设备能耗均衡保障问题。
多设备多任务的能耗均衡问题是最小化多个设备的最大能耗问题。假设有一个名为的边缘服务器和两个分别名为、的移动设备。为了简化,假设移动设备、均存在两个任务,这两个任务均需要在两个时间周期内完成。为简化描述,假设边缘服务器和移动设备在每个时间周期只能运行一个任务。此外,任务交付到边缘服务器执行时,所产生的能耗代价更低。如果将中的两个子任务都交付给,则无法再使用边缘服务器,这导致设备的能耗显著高于设备,显然这是不均衡的。因此,为了达到能耗均衡,需要重新设计任务调度策略。
据了解,与本文研究最相似的文献为文献[12]和文献[13]。其中文献[12]的结构也是三层结构,同时考虑了任务的依赖关系,但其目标是最小化总能耗,没有考虑移动设备能耗的均衡问题。并且该文章的结构由端边云三者组成,也没有考虑到使用中继设备来优化系统。而文献[13]的结构为多个原设备和一个由边缘服务器集成的无线访问接入点(wireless access point,AP)组成,研究的是两个用户下最小化加权能耗和。但该文献也并没有使用中继设备,且该文献中的任务是可以被随意划分的,任务之间不考虑依赖关系。
因此为了改进现有的工作,综合上述文章,本文在原有的结构中去除了传输能耗更大的云服务器,加入了中继设备节点作为任务的中转节点,构成了一个由移动设备、中继设备和边缘服务器组成的三层结构。本文的贡献点如下:
(1)基于上述结构设计了一种满足任务依赖的多设备多任务能耗均衡贪心算法MMG(min-max greedy algorithm)。较之现存的最小能耗算法,MMG 算法在具有任务依赖关系的多设备多任务能耗均衡问题上具有更有效的表现。
(2)将能耗均衡问题转化为最小化最大能耗问题,并且设计了总能耗优化算法以及随机算法来与MMG 算法进行对比。
(3)为了验证MMG 算法的优越性,进行了大量的对比实验。实验结果证明,MMG 算法的平均性能在能耗均衡方面可进一步提升66.59%。
1 相关工作
在MEC 的研究上,大部分的团队集中于研究如何充分地利用服务器的资源以提高移动设备的性能。其目标一般分为两种:节约能耗成本和减少任务完成时间。
在节约能耗成本上,文献[14]设计了一个动态计算卸载算法和一个对应的在线卸载算法来解决动态计算卸载问题和节省移动设备能耗。文献[15]提出了一种调度算法来分配无线带宽,使所有用户的总成本最小化。文献[16]提出了两种卸载策略,以最小化延迟约束下的能耗。文献[17]提出了一种边缘云架构,并设计了贪心算法来最小化移动设备的总能耗。文献[18]设计了一种结合“0-1”编程和联盟博弈并通过在移动用户之间共享计算结果的分布式算法来最小化移动设备的总能耗。文献[19]研究的是在一个由远程云和异构本地处理器组成的体系结构中,在时间约束下最小化应用程序总执行成本问题。文献[20]提出了一种分布式线性松弛启发式算法和贪婪启发式算法来最小化移动用户的总能耗。文献[21]考虑的是能耗问题和敏感型任务的调度策略问题,并设计了一种分布式动态卸载和资源调度策略,目标是最小化移动设备能耗,但没有考虑设备间的能耗均衡问题。上述的这些文章都没有充分考虑任务完成时间的问题,也没有考虑利用中继设备的协作作用来更好地优化移动设备的能耗。
在降低任务完成时间上,文献[22]通过利用马尔可夫决策方法,提出了一种高效的一维搜索算法,使每个计算任务的平均延迟最小化。在多用户多任务问题上,文献[23]设计了集中式分布式贪心最大调度算法,解决了多用户多任务计算卸载问题,但文章没有考虑任务依赖关系。文献[24]提出了一种“边缘-云”协作的“依赖-感知”卸载方案,并设计了两种算法,解决的是在任务依赖约束和给定预算的情况下最小化设备任务完成时间。文献[25]假设边缘服务器的资源无限大,研究不同移动用户随机到达的异构延迟敏感计算任务环境下,使移动用户在任何给定的计算卸载策略下的总时延最小问题,并将该问题建模成一个动态优先队列,同时设计了一种优先传输调度策略来解决。然而上述文章也都没有考虑使用中继设备。
除能耗和任务完成时间外,也有一些研究致力于解决边缘计算所遇到的其他难解问题。文献[26]利用博弈论设计了一种分布式计算卸载算法,研究了多信道无线干扰环境下的多用户卸载问题。文献[27]利用进化博弈策略来研究动态环境下的多用户计算卸载问题。文献[28]利用无人机的移动性来解决边缘服务器的低移动性问题。
2 模型
本章将会先介绍本文系统的模型。本文所使用到的符号及其含义如表1 所示。

表1 本文所用符号Table 1 Notations of this paper
2.1 系统模型
如图1 所示,系统是一个具有三层架构的移动边缘计算模型。系统的顶层位于一个具有计算能力的边缘服务器上,而这个服务器一般位于基站或远程访问点。系统的中间层为中继设备,它们只负责任务传输但不负责任务的执行。系统底层是移动设备,每个移动设备都有一个正在运行的应用程序,每个应用程序由多个具有任务依赖关系的子任务组成。

图1 系统模型Fig.1 System model
移动设备通过无线连接的方式与中继设备进行通信,如Wi-Fi 等。中继设备也通过无线连接与边缘服务器通信。模型中存在多个移动设备,用集合M={,,…,m}表示,其中是移动设备的数量。此外,模型中的中继设备用集合H={,,…,h}表示,其中是中继设备的数量。对于每一个移动设备,都包含个有依赖关系的子任务,用N={,,…, n}表示。
以下,将详细介绍本文的通信模型和计算模型。
2.2 无线通信模型
无线通信存在于移动设备和中继设备以及中继设备和边缘服务器之间。根据香农公式,从第个移动设备到第个中继设备之间的上行数据速率可以表示为:

类似地,第个中继设备与边缘服务器之间的上行数据速率为:



其中,d为节点与之间的欧式距离,为路径损失分量,且,∈{M ⋃H⋃{}}。
2.3 计算模型
当中的在移动设备本地执行时,其执行时间可以表示为:

其中,W是完成第个移动设备中的第个子任务所需要的工作量大小,f是第个移动设备的CPU 时钟周期频率,单位为cycle/s,对应的能耗可以表示为:

其中,ρ为取决于移动设备架构的一个正常数。如果第个移动设备中的第个子任务被卸载到第个中继设备时,此阶段的传输时间可以表示为:

其中,D为第个移动设备的第个子任务的数据量大小。这个过程的能耗可以表示为:

如果第个移动设备中的第个子任务从第个中继设备被卸载到边缘服务器,此过程的传输时间可以表示为:

对应的能耗为:

在边缘服务器上完成第个移动设备的第个子任务的计算时间为:

其中,f为的CPU 时钟周期频率,单位为cycle/s。
因此,完成第个移动设备的第个子任务的能耗为:

2.4 任务依赖性
本节定义了子任务之间的依赖关系。子任务的完成时间分为以下几部分。










因此,第个移动设备完成所有子任务所需要的时间为:

综上所述,第个移动设备的总能量消耗可以表示为:

2.5 问题定义
本节将给出最小化最大能耗问题的公式化定义。最小化最大能耗问题描述如下:

其中,为给定的第个移动设备完成所有子任务的预算时间。式(20)是对第个移动设备的完成时间的约束。式(21)和式(22)是子任务的依赖性约束,确保第个移动设备的第个子任务只能在其所有前驱子任务完成后才能开始执行。式(23)表示第个移动设备的第个子任务只能在本地执行或者在边缘服务器执行。
据现有的研究可知,最小化最大能耗问题是一个找寻调度策略的优化问题,可以规约为文献[29]中的最小化最大时间问题,而该文献将最小化最大时间问题规约为NP-hard 整数规划问题。因此,最小化最大能耗问题为NP-hard。
3 算法设计与分析
本章对提出的MMG 算法进行详细描述。
本文根据子任务的数量将划分为几个部分,并且每一层的每个子任务都应该在划分完成之后的区间结束。对于每个子任务,根据时间和能耗条件确定计算模式。然后,对于每个子任务,通过最小-最大算法来获得分配方案。此外,再判断分配方案是否满足时间限制。
在以上分析的基础上,首先,通过计算获得不同子任务在本地计算、迁移到边缘服务器计算的能耗,并形成一个能耗矩阵。对于每一个移动设备源节点,都随机分配一个中继设备节点。假设是源节点到中继的最大能耗,找到并将所有中继设置为“unused”,当中继设备被占用时设置为“used”。获取分配策略。逐个判断最大能耗所分配的中继设备节点之外是否有其他中继设备节点可用。若可用,则更换中继设备节点,确定新的(调整能耗使得分配策略所得的总能耗在尽量小的情况下能耗差更小)。若未找到其他可用中继设备节点,则开始判断分配策略是否满足时间约束,若不满足,则重新分配策略;若满足,则获得可行分配策略。
设定移动设备的数量为,每个移动设备的子任务数量为,中继设备的数量为。算法的总时间复杂度为(+)。
首先,本文提出的算法分三层嵌套循环来计算时间消耗和能量消耗,其时间复杂度为()。然后,分析了最小-最大函数的时间复杂度。每次迭代的复杂度为(),每次迭代最多有对,因此最小-最大的总时间复杂度为()。在时间检查方面,这是一个只有一层循环的sum 函数,包括两层嵌套的While 循环,每个While 循环不超过次,因此其时间复杂度为()。此外,第二步是在不同的子任务层下执行的,因此第二步的总时间复杂度为()。该算法的总时间复杂度为(+)。
任意移动边缘计算结构的二部图都可以转化为能量消耗矩阵。将和分别表示为一个任意小的正常数和子任务数,则该贪心算法的近似比可以达到(1+)。
在定理1 中,分析得到算法的时间复杂度为(+),其最大的迭代次数为。对于一个子任务而言,根据式(7)、式(9),分别令其传输能量比为和;根据式(5),令其计算能量比为。每个“设备-中继”对的能耗可以表示为E=min(σ+γ, ψ)。“源-中继”的最大和有效最小能耗分别设为和。则有:

其中

因此,每个“设备-中继”对的能量消耗上界为。设=/,其中为每个“设备-中继”对最大能耗平均调整的步长,是迭代的最大次数,则有=/。设()为最小化每个“设备-中继”对的最大能耗的最优解,其中对应的最优策略。设′为贪心算法中每个“设备-中继”对的最大能耗,则有()≤(′)。又=/,则有=。因此,是其中一个移动设备能耗调整的上界。据此,则有:根据式(24)和0 <<(),有:



本文所提出的贪心算法伪代码如下所示:
Min-max greedy algorithm(MMG)
输入:工作量大小,数据量大小,时间约束。
输出:分配策略。

Min-max algorithm
输入:子任务数量的级别,能量消耗矩阵。
输出:分配策略。
1.for(,) in listdo
2.检查中继节点的可用性
3.if(,) is availability then
4.将源节点的对移除
5.将(,)对分配给源节点
6.回到第二行来确定一个新的
7.if no pair availability then
8.算法结束
4 性能评估
本章设计了实验来研究所提出的算法的性能。本文利用Matlab r2016a 进行了大量的实验,并得到了实验结果。
文中将覆盖范围设定为50 m×50 m。默认情况下,子任务、移动设备和中继设备的数量分别设置为4、3和3,实验中的其他参数如表2所示。在整个实验过程中,文章假设计算任务的数据大小、工作量大小在[25 Kbit,1 024 Kbit]范围内遵循正态分布,平均值为512,标准差为256。此外,本文还设计了一个总能耗优化算法(total energy consumption minimization algorithm,TECM)的实验对比算法。
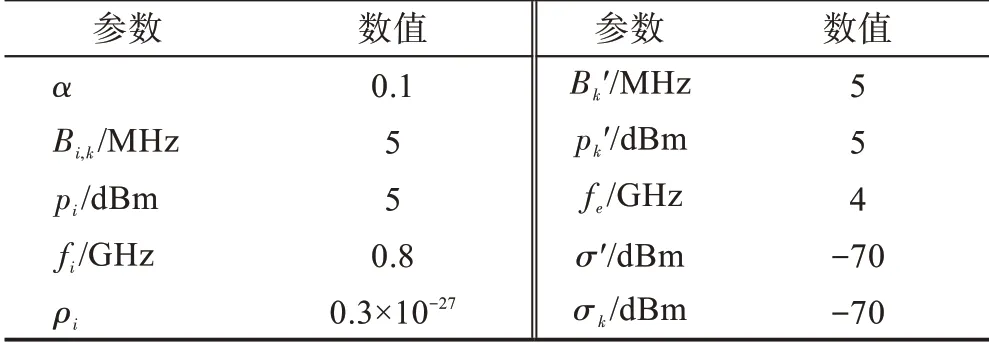
表2 实验参数Table 2 Experimental parameters
在实验1 中,文章研究了路径损耗分量与子任务最大能量消耗之间关系的变化。图2(a)描述了子任务的最大能量消耗随着路径损耗分量的增加而增加。从式(1)、(2)、(3)、(6)、(8)中得出,子任务的最大能量消耗与路径损耗分量成正比,这解释了实验图2 中的曲线形状。实验表明,当移动设备的传输功率分别为5 dBm 和6 dBm 时,MMG 算法在最小化子任务的最大能耗方面的性能平均比随机算法提升66.59%和61.87%,接近蛮力算法得到的最优解。图2(b)基于图2(a)的结果,结果表明,当移动设备的最小传输功率分别为5 dBm 和6 dBm 时,MMG 算法的近似比分别为1.096 9 和1.098 4。

图2 实验1Fig.2 The first experiment
实验2 研究了子任务在时间约束变化下的最大能量消耗。在图3(a)和图3(b)中,移动设备的最小传输功率为5 dBm。结果表明,贪心算法的性能优于总能耗优化算法和随机算法。

图3 实验2Fig.3 The second experiment
最后,在路径损耗分量为0.1 的情况下,文章观察了子任务的最大能量消耗随任务层数的变化。如图4(a)所示,随着任务数量的增加,每个子任务的完成时间相应地减少,从而导致任务需要在更短的时间内执行。这导致完成任务所需的能量消耗增加。但是MMG 算法在最小子任务的最大能耗的性能上明显优于TECM 算法和随机算法。如图4(b)所示,随着子任务数的增加,子任务的最大能量消耗增加,当移动设备的传输功率分别为5 dBm 和6 dBm 时,MMG 的近似比分别为1.353 7、1.353 8。

图4 实验3Fig.4 The third experiment
5 结束语
本文研究了多移动设备多任务中的能耗均衡问题,这个问题是NP-hard。文章在原有的结构中去除了传输能耗更大的云服务器,加入了中继设备节点作为任务的中转节点,构成了一个由移动设备、中继设备和边缘服务器组成的三层结构。同时本文设计了MMG 算法来求解能耗均衡问题,并通过大量的对比实验证明了MMG 算法的有效性。
