VMD方法在紫金山金铜矿爆破振动信号中的应用

崔年生，夏鹤平，钟添榕，蒋伟，王元䘵

（福建省新华都工程有限责任公司，福建 厦门 361000）

随着国内工程建设和开发项目数量的快速提升，爆破技术在工程领域中发挥着越来越重要的作用，在爆破作业应有越来越广泛的同时，也显露了许多现实问题，其中爆破振动的危害效应尤为突出。当爆破振动效应达到一定强度时，容易对周围建筑设施和人员造成安全隐患和财产损失，有效地控制爆破振动的危害效应一直都是国内外工程爆破领域的重大研究课题。由于爆破地震波在岩土介质中的传播及其引起的地面振动是一个复杂的过程，影响它的因素有很多，如炸药属性﹑炸药数量﹑装药方式﹑炸药堵塞质量﹑爆心位置﹑起爆网络﹑地震波传播介质以及一些现场的其他因素的影响。同时，它又与爆区附近的地质条件﹑建筑物本身的材料特性以及施工质量等因素有关。因此，各国科研工作者分别从爆破振动危害效应﹑振动的监测方法﹑振动信号的分析处理﹑爆破振动对建筑物的破坏判据以及控制降低振动危害等方面做出了大量的研究，并取得了一定的理论进步及应用成果。然而，由于爆破振动信号本身就是不稳定随机信号，加上实际地质情况的复杂多变，以上的综合因素使爆破振动信号的随机性变得难以预测。在目前研究中尚未完整的掌握地震波的传播规律，研究爆破振动效应及控制危害仍有很长的路要走。

1 变分模态分解基本理论

变分模态分解（Variational Mode Decomposition，VMD）将信号分解为一系列有限带宽变分模态分量，将信号转移到变分框架内进行分解，通过寻找模型最优解实现信号分解。分解后各个变分模态分量的估计带宽之和最小，各变分模态分量之和等于原始信号，数学公式为：

为了求式（1）（2）的最优解，引入增广拉格朗日将变分约束问题变为变分非约束问题，其表达式如下：

其中，α为二次惩罚因子，λ(t)为拉格朗日乘法算子。

利用交替方向乘子算法解调上式，得到一系列uk和ωk，即为K个模态分量的中心频率和带宽。具体步骤如下：

式中，τ为保真系数；

（4）重复步骤（2）（3）直至（7）满足，最终得到K个变分模态分量：

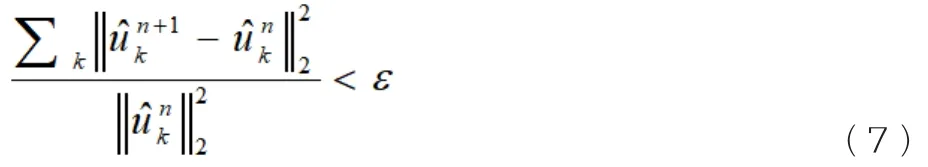
式中，ε为容差。

2 模拟信号分析

为了验证VMD方法的准确性及模态参数识别的有效性和抗噪性，利用EMD﹑VMD方法对仿真信号进行分解。设置仿真信号Signal由Signal1，Signal2和一个随机噪声Signal3组成。

仿真信号的波形及频谱信息如图1所示，在频谱中可得知仿真信号有大量的高频干扰噪声，其优势频段在10～50 Hz和70～100 Hz。分别采用EMD﹑VMD方法对仿真信号进行分解，结果如下：

图1 仿真信号及频谱

采用EMD分解后的结果如图2所示，可看出该信号由EMD方法分解后得到7个IMF分量，其中IMF1代表噪声信号，IMF2和IMF3分别代表两个变频信号，但和初始信号相比，分解后得到的变频信号频带变宽，出现严重的模态重叠的问题，IMF4～IMF7是原始信号中没有的分量，说明原始信号经EMD分解后得到过多的IMF分量，出现模态分裂的问题。综上可知，EMD的分解结果模态分裂，而且噪声的存在影响了分解效果，很难分辨信号中的有用成分。说明EMD分解方法不适合短时非线性信号的分解。

图2 EMD分解结果及频谱

VMD分解效果如图3所示，从图中可以看出，VMD良好的分解出仿真信号中的两条变频信号，分解出的变频信号的频谱光滑，不存在噪声干扰和模态重叠的问题，较好还原了信号中的有用信息，更好地表示出原信号的组成成分，各模态的物理意义更加明显，验证了VMD方法的优越性。

图3 VMD分解结果及频谱

3 应用实例

针对矿山周边典型的被保护居民区建筑物进行振动测试，将测点布置在具有明显破坏特征的地基或墙角位置，以便真实反映爆破作用在建筑物区域产生的质点振动速度，从信号能量层面分析爆破振动对破坏特征明显建筑物的影响。现场共布置3个测点，测点与爆源几何中心的水平距离分别为587.45m﹑590.36m﹑595.43m，测点的高程分别为47.52m﹑48.87m﹑49.35m，高程差与水平距离的差异性小忽略不计。现场监测仪器安装如图4所示。

图4 现场监测点

爆破振动测试采用四川拓普测控科技有限公司生产的一体化爆破测振仪iSV-420，此仪器可一键完成三维速度﹑加速度等振动参数测量，还可通过手机﹑平板﹑PC无线远程控制；设备体型小巧，方便携带，坚固美观，适用于工程爆破振动的现场测量，测量精度为0.5%，测量范围在0.01cm/s～40cm/s（X﹑Y﹑Z三向）之内，低频响应可往下低至0.01Hz。在测点位置用石膏把传感器与地面紧密粘连，以便真实反映基岩受爆破引起的质点振动速度。对爆破振动进行监测﹑记录。典型测点实测波形如图5所示。

图5 现场监测波形图

运用VMD方法对爆区周边居民区爆破振动信号进行分解。图6为监测点信号波形的VMD分解得到的各IMF分量和Res分量。

图6 实测信号VMD分解

随着分解的进行，所得分量的频率逐渐降低，波长波动变长，最后处理得到一个频率很低的Res分量。在地形﹑地质和测点位置相同的条件下，虽然单段最大装药量的不同，但测点距离较大，不同装药量条件下垂直方向的爆破振动峰值速度不同，各测点信号分解后所包含的分量数目相同。随着单段最大装药量的增加，噪声分量减少，振幅也出现增大的现象，但第三次爆破试验测得的峰值振速和第二次无太大差异性，推测可能的原因是前两次爆破振动导致岩体介质出现节理裂隙，对爆破振动的衰减作用增大。图6清晰的彰显了VMD对各分量的分解还原度很高，解决了模态混叠特性，抗噪能力强，IMF1为高斯白噪声。得出的分量结果表明VMD方法模态分解效果好。

采用matlab程序对部分分量信号进行瞬时频率谱计算。图7为各测点振动信号的瞬时频率谱，根据瞬时频率谱可以看出“频率—时间—瞬时能量”的变化特征，测点分量1振动信号能量在频率上的分布以20～60Hz为主，主振频率为40Hz左右，在时间上的分布以0.1～0.7s为主，但0.7s后色标颜色变得不是很明显，说明0.7s后的振动能量以低频信号所携带的能量占比为主。根据图7（b）可以看出，分量2测点的能量在频率上的分布主要为20Hz左右，频率分布具有比较好的稳定性，在时间上以0.3～0.5s和0.7～0.8s两个集中段为主，能量具有过度集中现象，造成此现象的原因可能是没有合理设置延时时间。图7（c）可以看出，分量3能量在频率上的分布以18～30Hz为主，主振频率为20Hz左右，低频能量分布均匀，低频能量对建筑物破坏较大。总体来看，随着段数装药量的增加，瞬时频谱颜色逐渐加深，爆破振动信号能量整体呈放大的趋势，三次爆破试验的信号能量主要分布在0～80Hz范围内，以低频段能量集中为主，能量集中时间段与原始爆破地震波较大幅值对应的时间段相一致，能量最大值出现在峰值振速对应的时间处。

图7 分量瞬时频率谱

根据研究结果来看，在矿山爆破远距离区域，振动信号的主振频带为低频带，基本没有高频带振动信号。分析表明，爆区周边居民区的振动信号大部分能量主要聚集在低频部分，建筑物对爆破振动的响应是在药量﹑岩体节理裂隙﹑爆心距与高程变化等多影响因素作用下综合表征的结果。优化后VMD方法对爆破地震波这类非线性非平稳曲线处理得出的瞬时频率谱图精准并清晰地揭示了时间—频率—能量分布特征。VMD方法可以很好地刻画爆破振动信号的非线性动态变化特征，该方法为爆破振动信号的深入研究提供了一种新的思路。

4 结语

综上所述，本文对变分模态分解方法在爆破工程中的应用进行了详细分析和总结。变分模态分解方法提高了爆破振动信号分解的精度，提高了信号时频分析的准确性，明确了各个分量的物理意义，取得了一定的成果。但从目前来看，在其他爆破振动信号，如隧道爆破﹑拆除爆破中作者还未进行系统的研究，因此要加强该方法在不同种类信号中的适用性研究，进一步促进爆破工程领域的发展。