基于PELT的交通流状态检测与短期预测研究
2022-02-22陈王勇
陈王勇, 胡 尧, 2
( 1. 贵州大学 数学与统计学院, 贵州 贵阳 550025; 2. 公共大数据国家重点实验室, 贵州 贵阳 550025)
0 引言
在很多交通流状态分析研究中,高峰期存在平稳状态都是一个潜在的假设。而近平稳状态的识别对于检测交通活动瓶颈,校准基本图以及量化容量变化的幅度大小具有重要意义。Jin近年的一系列研究中,在运动波理论框架内证明了一般道路网络中平稳状态的存在和稳定性[1-3]。然而,由于不可避免的噪声干扰和随机波动,原始检测数据中不存在严格的平稳状态,因此,在实践中平稳状态只能是近似平稳的。
现有的识别此类近平稳状态的研究通常是由校准基本图的需要所推动的。Del Castillo等[4]提出潜在的近平稳状态持续时间至少4或5 min且标准差小于平均值的15%,基于此准则对速度序列进行目视选择,进一步基于Kendall’s tau检验,提取速度和车辆计数序列中无趋势的近平稳状态。由于上述方法使用目视检查,并且在处理大量数据时耗费时间和人力。因此,需要有效识别近平稳状态的自动方法。最近Yan等[5]基于PELT(Pruned Exact Linear Time)搜索算法的变点检测方法,将交通流时间序列划分为多个可能接近平稳状态的候选间隔,计算每个候选间隔的特征,通过修改Cassidy准则实现了近平稳状态的自动识别过程,但是对数据要求较为苛刻。邬群勇等[6]基于公交车和出租车轨迹数据对城市交通状态进行了精细划分和识别,实现对城市交通状态的分析。本研究在文献[5]的基础上,提出随机化的交通流基本参数,根据不同的速度和密度需求,精细划分交通状态,并结合时间序列方法,运用ADF(Augmented Dickey-Fuller)检验[7]构建交通流近平稳状态检测方法。
在智能交通系统的研究领域中,除了上述交通状态检测研究外,短期交通流预测也是研究的热点之一[8-12]。而非参数回归方法在交通流预测中扮演着重要的角色[13],早期Sun等[14]提出局部线性回归模型应用于短期交通预测,该方法具有一定的时效性,但是对带有异常值的数据不具有鲁棒性。进而Cleveland[15]提出具有鲁棒性的LOESS(Locally Weighted Regression and Smoothing Scatterplot)方法,通过计算和绘制平滑点,大大增强了散点图上的视觉信息。Sun等[16]提出具有鲁棒性的自适应参数的k近邻方法用于短期交通流预测,但交通流历史信息考虑不足。对此,本研究引入局部多项式回归[17],并综合考虑当前的交通流信息以及历史交通流消息,对未来的交通流进行短期预测。基于PELT搜索算法,结合Sigma原则,得到短期断面交通流趋势预测区间。
本研究内容安排如下:首先定义划分交通流状态,接着构建基于PELT搜索算法的交通流变点检测方法以及近平稳状态的检测模型,引入局部多项式回归方法,并与LOESS,k近邻等非参数回归方法进行预测精度的比较,最后以实际交通流数据验证所提方法的有效性。
1 交通流近平稳状态检测模型
1.1 交通流状态
在时空区域Ω={(t,l):t∈T,l∈L}中,交通流率、密度、速度在时刻t位置l处分别记为q(t,l),k(t,l)以及v(t,l),则有如下状态:
定义1若时空域中的流率和密度均与时间无关q(t,l)=q(l),k(t,l)=k(l)或等价地表示为:
(1)
则称该时空区域中的交通流状态是平稳的(stationary state)[5]。
定义2若时空域中的流率和密度均与时间和位置无关q(t,l)=q,k(t,l)=k,或等价地表示为:
(t,l)∈Ω。
(2)
则称该时空区域中的交通流状态是稳定的(steady state)[5]。
在上述的定义中,并没有考虑交通流基本参数的随机特征。在实际中,由于道路交通运行复杂,交通数据更是异构多源,时空性明显,且交通状态是交通运行系统中不同通行能力供需变化的综合体现,故本研究将从统计角度随机意义下去划分交通状态,即将时空区域Ω中的流量Q(t,l)、密度K(t,l) 以及速度V(t,l)均映射到实数域R。在统计意义下,将通行能力记为交通流量条件期望最大值,其基本计算公式如下:
C=max{E[Q(t,l)|V(t,l)]:(t,l)∈Ω},



(4)
式中kj为交通阻塞密度(jam density)。
综上可知,统计意义下定义的自由流、中断和拥堵等交通状态中均存在近平稳状态。本研究旨在研究交通流量参数近似常数下的一种近平稳状态检测以及交通流的短期预测。
1.2 基于PELT搜索算法的交通流变点检测模型
数据预处理:记q1:n=(q1,…,qn)表示观测到的交通流序列,其中n是样本量。采用如下公式对交通流序列进行标准化处理,使其平均值为0,标准差为1。
(5)


为了检测变点数量和位置,构造如下优化问题:
(6)
式中,θ为间隔的损失函数;β为避免过度拟合的惩罚参数[20]。特别地,使用两倍的负对数似然函数来表示损失函数:
(7)

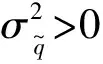
m+1。
(8)
进而得到交通流标准化序列的目标函数:
(9)
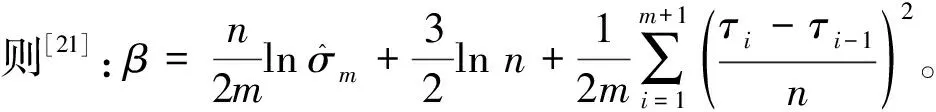
为了求解上述的最优问题和寻找最优的变点位置,采用基于动态规划和剪枝技术的PELP算法得到交通流标准化序列中检测的最优变点位置:
(10)
定理:通过样本标准差重新调整惩罚参数,数据标准化不影响观测序列中检测到的变点数量和位置。
证明:将(5)式代入标准化序列的目标函数(9)式中可得:
(11)
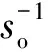
定理表明适当的惩罚参数选择说明式(10)也是交通流观测序列的最优变点位置。
1.3 近平稳状态检测模型

qt=μ+φ1qt-1+…+φpqt-p+εt,i.i.d
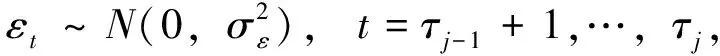
j=1,…,m+1,
(12)
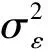
若交通流序列{qt}平稳,则φ1+φ2+…+φp<1;
若交通流序列{qt}非平稳,则φ1+φ2+…+φp=1。
记ρ=φ1+φ2+…+φp-1,则AR(p)过程的ADF检验原假设和备择假设如下:
H0:ρ=0v.s.H1:ρ<0。
(13)
当γ≤γα时,拒绝原假设H0,认为序列{qt}显著平稳,即第j个候选间隔为近平稳状态;
当γ>γα时,接受原假设H0,认为序列{qt}非平稳,即第j个候选间隔为非近平稳状态。
2 交通流短期预测方法
2.1 局部多项式回归
针对交通流序列,除了对交通状态的检测外,还需要根据当前的历史数据对未来的交通流趋势做出判断。本研究采用局部多项式回归[17]对交通流时间序列进行短期预测。该方法是一种基于光滑思想的非参数回归模型,记观测到的一组样本数据为(ti,qi)(i=1,…n),则可建立如下非参数模型:
qi=m(ti)+εi,i=1,…,n,
(14)
式中,m(t)=E(q|t)为q关于t的回归函数,并进一步假定E(εi)=0,Var(εi)=σ2。局部多项式基于加权最小二乘的思想,利用k(k≥1)阶多项式去逼近回归函数。
记Q=(q1,…,qn)T,T(t0)=((ti-t0)j),i=1,…,n,j=0,…,k。设m(t)具有k阶连续导数,对定义域中任一点t0,进行Taylor展开,则在t0的邻域内有:
(15)
式中,αj(t0)=m(j)(t0)/j!(j=0,1,…,k),选择合适的αj(t0)(j=0,1,…,k)使得式(16)达到最小

(16)

记W(t0)=Diag(Kh(t1-t0),…,Kh(tn-t0)),α(t0)=(α0(t0),…,αk(t0))T,则由加权最小二乘方法可得α(t0)的估计值为:
(TT(t0)W(t0)T(t0))-1TT(t0)W(t0)Q。
(17)

(18)
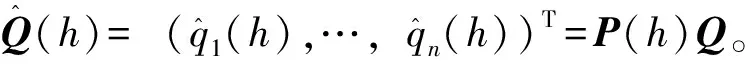
(19)
式中ω(t)为非负的权函数,则最优光滑参数为:
(20)
2.2 模拟和预测比较
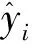
(21)
(22)
为了说明局部多项式回归的有效性,本研究将该方法与LOESS,k近邻等经典的非参数回归方法进行比较。在k近邻回归中,k取值过小会出现过拟合现象,而k取值过大会出现欠拟合现象,为防止过拟合或欠拟合本研究k取3和6。首先通过模拟基准[24]来检测方法的性能,其次基于贵阳市中山西路与瑞金中路交叉口(由南往北方向)2 min断面交通流数据,通过上述回归方法分别进行短期预测,进一步验证该方法的有效性。模拟数据由如下模型产生:
yi=μi+σεi,εi~N(0,1),i=1,…,n,
(23)
其中数据长度n=500,噪声参数σ=0.2。数据中共存在6个均值变点,变点位置依次为137,224,241,298,307,331各个区段均值μ依次为-0.18,0.36,0.89,-0.4,0.29,-0.65,0.33,如图1所示。
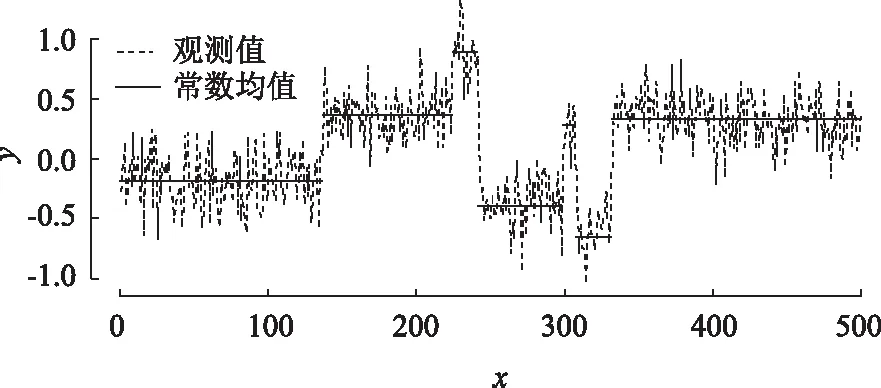
图1 模拟数据示例Fig.1 Example of simulated data
在积分均方误差准则下局部多项式回归的最优光滑参数如图2所示。从图2中可以看出,模拟数据的积分均方误差MISE在光滑度h为2.6时达到最小值;而断面流量数据的积分均方误差MISE在光滑度h为1.1时达到最小,故局部多项式的最优光滑参数分别选取为2.6和1.1。

图2 局部多项式回归光滑参数的选取Fig. 2 Selection of local polynomial regression smoothing parameters
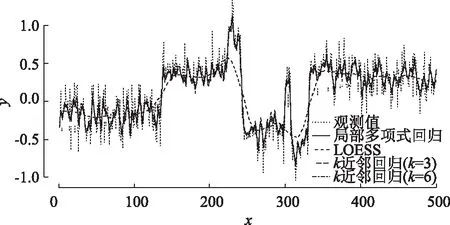
图3 局部多项式、LOESS及k近邻回归方法比较Fig.3 Comparison of local polynomial, LOESS and k-nearest neighbor regression method
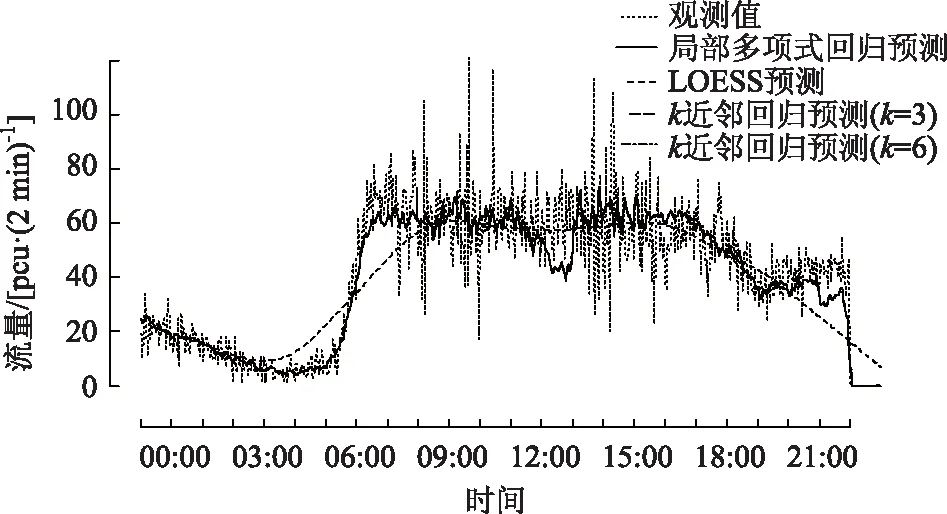
图4 局部多项式回归、LOESS及k近邻回归预测比较Fig.4 Comparison of local polynomial regression, LOESS, and k-nearest neighbor regression prediction
基于模拟数据和断面流量数据,将局部多项式回归与LOESS,k近邻等经典的非参数回归方法进行比较如图3、图4所示。从图3和图4中均可以看出LOESS方法只是大致拟合了数据的趋势,与观测时序趋势相差较大,不便于做实际分析; 而局部多项式回归与k近邻回归拟合效果相对较优,拟合时序和观测值序列趋势基本吻合。
通过比较得到各个方法的精度评价指标见表1。从表1中可以看出局部多项式回归在两个精度指标可决系数R2和均方根误差RMSE方面均表现较优。一方面基于模拟数据局部多项式、k近邻(k=3)和k近邻(k=6)的可决系数R2以及RMSE相对于LOESS较高,且局部多项式回归的R2和RMSE较优,分别为0.926 5和0.894 8,进而说明了局部多项式回归方法的有效性。另一方面基于交通流数据局部多项式回归预测值与观测值的可决系数R2为0.894 8,均方根误差RMSE为11.088 6,相对于LOESS和k近邻回归方法较优,进一步验证了该方法的有效性。
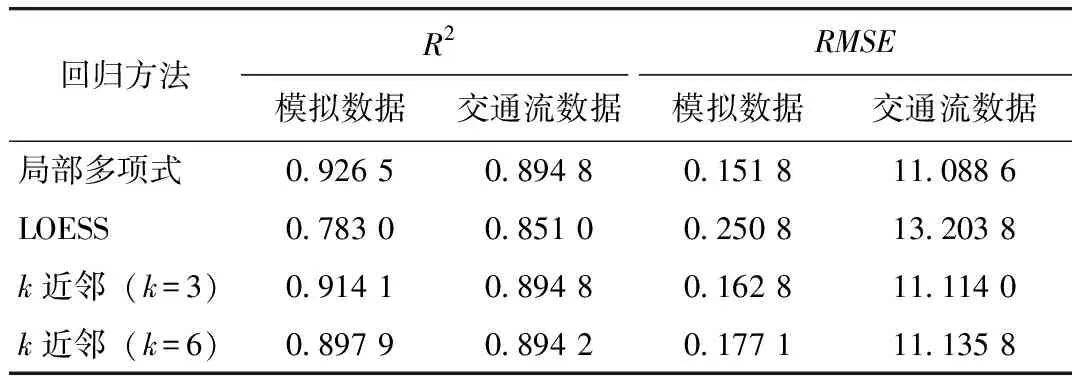
表1 精度指标比较Tab.1 Comparison of precision indicators
3 案例分析
3.1 交通流近平稳状态检测
主要选取贵阳市中山西路与瑞金中路(由南往北方向)、中华南路与都司路(由北往南方向)两个交叉口的断面交通流为研究对象,分别将其记为断面I和断面II。为检测所选断面交通流的近平稳状态以及断面交通流短期预测,特取7月1日—7月7日为期1周的2 min断面交通流数据如图5所示,从图5可以看出在07:00与23:00之间的时段内两个断面的交通流量相对较高,其余时段相对较低,特别在23:00与00:00之间的时段内数据存在不同程度的缺失或异常值,造成该时段内的近平稳状态检测结果、断面交通流量预测与实际不符,见图4、图6及图8所示。
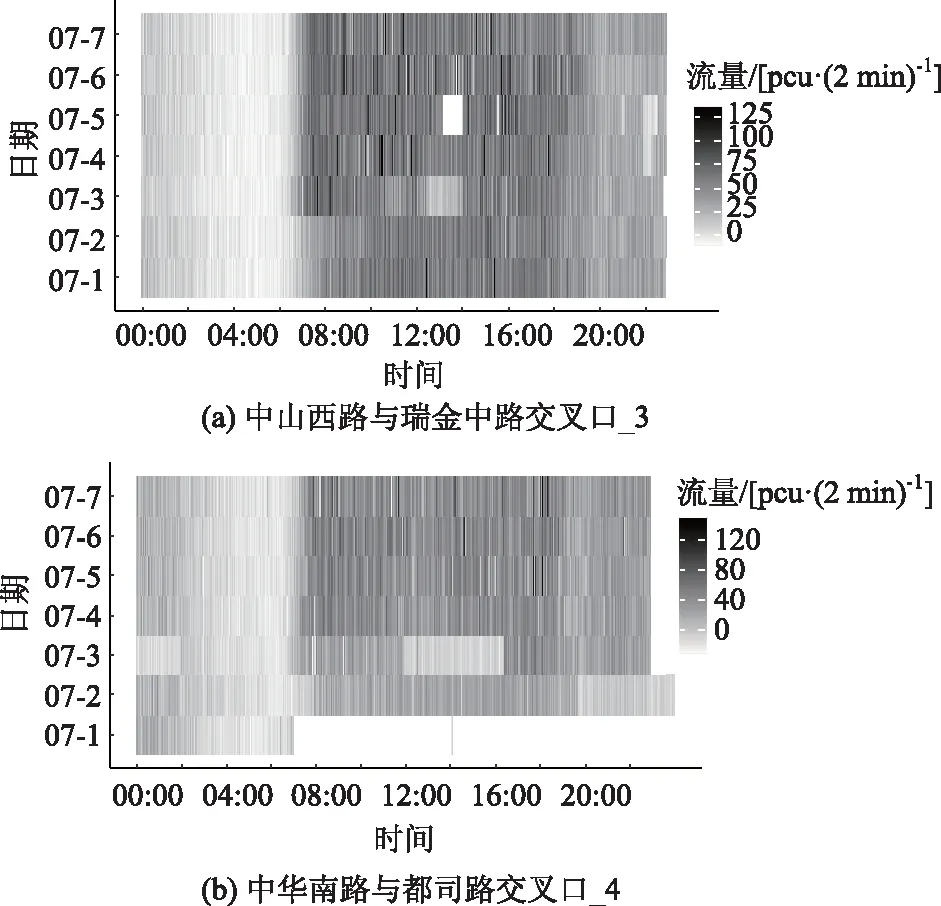
图5 断面I和断面II交通流量热力图Fig.5 Thermal diagrams of traffic volumes at section I and section II
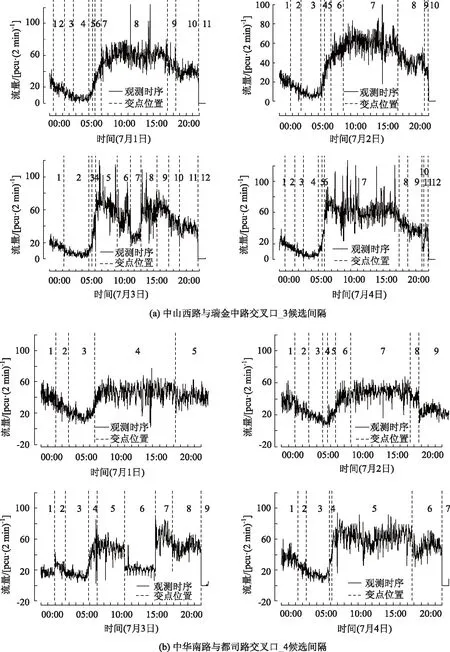
图6 断面I和断面II近平稳状态候选间隔Fig.6 Near-stationary state candidate intervals of section I and section II
为检测出所选断面处的交通流近平稳状态,采用基于动态规划和剪枝技术的PELP算法对断面交通流序列进行候选间隔的划分如图6所示,图6(a),(b)中仅显示了7月1日—7月4日的近平稳状态候选间隔,并对所划分的候选间隔进行编号。针对断面I和断面II为期1周的交通流量序列共划分出131个候选间隔,其中断面I包含56个候选间隔,断面II包含75个候选间隔。对所有候选间隔进行ADF检验,将ADF值严格小于0且p值不超过显著性水平0.01的候选间隔视为近平稳状态,共检测出55个近平稳状态,其中断面I包含28个近平稳状态,断面II包含27个近平稳状态。
例如,7月2日断面I与断面II候选间隔状态检测结果见表2。对于检测出的非平稳状态,其对应时段内的断面流量会出现较大的波动,更容易导致交通事故的发生,具体需结合多源交通流数据做进一步排查,该检测结果对道路交通管理具有一定的有效性。
3.2 近平稳状态的验证
根据Cassidy提出的目视检测方法[25]对近平稳状态有效性进行直接验证,记N(t,l)为t时刻到达位置l的累计车流量,q0t为时间的线性函数,q0是与候选间隔有关的常数,若N(t,l)-q0t关于时间t具有线性趋势且与最佳拟合线之间的偏差不超过10 辆-1,则该候选间隔可以视为近平稳状态。为说明上述所检测出的近平稳状态是有效的,以7月2日断面II时段[05:52, 09:54]为例,该时段共划分了3个候选间隔,累计车流量的原始曲线N(t,l)和转换曲线N(t,l)-q0t如图7所示。从图7中可以直观的看出:第4个候选间隔不仅具有明显的线性趋势且均在拟合线阈值边界内,所以该候选间隔视为近平稳状态是有效的; 注意到第5个和第6个候选间隔没有被选为近平稳状态,很大程度上是因为累计车流量转换曲线超出拟合线阈值边界。这与表2中断面II的近平稳状态检测结果是一致的,即上述所构建的交通流近平稳状态检测方法是有效的。

表2 7月2日断面I与断面II候选间隔状态检测结果Tab.2 Test result of candidate interval between section I and section II on July 2

图7 累计车流量原始曲线和转换曲线Fig.7 Original and transformed curves of cumulative traffic volume
3.3 交通流短期预测
除了对断面交通流进行状态检测外,为了提高道路的交通流趋势预警,在PELT变点检测算法的基础上将局部多项式回归与Sigma原则结合,得到短期断面交通流趋势预测区间。

(24)
式中,n为预测样本量;I(·)为示性函数。
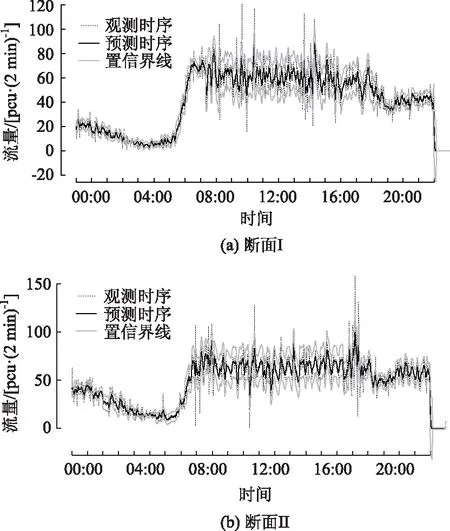
图8 7月7日短期断面交通流趋势预测Fig.8 Cross-sectional short-term traffic flow trend prediction on July 7
以7月1日—7月6日的断面交通流数据为测试集,基于测试集数据采用上述局部多项式回归,得到7月7日的短期断面交通流趋势预测如图8所示,从图8中可以看出部分时段的交通流量会出现较大的波动,整体上预测区间趋势与观测时序基本吻合。以断面I的预测趋势为例,如图8(a)在时段[06:00, 08:30)内共检测出5个变点,变点位置依次为06:24,06:42,07:00,07:18,08:18对应的断面流量预测值分别为11,27,42,61,65。相对于流量趋势较为平稳的时段[00:00, 06:00)而言,在该时段内流量呈现急剧上升趋势。一方面,若提前对出行者发布该断面处的交通流量趋势,则在某种程度上对出行者的路线选择提供便利,同时也有利于交管部门对该断面及时进行交通疏导,缓解交通拥堵,说明上述的短期断面交通流趋势预测区间具有一定的时效性;另一方面,断面I、断面II的交通流量趋势预测区间覆盖率分别为82.92%,80.28%,可见预测区间覆盖率较高,进一步说明了上述预测方法具有一定的有效性。
4 结论
针对目前的交通流基本参数,考虑时空特征,从统计角度随机化交通流基本参数,同时给出了相应的自由流、中断和拥堵等交通状态划分,通过分析表明近平稳状态存在于3种状态之中。针对卡口数据构建了交通流近平稳状态的检测方法。该方法能够快速准确地检测断面交通流候选间隔是否为交通流近平稳状态,并基于贵阳市实际交通流数据通过Cassidy目视检测方法验证了所提方法的有效性。除了对断面交通流进行状态检测外,为了提高道路的短期交通流趋势预警,引入局部多项式回归,对断面交通流趋势进行短期预测。通过模拟和预测精度指标比较分析表明,该方法相对于经典的LOESS以及k近邻等非参数回归方法在预测精度方面表现较优。除此之外,通过实证分析表明短期断面交通流趋势预测区间与观测时序的趋势基本吻合,且交通流趋势预测区间的覆盖率较高。综合考虑交通流近平稳状态检测结果和交通流趋势预测结果,对于出行者的路线选择、交通拥堵的缓解以及交管部门的决策提供了一定的参考价值。同时为道路交叉口及城市路网中交通流近平稳状态的自动检测提供了方法参考。
所提方法不足之处在于PELT变点检测方法不仅要求数据服从正态分布,而且易受异常值的影响。在分布假设不正确或异常值存在的情况下,可能会影响时序的划分,进一步影响检测的近平稳状态数量和质量。因此在后续研究中可以考虑一些稳健的时序划分方法,来增强近平稳状态检测方法对异常值的稳健性。另外,在接下来的工作中将通过基本图对多时段、多断面交通流数据进行精细划分交通状态以及多断面交通流短期预测方法的研究。
