电比例斜轴式柱塞泵特性仿真分析及试验

文晨阳， 李毅波，， 潘 晴，3， 王照卓

(1.中南大学 机电工程学院， 湖南 长沙 410083； 2.中南大学 轻合金研究院， 湖南 长沙 410083；3.浙江大学 流体动力与机电系统国家重点实验室， 浙江 杭州 310027)

引言

工程机械智能化、节能化以及操作简便化的发展趋势，对柱塞泵的动态响应速度与控制精度提出了越来越高的要求，精确建立柱塞泵的数学模型，系统研究柱塞泵在不同工况下的响应特性，并以此为基础，通过高精度电液比例控制技术提高柱塞泵及液压驱动系统的稳定性、控制精度与能效[1]，是目前工程机械领域研究的热点问题。

JANNE K等[2]针对变排量柱塞泵的控制系统，以控制压力为被控对象，控制阀电压为控制变量，提出了一种基于模型自适应的非线性控制方法，建立了自适应控制器并与所建立的柱塞泵运动模型结合，实现了对柱塞泵电控系统中高度非线性行为的精确控制。QING L等[3]建立了活塞环-缸内孔界面(PRCB)最小油膜厚度模型，将最小油膜厚度模型与流动方程相结合，建立了PRCB的数学模型，得到了油膜对PRCB泄漏量的影响，从而得到了柱塞泵泄漏量与转速间精确的关系。ZHANG Peng等[4]建立了电比例轴向柱塞泵的数学模型，提出将PID控制方法、基于反馈线性化方法的线性二次调节器(LQR)和反推滑模控制方法引入其控制系统，实现了在外部干扰下对柱塞泵压力的精确控制。高有山等[5]通过将配流盘流量方程和斜盘动力学方程引入变排量非对称轴向柱塞泵的AMESim模型中，通过对柱塞泵关键结构参数进行测量，得到了更精确的柱塞泵斜盘受力特性仿真分析模型。李会妨[6]针对不同软件间联合仿真数据交换带来的仿真速度降低的问题，基于多学科联合仿真软件SimulationX搭建了电控恒压柱塞泵的机液联合仿真模型对柱塞泵的动静态特性进行研究，降低了传统多软件联合仿真带来的建模难度。

目前对于电比例泵的研究主要针对的是斜盘式结构的柱塞泵[7]，对于斜轴式结构电比例泵的研究相对较少，目前已有的关于斜轴式结构柱塞泵的研究多集中于内部结构分析以及驱动方式[8-10]，涉及电比例斜轴式柱塞泵变量原理的研究较少。电比例斜轴式柱塞泵作为目前广泛应用于工程机械液压系统的核心部件之一[11-12]，对其结构与变量原理进行分析，建立其元件的数字化仿真和测试模型，对于优化工程机械工作性能，实现产品性能提升具有重要意义。

本研究以某型工程机械的电比例斜轴式柱塞泵为研究对象，在分析该型柱塞泵的泵体结构与变量机构的变量原理与工作特性的基础上，应用液压仿真软件AMESim建立了电比例斜轴式柱塞泵的数字仿真模型，实地测绘了泵体关键结构的结合尺寸与力学特性，实现了元件级高精度模型的建立；搭建了用于验证柱塞泵仿真模型效果的油泵性能测试平台，对该型柱塞泵进行了相关稳态与瞬态性能的测试。对比了仿真模型结果与试验结果的静动态误差，验证了模型的正确性与仿真结果的准确性。

1 电比例斜轴式柱塞泵工作原理

本研究中斜轴式柱塞泵的内部结构如图1所示，柱塞泵由基泵与变量机构两部分组合而成。基泵结构主要包含驱动轴、中心杆、柱塞、缸体和配流盘等组件；变量机构部分由变量活塞、连杆、反馈弹簧以及电比例控制阀等组件构成。当泵工作时，驱动轴进行旋转运动，带动缸体与柱塞旋转，驱动轴和缸体之间存在着一个倾角，使得柱塞在进行旋转运动的同时也会沿着缸体进行直线往复运动，从而实现吸油与压油的功能。

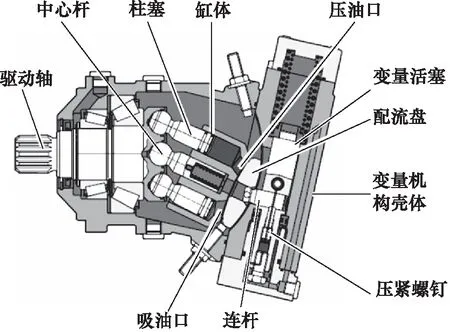
图1 斜轴式轴向柱塞泵内部结构图Fig.1 Internal structure diagram of inclined axis axial piston pump

电比例斜轴式柱塞泵的液压原理图如图2所示，柱塞泵变量机构中的变量活塞通过反馈弹簧与电比例控制阀相连，通过控制电比例控制阀的输入电流来改变比例电磁铁产生的电磁力，从而推动控制阀阀芯移动来改变变量活塞缸的油路流通状况，使得变量活塞发生运动从而带动缸体转动，柱塞泵缸体与传动轴的角度发生变化使得柱塞泵输出排量发生改变。与此同时变量活塞的移动也会压缩反馈弹簧将力传递给电比例控制阀的阀芯，使得变量机构处于一个新的平衡状态。

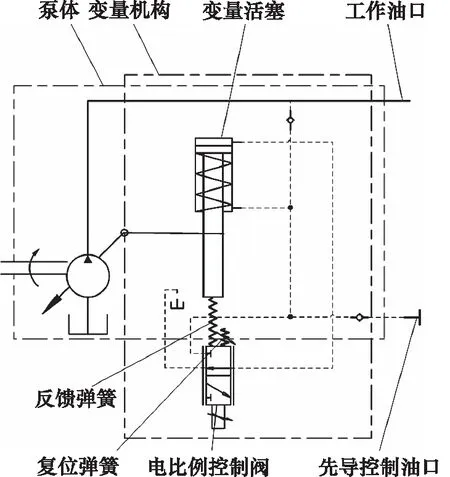
图2 电比例斜轴式柱塞泵液压原理图Fig.2 Hydraulic schematic diagram of electric proportional inclined axis plunger pump

由图3电比例斜轴式柱塞泵的变量特性曲线可以看出，该柱塞泵的排量与电比例控制阀输入的控制电流呈线性比例关系，排量大小随着电流大小的增长而增长，但在变排量过程中存在一个死区电流值与饱和电流值，当控制电流为死区电流值时，泵排量始终为0，不发生改变，当控制电流达到饱和电流值时，柱塞泵输出最大排量，排量不再随着电流的增大而增大。

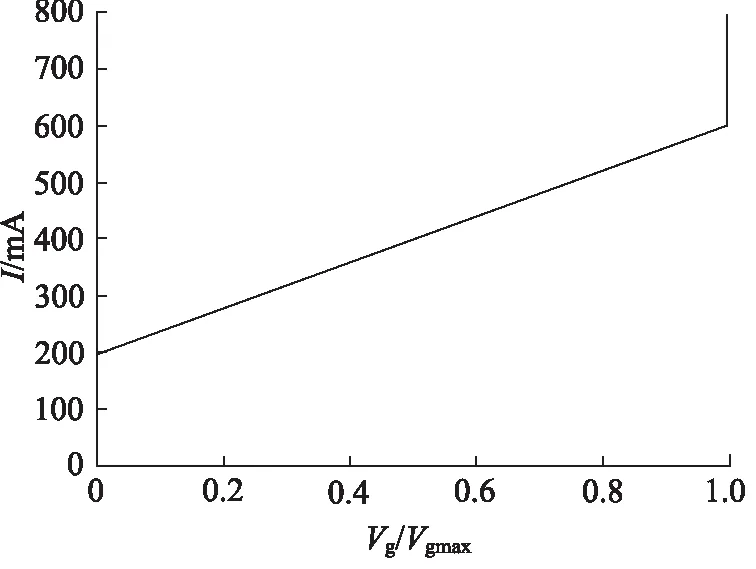
图3 电比例斜轴式柱塞泵变量特性曲线Fig.3 Variable characteristic curve of electric proportional inclined axis plunger pump

2 电比例斜轴式柱塞泵数学模型

2.1 变量机构数学模型

该柱塞泵变量机构的控制系统属于阀控缸系统，通过二位三通的比例电磁阀来控制变量柱塞缸移动实现排量的改变，其工作原理图如图4a所示，其中电比例控制阀的内部结构图如图4b所示[13]，由图4b可知，该控制阀阀口由4个圆形阀口组成。

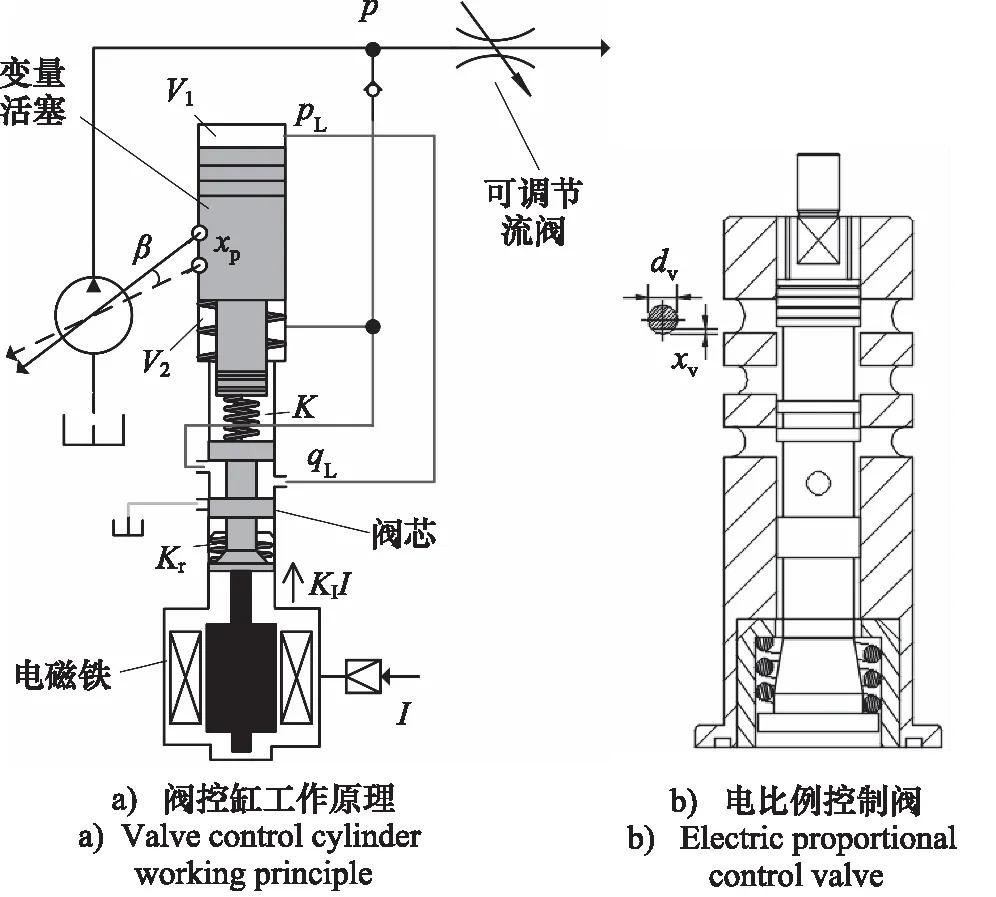
图4 电比例斜轴式柱塞泵变量机构结构图Fig.4 Structure diagram of variable mechanism of electric proportional inclined axis plunger pump

圆形阀口的通流面积为弓形，单个阀口通流面积为：

(1)

式中,dv—— 控制阀阀口直径

xv—— 阀芯位移

圆孔阀口通流面积的面积梯度为：

(2)

由图4b可知，该电比例控制阀为双边滑阀，阀芯向下移动，xv<0时，阀口压差为：

(3)

式中，p—— 油源油压

pL—— 变量活塞腔的压力

流出液压缸压力流量方程[14]为：

(4)

式中，qL—— 阀口通过的流量

Cd—— 阀口的流量系数

ρ—— 液压油密度

阀芯向上移动，xv>0时控制阀阀口压差为：

(5)

流入液压缸压力流量方程为：

(6)

电比例控制阀的流量增益为：

(7)

电比例控制阀的流量-压力系数为：

(8)

电比例控制阀的压力增益为：

(9)

电比例控制阀阀芯在电磁铁、复位弹簧以及反馈弹簧作用下的力平衡方程[15]为：

(10)

式中,KI—— 电磁铁的电磁力比例系数

I—— 电比例控制阀的输入电流

mv—— 控制阀阀芯质量

Bv—— 阀芯阻尼系数

xp—— 变量活塞位移

K—— 反馈弹簧刚度

Kr—— 复位弹簧刚度

Fr—— 复位弹簧预紧力

流入电比例控制阀的流量方程经过线性化后可得：

qL=Kqxv-KcpL

(11)

对式(11)进行拉氏变换可得：

QL(s)=KqXv(s)-KcpL(s)

(12)

流入液压缸控制腔V1的流量连续性方程为：

(13)

式中，A1—— 变量活塞缸大腔的面积

C1p—— 液压缸的泄漏系数

V1—— 变量活塞缸大腔的体积

β1—— 油液的有效弹性模量

对式(13)进行拉氏变换可得：

(14)

变量活塞缸工作腔的容腔体积为：

V1=V0+A1xp

(15)

式中，V0为变量活塞大腔初始容腔体积。

变量活塞的力平衡方程[15]为:

(16)

式中，A2—— 变量活塞缸小腔面积

mp—— 变量活塞质量

Bp—— 变量活塞阻尼系数

将式(16)经拉氏变换可得：

PL(s)A1=(mps2+Bps+K)Xp(s)+Ps(s)A2

(17)

为了使公式简化，令Kc1p=Kc+C1p，则由式(13)、式(15)、式(18)可得变量活塞位移为：

(18)

2.2 泵体数学模型

对图1中斜轴式柱塞泵的结构进行分析可知，其排量的改变主要是靠变量控制阀控制变量活塞运动，通过固定在变量活塞上的连杆来带动缸体转动从而使得柱塞泵工作角度改变来改变排量。现对其变量过程中的数学关系进行分析，绘制斜轴式柱塞泵的泵体结构简图及几何简图，如图5所示[16]。

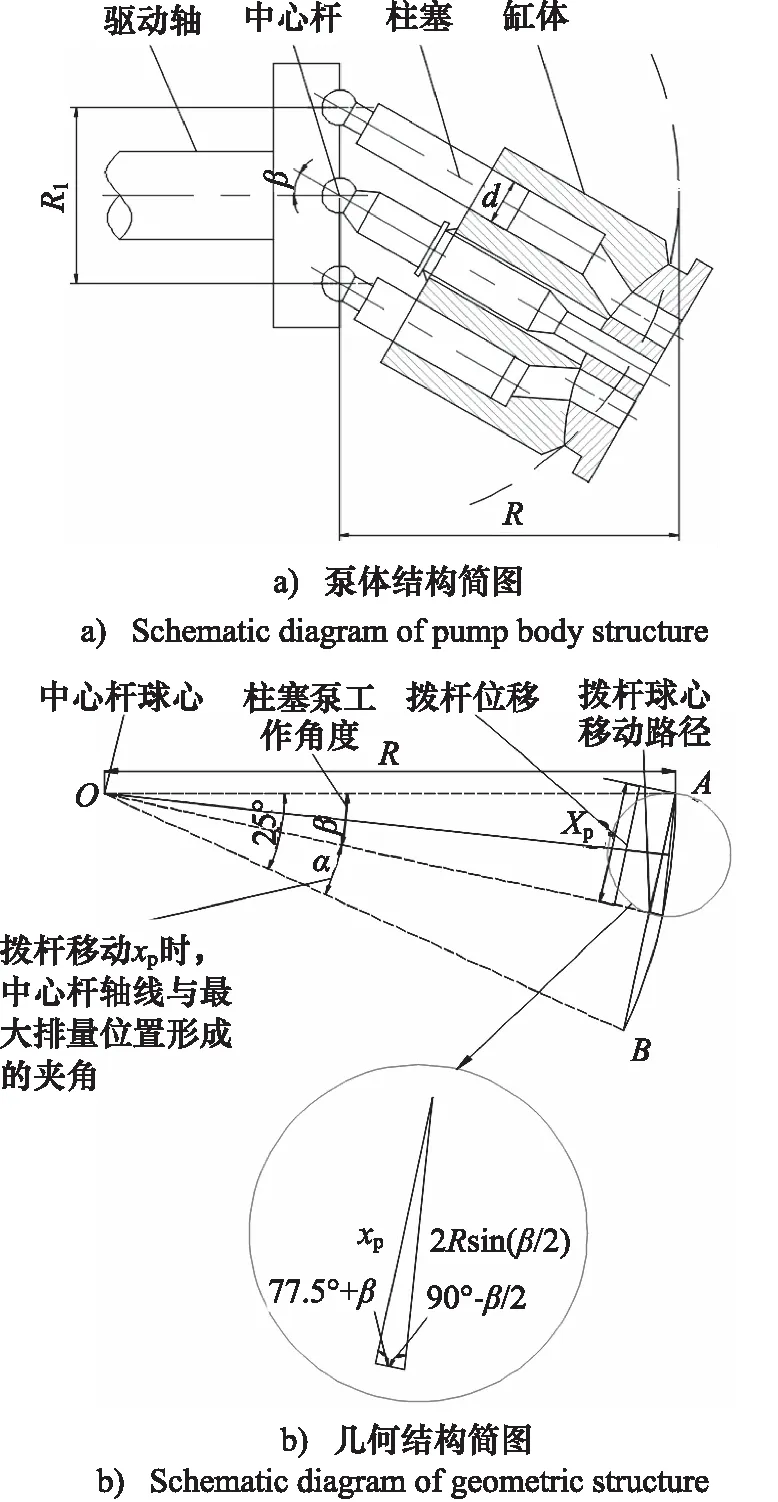
图5 斜轴式柱塞泵结构简图Fig.5 Structure diagram of inclined axis plunger pump

柱塞泵的工作角度与拨杆的位移有关，如图5b所示，以中心杆的球心为圆心，零排量与最大排量时连杆与配流盘的接触中心为端点， 构成了圆弧AB， 半径为R。在图中所示三角形中根据正弦定理可得：

(19)

式中,β—— 柱塞泵的工作角度

可以求出当连杆位移为xp时缸体转动的角度为：

(20)

缸体初始角度为0°，则缸体转过的角度即为柱塞泵的工作夹角，因此可以计算出柱塞泵的理论排量为：

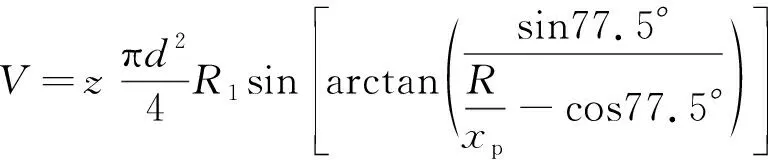
(21)

式中，z—— 柱塞个数

d—— 柱塞直径

R1—— 柱塞在卡盘上的分布圆半径

柱塞泵在实际工作时泵体存在着流量的泄漏，主要来源于柱塞在运动过程中与柱塞腔之间的泄漏[17-18]，柱塞在柱塞腔中运动简图如图6所示，可得柱塞泵的泄漏量为：

(22)

式中, Δpl—— 柱塞腔与油口压差

μ—— 油液动力黏度

lc—— 接触长度

rc—— 径向间隙，rc=dc/2

e—— 偏心量

vp—— 柱塞与缸体相对运动速度

所以柱塞泵实际输出流量为：

(23)

式中，Q—— 柱塞泵实际输出流量

V—— 柱塞泵的理论排量

n—— 电机转速

i—— 柱塞代号

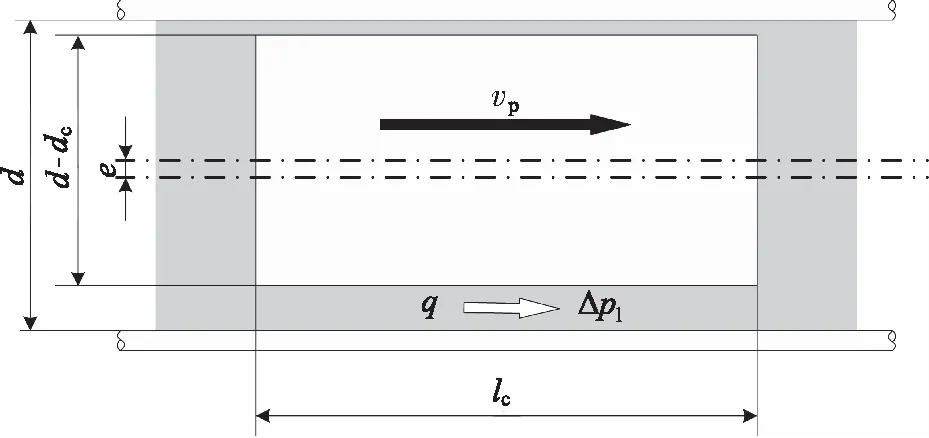
图6 柱塞腔流量泄漏结构简图Fig.6 Schematic diagram of flow leakage structure of plunger cavity

3 柱塞泵特性仿真分析

根据已建立的相关数学模型，通过AMESim软件平台，搭建了电比例斜轴式柱塞泵数字化仿真模型如图7所示，并对相关结构参数对于柱塞泵性能的影响进行了仿真分析[19]。该柱塞泵模型主要由变量机构、泵体结构、加载模块以及电控信号模块组成。模型中各关键结构参数由机械结构测绘获得，如表1所示。

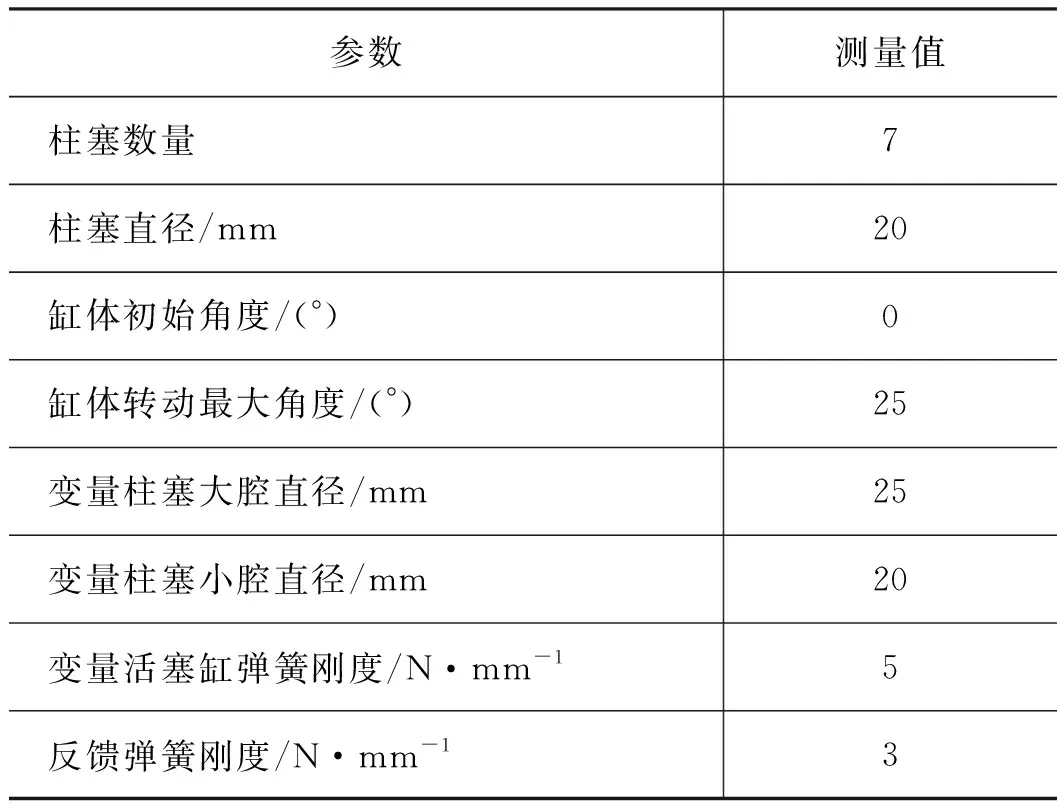
表1 电比例斜轴式柱塞泵结构参数Tab.1 Structural parameters of electric proportional inclined axis plunger pump

图7中根据式(1)～式(9)选用AMESim相应的阀口模块完成对电比例控制阀阀芯模型的建立，设置反馈弹簧、复位弹簧和比例电磁铁建立起式(10)中阀芯的受力关系。由式(11)～式(16)完成变量活塞缸模型油路的连接以及与反馈弹簧的结构连接，实现阀控缸部分位移与力的传递关系，通过位移传感器将变量活塞位移输入给柱塞位移-缸体角度转换模块，通过转换方程式(20)驱动缸体转动。泵体结构部分由柱塞模型和配流盘结构模型构成，柱塞模型根据式(22)设置了相应的泄漏。加载模块通过一个电比例溢流阀来实现。电控信号模块由控制电流输入信号、电流-电磁力转换模型以及滞环系数模型组成，控制电流信号值即为电比例斜轴式柱塞泵的输入电流值，控制电流通过电流-电磁力转换模型输出电磁力给电比例控制阀阀芯从而驱动变量机构工作，滞环系数模型用来模拟电比例泵的电磁元件在工作过程中出现的滞环现象。加载模块后的流量传感器可以读出柱塞泵的输出流量，其流量值满足式(23)。

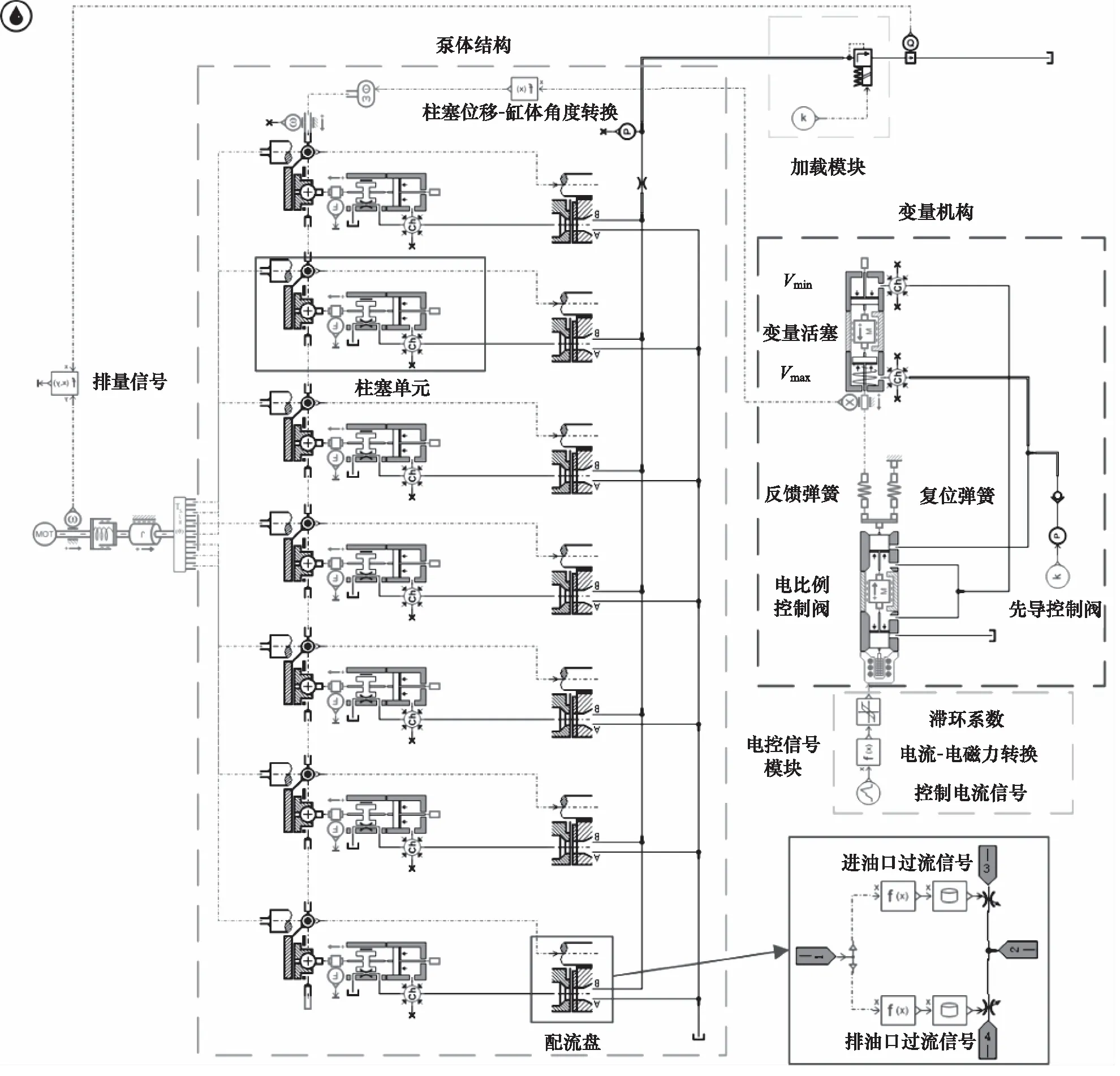
图7 电比例斜轴式柱塞泵AMESim仿真模型Fig.7 Simulation model of electric proportional inclined axis plunger pump based on AMESim

泵体结构部分的建模精度与配流盘的结构关系密切[20]，此次配流盘的模型通过对图8a中配流盘的实际结构进行参数测量，在AMESim中搭建了柱塞泵配流盘的仿真模型，如图8b所示。

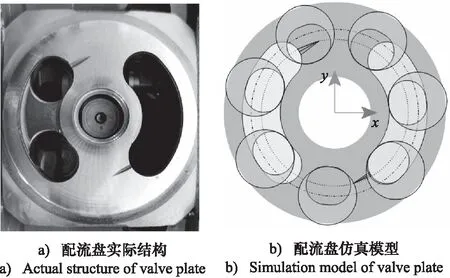
图8 配流盘结构图Fig.8 Valve plate structure diagram

根据配流盘AMESim计算机仿真模型可以计算出配流盘进出油口配流面积S随缸体回转角度θ的变化关系，如图9所示。将所得的配流盘过流面积作为配流信号输入图7中的配流盘进油口过流信号与排油口过流信号当中[21]。

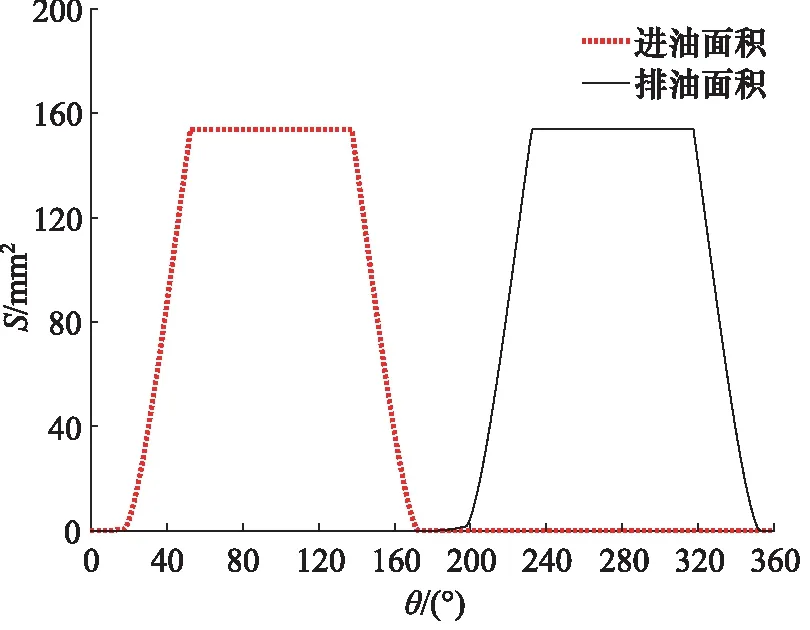
图9 配流盘配流面积Fig.9 Distribution area of distribution plate

电比例斜轴式柱塞泵的初始工作角度为0°。泵转速为1000 r/min，负载压力为16 MPa时，输入控制电流信号从0 mA增加至650 mA，之后从650 mA下降至0 mA时的电流-流量曲线，如图10所示。可以看出，电比例斜轴式柱塞泵在工作过程中存在死区电流与饱和电流，同时电流信号下降时的流量变化滞后于电流信号上升时的流量，电比例柱塞泵存在一定的滞环效应。

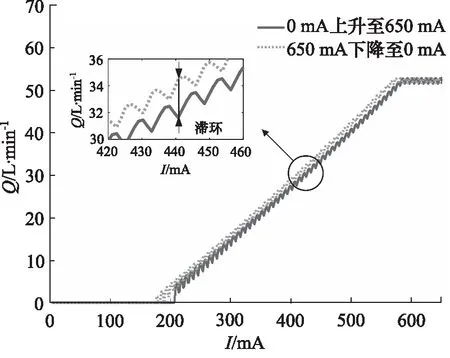
图10 电比例斜轴式柱塞泵电流-流量仿真曲线Fig.10 Electric proportional inclined axis plunger pump current-flow simulation curve

对变量机构中反馈弹簧的刚度特性进行分析，设置泵转速为1000 r/min，负载压力为16 MPa，电流信号从0 mA上升至800 mA，反馈弹簧的刚度分别设置为3.0， 3.5， 4.0 N/mm，仿真结果如图11所示。可以看出，随着反馈弹簧刚度的增大，柱塞泵流量上升的速率下降，死区电流未发生改变，但饱和电流随着反馈弹簧刚度增大而增大，饱和流量值相同。

图11 不同反馈弹簧刚度下的电流-流量曲线Fig.11 Current-flow curve under different feedback spring stiffness

保持转速和压力条件恒定不变，电流信号从0 mA上升至650 mA，分别设置电比例控制阀阀芯复位弹簧刚度为15， 25， 35 N/mm，对阀芯复位弹簧刚度的特性进行分析，仿真结果如图12所示。

由图12可以看出，不同复位弹簧刚度下柱塞泵的流量上升速率均相同，未发生变化，但柱塞泵的死区电流值和饱和电流值均不同，随着复位弹簧刚度增大而增大。

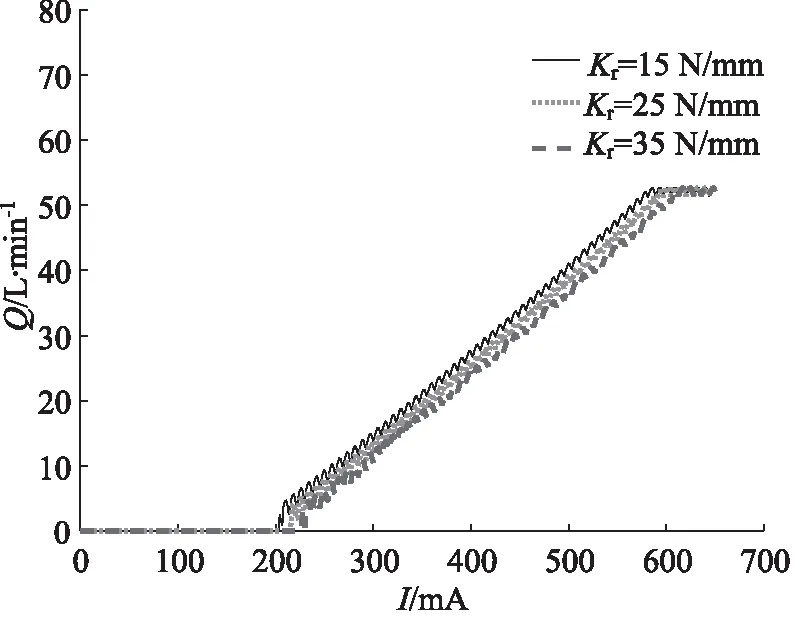
图12 不同复位弹簧刚度下的电流-流量曲线Fig.12 Current-flow curve under different return spring stiffness

4 试验验证

4.1 试验装置与方法

在国内某工程机械龙头企业柱塞泵性能测试系统中开展该型液压泵的静动态性能测试。测试试验台如图13所示，待测柱塞泵安装于试验台上，通过该试验台可以完成对液压回路中负载压力、转速、控制电流等参数的调节，通过操作面板上方的LED显示屏可以读取待测参数值的大小[22]。为了保证测试结果具有更高的精度，外接了图14所示的数据采集仪来采集油泵工作过程中的流量和压力等参数。该油泵性能测试试验台可以完成油泵各项稳态与瞬态性能的相关测试，具体测试工况如表2所示。

图13 油泵性能测试试验台Fig.13 Oil pump performance test bench

图14 测试数据采集仪器Fig.14 Test data acquisition instrument

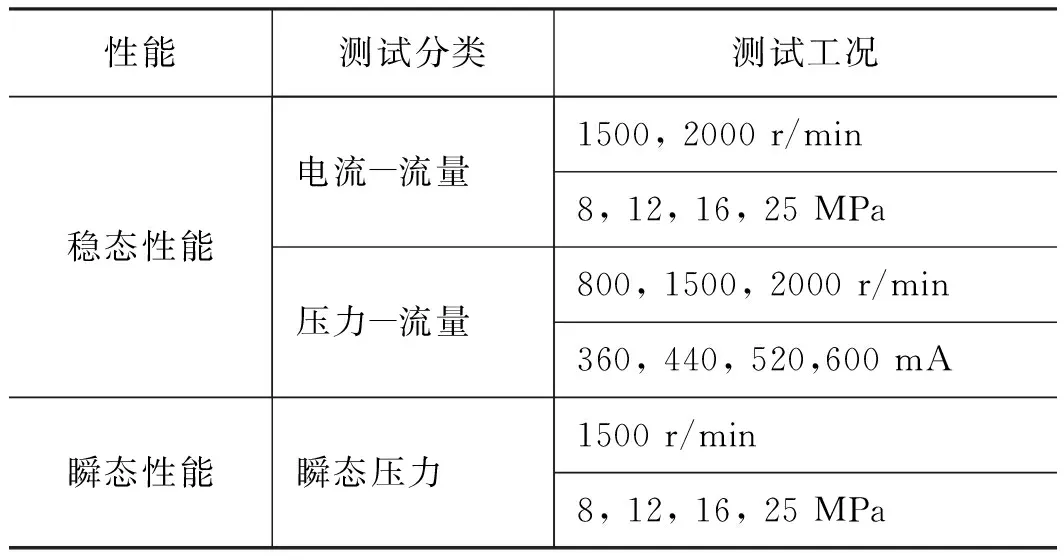
表2 电比例斜轴式柱塞泵性能测试工况Tab.2 Performance test conditions of electric proportional bent-axis piston pump

4.2 试验结果分析与讨论

转速为1500， 2000 r/min， 负载压力分别设置为8， 12， 16， 25 MPa，控制电流以30 mA为间隔从200 mA 上升至600 mA，再从600 mA下降至200 mA时，电流-流量实验测试结果与仿真分析结果对比，如图15所示,可以看出，不同转速与负载条件下的电流-流量仿真曲线与试验曲线基本吻合。

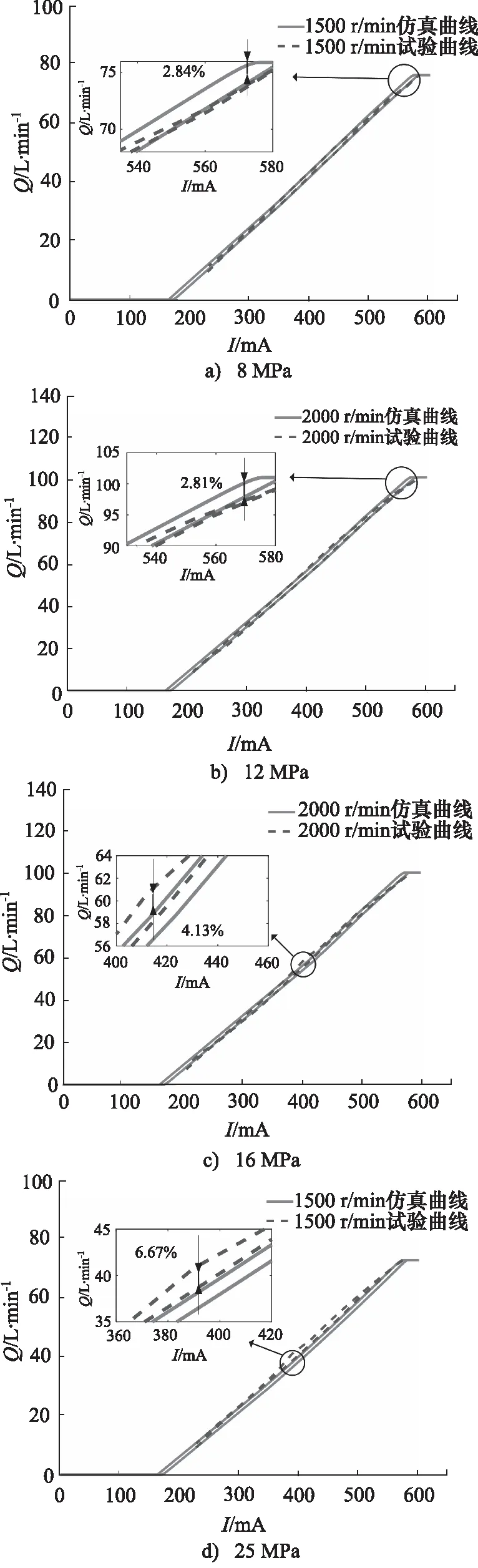
图15 柱塞泵电流-流量曲线对比Fig.15 Comparison of plunger pump current-flow curve

对每种负载下的最大误差值进行统计，如表3所示，最大误差出现在转速为2000 r/min、负载压力为25 MPa 时，仅为6.86%， 可以验证该仿真模型的电比例功能具有较高的准确度，符合实际柱塞泵元件的工作特性。

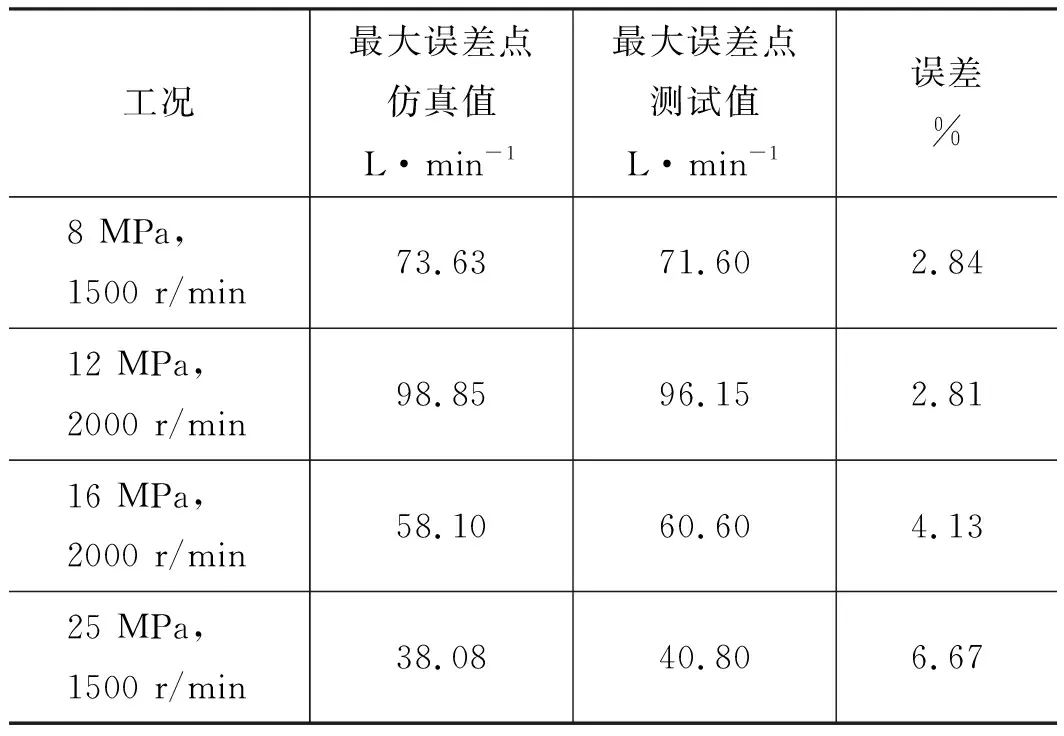
表3 电流-流量曲线最大误差值统计表Tab.3 Statistical table of maximum error value of current-flow curve

当转速分别为800， 1500， 2000 r/min，控制电流分别设置为360， 440， 520， 600 mA，负载压力以3 MPa 为间隔，从3 MPa上升至30 MPa时，得到的柱塞泵压力-流量特性曲线的试验测试与仿真分析对比情况，如图16所示，可以看出，不同转速与控制电流条件下的压力-流量仿真曲线与试验曲线基本吻合。对每种转速下的最大误差值进行统计，如表4所示， 可以看出，每种工况下的误差都较小，最大误差出现在转速为1500 r/min,控制电流为440 mA时，仅为5.77%，可以验证该柱塞泵仿真模型的压力-流量特性符合实际柱塞泵元件的工作特性。

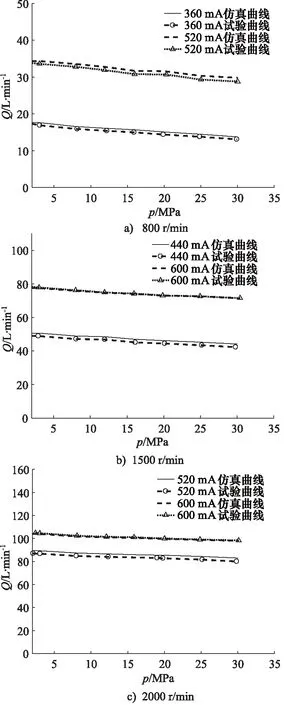
图16 柱塞泵压力-流量曲线对比Fig.16 Comparison of plunger pump pressure-flow curve

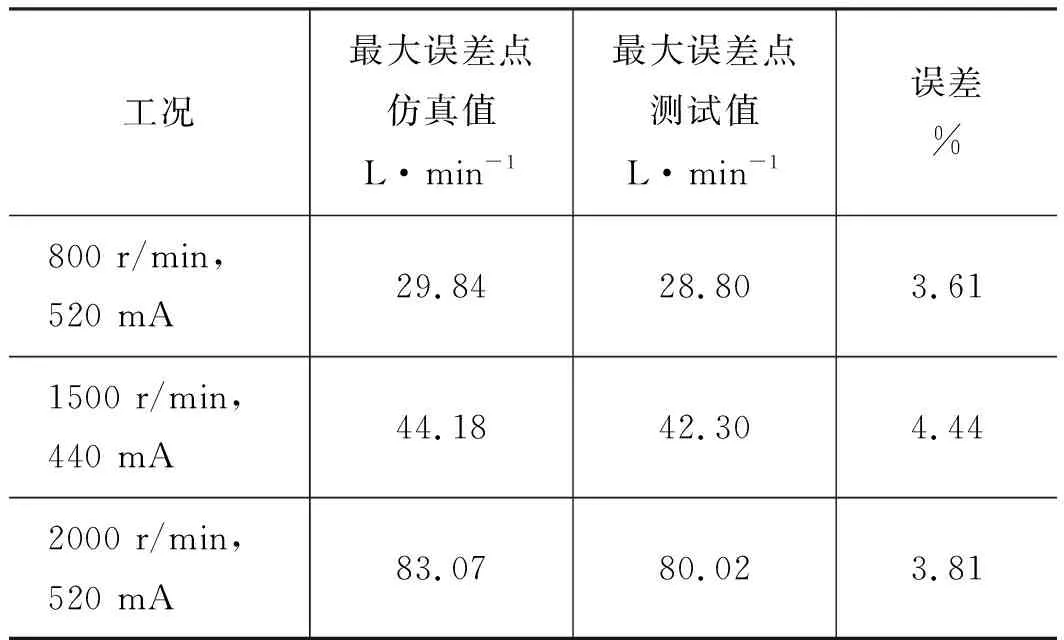
表4 压力-流量曲线最大误差值统计表Tab.4 Statistical table of maximum error value of pressure-flow curve

当柱塞泵瞬态压力响应测试分别设置转速为1500 r/min，输入600 mA控制电流使柱塞泵满排量工作,负载压力分别为8， 12， 16， 25 MPa 时，柱塞泵瞬态压力响应的实验测试与数值仿真结果的对比，如图17所示，可以看出，不同工况下仿真模型的压力响应曲线与试验曲线基本吻合。不同负载压力下仿真模型和试验结果的压力响应上升时间与下降时间统计如表5所示，可以看出，不同负载压力下柱塞泵响应时间仿真值与实测值基本一致，响应时间最大误差仅为0.02 s，可以验证该柱塞泵仿真模型的压力响应特性符合实际柱塞泵元件的工作特性。

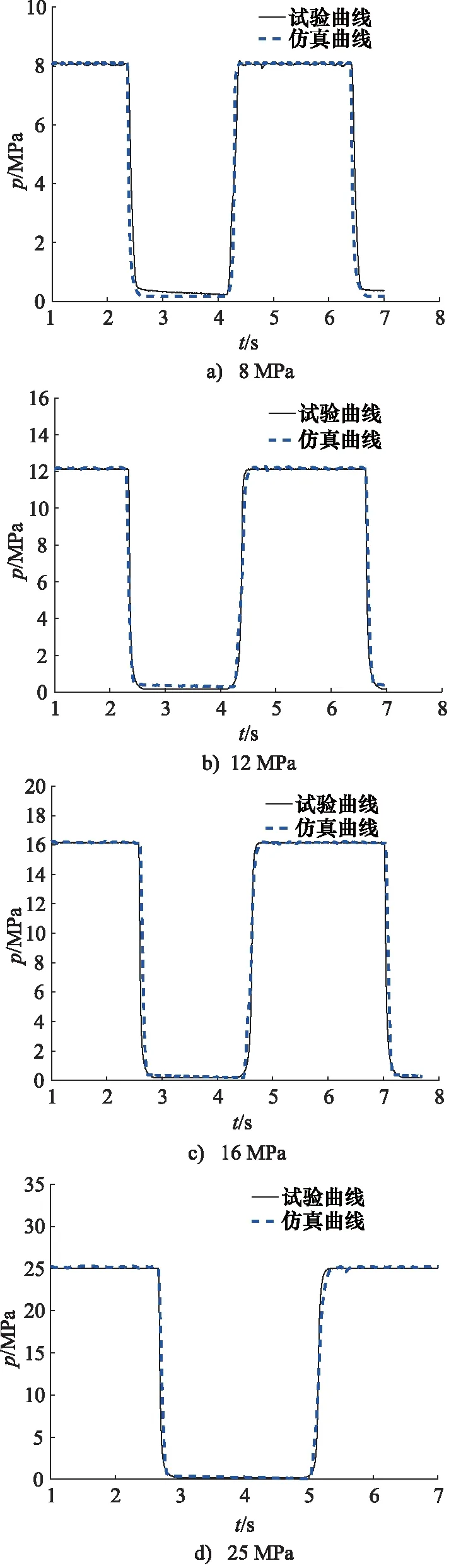
图17 柱塞泵瞬态压力响应曲线对比Fig.17 Comparison of transient pressure response curve of plunger pump

表5 柱塞泵响应时间对比Tab.5 Comparison of plunger pump response time

5 结论

(1) 推导了电比例斜轴式柱塞泵的阀控缸变量机构数学模型和包含泄漏的泵体流量计算数学模型，可以为该类型柱塞泵变量机构的结构优化与设计提供指导，搭建了配流盘的数值仿真模型，得到了该柱塞泵进油与回油过程中通流面积随缸体角度的变化关系，有利于进一步展开配流盘结构对泵体脉动特性或压力流量特性的研究；

(2) 拟定了柱塞泵关键性能的测试方案，涵盖柱塞泵的稳态性能与瞬态性能的各项测试，分析了不同性能的测试原理并制定了相关测试步骤，为相关泵类液压元件的性能测试提供了理论指导；

(3) 搭建了电比例斜轴式柱塞泵数字化模型，并通过试验验证了模型的有效性与准确性，该模型可以通过分析不同结构参数对柱塞泵性能的影响，对柱塞泵进行性能的评估与优化，有利于为机械产品数字化和智能化升级提供理论与技术支撑，降低了研发的周期与成本，与此同时，所提出的液压元件数字化建模方法可以推广应用至其他液压系统,促进工程机械领域数字孪生的发展。