多级降压调节阀流激振动特性分析

葛长榕， 徐东涛， 李 颖， 安 龙， 刘月娟

(1.辽宁科技大学 机械工程与自动化学院， 辽宁 鞍山 114051； 2.鞍山拜耳自动化有限公司， 辽宁 鞍山 114300)

引言

在现代管路系统中，调节阀是不可缺少的元件之一，能起到调节和稳定流量与降压的作用[1-3]。随着科技发展，生产一线对管路系统可靠性、声污染等方面的要求越来越高，这就对调节阀内部节流元件的设计合理性提出更高要求[4]。为起到节流、降压等作用，调节阀的节流结构有迷宫盘片式、窗口式和多孔型套筒式等[5-6]。高性能调节阀的关键技术尚未完全攻破，其在使用中可能存在振动等诸多问题[7]。调节阀内流道为小孔联通的多腔结构，阀内介质流动状态为极其复杂的湍流流动，在节流元件尾端可能会存在涡的形成、发展、消退过程，极易引起流量失稳、压力失衡，形成脉动冲击。这种脉动冲击存在主频率，当其主频率与调节阀的固有频率相等或相近时，将会引发流激共振[8]。这种共振会引起阀内件巨大的变形，产生强噪声，严重时还会影响生产线人员的安全。

为解决实际工况下调节阀的流激共振问题，SALIM E B等[9]基于声流固多场耦合提出阀门流激振动的单自由度模型，验证了流体激振是弹簧式阀芯阀门振动的主要原因；YOUN C等[10]基于CFD对压缩空气通过节流孔与径向狭缝结构流动进行了分析，得到了不同流动状态下压力脉动曲线。陈佳等[11]基于Fluent对射流管伺服阀的前置级瞬态流场进行分析。郭涛等[12]基于LES与流固耦合插值算法，得到光滑直管中流激振动的振源主要来自流体的脉动压力。

本研究利用ANSYS Workbench平台下Fluent模块，对多级降压调节阀进行先稳态后瞬态的内流场数值仿真模拟，得出监测点和流固耦合面压力脉动的频率范围，确认流激振动主频率；采用热流固耦合模态分析代替传统静力学模态分析，得出标准工况下调节阀固有频率，并与前者对比，验证调节阀是否会发生流激共振现象。

1 多级调节阀结构与标准工况

多级降压调节阀结构如图1所示，调节阀主要由阀体、阀座、多孔套筒、阀塞、压笼、阀盖和阀杆零件组成。调节阀的阀杆在外部执行器的作用下，带动阀塞上下移动改变内层套筒上节流孔的有效节流面积，从而实现流量调节，同时也有较好的降压功能。外两层多孔套筒可以降低阀内介质流动的流速，将阀两端的高压差逐级降压，有效防止闪蒸、空化现象产生。

图1 多级降压调节阀结构Fig.1 Structure of multi-stage pressure reducing valve

2 调节阀瞬态模拟前处理

2.1 瞬态流场湍流模型选择

本研究采用RNGk-ε湍流模型进行多级降压调节阀瞬态流场模拟。RNGk-ε模型是在Standardk-ε模型基础之上发展而来，在复杂流场流动问题中，RNGk-ε模型已经被证明比Standardk-ε更准确，但收敛性更难[13-14]，其控制方程如下：

湍动能k方程：

(1)

湍流耗散率ε方程：

(2)

式中，Gk—— 平均速度梯度引起的湍动能生成项

ρ—— 介质密度

μ—— 介质黏度

2.2 监测点与耦合面

为了得到流体作用于多级降压调节阀的压力脉动信息，对流固耦合面的压力脉动时域信息进行监测，流固耦合面如图2a所示。同时为提取调节阀内流体的压力脉动，需设置相应的压力脉动的监测点，从而导出各监测点的压力脉动时域信息。共设置13个监测点，监测点P1～P9均分布于流体流道对称面的中心线处，监测点S1，S2对应P1径向近壁面，监测点S3，S4对应P9径向近壁面，如图2b所示。

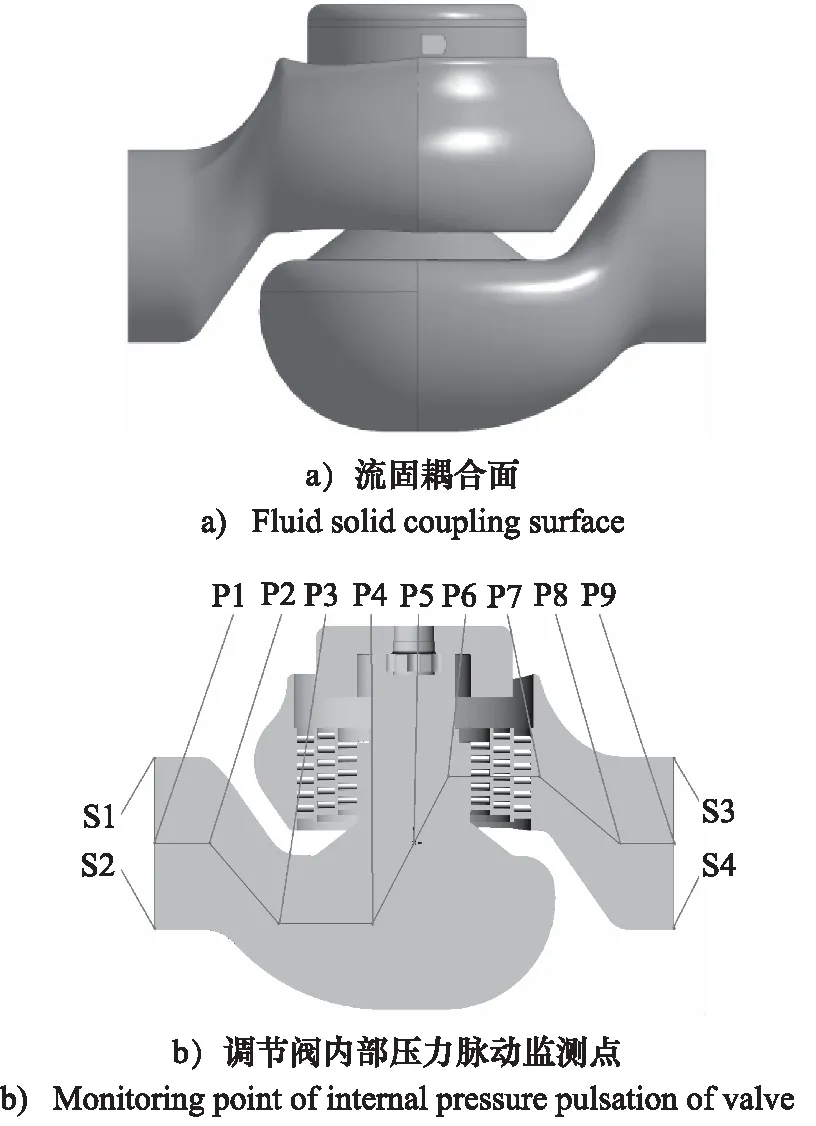
图2 监测点与监测面说明Fig.2 Description of monitoring points and monitoring surfaces

2.3 模型建立与网格划分

利用Solidworks三维软件建立DN250多级降压调节阀。通过反向建模生成对应的流体模型，将流体模型划分进口流道、阀体、出口流道三大部分，不同部分采用不同有限元网格形式，以提高仿真效率，如图3所示。调节阀内流场介质为液态水，流量为直线型流量特性，调节阀实际工况如表1所示。由于调节阀具有平面对称性，为减少计算量，提高仿真计算效率，在全模型的中截面处设置对称边界条件，仿真时采用一半模型。

图3 调节阀流体模型Fig.3 Fluid model of valve

表1 调节阀标准工况参数Tab.1 Standard operating parameters of valve

使用ANSYS Meshing软件进行网格划分，采用四面体/六面体混合网格，对多孔套筒的节流孔处进行局部加密处理，同时对划分后网格进行网格无关性验证。网格无关性参考值以最大开度稳态条件下得到的调节阀出口流量以及出口流体平均流速大小作为判断依据，具体数据如表2所示。

表2 流体网格无关性检验数据Tab.2 Fluid grid independence test data

由表2可知，网格数量从5177818进一步细化到6361212时，出口流速与出口流量值均没有明显变化，均在0.5%以内，可以忽略不计，此时满足网格无关性要求，网格模型如图4所示。

图4 调节阀流体网格模型Fig.4 Fluid mesh model of valve

2.4 瞬态模拟参数设置

边界条件：入口、出口压力、温度均按表1设置；采用标准、无滑移壁面函数；初始条件：以同工况稳态场作为瞬态场的初始值，以达到加速收敛的目的；稳态与瞬态求解采用压力基求解器、Couple算法，其余采用二阶迎风格式保证计算精度。考虑重力加速度对流体流动的影响，时间步长设置0.00025 s，时间步数设置8000，计算2 s内调节阀内部的流体流动情况。对小开度(10%)、中等开度(50%)、全开(100%)3种工况下2 s内流场流体流动特性进行分析说明。

3 结果分析

3.1 瞬态流场分析

图5为3种工况下调节阀内流场压力云图，可以看出，最大压力为10 MPa，位于入口，最小压力为3 MPa，位于出口。多孔套筒前端流体压力接近于阀前压力，流体流经节流孔时能量损失，流体压力明显下降。图5a中只有内层套筒最下面节流孔处于流通状态，阀内流体的静压在节流孔处产生明显压降。由于小开度流量相对较小，外层套筒降压效果不明显。

图5 压力云图Fig.5 Nephogram of pressure

从图5b和5c可以看出，随着开度增大，流体介质经过各级套筒后均有明显压降。

图6为3种工况下调节阀内流场速度分布云图，可以看出，最大速度均位于多孔套筒处，小开度时流通面积较小，介质的流速较大，内流场最大速度随着开度增加而减小，出口速度随开度增加而提高。

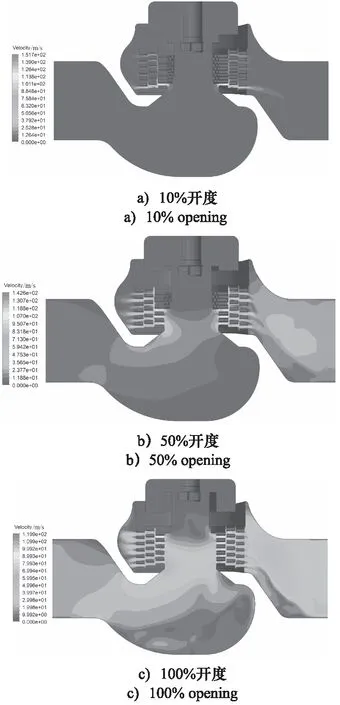
图6 速度云图Fig.6 Nephogram of velocity size

图7为3种工况下调节阀内流场节流套筒处漩涡速度分布云图，可以看出，节流套筒附近存在大量漩涡，且已经形成脱落状态，这种脱落状态会直接影响调节阀工作可靠性，所以对内流场漩涡需具体且细致分析。

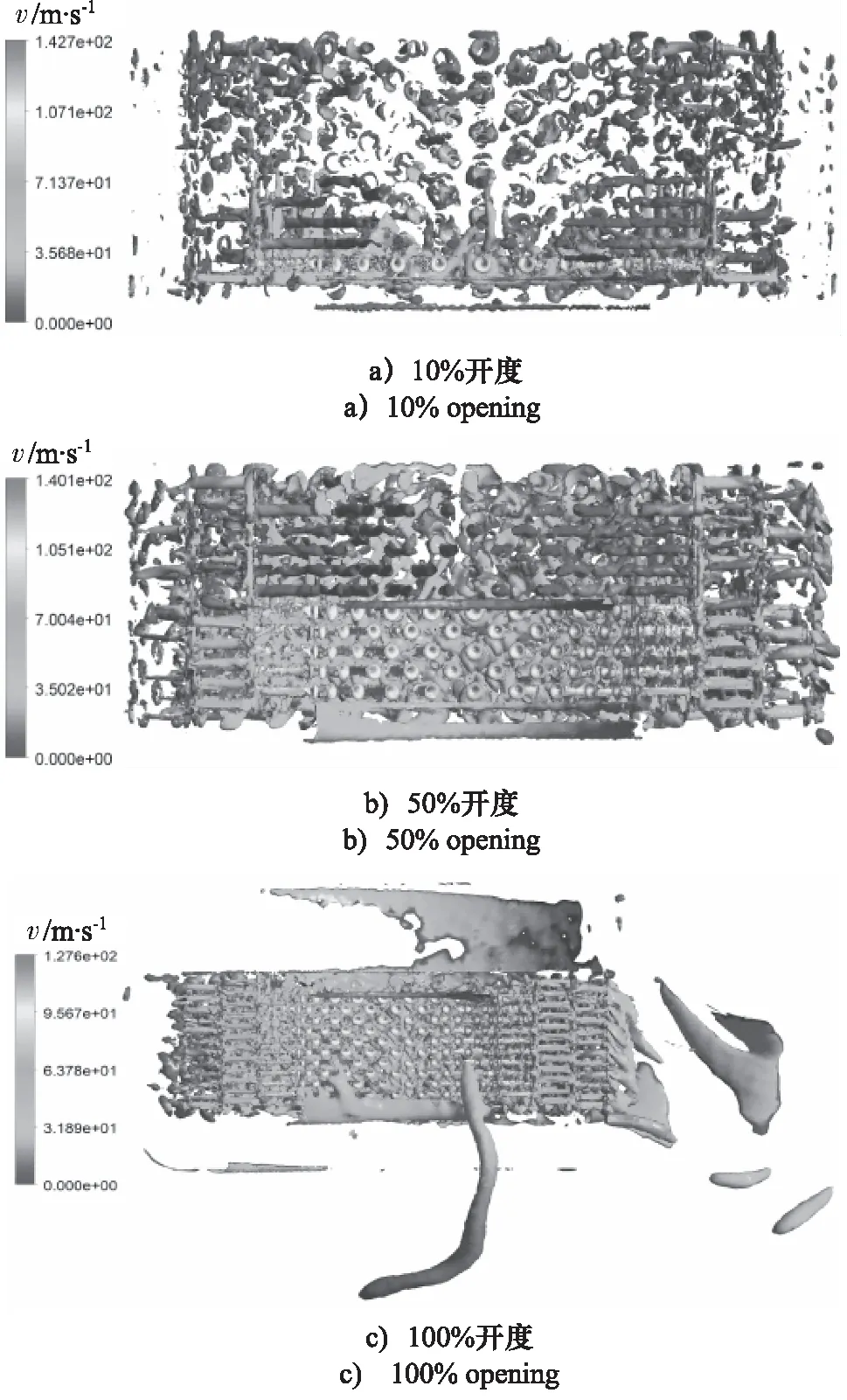
图7 多孔套筒漩涡速度云图Fig.7 Nephogram of vortex velocity at multilayer sleeve

3.2 压力脉动时域频域分析

在调节阀瞬态流场求解过程中，监测各监测点(P1～P9，S1～S4)、监测面(Wall)压力脉动时域信息，之后对时域信息进行快速傅里叶变换， 压力脉动频谱图中峰值点所对应的横坐标即为激振主频[15]。

图8为3种工况下压力脉动时域图。图中监测点P1～P6，S1～S2压力脉动数值为10 MPa左右；P7～P9，S3～S4压力脉动数值为3 MPa左右；10%开度下监测面Wall的压力脉动数值为5.5 MPa左右；50%开度下监测面Wall的压力脉动数值为6.0 MPa左右；100%开度下监测面Wall的压力脉动数值为6.5 MPa左右。10%开度下各监测点压力脉动数值波动不明显；50%开度下P1～P3，S1～S2数值波动幅度不明显，P4～P6存在数值波动，但范围较小，P7～P9，S3～S4数值波动幅度明显；100%开度下P1～P3，S1～S2数值波动幅度较小，P4～P6数值波动幅度明显；P7～P9，S3～S4数值波动幅度剧烈，范围较大。随着调节阀开度的增大，各监测点与监测面压力脉动数值波动范围越来越大，波动越来越剧烈。

图8 不同开度压力脉动时域曲线Fig.8 Time domain curve of pressure pulsation at different opening

分析可知调节阀工作过程中，内流场压力脉动主要集中于阀中后区域。近壁面压力脉动主要集中在出口处，进口压力脉动的范围、剧烈程度均小于出口。调节阀开度增大时，压力脉动有明显增大。

对压力脉动时域特性曲线进行快速傅里叶变换，获得0～2000 Hz相应频域特性曲线。此调节阀在工作过程中产生的压力脉动主要集中在300 Hz以内，压力脉动功率谱密度G如图9所示。

图9 不同开度压力脉动频域曲线Fig.9 Frequency domain curve of pressure pulsationat different opening

3种开度下，监测点P1～P3功率谱密度数据均较小，无主频，原因可能是P1～P3均位于入口处，受高压，会向阀体中部流动，近似层流，故不会产生明显压力脉动与主频；中等50%开度下，监测点P4～P6功率谱密度数值最大，原因可能是这3个监测点位于阀门内部，多孔套筒会对流体产生阻力，且上方存在阀塞与上端盖形成的密封区域，在调节阀中部流体会产生漩涡，影响压力稳定性；全开100%开度下，监测点S4功率谱密度数值最大，原因可能是监测点位于阀门出口下端，经过降压套筒的流体，会对调节阀下端行成冲击力，这是由于调节阀阀体形状引起的，与S3对比，下端的冲击力要大于上端，故调节阀出口下端的压力稳定性小于出口上端。

根据压力脉动时域曲线与频域曲线得出：引起压力脉动的主要因素为调节阀开度与流道形状；不同开度下，介质流经不同的多孔套筒时，流速受到的扰动不同，造成压力脉动也不同，近壁面压力脉动以出口下端最为明显；相比于其他2个开度，100%开度的流激主频多且分布范围广，导致调节阀高开度运行时，更容易产生流激振动。

4 热流固耦合模态分析

在ANSYS Workbench平台下联用流场、温度场、静力场与模态分析模块，流场中计算稳态压力场、温度场；温度场中计算固体温度；静力场进行调节阀的耦合场计算，将计算结果导入模态模块，从而完成预应力模态分析[16-17]。

4.1 固体网格划分与材料参数

调节阀采用ANSYS Meshing软件进行网格划分，并对节流孔处进行局部细化，考虑其对称性与计算成本，故采用半模型。以调节阀全开度下模型为例，其网格如图10所示，调节阀主要零件材料参数如表3所示。

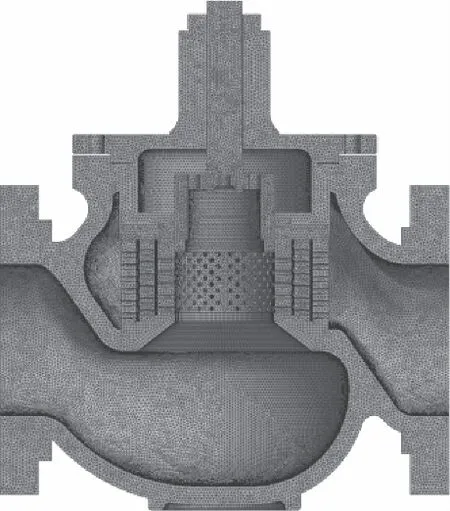
图10 调节阀最大开度网格模型Fig.10 Throttling model grid in max opening of valve

表3 零件材料参数Tab.3 Material preference parameters of parts

静力场中加载耦合面压力信息和调节阀温度信息，并对调节阀进口端施加固定约束，出口端施加位移约束，考虑重力加速度影响。以调节阀最大开度为例说明耦合信息，如图11所示。

图11 调节阀静力场加载信息Fig.11 Static field loading information of valve

4.2 模态频率分析

高阶模态频率和振型可以看作若干个低阶模态和振型的组合，所以计算得到调节阀3种开度下前六阶热流固耦合模态固有频率，如表4所示。

表4 调节阀模态频率Tab.4 Modal frequencies of valve

由表4可知，调节阀开度越大，各阶模态频率均逐渐减小；各开度下随模态阶数的增大，调节阀模态频率均逐渐增大。调节阀的一阶模态频率均大于33 Hz，可以采用等效静力法进行抗震分析[18]。

4.3 模态变形分析

计算得到3种开度下一阶模态振型图如图12所示，并将一阶模态振型的最大值汇总形成表5。

表5 调节阀一阶模态振型最值表Tab.5 Most valve of first-order modal shapes of valve

由图12分析得到，3种开度的最大变形处均位于阀杆末端，最小变形均位于多级降压调节阀入口处，且随着开度增大，第一阶模态的最大变形量在小范围内减小。

山西农村有多美，农村广播告诉你。加大与各地市的联合是“三农”媒体发展的方向，将各地的农业品牌、秀美风光、地方文化通过“三农”媒体进行展示将会更有特色更具影响力。

图12 调节阀一阶振型图Fig.12 First-order mode diagram of valve

通过对压力脉动频域特性曲线与多级降压调节阀的热流固耦合模态频率相比较可知，3种开度下两者均没有相等或接近的频率值，调节阀内流场流体不会发生流激共振，安全性较高。

5 结论

(1) 多级降压调节阀2 s时刻，随着开度增大，多孔套筒降压效果逐渐明显；节流孔处流速逐渐减小；出口流速逐渐增大；多孔套筒处漩涡数量增多、速度减小、尺寸减小，已有脱落迹象;

(2) 压力脉动主要由调节阀开度、流道形状等方面共同引起的，调节阀出口压力脉动剧烈程度大于中部大于入口，调节阀出口下端的近壁面压力脉动最为剧烈;

(3) 由压力脉动频域曲线可知，10%开度下，各监测点、监测面压力脉动主频范围为0～50 Hz； 50%开度下，各监测点、监测面压力脉动主频范围为0～150 Hz；100%开度下，各监测点、监测面压力脉动主频范围为0～180 Hz;

(4) 3种开度下，多级降压调节阀第一阶模态振型最大变形量均出现在阀杆顶端，最小变形量均出现在调节阀进口端，调节阀开度越大，各阶模态频率均逐渐减小；各开度下随模态阶数的增大，调节阀模态频率逐渐增大;

(5) 调节阀3种开度下，压力脉动峰值频率均没有与其固有频率相等或相近，调节阀不会发生流激共振，可靠性较高。