基于铝合金减振器塔的白车身模态分析与研究

唐程光，赵 震，阚洪贵

基于铝合金减振器塔的白车身模态分析与研究

唐程光，赵 震，阚洪贵

（安徽江淮汽车集团股份有限公司技术中心，安徽 合肥 230601）

为了确保白车身模态性能在设计阶段满足要求，在设计前期需要对白车身模态进行分析研究。论文首先利用有限元分析软件对搭载铝合金减振器塔的某钢铝混合白车身设计模型的模态进行仿真分析和摸底，再通过试验测试方法对实车的模态进行分析确认，两种方法相辅相成，为后期的产品优化提供有效数据支撑。结果表明：有限元分析结果精度高（有限元分析结果与试验测试结果基本相当，误差在2%左右），有限元分析软件强大的模拟计算能力使大量繁琐的工程问题简单化，可以节省大量的开发时间和成本；同时再结合试验测试对有限元分析结果进行校核修正，两种方法相结合可以为汽车设计方案的设计和优化提供行之有效的解决方案。

钢铝混合白车身；模态；有限元分析；测试；分析与研究

引言

汽车NVH性能直接关系到整车的舒适性，是提升汽车品质的关键因素，也是近些年汽车行业研究和探索的主要方向之一。白车身模态作为汽车性能的重要评价指标直接影响车辆的NVH性能。白车身模态主要是考虑系统的共振问题，避开发动机、变速器等旋转振动部件的自身频率，避免与其耦合产生共振造成对整车的影响甚至破坏[1]。本文基于搭载铝合金减振器塔的某钢铝混合白车身，利用有限元分析和试验测试两种方法对白车身的模态进行分析，并对两种分析结果进行对比研究，进而为后期的产品优化提供有效数据支撑。

1 有限元仿真分析

1.1 有限元模态分析理论

模态是机械结构的一种固有特性，包括结构的固有频率、阻尼比和振型，有限元模态分析先通过网格划分建立白车身的有限元数学模型，将一般结构系统离散为一种具有多个自由度的线弹性系统，其力学方程为[2]：

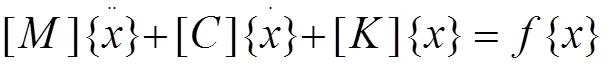
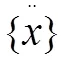
本次有限元模态分析为自由模态分析，无边界条件，可以看作为无阻尼自由振动，因此将公式（1）简化为：

使用拉普拉斯变化可得：

|−2| = 0 （3）

由振动理论可知，自由振动下的弹性结构系统的振动形式可由几个简谐振动相互叠加得到，因此求解可得到简谐振动式（4），进一步得到自由振动下弹性系统的振型及振动频率：

{} = {}sin () （4）

式中{}是振动频率；{}是与时间不相干的位移向量。

([]−2[]) {}= 0 （5）

|[]−2[]|=0 （6）

利用式（6）可得到结构的固有频率，然后再利用式（5）可得到模态阵型，最终得到结构的固有频率和模态振型。

1.2 有限元模型建立

基于压铸铝合金减振器塔的白车身3D数模建立的有限元分析模型如下图1所示，钣金件采用SHELL单元离散，SPR、FDS、粘胶采用SOLID单元模拟，其余缝焊采用REB2单元模拟，点焊采用SOLID单元模拟。分析中使用的软件有ANSA、NASTRAN、HYPERVIEW。

图1 白车身有限元分析模型

表1 材料属性

材料密度弹性模量/MPa泊松比 钣金7.85E−092.10E+050.3 铝合金2.7E−097.2E+040.3 粘胶1.1E−09700.49

1.3 有限元分析边界条件

有限元分析所需要的边界条件：自由模态，无约束、无载荷。

1.4 有限元分析结果

表2列举出典型的模态有限元分析结果，图2为变形云图。

表2 模态有限元分析结果

阶数频率/Hz振型 139.22一阶扭转 249.03一阶弯曲

根据分析计算，由分析结果可以看出：

（1）由分析结果可知，匹配压铸铝合金减振器塔的白车身一阶扭转与原钢质结构基本一致，一阶弯曲略高于原钢质结构。（2）各阶模态均高于目标值，匹配压铸铝合金减振器塔的白车身满足设计要求。

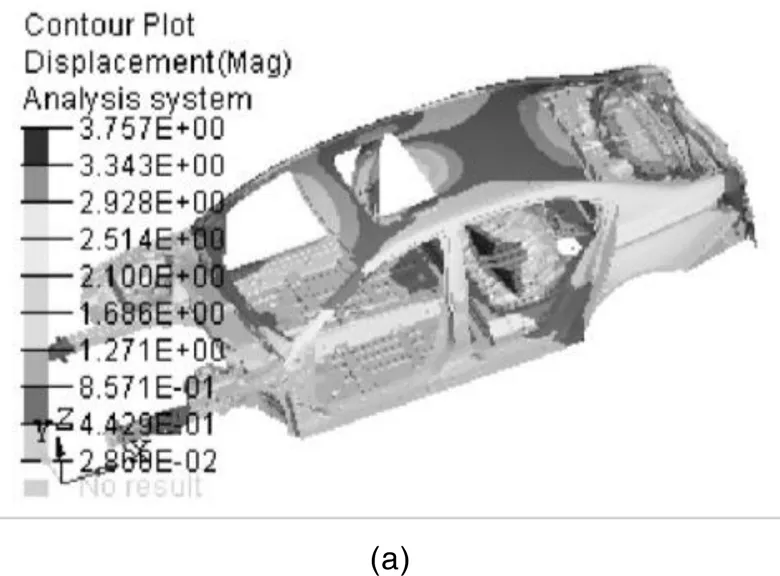
表3 模态对比分析表（有限元分析）

阵型频率/Hz目标值 钢质白车身铝合金减振器塔白车身 一阶扭转39.2239.22＞35 一阶弯曲48.2949.03＞45

2 模态试验测试

2.1 试验方法

在“自由-自由”边界条件下测试白车身模态参数。模态试验包括以下几个主要步骤：

（1）在LMS Test.Lab 软件建立试验文件，安装传感器、连接测试系统、确定测点并建立几何模型，测点选择需满足：测点位置能完全描述白车身形状，布置在车身较平整的位置，相邻测点间距20～30 mm，测点通过直线连接，形成构造面。本试验共布置129个测点，几何模型如图3所示。

图3 白车身及几何模型

（2）白车身模态测试有激振器法和力锤法两种，本试验采用激振器法，车身使用空气弹簧支撑以模拟自由边界条件，激振位置分别位于左前纵梁前端下部和右后纵梁后端下部，如下图4、5所示。

图4 激振位置1（左前纵梁）

图5 激振位置2（右后纵梁）

（3）进行激振试验，并采集激励力与加速度的响应信号。

（4）进行系统参数识别，从测得的输入/输出数据中确定样件的振动特性，通过处理获取频率响应函数（FRF）数据，得到固有频率（Hz）、阻尼比（%）及振型描述。

2.2 试验设备

试验设备如下表4所示：

表4 试验设备

仪器名称规格型号品牌量程/精度 LMS SC3采集器SC310UTP西门子100 mV～10 V/24位ADC精度 三向加速度传感器356A26PCB±100g pk 激振器TV51120TIRA

2.3 试验测试结果

（1）总体频响函数见图6。

图6 总体频响曲线FRF

表5 车身模态频率、阻尼比及振型描述

阶数频率/Hz阻尼比/%振型描述 140.130.29车身一阶扭转模态 249.560.17车身一阶弯曲模态

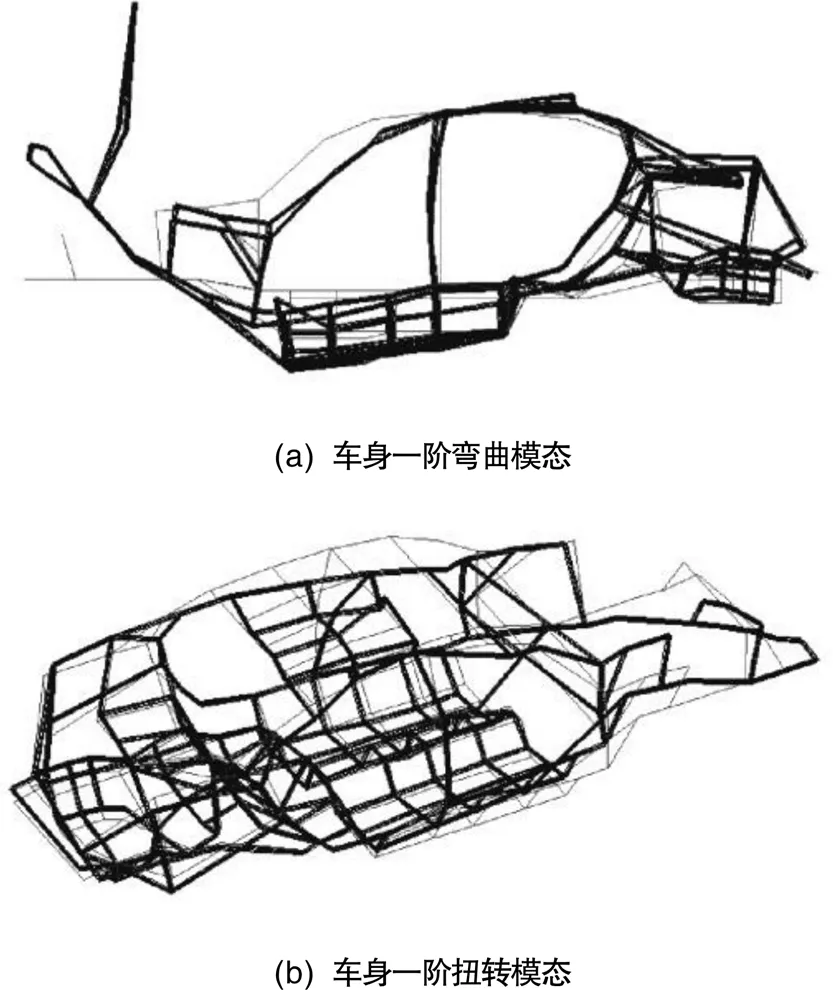
图7 振型图示

白车身典型的模态频率、阻尼比及振型描述见表5、图7所示，一阶扭转模态40.13 Hz，阻尼比0.29；一阶弯曲模态49.56 Hz，阻尼比0.17。

3 结果分析研究

（1）根据下表6结果显示，铝合金减振器塔白车身的一阶扭转、一阶弯曲试验结果与有限元分析结果基本相当，误差在2%左右（有限元分析结果可信度较高）；（2）铝合金减振器塔白车身的一阶扭转与钢质结构基本一致，一阶弯曲略高于钢质结构；（3）铝合金减振器塔白车身各阶模态均高于目标值，满足设计要求。

表6 模态对比分析表

阵型频率/Hz目标值 钢质白车身（有限元分析）铝合金减振器塔白车身（有限元分析）铝合金减振器塔白车身（试验测试） 一阶扭转39.2239.2240.13＞35 一阶弯曲48.2949.0349.56＞45

4 结语

本文基于搭载铝合金减振器塔的某钢铝混合白车身，利用有限元分析和试验测试两种方法对白车身的模态进行分析，其中有限元分析软件强大的模拟计算能力使大量繁琐的工程问题简单化，可以节省大量的开发时间和成本；同时再结合试验测试对有限元分析结果进行校核修正，两种方法相结合可以为汽车设计方案的设计和优化提供行之有效的解决方案。

[1] 李旭伟,杨东绩,田程.一种白车身车顶模态和动刚度测试分析方法的研究[J].时代汽车,2019(10):84-86.

[2] 王书贤,薛栋,陈世淋,等.基于HyperMesh的某轿车白车身模态和刚度分析[J].重庆理工大学学报(自然科学),2019,33 (07):50-57.

Modal Analysis and Research of BIW Based on Aluminum Alloy Shock Absorber Tower

TANG Chengguang, ZHAO Zhen, KAN Honggui

( JAC Technical Center, Anhui Hefei 230601 )

In order to ensure that the modal performance of BIW meets the requirements in the design stage, it is necessary to analyze and study BIW modal in the early stage of design. Firstly, the modal of a steel-aluminum hybrid BIW design model equipped with aluminum alloy shock absorber tower is simulated and analyzed by finite element analysis software, and then the modal of the real vehicle is analyzed and confirmed by test method. The two methods complement each other and provide effective data support for later product optimization. The results show that the accuracy of finite element analysis results is high (the results of finite element analysis are basically the same as the test results, and the error is about 2%). The powerful simulation and calculation ability of finite element analysis software simplifies a large number of tedious engineering problems, which can save a lot of development time and cost. At the same time, the results of finite element analysis are checked and corrected by test. The combination of the two methods can provide an effective solution for the design and optimization of automobile design scheme.

Steel-aluminum hybrid body-in-white; Modal; Finite element analysis; Test; Analysis and research

U463.33+5.1

A

1671-7988(2022)02-57-04

U463.33+5.1

A

1671-7988(2022)02-57-04

10.16638/j.cnki.1671-7988.2022.002.014

唐程光（1977—），男，湖南邵阳人，科技部重大专项评审专家，博士，安徽江淮汽车集团股份有限公司总经理助理，从事汽车整车、车身、电子部件和产品造型的设计开发工作。