三峡库区仙女山断裂周缘地震类型特征识别
2022-02-21徐玉聪朱建董建辉周鲁
徐玉聪 朱建 董建辉 周鲁


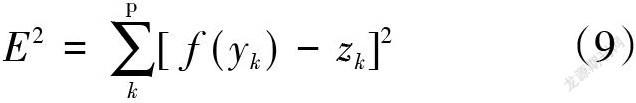

摘要:为识别仙女山断裂周缘发生的构造地震、矿震、塌陷地震特征,基于集合经验模态分解时频分析方法(EEMD)对地震波形信号进行了分解,通过信号的IMF分量的时频谱和边际谱分析了其差异。结果表明:① 构造地震的时频谱频率在0~40 Hz均有分布,频率成分复杂,边际谱集中在0~20 Hz;② 矿震时频谱在0~30 Hz均有分布,频率成分相对简单,但在地震波幅值变化最大的区域存在20~30 Hz的频率成分空白区,边际谱存在一个0~5 Hz的主频带和2 Hz左右的主频;③ 塌陷地震时频谱频率成分分布在0~30 Hz,在Pg波到达前存在0~5 Hz左右低频区域,边际谱的主频带和主频集中在0~3 Hz和1 Hz。该研究成果可以作为识别构造、矿震、塌陷地震事件的判别依据。
关键词:EEMD; 仙女山断裂; 时频分析; 边际谱; 三峡水库
中图法分类号:P315 文献标志码:A DOI:10.15974/j.cnki.slsdkb.2022.02.002
文章編号:1006 - 0081(2022)02 - 0009 - 08
0 引 言
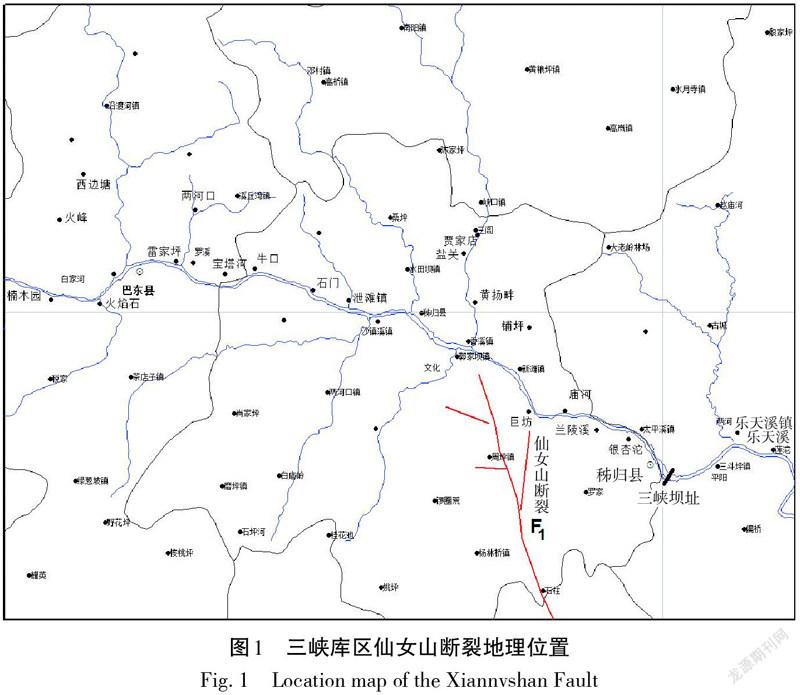
仙女山断裂是三峡库区的主要断裂带之一,位置如图1所示,位于黄陵地块西南侧,北起秭归荒口以北的风吹垭,南止于五峰渔洋关,全长80余千米,距三峡坝址最近处约19 km。自从三峡水库蓄水后,仙女山断裂周缘发生了大量的微小地震活动,大致可以分为构造地震、矿震、塌陷地震。有效识别这些微小地震类型对于仙女山断裂附近的地震活动特征和趋势研究具有重要意义。
国内外研究人员针对不同地震类型地震波的时频谱特征识别开展了大量的研究工作,其中主要集中在短时傅里叶变换(STFT)[1-2]、小波变换(WT)[3-5]、戈勃(Gabor)展开、维格纳-威尔分布(Wigner-Ville)[6]等。虽然上述时频分析方法在应用中取得了一定成果,但是这些方法本身也存在一些局限性,主要由于以下几种原因造成:这些方法都基于线性理论、需选取不同时窗、需引入交叉项或者依赖于前验的基函数等,而地震波作为一种非线性、非平稳的随机信号,需要依赖于信号自身非线性、非平稳的特点进行分析计算,因此,合适的时频谱分析方法对于分析研究结果也会产生较大影响。
希尔伯特-黄变换(Hilbert-Huang,HHT)作为一种非线性、非平稳信号的处理方法,通过经验模态分解(Empirical Mode Decomposition,EMD) [7],可基于信号自身特点,将复杂地震信号自适应地分解为一系列固有模态函数(Intrinsic Mode Function,IMF),通过对每个IMF分量进行Hilbert变换,可以准确获取反映信号时频特征的瞬时频率和振幅、边际谱等结果,目前在地震分析、机械诊断等信号处理中得到了广泛应用[8-11]。
本文利用基于集合经验模态分解算法(EEMD)的HHT算法,对仙女山断裂周缘的构造、矿震、塌陷地震的波形特征进行了系统的分析,从时频分布和边际谱分布两方面提出3种地震的判别依据。
1 理论和方法
HHT时频分析方法由经验模态分解和希尔伯特变换组成,具有能够稳定、自适应地处理非线性和非平稳信号的特点。其中本文采用的集合经验模态分解算法(Ensemble Empirical Mode Decomposition,EEMD)是对Huang提出的EMD方法的优化改进[12]。该方法主要原理是在原始数据中加入白噪声,以此补充EMD分解过程中尺度不足的问题;不同时间尺度的信号可以自动分离到与其相适应的参考尺度上去,从而有效改进EMD分解过程中的模态混叠现象,得到一系列的IMF和趋势项。此外,该方法同时保留了EMD方法简单高效处理非线性、非平稳信号的特点;每个IMF分量经过Hilbert变换,可以获取信号的瞬时频率和振幅、边际谱等数据。
1.1 EEMD和希尔伯特变换
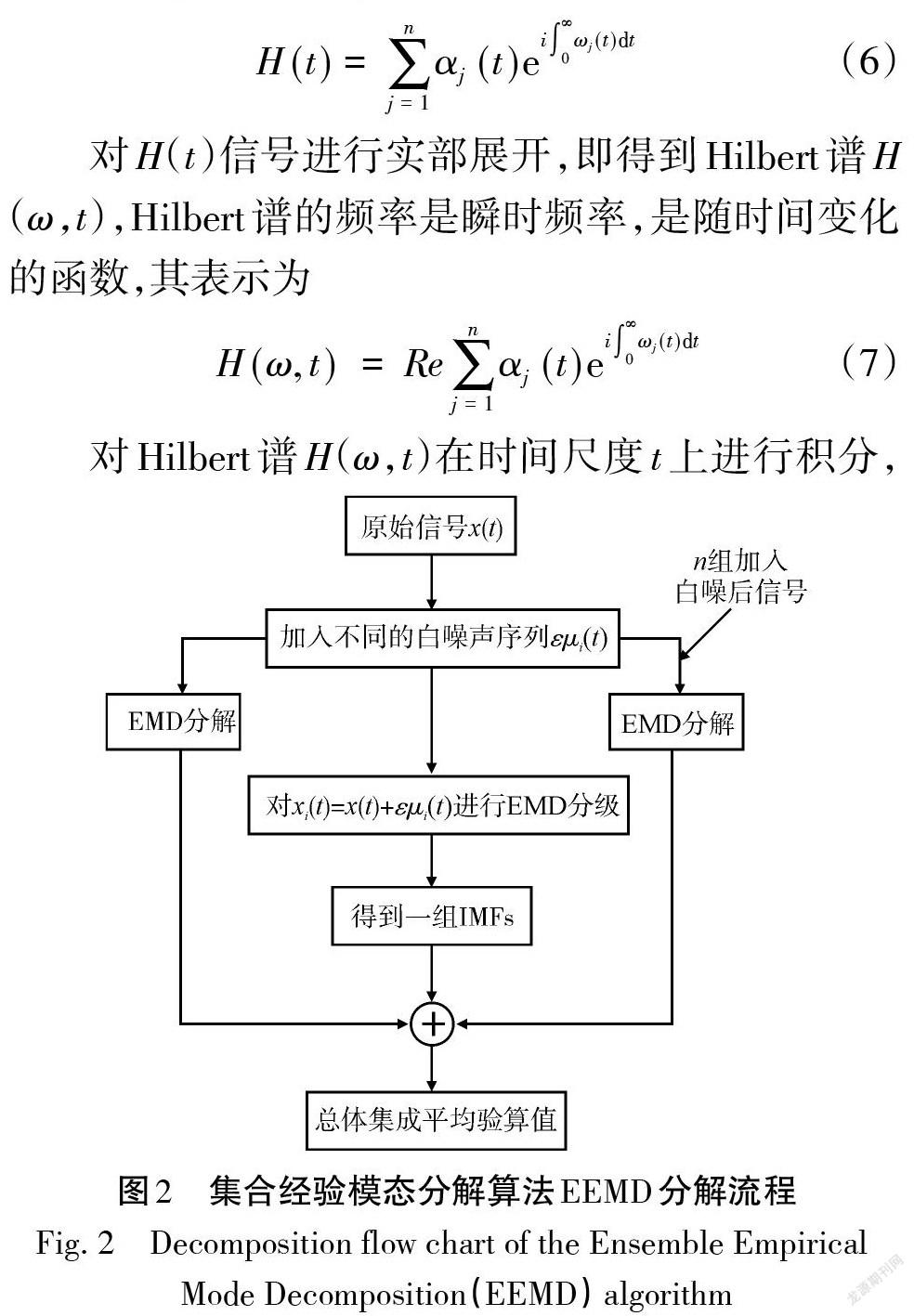
在进行Hilbert变换之前首先对信号进行EEMD分解,其中集合经验模态分解算法(EEMD)的分解流程如图2所示,具体步骤包括:
(1) 将正态分布的白噪声加到原始信号x(t);
(2) 将加入白噪声εμi(t)的信号作为一个整体,进行EMD分解,得到各IMF分量cij(t);
(3) 重复步骤(1)和(2),每次加入新的正态分布白噪声序列;
(4) 将每次得到的IMF分量cij(t)做集成平均处理后作为最终结果。
各个单分量IMF信号cj(t)由经过经验模态分解后不同时间尺度的信号组成,且最终分解结果还包含一个信号趋势项r(t)。具体实现步骤如下。
式中:x(t)代表原始信号;εμi(t)代表加入的白噪声信号,其中ε代表加入白噪声的噪声水平;xi(t)是加入噪声后的信号,i=1,2,…,n。
对加入白噪声后的信号xi(t)进行EMD分解,得到m个IMF分量cij(t)和趋势项ri(t),其中j=1,2,…,m,如式(2)所示:
最后通过集合平均,分别得到原始信号x(t)的分解结果cj(t)和趋势项r(t),如式(3)~(5)所示。
通过EEMD分解得到一系列单分量IMF信号之后,对各个IMF分量进行信号的Hilbert变换,得到H(t),如式(6)所示,其中αj为第j个IMF的单分量信号的幅值,ω为角频率。
对H(t)信号进行实部展开,即得到Hilbert谱H(ω,t),Hilbert谱的频率是瞬时频率,是随时间变化的函数,其表示为
对Hilbert谱H(ω,t)在时间尺度t上进行积分,如式(8)所示,可以计算得到Hilbert边际谱h(ω),其幅值可以真实地反应频率在信号中是否存在[13],并且可以精细地表示信号幅值在整个频率段上随频率的变化情况。
1.2 最小二乘算法
最小二乘法的基本理论是:给定数据集{(yk, zk)}(k=0,1,2,…,p),求取合适的函数f(y),使误差的平方和E2最小,其中E2由下面公式(9)得到,其主要数学意义即把拟合值和观察值之间的最小化距离平方和作为目标来优化。
通过最小二乘法得到拟合函数f(y),可以有效表征原始数据集的变化趋势和变化特征。
2 数据选取
为了最大限度减小地震波在传播过程中受到介质、几何扩散、频散和仪器等因素的影响[14],尽量选取同一地震台记录到的地震事件,同时考虑到矿震的震级大部分较小,所以针对构造、矿震、塌陷地震均选取ML 2.0~3.0级左右地震进行分析。
基于上述原则,选取发生于2007~2016年之间的仙女山断裂南麓周坪地震台的数字化观测波形事件作为研究对象,其中构造、矿震、塌陷地震事件各10次,相关地震资料已经过地震波资料分析和现场实地考察确认,震中位置和周坪地震台距离Δ≤15 km,震级分布于ML 2.0~3.0级之间,采样频率100 Hz,频带范围0~40 Hz。
依据地震事件的发震时刻,所有事件选取三分向中垂直向波形数据,截取P波到时前1~2 s作为波形分析的开始,数值均采用未经过电压转换的counts值,利用python脚本程序对原始的波形数据进行处理,去除仪器响应部分,并进行去均值和去倾斜校正,然后选取30 s左右的时长进行分析,选取的数据充分包含了地震波形的震荡和衰减信息。
3 频谱特征分析
3.1 时频分析
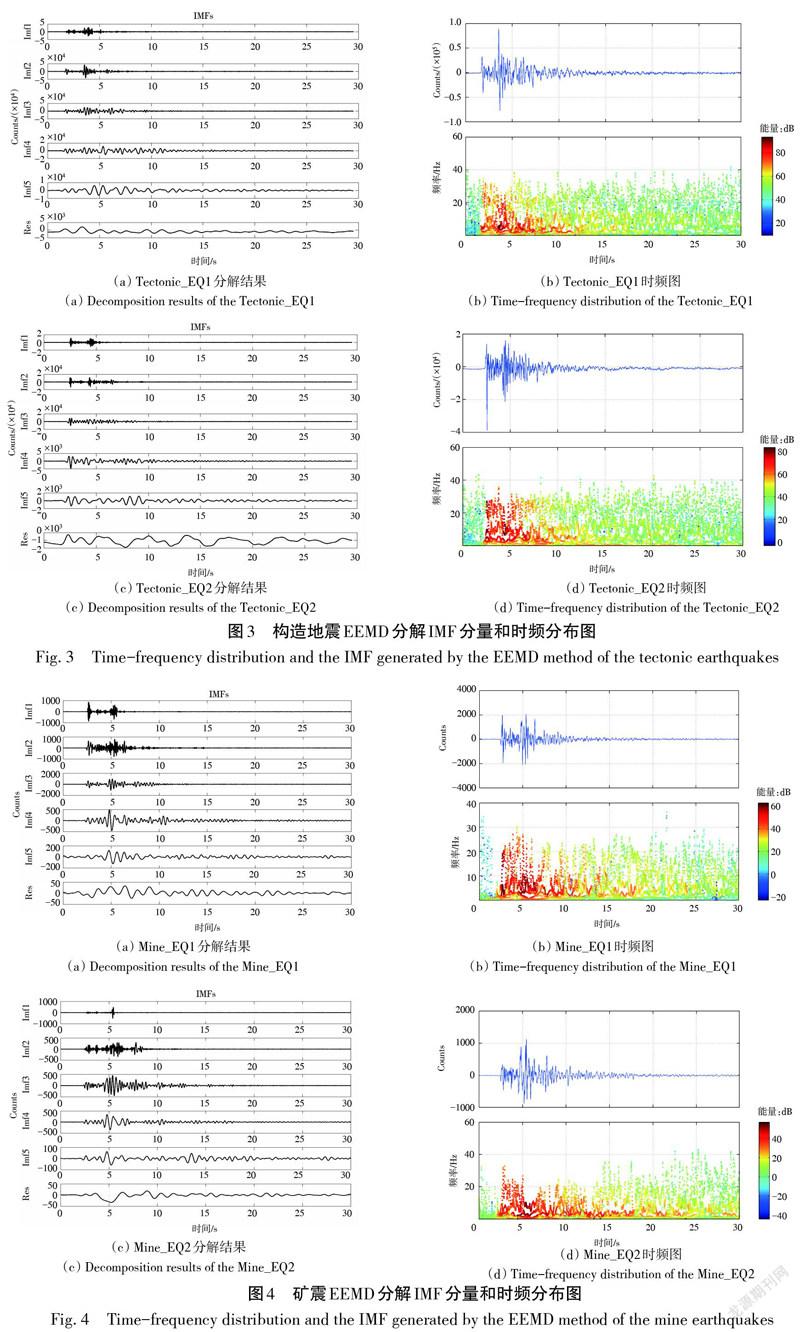
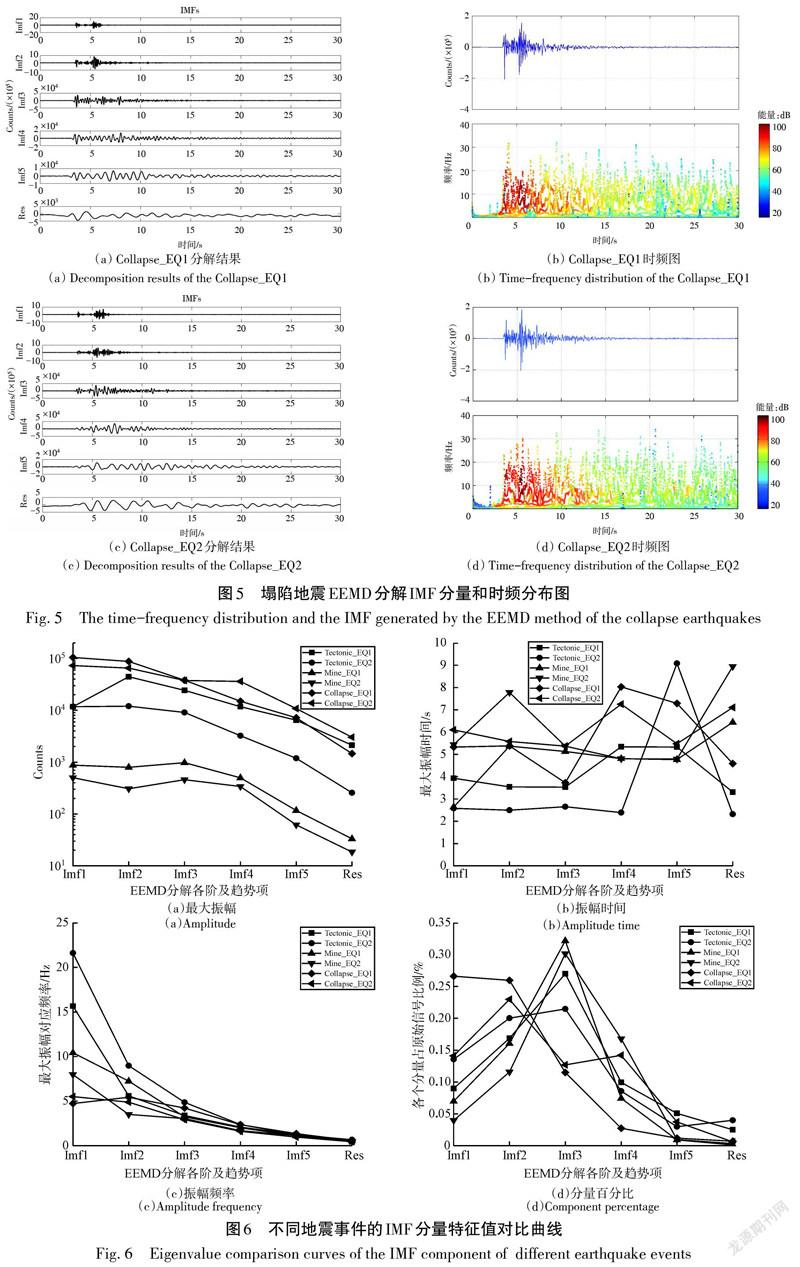
本文对10次构造地震、矿震、塌陷地震事件的EEMD分解和Hilbert时频图谱进行了计算分析,时频图谱主要反映频率成分随时间的变化特征,这里仅选取3种地震各2次事件做详细说明。其中构造地震事件1(Tectonic_EQ1),震级为ML 2.1级,EEMD分解结果和时频图如图3(a)~(b)所示,构造地震事件2(Tectonic_EQ2),震级为ML 2.0级,EEMD分解结果和时频图如图3(c)~(d)所示;矿震事件1(Mine_EQ1),震级为ML 2.2级,EEMD分解结果和时频图如图4(a)~(b)所示,矿震事件2(Mine_EQ2),震级为ML 2.1级,EEMD分解结果和时频图如图4(c)~(d)所示;塌陷地震事件1(Collapse_EQ1),震级为ML 2.6级,EEMD分解结果和时频图如图5(a)~(b)所示,塌陷地震事件2(Collapse_EQ2),震级为ML 2.8级,EEMD分解结果和时频图如图5(c)~(d)所示。上图中,Imf1~5代表1~5阶IMF分量,Res代表残差。
通过对比分析3种类型地震事件的原始波曲线可知,波形曲线差异比较大,对于不同地震事件类型,Pg波到达后均有明显的不同跳变出现,这和不同的发震因素有关;同种类型的地震事件, Pg波初至之后其波形的形态基本一致。不同地震事件分解后各IMF分量的特征如图6所示,其中对于相同类型地震事件,其IMF分量的最大振幅曲线走势基本一致;最大振幅对应时间和各个分量占原始信号的百分比因发震因素不同而规律性不明显,但是不同地震事件Imf1最大振幅对应的频率差别明显:构造地震事件频率分布在15~25 Hz之间,矿震事件频率分布在5~15 Hz之间,塌陷事件频率分布在5 Hz左右。该分析结果也说明了不同地震事件类型在频率特征上存在明显差异。
3种地震类型的EEMD分解结果均按照原始数据的尺度,根据高频到低频的顺序分解出了IMF分量。同种地震类型的EEMD分解结果曲线形态是一致的,这是因为在分解过程中加入了白噪声,同时这也避免了计算Hilbert谱过程中的模态混叠现象。
分析以上3种类型地震的时频分布图,Pg波到达之前的时频谱具有如下特征:① 构造地震在Pg波到达之前随着时间变化出现了能量较低但频带较宽、成分复杂的频率,并且一致延伸到Pg波到达;② 矿震在Pg波到达之前,随着时间推移,出现了能量较低但频带较窄、成分简单的频率,并且在Pg波到达之前有一个不规则的低频带区域;③塌陷地震在Pg波到达之前,只存在极低频率成分的频带区。
进一步分析Pg波到达之后的时频谱,构造地震在地震波增大和衰减的过程中,0~40 Hz的频率成分均有分布;矿震在地震波增大和衰减的过程中,0~30 Hz的频率成分也均有分布,但是在地震波幅值变换最大的区域,20~30 Hz频率成分出现了空白区;塌陷地震在地震波增大和衰减的过程中,频率成分主要集中在0~30 Hz。
通过分析仙女山断裂周缘3种地震的时频图分得出,在Pg波到达前后,不同地震类型的频谱存在明显差异,主要是因为发震原因的不同:①构造地震由地壳介质中岩石破裂引起,是岩层中应力从积累到释放的过程,其震源机制较为复杂,因而地震波频率成分复杂,能量释放缓慢,震动持续时间较长,这与分析的构造地震频带宽、频率成分分布均匀是一致的;②矿震是人工震源,震源较浅,震动幅值大,能量衰减快,传播介质疏松,高频成分易被吸收,所以时频谱图在最大震动幅值前后出现了高频成分的空白区;③塌陷地震是由于塌陷体坠落撞击底部岩体而导致的瞬时压缩源,其地震波傳播路径简单,从图5(b), (d)的时频谱图分析可知,与构造地震和矿震相比,塌陷地震的频带范围窄、高频成分少。
3.2 边际谱分析
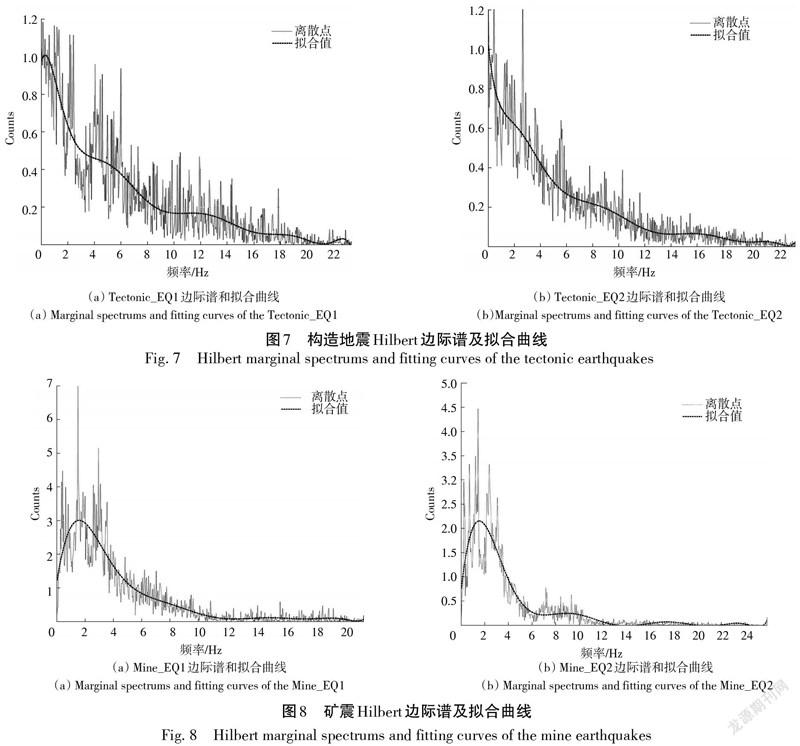
采用公式(8)中的计算方法,对3.1节中详细分析的构造地震、矿震、塌陷地震各10次事件进行计算得到原始地震信号的边际谱,并采用公式(9)对边际谱的计算结果做最小二乘拟合。选取与3.1节中进行时频分析的6次事件相对应的计算结果进行如下分析说明。
图7是两次构造地震的边际谱及拟合曲线,从图中可以直观看到边际谱集中在0~20 Hz的范围,拟合曲线呈现出逐渐下降的趋势,这与构造地震能量缓慢释放的原因是一致的。矿震事件的边际谱及拟合曲线如图8所示,矿震有一个明显的主频带,集中在0~5 Hz,并且存在一个2 Hz左右的主频。分析图9所示塌陷地震的边际谱可知,塌陷地震也存在一个主频带,集中在0~3 Hz,主频略低于矿震,在1 Hz左右。上述3种地震的边际谱,其频带分布和主频均存在明显差异,主要由于不同地震类型的发震因素和传播路径不同引起,而边际谱分析结果准确地反映出了不同地震类型的差异,所以上述边际谱分布特点可以作为识别仙女山断裂周缘3种地震类型的重要依据。
4 结 论
通过基于EEMD的HHT时频谱和边际谱算法,对三峡库区周坪地震台记录到的仙女山断裂周缘大量的构造、矿震、塌陷地震波形的时频谱和边际谱进行分析,发现3种地震类型的时频分布和边际谱特征存在明显差异,并且主要集中以下几个方面。
(1)在Pg波到达之前,从时频谱分析,构造地震的频带较宽,频率在0~40 Hz均有分布,并且频率成分复杂;矿震的频带较窄,基本分布在频率0~30 Hz之间,频率成分相对简单;而塌陷地震频带极窄,分布在0~5 Hz间,频率成分集中在低频区域。
(2)从时频谱分析Pg波到达后至地震波衰减的时频分布可知,构造地震和矿震在0~40 Hz均有频率成分分布,但是矿震在地震波幅值变化最大的区域出现了20~30 Hz频率成分空白区,这是构造地震和矿震时频分布的主要差异;而塌陷地震的频率成分仅分布在0~30 Hz。
(3)从边际谱拟合结果分析发现,构造地震边际谱集中在0~20 Hz,边际谱曲线在空间上呈现逐渐下降的趋势;矿震的边际谱存在一个0~5 Hz的主频带和2 Hz左右的主频;而塌陷地震的主频带和主频低于矿震,集中在0~3 Hz和1 Hz;三者的边际谱拟合结果存在明显差异。
本文利用EEMD方法对三峡库区仙女山断裂周缘的构造、矿震、塌陷地震事件波形信号进行分解,得到不同时间尺度信号的时频特征和边际谱,并基于上述计算结果,系统地分析和总结了该区域构造、矿震、塌陷地震事件的规律。该研究方法可以作为识别其他研究区域构造、矿震、塌陷地震事件的判别依据,帮助地震分析人员对实时记录的地震波形进行快速识别、分类,进而提高数据分析处理的精度和效率,为抗震救灾提供技术支撑;同时,该方法也可以应用于堰塞湖、滑坡、泥石流等灾害过程所产生地震动信号的处理和分析,能够与其他研究手段相结合,最终实现灾害过程的重构,进而有效指导地质灾害的监测预警和快速评估工作。
参考文献:
[1] 崔鑫,许力生,许忠雄,等. 小地震与人工爆破记录的时频分析[J]. 地震工程学报,2016,38(1):72-77.
[2] 靳玉贞,林木金,范晓瑜,等. 山西地区爆破、塌陷(矿震)特殊地震动特征识别[J]. 地震地磁观测与研究,2015,36(3): 64-66.
[3] 毛世榕,管振德,阎春恒. 基于小波包分形和神经网络的地震与岩溶塌陷识别[J].地震学报,2018,40(2): 195-204.
[4] 曾宪伟,赵为明,盛菊琴,等.应用小波包识别宁夏及邻区的地震和爆破[J].地震研究,2008(2): 142-148,198.
[5] 黄汉明,边银菊,卢世军,等.天然地震与人工爆破的波形小波特征研究[J].地震学报,2010,32(3):270-276.
[6] SANJIT K, DASH G, SASIBHUSAN R, Arrhythmia detection using Wigner-Ville distribution based neural network[J]. IEEE Transaction on Information, 2016, 85(5): 806-811.
[7] HUANG N E, SHEN Z, LONG S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of the Royal Society of London, 2003, 4510(2037): 2317-2345.
[8] CHEN Y, ZHANG G, GAN S, et al. Enhancing seismic reflections using empirical mode decomposition in the flattened domain[J].Journal of Applied Geophysics, 2015, 56(71): 99-105.
[9] LI H, LI Z, MO W. A time varying filter Empirical Mode Decomposition[J]. Signal Processing,2017,138(12): 146-158.
[10] JAN N Y, YING L, HUANG N E, et al. System identification of linear structures based on Hilbert-Huang spectral analysis. Part 1:normal modes[J]. Earthquake Engineering & Structural Dynamics,2016,87(32): 1443-1467.
[11] 楊培杰,印兴耀,张广智. 希尔伯特-黄变换地震信号时频分析与属性提取[J]. 地球物理学进展, 2007, 22(5): 1585-1590.
[12] WANG Y H, YEH C H, Young H W V, etc. On the computational complexity of the empirical mode decomposition algorithm[J]. Physica A,2014(400):159-167.
[13] 钟佑明,秦树人,汤宝平. 希尔伯特-黄变换中边际谱研究[J]. 系统工程与电子技术,2004,26(9):1324-1326.
[14] 张帆,朱新运,熊丹,等.基于非线性时频分析的地震和爆破识别[J]. 华南地震,2014,34(2):56-63.
(编辑:高小雲)
