基于滑动窗口-变分模态分解的深度学习金融时序预测
2022-02-20江嘉华徐鹏程邓小毛
江嘉华 徐鹏程 邓小毛


摘要:针对金融数据的时序特征,构造了滑动窗口-变分模态分解(SW-VMD) 的数据处理方法,对股指收盘价以及收益率时序数据进行分解与重构,把非线性、非平稳的数据序列转换为线性且平稳的数据。处理后的数据作为长短时记忆神经网络(LSTM) 的输入数据,对股票指数未来的收盘价和收益率进行预测分析。实证分析将趋势准确率作为模型的评价指标,以此反映模型对隔天收盘价和收益率涨跌的预测能力。结果显示,与无数据分解的模型相比较,采用了数据分解后的LSTM模型在趋势预测准确率上有显著的优化效果。
关键词:滑动窗口;变分模态分解;长短时记忆神经网络;金融时序预测
中图分类号:TP183 文献标识码:A
文章编号:1009-3044(2022)34-0014-05
1 概述
金融时序预测指根据历史数据建立时间序列等计量模型对各个重要的金融数据指标包括价格、指数、收益率、波动率等进行预测。金融时序数据预测可以更好地认识和理解金融市场的波动规律,帮助国家对金融市场进行风险控制,以及帮助广大投资者利用有效的市场波动信息,做出更加合理的投资策略。金融时序预测的经典方法主要使用ARCH(Autoregressive Conditional Heteroskedasticity Model) 、GARCH(Generalized-ARCH) 等统计模型及其改进模型,描述了金融市场时间序列波动率的异方差性和聚集性的特征[1-2]。21世纪迈入了深度学习的时代,深度学习有许多经典的神经网络模型,比如深度卷积神经网络(CNN) 、深度置信网络(DBN) 、自编码器(AE) 、深度循环神经网络(RNN) 等,其中非常有效处理时序数据的神经网络为长短时记忆神经网络(Long Short-Term Memory, LSTM) 。1997年Sepp Hochreiter和Jurgen Schmidhuber提出长短时记忆神经网络[3]。LSTM神经网络作为循环神经网络(RNN) 的一种,可以有效地提取时序数据中的长期相关性,把远期的有用历史信息保留在神经元中,解决了长期依赖的问题,得到了广泛应用。如在金融时序预测方面,金雪军(2016) 在研究中国通货膨胀水平是否受美国修整货币政策为扩张状态影响时,使用了LSTM进行研究,同时建立了VAR(Value at Risk) 模型进行对比验证,得出结论LSTM模型在经济分析中的表现较之VAR模型更为优秀[4]。谢合亮等(2018) 构建了LSTM期权定价模型,并利用50ETF看涨期权和看跌期权进行实证分析,实验结果表明LSTM期权定价模型比经典的Black-Scholes蒙特卡洛方法具有更高的定价精确性[5]。李莹和王璐璐(2020) 提出了一种基于遗传算法优化的长短时记忆神经网络模型(GA-LSTM) [6],该模型在LSTM的基础上使用了遗传算法对参数进行寻优,针对期货市场价格的复杂、非线性时间序列数据进行了建模预测,通过结果分析发现,价格预测的精度有所提高。陈琪琪(2020) 通过卷积神经网络进行数据的空间结构特征提取,然后使用LSTM对输入的时间序列进行特征提取,使混合了卷积神经网络和長短时记忆网络的CNN-LSTM模型更加有效地预测出短期的当日股票最高价[7]。
处理良好的数据集将使得计算模型的性能显著提升。针对时间序列数据的有效数据分解方法包括经验模态分解(Empirical Mode Decomposition, EMD) [8]及变分模态分解(Variational Mode Decomposition, VMD) [9]等,这些数据分解方法最初被提出并应用于工程信号处理中的降噪问题,随后被推广应用至原油价格[10]、黄金价格[11]等金融数据序列的处理和预测中。其中VMD是新近提出的一种自适应信号分解技术,它基于变分原理,通过求解使得每个模态的带宽之和最小的最优化问题,将多分量信号分解为多个准正交本征模函数。该方法在模中没有残余噪声,并且可以减少冗余模式。在实际金融市场中,由于金融时序数据序列非线性非平稳的特征,对价格、收益率等指标的预测如果直接使用历史收盘价和收益率等数据代入LSTM网络,预测结果往往会出现一定的滞后性,这就导致LSTM对金融指标的涨跌趋势预测准确率较低。本文将提出一种基于滑动窗口的变分模态分解(Sliding Window-Variational Mode Decomposition , SW-VMD) 对中国证券市场股指数据进行处理,提取数据的主要特征后使用LSTM神经网络进行股指价格及收益率涨跌趋势预测,最后设计比较实验验证该模型的有效性。
2 基于SW-VMD数据分解的LSTM神经网络
首先,构建滑动窗口的VMD数据分解算法和LSTM长短时记忆神经网络,然后结合数据分解预处理及该神经网络,分别得到股指收盘价以及收益率的预测模型。
2.1 滑动窗口-变分模态分解算法
VMD算法的核心思路是将原始数据序列的分解问题转化为一个搜索约束变分模型最优解的问题,在满足各个本征模态函数IMF(Intrinsic Mode Function) 与残差函数之和等于原始数据序列的前提下,求解每一个模态的估计带宽的最小值。根据上述条件确定每个分解序列的频率中心以及带宽,从而可以自适应地实现信号的频域剖分以及各分解序列的有效分离,进而提取出多个本征模态函数。在迭代搜寻的过程中,IMF的中心频率和本征模态函数会不断更新,最后分解为多个IMF,以达到信号分解的效果,其中IMF的数量是人为预设的。
对于本文中的金融时序数据,由于VMD每个分解结果都受到全体原始信号的影响,意味着若将整个时间序列数据进行VMD分解,则当前时刻数据的分解结果包含了未来时刻数据的信息,从而无法基于当前时刻的数据分解结果进行预测分析。为了得到对时序输入数据合理的分解和重构结果,本文提出基于滑动窗口的VMD数据分解模式,即以32天为一个数据集长度,采用递进的方式进行数据分解。具体流程如下:第1天至第32天的数据进行VMD数据分解,得到第1天至第32天的数据分解结果,取第32天的数据分解结果存放为模型输入变量的第一个数据,以此数据来预测第33天的收盘价和收益率。如此类推,也即运用第n-31天至第n天的数据分解结果,取第n天的数据存放为模型输入变量的第n-31个数据,以此数据来预测第n+1天的收盘价和收益率。滑动窗口-变分模态分解数据构造流程如图1所示。
图1中VMD_i(i=1,...,n-31) 代表对第i组数据进行变分模态分解;VMD_i_j(i=1,...,n-31,j=i,...,i+31) 表示从第i次变分模态分解得到的第j天的数据分解结果;VMDi则表示输入变量中的第i天的输入数据,为原始数据的第i次变分模态分解结果中的最后一项,即图1中的VMD32=VMD_1_32,VMD33=VMD_2_33,VMD34=VMD_3_34,依此类推VMDn=VMD_(n-31)_(n)。
2.2 LSTM网络结构
长短时记忆神经网络(LSTM) 由输入层、输出层和隐藏层三个部分构成,其中隐藏层的层数和每一层神经元个数决定了神经网络的深度和复杂程度。与生物神经网络相仿,神经元也是神经网络模型中具备运算能力的最小结构单元,LSTM通过神经元让序列信息有选择性地影响神经网络中每个训练步的状态,并使用tanh、sigmoid、ReLU等激活函数输出一个0到1之间的数值作为门控,描述当前输入有多少信息量可以通过这个“门”。而“层”就是神经元的集合,各个层以一定的方式互相连接就构成了神经网络。LSTM算法主要包括前向传播和反向传播两个过程,前向传播按遗忘门、输入门、输出门的顺序处理信息;反向传播则是利用链式法则计算每个神经元中的权重和偏置梯度;最后使用优化算法反复更新这些系数,直至训练出适合该问题的神经网络模型。图2为LSTM单元结构示意图。
从LSTM单元结构可以看出,该神经网络不仅可以从序列当前数据状态中提取有用信息,还能保留距离当前状态较远的计算步中具有长期相关性的信息,所以LSTM是解决时序问题的理想工具之一。综上,基于SW-VMD数据分解的LSTM时序预测模型的具体算法流程如下:
step1: 对长度为n的股指收盘价序列以及收益率序列,进行滑动窗口-变分模态分解,得到长度为n-31,本征模函数IMF数量为m的数据作为模型的输入变量;
step2: 将数据分割为训练集、验证集以及测试集,其中验证集长度为30天,测试集长度为60天;
step3: 在模型训练的過程中,在训练步数达到1000步后开始引入验证集,每30步验证一次获取各个模型的验证集结果,并保存训练过程中验证集表现较好的模型;
step4: 对训练结束后保存下来的模型输入测试集数据进行股指收盘价以及收益率预测,验证并比较不同模型以及数据对预测性能的影响。
3 实证分析
由于股票指数具有较强的股票市场代表性,作为投资对象相对稳健,本文选取上证指数、沪深300的股指收盘价以及收益率数据,运用当前时间之前的历史信息,构建LSTM神经网络模型预测隔天的股指收盘价和收益率的涨跌趋势。 本文使用波动较小的收盘价以及波动较大的收益率两种数据进行数据分解,以此验证算法对两种波动性差异较大数据的作用,构建价格预测模型以及收益率预测模型。同时本文将无数据分解的模型与使用SW-VMD数据分解模型进行对比,分析并评价数据分解方法对于模型预测性能的优化程度。
首先,将相邻两天的收盘价格进行比对,使用如下的对数收益率计算公式,得到收益率序列:
基于该收益率序列,如下定义涨跌趋势trend:
本文所取样本中的涨平跌趋势数据量大约各占三分之一。在此设定下,为验证算法对未来价格和收益率的涨、平、跌三种情况的预测表现,定义如下的趋势准确率accuracy:
3.1 数据处理
所用数据通过网易财经下载,分别为沪深300指数2007年1月15日到2020年4月28日和上证指数1990年12月21日到2020年4月28日的收盘价、最高价、最低价、前收盘价、成交量和收益率数据。上述六个指标的数据将作为不使用数据分解模型的LSTM神经网络的输入变量。对于使用SW-VMD数据分解的预测模型,设定本征模态函数个数为6,收盘价以及收益率原始数据需分别按照图1的步骤进行变分模态分解,将得到的6个本征模态函数作为数据分解模型的输入变量。
首先,对数据进行ADF平稳性检验。当ADF检验结果小于1%、5%、10%水平下的拒绝原假设的统计值,则说明该序列是平稳的,否则是非平稳的。上证指数及沪深300收盘价及收益率序列平稳性检验结果如表1所示。从检验结果可知,两个股指的收盘价序列均为非平稳序列,收益率序列则为平稳序列。
为判定LSTM神经网络的模型性能,在使用神经网络计算之前,首先使用Hurst指数来验证所取收盘价和收益率时间序列数据的记忆性。上证指数和沪深300指数的收盘价和收益率时间序列的Hurst检验结果见表2。由表2可以看出,两种指数的收益率数据序列的Hurst值均属于区间[[0.45, 0.5]],根据Hurst指数的数值意义,说明选取的收益率时间序列均具有长记忆性,但具有弱反持续性,即在一定时间内上升后,下一时间段内下降。表2中收盘价的Hurst值均在0.5以上,这说明了收盘价序列也具有长记忆性且具有持续行为,也即在收盘价上升的情况会继续上升,下降的时候会持续下降。因为收益率值在零轴附近波动剧烈,涨跌变化较快,而收盘价序列则通常会出现持续上涨或持续下跌的趋势,这与Hurst指数的数值意义是一致的。
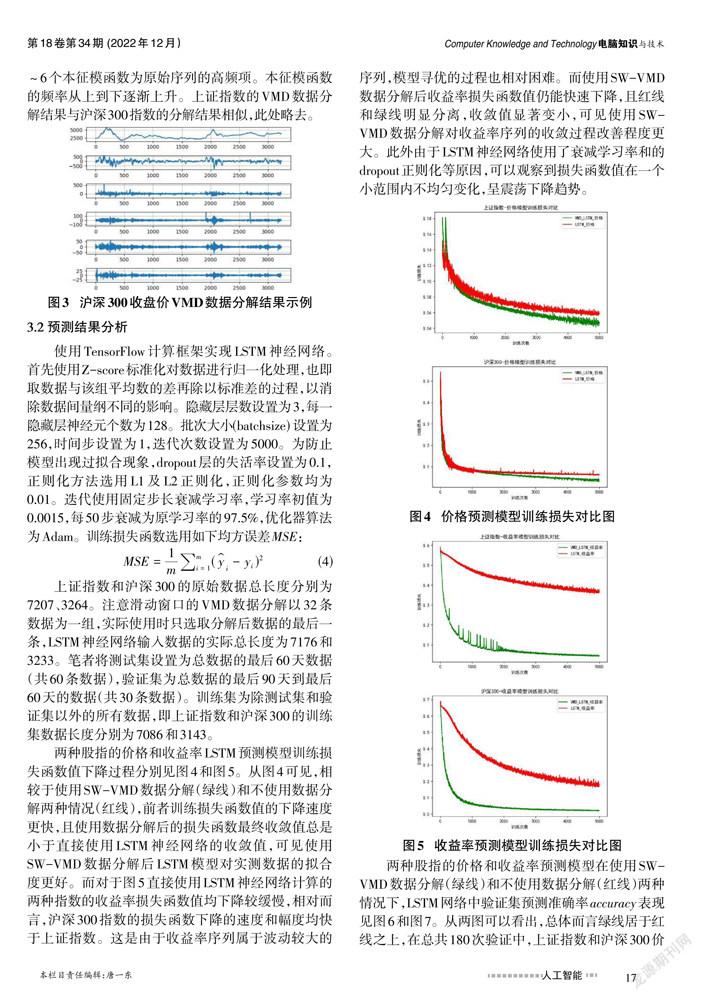
接下来,运用SW-VMD变分模态分解算法对两个股指的收盘价序列以及收益率序列进行分解,得到6个本征模函数IMF,以沪深300收盘价的VMD数据分解结果为示例,详见图3。图3中第一个本征模函数为原始序列的低频项,反映了原始序列的趋势情况,第2~6个本征模函数为原始序列的高频项。本征模函数的频率从上到下逐渐上升。上证指数的VMD数据分解结果与沪深300指数的分解结果相似,此处略去。
3.2 预测结果分析
使用TensorFlow计算框架实现LSTM神经网络。首先使用Z-score标准化对数据进行归一化处理,也即取数据与该组平均数的差再除以标准差的过程,以消除数据间量纲不同的影响。隐藏层层数设置为3,每一隐藏层神经元个数为128。批次大小(batchsize) 设置为256,时间步设置为1,迭代次数设置为5000。为防止模型出现过拟合现象,dropout层的失活率设置为0.1,正则化方法选用L1及L2正则化,正则化参数均为0.01。迭代使用固定步长衰减学习率,学习率初值为0.0015,每50步衰减为原学习率的97.5%,优化器算法为Adam。训练损失函数选用如下均方误差MSE:
上证指数和沪深300的原始数据总长度分别为7207、3264。注意滑动窗口的VMD数据分解以32条数据为一组,实际使用时只选取分解后数据的最后一条,LSTM神经网络输入数据的实际总长度为7176和3233。笔者将测试集设置为总数据的最后60天数据(共60条数据),验证集为总数据的最后90天到最后60天的数据(共30条数据)。训练集为除测试集和验证集以外的所有数据,即上证指数和沪深300的训练集数据长度分别为7086和3143。
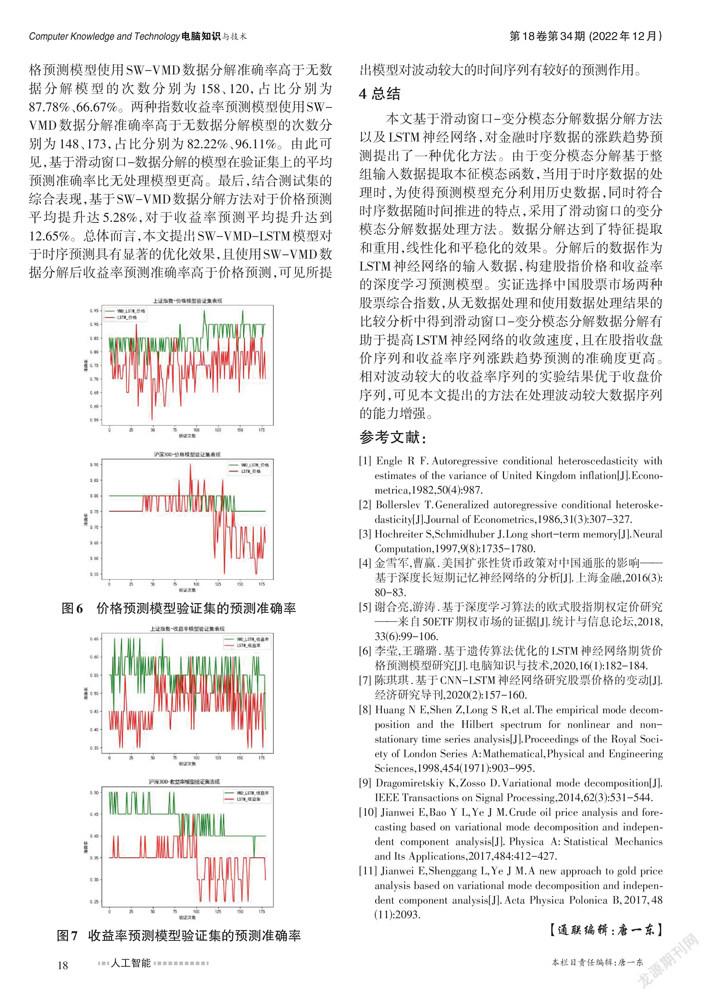
两种股指的价格和收益率LSTM预测模型训练损失函数值下降过程分别见图4和图5。从图4可见,相较于使用SW-VMD数据分解(绿线)和不使用数据分解两种情况(红线),前者训练损失函数值的下降速度更快,且使用数据分解后的损失函数最终收敛值总是小于直接使用LSTM神经网络的收敛值,可见使用SW-VMD数据分解后LSTM模型对实测数据的拟合度更好。而对于图5直接使用LSTM神经网络计算的两种指数的收益率损失函数值均下降较缓慢,相对而言,沪深300指数的损失函数下降的速度和幅度均快于上证指数。这是由于收益率序列属于波动较大的序列,模型寻优的过程也相对困难。而使用SW-VMD数据分解后收益率损失函数值仍能快速下降,且红线和绿线明显分离,收敛值显著变小,可见使用SW-VMD数据分解对收益率序列的收敛过程改善程度更大。此外由于LSTM神经网络使用了衰减学习率和的dropout正则化等原因,可以观察到损失函数值在一个小范围内不均匀变化,呈震荡下降趋势。
两种股指的价格和收益率预测模型在使用SW-VMD数据分解(绿线)和不使用数据分解(红线)两种情况下,LSTM网络中验证集预测准确率accuracy表现见图6和图7。从两图可以看出,总体而言绿线居于红线之上,在总共180次验证中,上证指数和沪深300价格预测模型使用SW-VMD数据分解准确率高于无数据分解模型的次数分别为158、120,占比分别为87.78%、66.67%。两种指数收益率预测模型使用SW-VMD数据分解准确率高于无数据分解模型的次数分别为148、173,占比分别为82.22%、96.11%。由此可见,基于滑动窗口-数据分解的模型在验证集上的平均预测准确率比无处理模型更高。最后,结合测试集的综合表现,基于SW-VMD数据分解方法对于价格预测平均提升达5.28%,对于收益率预测平均提升达到12.65%。总体而言,本文提出SW-VMD-LSTM模型對于时序预测具有显著的优化效果,且使用SW-VMD数据分解后收益率预测准确率高于价格预测,可见所提出模型对波动较大的时间序列有较好的预测作用。
4 总结
本文基于滑动窗口-变分模态分解数据分解方法以及LSTM神经网络,对金融时序数据的涨跌趋势预测提出了一种优化方法。由于变分模态分解基于整组输入数据提取本征模态函数,当用于时序数据的处理时,为使得预测模型充分利用历史数据,同时符合时序数据随时间推进的特点,采用了滑动窗口的变分模态分解数据处理方法。数据分解达到了特征提取和重用,线性化和平稳化的效果。分解后的数据作为LSTM神经网络的输入数据,构建股指价格和收益率的深度学习预测模型。实证选择中国股票市场两种股票综合指数,从无数据处理和使用数据处理结果的比较分析中得到滑动窗口-变分模态分解数据分解有助于提高LSTM神经网络的收敛速度,且在股指收盘价序列和收益率序列涨跌趋势预测的准确度更高。相对波动较大的收益率序列的实验结果优于收盘价序列,可见本文提出的方法在处理波动较大数据序列的能力增强。
参考文献:
[1] Engle R F.Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J].Econometrica,1982,50(4):987.
[2] Bollerslev T.Generalized autoregressive conditional heteroskedasticity[J].Journal of Econometrics,1986,31(3):307-327.
[3] Hochreiter S,Schmidhuber J.Long short-term memory[J].Neural Computation,1997,9(8):1735-1780.
[4] 金雪军,曹赢.美国扩张性货币政策对中国通胀的影响——基于深度长短期记忆神经网络的分析[J].上海金融,2016(3):80-83.
[5] 谢合亮,游涛.基于深度学习算法的欧式股指期权定价研究——来自50ETF期权市场的证据[J].统计与信息论坛,2018,33(6):99-106.
[6] 李莹,王璐璐.基于遗传算法优化的LSTM神经网络期货价格预测模型研究[J].电脑知识与技术,2020,16(1):182-184.
[7] 陈琪琪.基于CNN-LSTM神经网络研究股票价格的变动[J].经济研究导刊,2020(2):157-160.
[8] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A:Mathematical,Physical and Engineering Sciences,1998,454(1971):903-995.
[9] Dragomiretskiy K,Zosso D.Variational mode decomposition[J].IEEE Transactions on Signal Processing,2014,62(3):531-544.
[10] Jianwei E,Bao Y L,Ye J M.Crude oil price analysis and forecasting based on variational mode decomposition and independent component analysis[J].Physica A:Statistical Mechanics and Its Applications,2017,484:412-427.
[11] Jianwei E,Shenggang L,Ye J M.A new approach to gold price analysis based on variational mode decomposition and independent component analysis[J].Acta Physica Polonica B,2017,48(11):2093.
【通联编辑:唐一东】
