基于MPC的自动驾驶汽车横向控制算法研究
2022-02-20王开峰
王开峰
(重庆交通大学,重庆 400074)
0 引言
据公安部统计,截至2022年9月底,我国民用汽车保有量已达3.15亿辆。随着汽车行业的飞速发展,人民生活水平日益提高的同时,也带来了诸多的问题。据统计,我国每年发生的交通事故多达20多万起,其中绝大多数都是由于驾驶员操作不当引起的。自动驾驶技术作为缓解交通拥堵、降低交通事故发生率的有效解决方案,在过去10年中取得了巨大的进步。
自动驾驶技术的基本模块有感知、规划和控制模块。感知模块主要通过安装在车辆上的摄像头、雷达等传感器,感知周围环境的信息,如车道标记、障碍物位置、行人和道路交通情况等;规划模块收到感知端传来的周围环境信息后,综合车辆当前状态,规划出一条最优的行驶轨迹,发送给控制模块;控制模块主要负责向车辆生成具体的控制命令,以遵循规划端制定出的目标轨迹。
本文主要研究自动驾驶技术中的横向控制部分,横向控制主要负责控制车辆转向机构,使车辆按照目标轨迹完成转向动作。国内外对于这一过程的控制方法做了很多研究,邱泉等[1]针对自动驾驶汽车在受到外界扰动时容易出现的稳定性问题,设计了基于模糊滑模方法的横向控制器,以横摆角速度为控制量,可以有效地提高被控系统稳定性。彭炳顺等[2]为了解决轨迹跟踪这一问题,以二自由度动力学模型为对象,并带有前馈控制,设计了基于LQR算法地横向控制器,通过仿真验证了所设计的控制器对外部环境干扰和车辆内部的因素干扰有着良好的适应性,确保车辆能够快速且稳定地跟踪轨迹。梁栋[3]设计了一种基于模型预测控制算法的路径跟踪控制器,通过实验验证了其优良的控制性能。郝悦[4]对比分析了模糊控制算法、模型预测控制、自适应滑模控制和H∞控制技术对车辆车道保持控制的效果。
模型预测控制(MPC)是一种最优控制算法,已被证明是控制自动驾驶汽车的强大工具[5-6],主要得益于MPC可以处理输入、状态约束以及车辆动力学引入的非线性特性。此外,MPC能够处理约束,例如碰撞或轨迹约束,并可显式定义成本函数,为权衡控制目标提供了一种直观的方法。因此,本文将基于MPC设计自动驾驶车辆的横向控制器,首先建立了车辆系统的运动学和动力学模型,然后基于MPC设计了自动驾驶车辆的轨迹跟踪横向控制器,最后在Simulink/Carsim/Prescan联合仿真平台上对所设计的控制器进行仿真实验,验证了控制器具有良好的性能。
1 车辆系统建模
1.1 运动学模型
除了一些无模型的经典控制方法以外,许多现代控制理论大都依赖于被控系统精确的数学模型来完成控制器的设计,而对于自动驾驶车辆横向控制系统的设计来说,建立车辆的运动学与动力学模型往往也是第一步工作。
通常,在考虑车辆运动学模型的时候,会将复杂的车辆模型简化成单车模型,在单车模型中,将车辆的左右前轮合并等效为单个轮子,其中心点为A点,同样的后轮等效后的中心点为B点,并假设车辆仅处于低速状态,不考虑轮胎的侧偏特性,假设车辆不会发生侧向滑动。
根据几何关系可以得到该系统的运动学方程为:
(1)
式中,ψ为车辆的航向角,δf为前轮转角,l为车辆轴距,vr代表前后轴中心速度。
由于运动学模型仅建立在车辆与道路的几何关系基础上,不考虑车辆在实际行驶过程中受力的影响,因此其仅适用于低速无人车中,在中高速的工况中,并不适用。
1.2 动力学模型
当汽车在一些中高速工况下行驶时,车辆与道路间的相互作用力会使轮胎产生较大的形变,运动学模型已经无法满足车辆高精度控制的要求,需要进一步考虑轮胎的侧偏特性,建立车辆的动力学模型。在图1的单车模型中,假设轮胎具有线性侧偏特性,并将前、后轴两轮等效后的单个车轮的侧偏刚度设为C,可以得到车辆的二自由度动力学模型为:
(2)
式中,m为汽车整备质量,vx为车辆纵向速度,Iz为车辆绕z轴的转动惯量,a和b分别为车辆前后轴中心点到车辆质心的距离,β为车辆质心侧偏角,ψ为车辆横摆角,δ为前轮转角。
2 自动驾驶汽车轨迹跟踪横向控制器设计
2.1 模型预测控制原理
模型预测控制主要由3个部分组成,分别是预测模型、滚动优化以及反馈校正。预测模型是模型预测控制的基础,基于被控系统的模型,通过系统的当前状态和未来的控制输入变量,来预测未来被控系统的状态;模型预测控制中的滚动优化采用滚动式的有限时域优化策略,在每一时刻,控制器会求解该时刻起有限时段内的最优控制律,得到一系列的最优控制序列,并将最优序列的第一个值作为当前时刻的控制量作用于系统,系统执行后,在下一个采样时刻点,往后有限时域内根据更新后的状态重新计算最优控制序列,同样将控制序列的第一个控制量作用于系统,如此循环往复,控制系统始终实时的在被控系统最新状态下建立新的优化目标,进而得到每个时刻的最优控制量。
2.2 模型预测控制器的设计
自动驾驶汽车在轨迹跟踪过程中,需要不断消除跟踪误差,以达到良好的跟踪效果,跟踪误差又分为横向误差ed和航向误差ea,结合前文建立的车辆系统动力学模型式(2),可建立关于跟踪误差的线性微分方程组。控制器的控制目标是,以较小的控制代价使得跟踪误差尽可能地小,因此,可以将目标函数设置为如下形式:
J=eTQe+uTRu
(3)
其中,Q、R为权重矩阵,u为控制量,e为跟踪误差,目标函数中线性叠加部分第一项体现了控制器跟踪目标轨迹的能力,第二项体现了对于实现控制目标所需要的控制代价的限制。
为了将所建立的目标函数应用于车辆横向控制器中,还需要对其添加相关约束,以满足实际的控制要求,本文主要考虑车辆的前轮转角的硬约束需满足:
-30°<δ<30°
(4)
综合上述目标函数和约束条件,可得到MPC控制器在每个采样点需求解以下优化问题:
MIN{J=eTQe+uTRu}
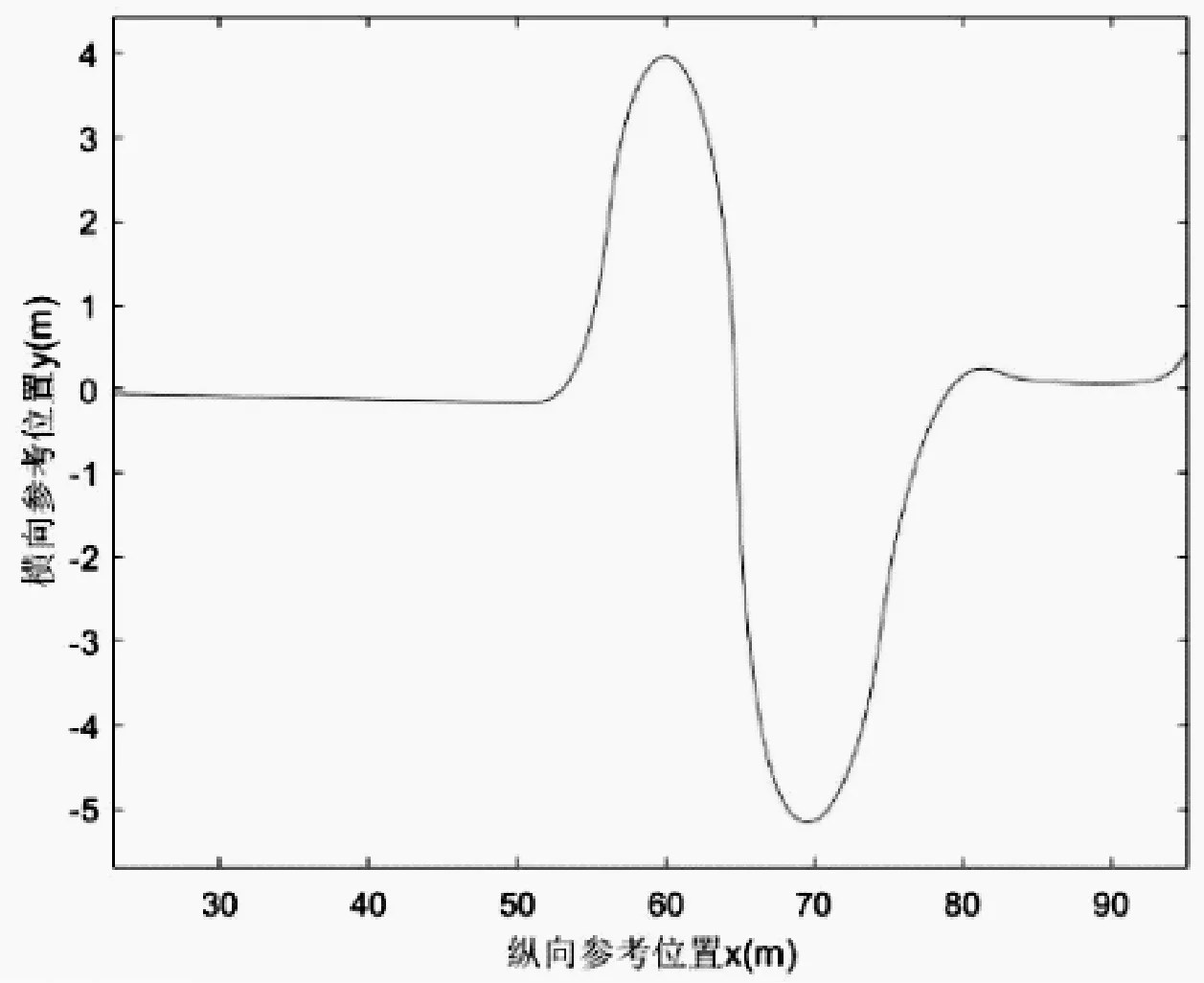
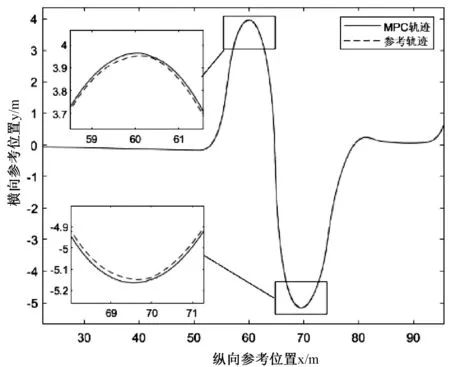
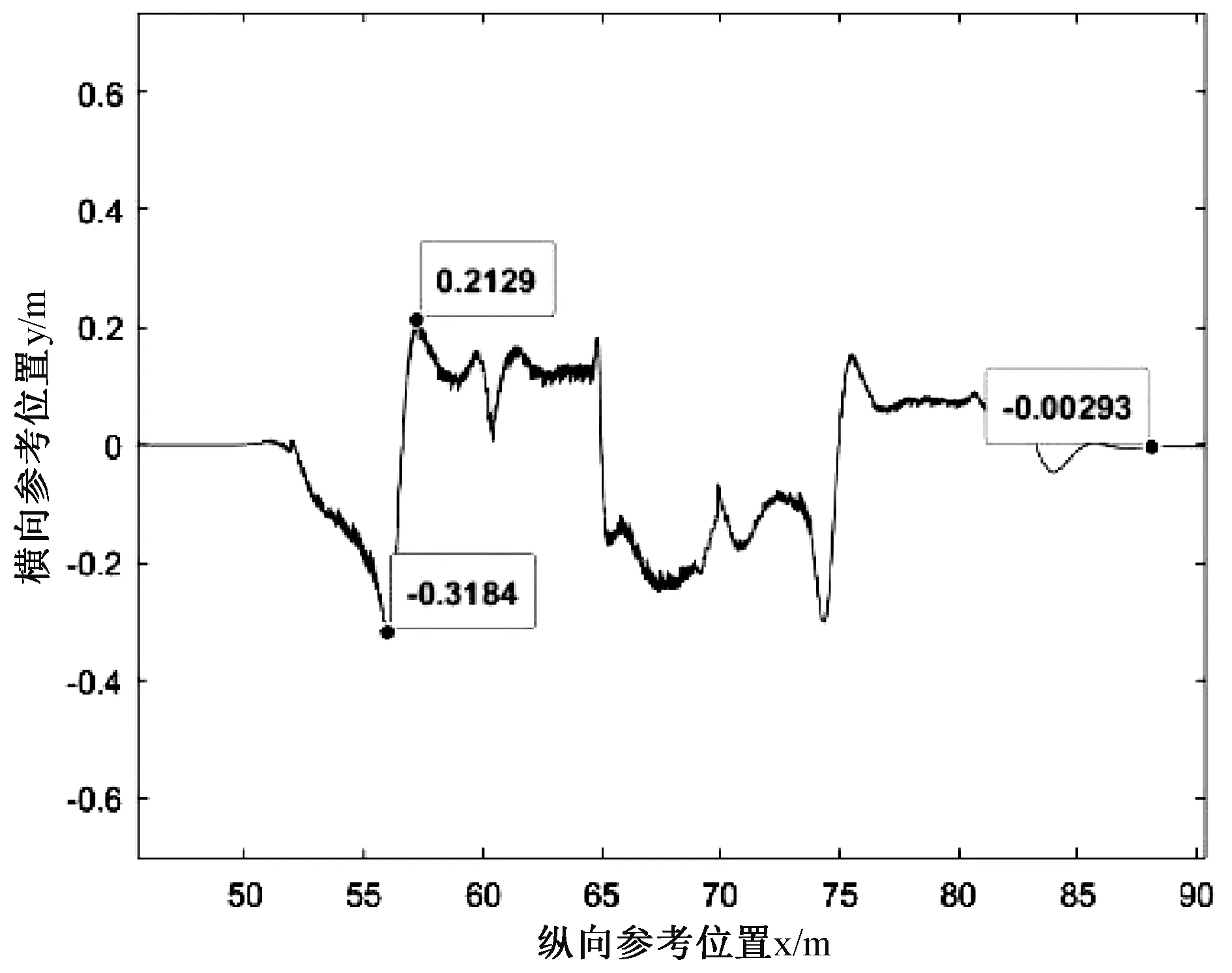
-30 (5) 求解得到每个采样点往后一段预测时域内的最优控制量序列,然后将控制序列的第一个元素作为控制器的输出作用于车辆系统,在每个采样点均重复以上优化求解过程,直到完成整个控制过程,实现车辆对轨迹的实时跟踪。 本文在搭建的Simulink/Carsim/Prescan联合仿真平台上,对设计的轨迹跟踪控制器进行仿真实验,以验证该控制器在自动驾驶车辆控制过程中的有效性。 首先在Carsim中选取了Audi A8为本次实验测试车辆,并将其动力学模型发送到Simulink中作为被控系统,然后通过Prescan部署了一个在汽车行驶稳定性测试中经典的双移线工况,该工况设定的轨迹如图1所示。 图1 参考跟踪轨迹 基于上文的理论推导,在MATLAB中完成对模型预测控制算法的编写,并与Carsim中获取的车辆动力学模型以及Prescan中搭建好的实验场景进行联合仿真实验,设定车辆纵向速度恒定为15 m/s,路面附着系数为0.85。实验结果如下,图2为参考轨迹与实际行驶轨迹对比,图3为横向跟踪误差变化曲线。 图2 跟踪轨迹对比 仿真车辆实际行驶轨迹与参考轨迹相差很小,只有在弯道处会出现较小的偏差,如图2所示。车辆在整个路径跟踪过程中最大的横向误差为0.318 m,出现在入弯阶段,在车辆驶出弯道后跟踪误差可以在较短时间内收敛到0.003 m,且无明显震荡,具有一定的稳定性,可以满足自动驾驶车辆实际控制需求,如图3所示。 图3 横向跟踪误差变化曲线 本文主要针对自动驾驶汽车的横向控制过程设计了基于MPC的轨迹跟踪控制器。首先,介绍了模型预测控制算法的基本原理;其次,从跟踪误差模型、目标函数、约束条件3个方面来设计模型预测控制器;最后基于Simulink/Carsim/Prescan搭建的联合仿真实验平台,对所设计的横向控制器进行实验验证了其有效性。3 联合仿真实验分析
3 结语
