单轴压缩下EPS泡沫的力学性能试验研究

邵成健，徐永福，杨同帅，付 苗

（上海交通大学船舶海洋与建筑工程学院，上海 200240）

0 引言

聚苯乙烯泡沫（Expanded Polystyrene，EPS）是一种轻型高分子聚合物，它是采用聚苯乙烯树脂加入发泡剂，同时加热进行软化并产生气体而形成的一种硬质闭孔结构的泡沫塑料。因其具有质轻、力学性能好、自立性和耐久性强、施工方便、环境友好等优点，对解决路堤失稳、桥头跳车、路基冻害和新老路基拼接等问题有良好的处理效果，目前广泛运用于建筑和包装行业中［1-4］。

关于EPS 泡沫的力学性能，目前国内外众多学者对其进行了详细的试验研究，并得到了许多有用的成果［5］。熊志远等［6］研究了密度和应变率对EPS 泡沫准静态压缩力学行为的影响，并指出EPS 的密度与其屈服强度呈线性关系，同一密度的EPS 在不同加载速率下其线弹性模量基本不变而屈服强度随加载速率增大而增加。Vaitkus等［7］通过对不同尺寸的EPS 泡沫板进行单轴压缩试验，提出了EPS 泡沫出现应力松弛时其衰减因数表达式。王志亮等［8］对EPS 泡沫冲击压缩和吸能特性进行了试验研究，认为泡沫初始密度和加载应变率对EPS 泡沫的吸能和冲压特性具有较大影响。Chen 等［9］研究了两种不同密度的EPS 泡沫在准静态和动态荷载作用下其力学特性，指出EPS 泡沫的静力强度和弹性模量随密度增加而增大，抗拉强度和屈服应变在动荷载作用下均随应变率增加而增大。毛快等［10］在室温环境下对三种不同密度的EPS泡沫进行单轴压缩蠕变试验，认为同密度的EPS 其蠕变量值随着应力水平的增大而增大，同应力水平下的EPS其蠕变量随着密度的增大而减小，并在试验的基础上提出了包含密度影响的EPS 压缩蠕变模型。尽管在EPS泡沫的强度和变形特性方面［11-13］，国内外学者都做了较多的研究，大多是从不同密度考虑，但是关于尺寸效应和加载速率对EPS 力学性能的影响的研究较少［14-15］。

鉴于上述问题，本文通过对不同尺寸的EPS 泡沫试样进行单轴压缩试验，研究其不同加载速率情况下试样的应力-应变曲线，屈服强度和初始弹性模量与尺寸、加载速率的关系，为更全面掌握EPS 泡沫的力学性能提供理论依据。

1 试验测试

1.1 试验材料

本文试验测试的材料为南京鳄鱼节能科技有限公司生产的普通聚丙乙烯泡沫，试样密度为15.22 kg／m3，边长D分别为200、100、50 mm 的立方体，如图1所示。

图1 不同尺寸试验材料

1.2 试验设备

图2 所示为EPS 的单轴压缩试验测试用MTS＼SANS电液伺服万能试验机，荷载最大量程为300 kN，可以自动采集轴向荷载和位移值，测量精度为±1%。EPS试件的应力-应变曲线由下式计算得到：

图2 液压伺服试验机

式中：σ为应力，kPa；F为作用在试块上的力，kN；A为试样接触面积，m2；ε为应变，%；Δl和l分别为试样的压缩变形量和垂直高度，mm。

1.3 试验方法

在常温下，对不同尺寸的EPS 泡沫立方体的试样，分别以10、20、40 mm／min 的加载速率进行单轴压缩试验，每个尺寸的试样在同一加载速率下需进行3次试验。

如图3 所示为本文测试试验中EPS 泡沫屈服强度及弹性模量取值图，初始弹性模量取应力-应变曲线中线弹性阶段的斜率；将EPS泡沫产生10%应变时所对应的应力作为屈服强度，这与国内外学者关于EPS泡沫强度的定义方法是一致的［5］。

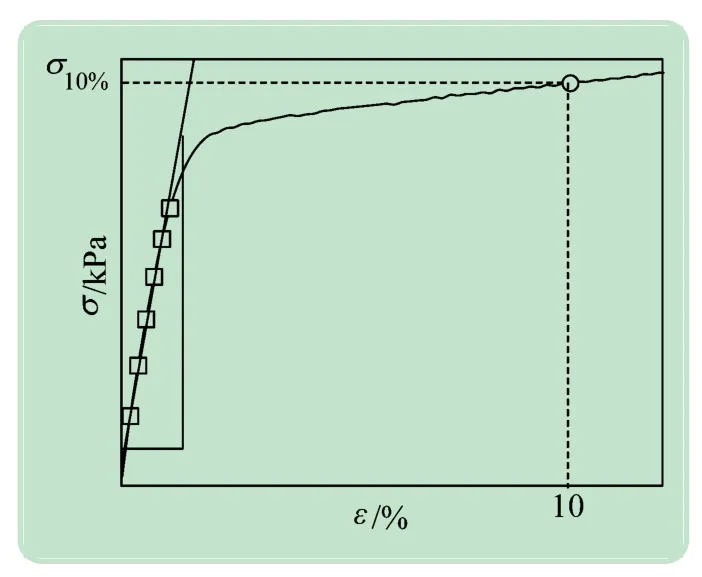
图3 EPS泡沫屈服强度及弹性模量取值

2 结果与讨论

2.1 应力-应变曲线

图4 所示为EPS 泡沫试样在无侧限单轴压缩情况下其应力-应变曲线，由图可知，试样在受压变形过程中经历3 个阶段：

图4 EPS泡沫试样应力-应变曲线

（1）OA段，线弹性阶段。加载初期，EPS 泡沫的应力与应变呈线性关系，这主要是由于材料本身内部结构造成的，材料内部封闭气体产生微小变形，而其本身内部封闭气体的空腔结构并未发生破坏。

（2）AB段，塑性屈服平台阶段。随着荷载的增加，应力达到弹性极限并继续增加，试样开始出现屈服破坏，EPS泡沫颗粒的空腔结构开始逐渐破裂。这一阶段，应变增加较快而应力增加较小。

（3）BC段，硬化阶段。随着EPS 泡沫颗粒不断破裂，试样中气体含量逐渐减小，继续加载，开始出现应力急剧增大而应变增加逐渐缓慢的现象。

图5 所示为不同加载速率下边长为100 mm 的EPS泡沫的应力-应变曲线，从图中可以明显看出，加载速率对EPS泡沫材料的应力大小有明显影响，加载速率越大，相同应变对应的应力值也就越大。但是其应力-应变曲线变化规律都是一致的，都经历了线弹性、塑性屈服平台和硬化3 个阶段。

图5 不同加载速率下EPS泡沫的应力-应变曲线

图6 所示为在加载速率为20 mm／min 情况下，3种不同尺寸的EPS 泡沫在无侧限单轴压缩下得到的应力-应变曲线。由图可知，尺寸因素对EPS泡沫试样应力-应变曲线有较大影响，尺寸越大，相同应变所对应的应力值也就越大。但是对于不同尺寸的试样，其应力-应变曲线变化规律均一致。

图6 不同尺寸下EPS泡沫的应力-应变曲线

2.2 屈服强度

图7 所示为不同加载速率及不同边长立方体尺寸下EPS泡沫的屈服强度的变化规律。

图7 EPS泡沫的屈服强度

（1）不同加载速率。由图7（a）可知，同一尺寸的试样在无侧限单轴压缩情况下，加载速率越大，屈服强度越高。以边长为200 mm 的试块为例，当加载速率分别为10、20、40 mm／min时，其屈服强度的平均值分别为79.28、85.68、95.68 kPa，加载速率为20 mm／min的试样屈服强度σs比速率为10 mm／min的大8.1%，加载速率为40 mm／min 的试样平均屈服强度比速率为20 mm／min 的要大11.67%，说明加载速率对EPS泡沫屈服强度大小的影响明显。分析其原因，主要是由于加载速度越大，塑性变形也就越快，变形后的材料储能越高，应变硬化率越高，导致材料本体硬度提高，屈服强度增大。

（2）不同边长立方体样品。由图7（b）可知，尺寸对EPS泡沫试样的屈服强度有明显影响，尺寸越大，屈服强度越高。以加载速率为20 mm／min 为例，边长为50、100、200 mm 的试样其平均屈服强度分别为78.82、84.67、93.68 kPa，尺寸为100 mm 的试样平均屈服强度比尺寸为50 mm的试样大7.42%，而尺寸为200 mm的试样平均屈服强度比尺寸为100 mm 的试样高10.64%，说明EPS 泡沫试样的屈服强度随尺寸增大而增大。

2.3 弹性模量

EPS泡沫是一种特殊材料，在荷载单轴压缩下，其应力大小一直增加，试样经历了弹性、屈服和硬化阶段，当应力大小超过弹性极限后，随着荷载不断增加，其弹性模量大小先减小后一直不断增大。图8 所示为不同加载速率及不同边长立方体尺寸下EPS 泡沫的初始弹性模量的变化规律。

（1）不同加载速率。由图8（a）可知，对于同一尺寸的EPS 泡沫试样，加载速率对其弹性模量影响较小。以边长为200 mm的试样为例，在加载速率为10、20、40 mm／min时，EPS泡沫试样的平均弹性模量分别为3.45、3.55、3.88 MPa，加载速率为20 mm／min比10 mm／min的平均弹性模量大3.1%，40 mm／min 比20 mm／min的平均弹性模量大9.1%，说明加载速率对EPS泡沫的初始弹性模量影响并不明显。

图8 EPS泡沫的初始弹性模量

（2）不同边长立方体样品。由图8（b）可知，对于同一加载速率的情况下，尺寸越大，EPS泡沫的初始弹性模量也就越大。以加载速率为20 mm／min 为例，边长为50、100、200 mm 的立方体试样其平均初始弹性模量分别为1.97、3.2、3.56 MPa，边长为100 mm的试样平均初始弹性模量比边长为50 mm 的试样大63.28%，边长为200 mm的试样平均初始弹性模量比边长为100 mm的试样大10.6%，说明EPS 泡沫的初始弹性模量与试样尺寸密切相关。

3 结语

本文通过对不同尺寸的EPS 泡沫在不同的加载速率下进行单轴压缩试验并对试验数据进行分析，结果表明：EPS泡沫在单轴压缩情况下，其应力-应变曲线主要经历3 个阶段为线弹性、塑性屈服平台和硬化阶段；对于同一尺寸的试样，EPS泡沫的屈服强度随加载速率增大而增大，而弹性模量大小受加载速率影响较小，其值基本保持不变；在同一加载速率情况下，EPS泡沫的屈服强度和弹性模量均随试样尺寸的增加而显著增加。

未来进一步可从微观角度研究材料结构及其在荷载作用下的破坏机理，便于全面掌握EPS的性能。