基于多元表征理论的高中函数概念教学设计

杨兴 唐雪敏 钱淑渠

【摘 要】概念表征是教育心理学的一个关注点。研究者从多元表征理论的角度探讨概念教学，并以“函数概念”为例，构建函数概念的课堂教学模式，设计了以“建立表征，形成概念”和“转换表征，深化概念”为核心的函数概念教学过程，帮助学生构建函数的多元表征系统，建立完整的函数概念。

【关键词】多元表征理论;函数概念;教学设计

【作者简介】杨兴，贵州师范大学在读硕士研究生，主要研究方向为中学数学教育;唐雪敏，贵州师范大学在读硕士研究生，主要研究方向为中学数学教育;钱淑渠，安顺学院教授，硕士研究生导师，主要研究方向为计算智能、数学教育。

【基金项目】安顺学院研究生创新专项基金资助（asxyyjscx202106）;贵州省教育教学综合改革项目基金资助（黔教合KY字2021139）

从数学本身的发展来看，数学概念的来源一般有两个方面：一是直接从客观事物的数量关系和空间形式反映而得，二是在抽象的数学理论基础上经过多级抽象所获[1]。数学概念的建构要经历从外部表征到内部表征的深化。而从学生认知的角度看，数学概念的学习是人脑对数学多元表征信息进行加工与储存的过程，由于学生认知方式存在差异，对数学概念的表征方式不同，因此单一的表征方式已经不能满足学生认知发展的需求。然而，在实际教学中，很多教师往往忽视了学生认知方式的差异，很少关注到数学概念的多元表征。由于教师创设的问题情境单一，只注重函数解析式而忽视函数的其他表征形式，导致学生积累的函数背景不够丰富，概念的抽象过程生硬，不能在不同形式函数之间灵活转化。本文基于多元表征理论，重新审视函数概念的教学，根据函数多元表征的特点，构建函数概念的课堂教学模式，即教师从实际生活情景引入函数的解析式表征、图像表征以及表格表征，引导学生借助集合语言由函数外部表征转化到内部表征，从“变量说”过渡到“对应说”，从而建立完整的函数概念。

一、教学设计背景

（一）教科书和学情分析

课程标准规定高中阶段函数概念教学的核心在于帮助学生建立完整的函数概念，包括“变量说”和“对应说”。数学概念的定义离不开数学对象的表示。因此，人教版教科书设置了“函数的概念”和“函数的表示法”两个模块，按照“三个生活中的函数—用集合语言刻画函数—函数的定义域和值域—函数的三种表示方法”的路径来呈现，指出要通过函数的不同表示法让学生加深对函数概念的认识[2]。高一学生在初中依据变量之间的依赖关系学习了函数的概念，对函数的各种形式已有了初步的感知，但是缺乏对函数对应关系精确的刻画。因此，本节课的难点在于：一是如何借助集合语言精确刻画不同形式的函数，从而凸显函数的对应关系;二是如何建立函数表征之间的联系，从而能在实际应用中选择恰当的表征方式。

（二）课堂教学模式

数学学习与思维的过程和结果，既有内隐心理层面的反应，也有外显可视、可听、可感的数学化表达，表现为数学多元表征学习[3]。前者可以称为数学知识的心理表征，也叫内在表征，后者可以称为数学知识的外在表征。外在表征的丰富性照顾到学生的认知差异，内外表征的相互转化有助于学生对数学概念的理解。多元表征理论下的概念教学就是基于学生已有的知识经验呈现不同的概念表征形式，通过表征间的转換，从不同角度丰富概念的理解，建立新的概念表征系统。

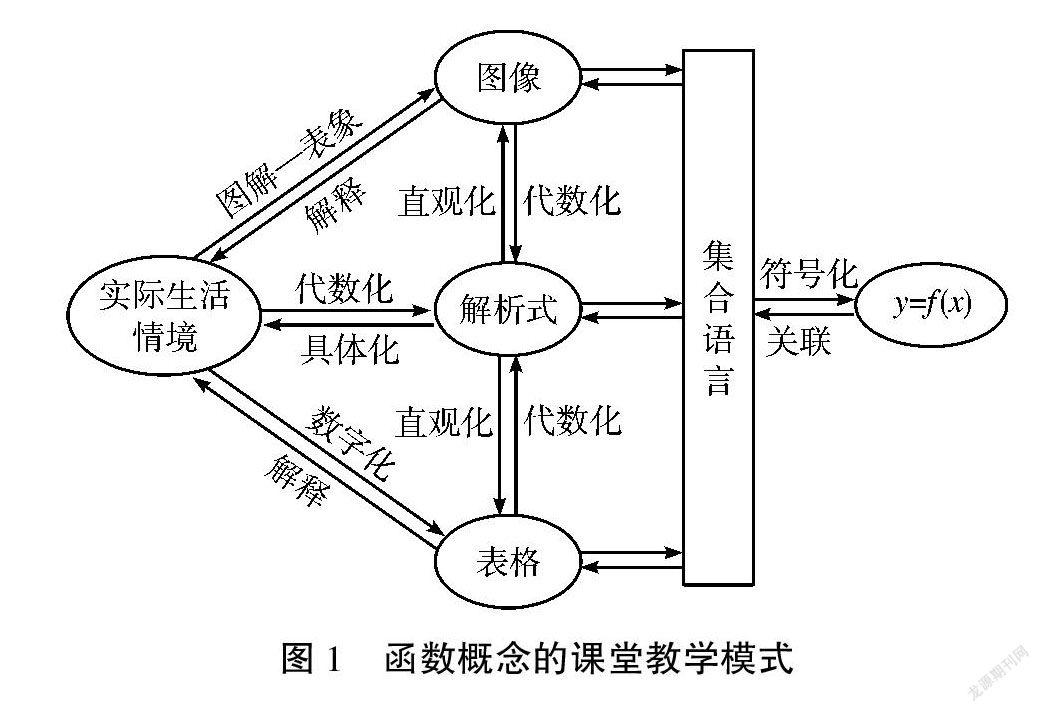
在中学阶段，函数本身就是一个丰富的表征系统，具体表现在：作为形式概念的函数符号（y=f（x））和操作程序的对象（输入—输出箱），既有代数的特征（函数解析式）和几何的特征（函数图像），又有数的特征（函数的列表表示）。根据数学教育心理学家莱什提出的数学概念的表征系统[4]，结合函数概念的特点，函数概念的课堂教学模式如图1所示。

该教学模式以实际生活情景为背景，通过三种不同的外部表征，使学生体会到函数的不同表示方式。遵循“由具体到一般，由一般到抽象”的函数概念发展过程，其核心在于以集合语言为载体，通过函数外部表征之间的转化，由函数的“变量说”过渡到“对应说”，使学生进一步理解函数的定义域和对应关系的意义，从而实现思维质的飞跃。值得注意的是，该教学模式虽然没有呈现语言表征与动作表征，但语言表征和动作表征是各种静态表征转化的“催化剂”，无论是外显的活动还是内隐的心智操作，都应该贯穿于整个学习过程中。笔者将函数概念的教学过程分为两个阶段：一是建立表征，形成概念;二是转换表征，深化概念。

二、教学过程设计

（一）建立表征，形成概念

1.语言表征和解析式表征——概念代数化

从函数概念的“变量说”出发创设问题情境，以学生熟悉的自然语言描述和解析式入手，引入集合语言，让学生初步了解如何用集合语言精确刻画函数。

问题1 某“复兴号”高速列车加速到350 km/h后保持匀速运行半小时。这段时间内，列车行进的路程用S（单位：km）表示，运行时间用t（单位：h）表示。

（1）S是t的函数吗？你是怎么想的？

（2）有人说：“按照对应关系M=350 t，这趟列车加速到350 km/h后，再运行1 h就前进了350 km。”你认为这个说法正确吗？

对于该题的第（1）问，学生会先表示出列车行进路程的表达式M=350t，结合初中一次函数的解析式y=kx+b，很容易判断出S是t的函数，不过此时学生的思维仅停留在解析式表征，接着教师引导学生回忆初中函数的定义，帮助学生初步建立语言表征与解析式表征之间的转化，但学生的思维还只是停留在外部表征层面，需要向内转化。对于第（2）问，教师要先引起学生的认知冲突，接着指出函数“变量说”定义的局限性，并示范给出S与t的对应关系的更精确化描述：t的变化范围是数集A1=t0≤t≤0.5，S的变化范围是数集B1=S0≤S≤175。对于数集A1中的任意时刻t，按照对应关系S=350 t，在数集B1中都有唯一确定的路程S和它对应。

2.图像表征和表格表征——概念直观化

教师创设无法用解析式表示函数的问题情境，引发学生的认知冲突。在用集合语言描述图像函数和表格函数的过程中，学生体会到函数的本质特征——对应，建立了直观化的表征。

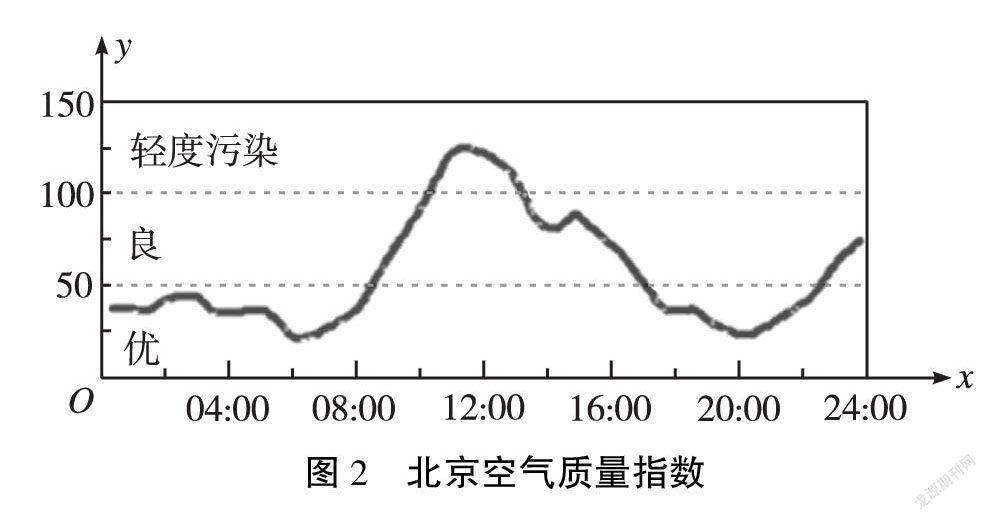
问题2 图2是北京市2016年11月23日的空气质量指数（Air Quality Index，简称AQI）变化图。

（1）如何根据该图确定这一天任意时刻t h的空气质量指数（AQI）的值I？你认为这里的I是t的函数吗？

（2）你能仿照问题1给出这个函数精确化的描述吗？

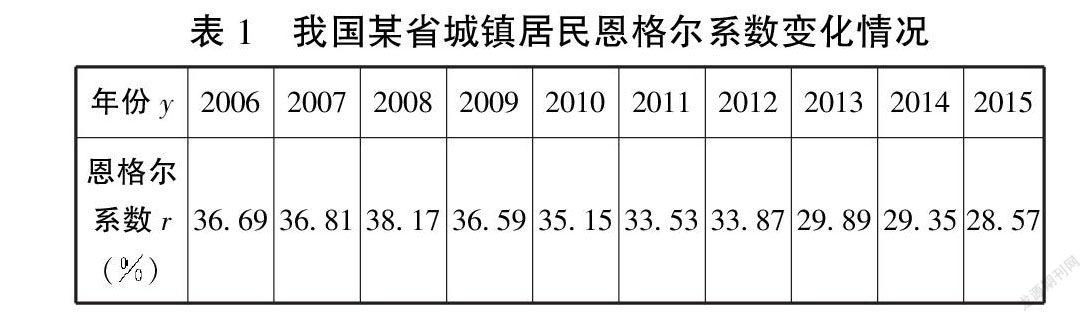
问题3 国际上常用恩格尔系数r（r=食物支出金额总支出金额）反映一个地区人民生活质量的高低，恩格尔系数越低，生活质量越高。表1是我国某省城镇居民恩格尔系数变化情况，从中可以看出，该省城镇居民的生活质量越来越高。你认为按表1给出的对应关系，恩格尔系数r是年份y的函数吗？你能用集合语言描述吗？

问题2和问题3分别以图像表征和表格表征来呈现函数，没有函数解析式作为函数概念的识别特征。这不仅要求学生理解“变量说”函数的定义，而且要求学生尝试用集合语言来给函数下定义。教师可以适时启发学生“按照图2中曲线所给的对应关系”“按照表1给出的对应关系”来描述函数。在这一教学环节，学生知道函数不仅能用解析式、图像和表格表示，还能用集合语言定义特殊函数。

3.集合语言表征——概念符号化

为引导学生用集合语言定义一般的函数，抽象概括出函数概念，教师可提出以下问题。

（1）问题1～3的3个函数有哪些共同点？有哪些不同点？

（2）你能用集合语言描述函数的概念了吗？

对于第（1）问，学生能比较容易地使用“变量说”函数的定义区分3个函数相同点与不同点，如都是一个x对应一个y，函数形式不同等，但不容易注意到定义域和值域。此时可以回顾并展示上述问题1～3函数的集合语言描述，使学生注意到上述函数的描述都包含两个非空数集A，B，都有一个对应关系，都是按照对于数集A中的任意一个数x，按照某种对应关系，在数集B中都有唯一确定的数y和它对应，接着教师进一步引导学生认识到，生活中还有很多诸如问题3那样无法写出解析式的函数，为了表示方便，我们引进符号统一表示对应关系，由此得到函数概念。

至此，学生借助集合语言，从函数的解析式表征、图像表征和表格表征过渡到符号表征，实现了函数的外部表征到内部表征的转换，但此时学生的表征系统还只是单向的，对概念的理解还不够深刻。

（二）转换表征，深化概念

经过上述教学环节，学生初步建构起函数概念，但还需要在多元表征之间互相转换，深化对概念的理解。从函数概念的课堂教学运行模式来看，教师应引导学生根据函数的概念理解函数解析式、图像和表格，并将三者关联起来，与生活情境建立联系。

1.根据函数概念理解函数解析式

要深入理解函数三要素，教师应引导学生理解以下内容：（1）发展函数概念的必要性;（2）定义域和值域都是非空数集;（3）理解函数的“一对一”和“多对一”;（4）定义域和对应关系决定函数的本质。以下通过一些例题帮助学生深化函数的概念。

例1 y=1与y=x-3+1-x的定义域和值域分别是多少？它们是函数吗？

教师引导学生认识到“变量说”函数的定义方式不仅不精确而且无法解释一些数学事实，使学生了解引入函数概念的必要性，理解函数的定义域和值域都是非空数集。

例2 判断下列对应是否为函数：

（1）x→y，这里y2=x，x∈N，y∈R;（2）当x为有理数时，x→1;当x为无理数时，x→0。

通过反例（1）和正例（2），学生加深了对函数“一对一”和“多对一”的认识。

例3 下列各组中的两个函数是否为同一个函数？

（1）f（x）=x2，g（x）=（x）2;（2）f（x）=x+1x，g（t）=t+1t。

以上例题让学生领悟到定义域和对应关系决定了函数的本质，同时也帮助学生掌握判断两个函数相等的方法。

2.根据函数概念创设生活情境

建立完整的函数概念，不仅能从生活情境中抽象出函数，还能根据函数的概念创设真实的生活情境，实现从数学的世界走向现实世界。

例4 试构造一个问题情境，使其中的变量可以用解析式y=x（10-x）来描述。

构造真实可信的问题情境需要分析该函数的定义域、值域、对应关系等，有利于综合函数各表征，培养学生逆向思维。

3.函数表征间的灵活转化

单一表征间的转化能巩固学生对函数的理解，而各表征间的灵活转化有助于学生全方位理解函数，建立函数的表征系统。

例5 给定函数f（x）=x+1，g（x）=（x+1）2，x∈R。

（1）在同一直角坐标系中画出函数f（x），g（x）的图像;（2）x∈R，用M（x）表示f（x），g（x）中的较大者，记为M（x）=maxf（x），g（x）。

该题将函数解析式、图像、抽象函数符号f（x）等函数表征综合在一起，不僅需要根据解析式画出函数图像，由函数图像想到对应关系，还要将函数符号f（x）看成可操作对象，根据对应关系构造新函数，帮助学生深化函数各表征间的转化，理解函数概念，掌握函数的不同表示方法。

三、结语

基于对学生表征差异和概念教学现状的认识，以多元表征理论为基础设计函数概念的教学过程，通过“建立表征，形成概念”“转换表征，深化概念”两个阶段，学生不仅理解了函数的本质，还知道了f（x）不仅是一个函数符号，还可以作为操作程序的对象，能展开表达式画出图像，建立比较完整的函数表征系统，对今后概念的运用，根据不同的需要选择恰当的函数表示起到一定帮助。但表征系统的流畅转化和数学概念意象的建立是一个不断深化的过程，本教学中“转化表征，深化概念”的设计只是抛砖引玉，表征间的转化、概念的深化还有拓展的空间。例如“根据图像求解析式”“根据表格求解析式”“根据图像构造生活情境”“根据表格构造生活情境”等表征间的转化问题应该在后续教学中有层次地呈现，循环往复，逐步深化。

因此，多元表征理论下的数学教学模式是以学习对象的多元表征特点为前提，以建立数学多元表征系统为目标，从学生已有的知识表征出发，教师呈现多元表征形式，引导学生建立表征、转化表征。这是一种以知识元出发来设计教学的观点，与当前提倡的单元教学理念相契合，这也给教师今后的数学概念、原理教学提供了一种新的思路。

参考文献：

[1]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[2]人民教育出版社课程教材研究所中学数学课程教材研究开发中心.普通高中教科书 数学 必修 第一册 A版[M].北京：人民教育出版社，2019.

[3]姚建法.数学多元表征研究综述[J].江苏教育研究，2020（13）：53-59.

[4]理查德·莱什，玛莎·兰多.数学概念和程序的获得[M].孙昌识，苗丹民，等译.济南：山东教育出版社，1991.

（责任编辑：陆顺演）