基于改进粒子群算法的固体火箭发动机总体设计优化方法

孙善春，谭泽荣，董元发

（1. 中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443002；2. 三峡大学机械与动力学院，湖北 宜昌 443002）

0 引言

固体火箭发动机推力大、推重比高、结构简单，在降低重力损失、提升质量比方面具有较大优势，已广泛应用于航天运载领域[1]。提升固体火箭发动机的整体性能对于航天技术和商业航天的发展具有重要意义。总体优化设计是提升固体火箭发动机性能的有效途径之一，国内外开展了大量研究工作。刘昕等[2]采用混合罚函数嵌套Powell法对远程机动导弹固体火箭发动机总体性能进行优化设计；杨军等[3]采用混合罚函数调用Powell法对战术火箭/固体火箭发动机一体化进行优化设计；李晓斌等[4]采用遗传算法对高压强固体火箭发动机性能/成本优化设计，为高工作压强下固体火箭发动机方案设计提供依据；杨青等[5]研究了一种改进的Pareto多目标遗传算法——IPGA算法来求解某运载火箭上面级固体推进剂火箭发动机多属性价值优化问题，提升了运载火箭的有效载荷并降低了成本。

固体火箭发动机设计涉及机械、材料、化学、热流体等学科领域，其设计参数与总体性能之间存在非常复杂的高维非线性关系，现有固体火箭发动机总体优化设计方法仍然存在收敛速度慢或容易陷入局部最优的问题。本文以质量比冲I0为优化目标建立固体火箭发动机总体优化设计数学模型，在经典粒子群优化算法的基础上引入动态惯性因子，提出一种基于改进粒子群算法的固体火箭发动机总体优化设计方法。

1 固体火箭发动机总体设计的数学模型

固体火箭发动机总体设计优化可以表征为有约束的非线性规划问题。将其数学描述为：对于所有设计参量X=（x1，x2，…，xn）T，求目标函数f（X）即I0的最大值，且满足约束条件：

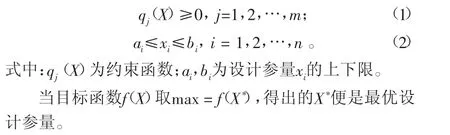
在固体火箭发动机总体设计中，一般把需要设计师设计且对发动机性能和设计质量指标影响较大的提出作为设计变量，以质量比冲I0最大为目标函数。本文选取以下变量为设计变量：发动机外径De、工作压强pc、扩张比εp、燃速r、工作时间ta、燃烧室长度L。

质量比冲I0与总冲、总体质量、比冲、燃烧剂的质量、

式中：mc为燃烧室壳体质量，与壳体壁厚、发动机外径、壳体材料密度密度、燃烧室长度有关；ms为燃烧室热防护层质量，与工作时间、发动机外径、壳体壁厚、热防护层材料密度、热防护层的烧蚀速率有关；mn为喷管结构质量，与喷管结构、喉截面积、扩张比、收缩比、工作压强、工作时间、材料特性有关；mign为点火药量质量;ma为其他结构质量，由燃烧室壳体质量与经验系数估计。

界限约束和不等式约束条件合并构成设计变量的可行域。

2 基于惯性因子动态化的改进粒子群算法

2.1 引入惯性因子ω

粒子群优化算法（particle swarm optimization,PSO）最早源自对鸟类捕食问题的研究，由Kennedy和Eberhart在1995年提出的。为平衡收敛的全局性和收敛速度，本文在经典PSO算法的基础上引入惯性因子ω，用于调整粒子的全局和局部搜索能力；惯性因子ω描述了粒子上一代速度对当前代速度的影响。图1所示为引入惯性因子ω后的PSO算法流程图。

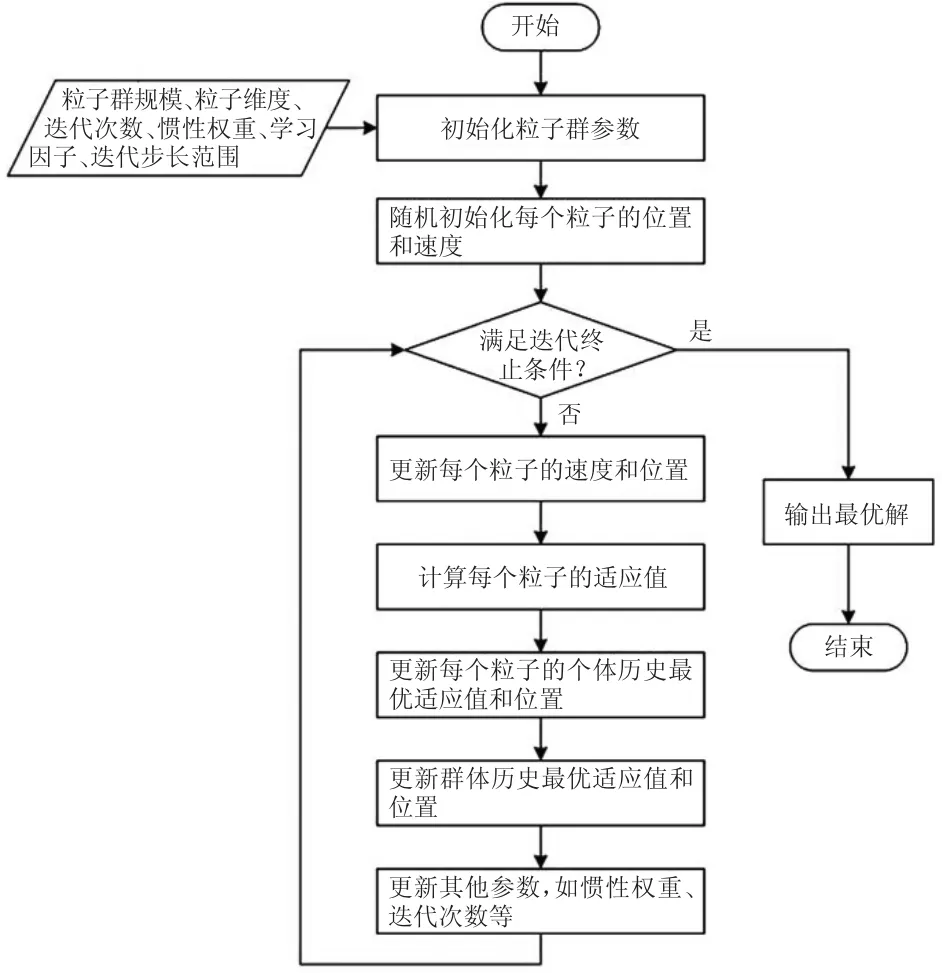
图1 引入惯性因子ω后的PSO优化算法流程图

算法迭代过程中，每个粒子下一步的移动方向受惯性方向、个体最优方向和群体最优方向共同影响，引入惯性因子ω后的粒子运动更新公式为:

2.2 惯性因子ω的自适应调整

惯性因子ω是描述粒子局部寻优能力和局部寻优能力，且惯性因子不能为负值。较大的ω值有利于跳出局部最优，而较小的ω有利于算法收敛。实际优化问题往往先通过全局搜索快速收敛于某一区域，然后通过局部精细搜索获得高质量解，因此动态ω能获得比固定值更好的寻优结果，本文采用线性递减权值策略：

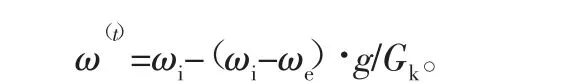
式中：Gk为最大迭代次数；g为当前迭代次数；ωi为初始惯性权值；ωe为迭代至最大进化代数时的惯性权值。一般典型权值为ωi=0.9，ωe=0.4。着迭代次数的增加逐步逼近最优值；惯性因子动态化算法在迭代150次左右完全收敛。最终优化结果如表1所示，与经验设计结果相比，采用改进粒子群算法优化设计结果质量比冲更大。

表1 粒子群算法优化结果

3 算例

图2 粒子群算法优化过程对比图

4 结论

采用基于惯性因子动态化的改进粒子群算法对固体火箭发动机进行总体设计优化，算例表明，该方法可有效提高固体火箭发动机的性能指标，为固体火箭发动机的总体优化设计提供了可行的解决方法。未来可考虑对发动机壳体及装药加工制造的不确定因素进行深入分析和建模，开展性能、成本、可靠性多目标优化设计，并在固体火箭发动机的优化设计的基础上进行鲁棒性优化设计，提高优化设计的可行性和实用性。