基于机器学习的SMAP卫星海表盐度反演

柳青青,张亚姝,徐 茗,李洪平*,刘海行

(1.中国海洋大学 信息科学与工程学院,山东 青岛 266100;2.青岛大学 商学院,山东 青岛 266100;3.自然资源部 第一海洋研究所,山东 青岛 266061)

海表盐度(Sea Surface Salinity,SSS)是实现全球水循环和海洋动力学的重要参量[1],决定海水的基本性质。海表盐度受到降水、蒸发量等气候因素影响,其变化直接影响海水密度,而海水密度的上下波动会反作用于全球气候变化和海洋循环,对全球气候的海-气-热交换调节起到至关重要的作用[2]。因此,对于海表盐度(SSS)反演精度的研究显得尤为重要。

目前国际上采用的研究海表盐度的实测数据包括浮标、船舶、系泊设备、漂流器等传输的测量数据;遥感数据包括欧洲空间局(European Space Agency,ESA)2009年发射的SMOS(Soil Moisture and Ocean Salinity)卫星,2011年美国国家航空航天局(National Aeronautics and Space Administration,NASA)与阿根廷航天局(Comision Nacional Argentina del Espacio,CONAE)联合发射的Aquarius/SAC-D卫星,以及NASA 2015年发射的SMAP(Soil Moisture Active and Passive)卫星等发布的盐度产品。Sabia等[3]研究发现,SMOS虽能有效反演SSS,但其产品精度较低;而Aquarius/SAC-D虽观测精度较高,但仅工作了3年零9个月,无法提供充足的科研数据,导致对分析SSS变化趋势的作用有限。Tang等[4]表明,2015年发射升空的SMAP卫星可以提供全球SSS数据,与具有100 km空间分辨率Aquarius/SAC-D相比,SMAP不仅提供了大约40 km以及平滑至约70 km的较高空间分辨率的SSS数据,而且填补了SMOS和Aquarius/SAC-D对部分海域SSS观测的空白。因此,本研究选用SMAP卫星海表盐度反演产品作为研究对象建立反演模型。

利用海表发射率可以反演海表盐度。SMOS卫星直接对大气顶观测亮温进行反演,而SMAP和Aquarius卫星却是首先将观测亮温还原至海表,然后对平静海面亮温进行反演。基于海水介电常数模型和海面亮温模型,国内外学者提出了L波段的垂直-水平双极化K-S模式反演算法。在传统反演模型的研究中,李志[5]利用L波段亮温资料反演黄海近岸SSS,平均绝对误差(Mean Absolute Error,MAE)达到0.288;赵红等[6]利用SMOS卫星L2辅助数据建立多元回归模型反演南海海域SSS,点对点精度为0.224 2;Blume和Kendall[7]改进K-S模式,将L波段与C波段组合的均方根误差(Root Mean Square Error,RMSE)达到0.25。

相对于具有局限性的传统反演模型,机器学习在海洋遥感方面有望得到具备更高精度的反演结果[8]。李长军等[9]采用浅层BP神经网络建立基于SMOS卫星的SSS反演模型,提高了南海海域SSS反演精度;艾波等[10]结合MODIS(Moderate Resolution Imaging Spectroradiometer)遥感影像和实测浮标数据,运用深度神经网络(Deep Neural Network,DNN)对海表温度进行反演,精度达到0.98℃;Liu等[11]利用深度神经网络和随机森林(Random Forest,RF)算法,选用潜在氢、叶绿素a浓度、海表温度和总无机氮作为输入参数对香港海域SSS进行反演,表明DNN具有良好的性能;Moussa等[12]认为浅层多层感知机(Multiple Layer Perceptron,MLP)比多重非线性回归(Multiple Nonlinear Regression,MNR)方法精度更高,从海表温度和纬度参数方面估计了SSS。张勇[13]将太平洋中部海域SMOS卫星L2数据反演的SSS1、SSS2和SSS3三种盐度产品与3种核函数下的支持向量机模型反演数据进行比较,相对于RMSE为0.6左右的SMOS卫星反演产品,支持向量机SVM(Support Vector Machine)在SSS反演中具有较高的精度,其RMSE误差在0.1～0.2。

本研究选取SMAP卫星V4.0 L2C产品中的5项辅助数据作为反演参数,以Argo(Array for Real-time Geostrophic Oceanography)浮标采集的实测盐度数据为实际输出,建立2种神经网络模型以拟合参数与SSS之间的非线性关系,将模型反演结果与SMAP卫星两种海表盐度产品(SSS_SMAP_70 km,SSS_SMAP_40 km)进行对比,以期提高遥感盐度精度,为相关研究提供更高质量的数据支撑。

1 数 据

1.1 Argo浮标数据

Argo计划于1998年提出,迄今为止,已在全球海洋中布放了5 000个以上浮标设备[14],是当今全球海洋实测数据(如海表温度、海表盐度等)的最主要来源之一。

研究数据源自Argo数据管理中心,选取2019年5月至2020年5月北太平洋部分海域(135°～165°E,15°～45°N)共10 386个站位点的有效Argo浮标数据。参考Boutin等[15]提出的Argo浮标数据水深质量控制原则,将数据集中于水深0.5～10 m的Argo盐度数据作为海表盐度数据。

1.2 SMAP卫星数据

SMAP卫星运行在太阳同步晨昏轨道,轨道高度685 km,重访周期为3 d。该卫星于2015年1月31日发射,搭载双极化L波段被动微波辐射计传感器以及频率在1.22～1.30 GHz调整的主动合成孔径雷达。其辐射计可以探测全部4个斯托克斯参数,分辨率为40 km。本研究采用SMAP卫星搭载的L波段辐射计观测数据产品L2C进行后续分析。SMAP卫星盐度产品资料具有多种形式,部分产品的详细描述见表1。

表1 SMAP卫星产品描述Table 1 SMAP satellite product description

2019年5月至2020年5月北太平洋部分海域(135°～165°E,15°～45°N)共2 057 400组SMAP卫星V4.0L2C SSS反演数据和辅助数据源自Remote Sensing System[16]网站。SMAP卫星盐度反演产品有SSS_SMAP_40 km和SSS_SMAP_70 km两种,其中SSS_SMAP_40 km是在卫星原始40 km空间分辨率下经过误差修正的数据;而SSS_SMAP_70 km是利用最近邻算法,将SSS_SMAP_40 km平滑至约70 km空间分辨率的数据,通常作为SMAP卫星科学应用的标准或默认产品。

1.3 数据匹配

由于实测数据与SMAP卫星数据存在时间和空间上的差异,按照Busalacchi等[17]提出的数据匹配原则,以24 h为时间间隔、0.5°×0.5°网格为空间间隔,将Argo浮标数据与相同时空下SMAP卫星数据进行匹配,最终确定576组完全匹配的有效数据。

2 方 法

2.1 参数选择与预处理

机器学习作为“黑箱”建模,对其输入的训练参数需要科学地选取。本研究通过计算SMAP L2C盐度数据与实测辅助参数之间的Pearson相关系数(表2)来选择反演参数。该系数可衡量数据集之间的线性关系,其绝对值越接近于1,表明数据间的相关性越强。计算结果表明:相比于其他参数,海表温度(Sea Surface Temperature,SST)、风 速(Wind Speed,WS)、大 气 总 透 过 率(Transmissivity,Tran)、降 雨 率(Rainfall Rate,RR)、海表亮温(Brightness Temperature,TB)与SSS之间存在较为显著的相关性,其显著水平均大于0.01,其中SST与SSS相关系数最高,达到0.562。该5项因子作为模型建立的输入参量,详细描述见表2。

表2 模型输入参量Table 2 Model input parameters

为消除不同单位指标的影响,保证输入参数在同一纲量上讨论,模型采用标准归一,使参数数值统一落到[0,1]区间。归一化后的参数值xnr计算公式为

式中:x为原始输入参数值,μ为所有输入参数的均值,σ为所有输入参数的标准差。

2.2 DNN模型反演方法

深度神经网络(DNN)是一种典型的人工神经网络(Artificial Neural Network,ANN),它通过模拟人类大脑神经结构和非线性处理进程,对大规模数据进行处理分析[18]。DNN模型结构包括输入层、隐藏层和输出层,各邻近层节点之间有连线而同层以及跨层节点之间无连线。该模型进行训练时,首先,输入层参数通过激活函数g(Z)对每个节点的连接权重系数w和偏置量b正向传播到隐藏层,然后输出到隐藏层的参数逐层继续正向传播至输出层,输出层通过梯度下降过程调节w、b使得损失函数L(w,b)最小,完成反向传播过程。这样迭代训练多次,最终使模型的预测值接近于与真实值(y)。

DNN模型结构如图1所示。该模型由5个输入参数,3层隐藏层和1个输出SSS组成。

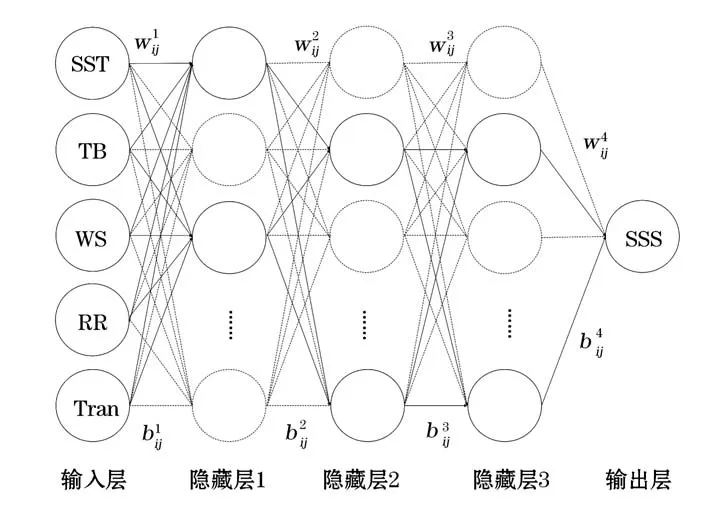
图1 DNN模型结构Fig.1 DNN model structure

2.2.1 正向传播过程

正向传播过程通过激活函数更新权重w和偏置b,每个节点之间都将进行一个线性过程和非线性过程。在整个数据集上表示为:

式中:Z(n)为激活前的输出,n为参数所在层数,w(n)为第n层权重矩阵,A(n-1)为n-1层输出,b(n)为第n层偏置。当n=1时,A(0)为输入层元素组成的矩阵。对于第n层输出层,A(n)为预测输出值,函数g为本层的激活函数。

2.2.2 反向传播过程

反向传播过程即利用梯度下降来降低损失函数L(w,b),缩小预测值与真实值(y)间的差距。损失函数在单个训练样本中定义,在整个训练样本中通常用成本函数J(w,b)、即m个训练样本的损失函数的算术平均值来表示:

本实验采用均方误差MSE(Mean Square Error)作为损失(Loss)函数,计算式为:

在整个数据集中,梯度下降通过对成本函数反向求导不断更新权重w和偏置b至最优解,公式如下:

式中,a为设置的学习率,为成本函数对w和b的偏导。

2.3 SVM模型反演方法

支持向量机(Support Vector Machine,SVM)作为一种多层感知机延伸下的浅层神经网络模型,通过引入核函数来代替高维空间中的内积运算,对训练集建立支持向量与待预测向量之间的非线性关系,以实现对测试集的预测,能够较好地解决非线性拟合问题。

该模型是由Vapnik等[19]提出的解决二分类问题的方法,将寻找正反两类间隔最大的最优超平面,归结为一个带约束的二次凸优化问题,其目标函数为[19]

式中,wT为权重系数矩阵;b为偏差;x i和y i分别为训练前后样本;ε为偏设误差;ζi与为松弛系数,约束条件≥0。公式中的优化问题转化为约束最小化问题,目标函数可以采用具有特殊结构的二次规划(Quadratic Programming,QP)的方法进行最小值求解,利用拉格朗日对偶(Lagrange Duality,DL)变换到对偶变量的优化问题,引入拉格朗日乘子消除约束项。同时,模型需要引入核函数将数据映射到高维空间,调整核参数gamma值以更好地拟合模型。

2.4 实 验

将时空匹配后的576组数据集按8∶2的比例划分为训练集和测试集,以SMAP卫星V4.0 L2C产品5项辅助参量:海表温度(SST)、风速(WS)、大气总透过率(Tran)、降雨率(RR)和海表面亮温(TB)为输入要素,Argo实测数据的SSS为输出要素。反演流程如图2所示。

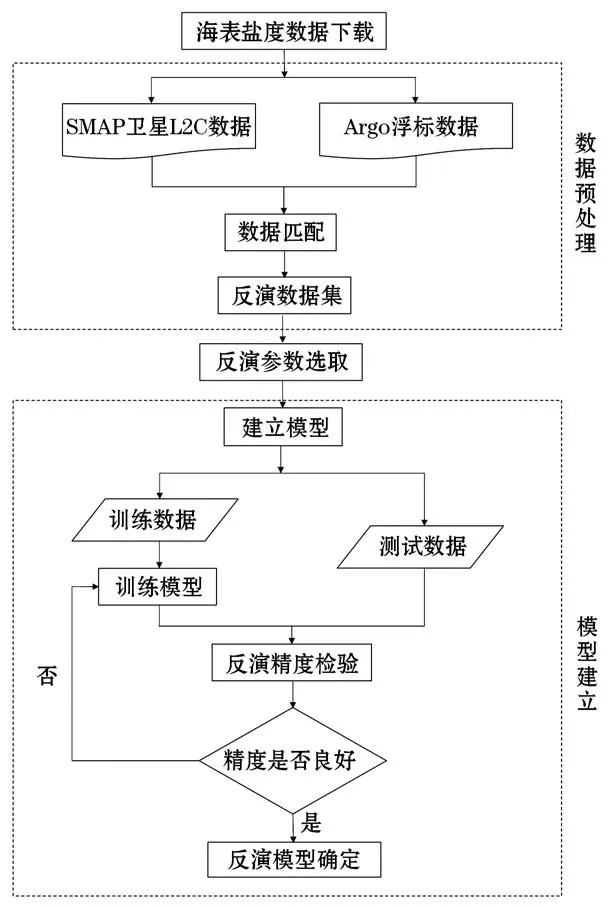
图2 2种模型的海表盐度反演流程Fig.2 Sea Surface Salinity(SSS)inversion flow of two models

DNN常用的激活函数Sigmoid函数和tanh函数容易发生导数趋近于0的情况,使得梯度下降变慢[20]。因此,本模型选用ReLU函数为激活函数,以确保训练速度。为防止由于训练样本较少导致的过拟合问题,本研究借助Krizhevsky等[21]于2012年提出的Dropout算法,按照一定概率p将神经元随机失活,实验选取p为0.5。为进一步提高训练效率,模型采用了Adam优化器,能够修正从原点初始化的一阶矩和二阶矩估计,且相比RMSprop算法,Adam优化器能够修正偏置,保证每一次迭代学习率动态调整后都有确定范围。本实验设置初始学习率0.01,当测试集误差损失下降缓慢时,将学习率做(1/2)n衰减,使之最终降低至0.00 125。实验具体参数配置如表3所示。建立SVM模型时,采用与DNN模型同样划分的数据集,以径向基函数(Radial Basis Function,RBF)为核函数,利用网络搜索法不断调整参数gamma和惩罚因子C的取值,最终确定模型最优值gamma为0.01,C为1 000。

表3 DNN模型参数设置Table 3 Parameters setting of DNN model

3 结 果

将Argo实测数据、最优参数训练的DNN模型、RBF-SVM模型反演结果与SMAP卫星自身产品SSS_SMAP_70 km和SSS_SMAP_40 km数据进行对比,如图3所示。结果表明DNN模型与RBF-SVM模型反演盐度与Argo实测数据之间的吻合度较高,而SMAP产品SSS_SMAP_70 km和SSS_SMAP_40 km虽与实测数据的摆动趋势基本一致,但上下波动较大(图3a)。同时,以Argo实测数据为参考,DNN模型与RBF-SVM模型反演盐度的平均绝对误差MAE大多分布在0误差线附近,相比SMAP卫星的2种产品数据的误差要小得多(图3b)。

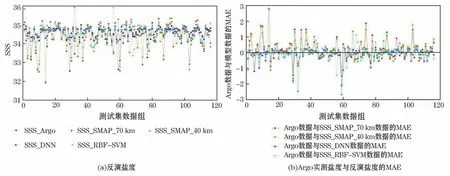
图3 反演盐度及Argo实测盐度与反演盐度的平均绝对误差Fig.3 Inversion result of SSS and its MAE from the Argo data

统计发现,DNN模型与RBF-SVF模型反演盐度的MAE(图4)在[-0.5,0.5]的数据各有109组和105组,分别占测试集总数的93.97%和90.52%,而SMAP自身产品SSS_SMAP_70 km和SSS_SMAP_40 km的MAE在[-0.5,0.5]的数据仅占测试集总数的71.55%和69.83%。此外,DNN与RBF-SVM模型反演盐度的MAE都在[-1,1]区间,而SSS_SMAP_70 km、SSS_SMAP_40 km的MAE分别有10.34%和16.38%超出了[-1,1]区间。综上所述,本文提出算法的反演盐度质量明显优于SMAP卫星自身产品质量。

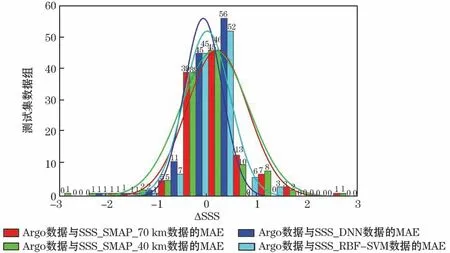
图4 Argo实测盐度与反演盐度的平均绝对误差Fig.4 Histogram of the MAE between the SSS inversion and the Argo data

将Argo实测盐度、DNN模型反演盐度、RBF-SVM模型反演盐度与SMAP卫星产品SSS_SMAP_70 km和SSS_SMAP_40 km通过克里金插值法绘制到研究区域的经纬度范围内,结果如图5所示。分析Argo实测数据的分布(图5a)发现,海表盐度在研究区域从北至南呈近似递增趋势,最高盐度分布在(160°～165°E,20°～25°N)范围内,最低盐度分布在(145°～150°E,40°～45°N)范围内。DNN模型与RBF-SVM模型的反演盐度分布模式与Argo实测数据相似,同样表现出从北至南分层递增的特征,并且具体的盐度极值区域与Argo数据之间出入不大,在实际使用允许的误差范围之内。相比较而言,SMAP卫星的2种产品SSS_SMAP_70 km和SSS_SMAP_40 km的盐度分布模式与Argo实测数据之间的吻合度较低,同时SSS_SMAP_40 km数据还表现出了整体略高于实测盐度值的不利趋势。

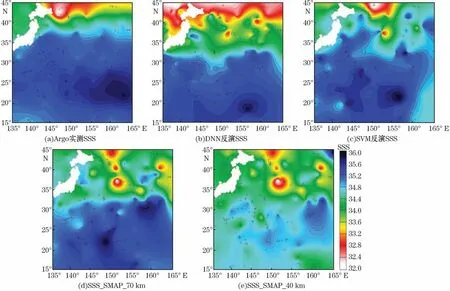
图5 Argo实测盐度、模型反演盐度及SMAP卫星盐度产品的分布模式Fig.5 Distribution of the Argo SSS,the SSS inversion and the SMAP products

为定量评价反演结果,本文采用了5种精度评价指标,分别是均方根误差(RMSE)、平均绝对误差(MAE)、最大绝对误差、最小绝对误差和相关系数(R)。其中前4项指标体现了模型对测试集的反演结果与Argo测量值之间的差异,其绝对值越接近于0代表精度越高。R值可表征反演值与Argo测量值之间的线性相关程度,其值越接近于1,相关性越强。本文DNN模型反演盐度、RBF-SVM模型反演盐度与SMAP卫星的2种产品SSS_SMAP_70 km和SSS_SMAP_40 km数据的各项精度指标如表4所示。分析发现,DNN模型和RBF-SVM模型反演盐度的各项误差都明显低于SMAP卫星的2种产品数据,同时,前两者的最大绝对误差和最小绝对误差也低于SMAP卫星的2种产品数据,说明2种反演模型数据都具有较高的稳定性。再比较各个盐度数据的R值,DNN模型和RBF-SVM模型的反演盐度都超过0.8,明显高于SSS_SMAP_70 km和SSS_SMAP_40 km的R值,这说明反演数据与实测值之间的线性相关性也超过了SMAP自身产品,充分体现了本文提出方法的优越性。

表4 反演模型与Argo实测数据的误差统计Table 4 Error statistics between inversion models and Argo measured data

4 结 语

为提高SMAP卫星海表面盐度产品精度,本文建立了DNN模型和RBF-SVM两种机器学习模型用于SMAP卫星盐度反演。其中,深度神经网络DNN具有多节点、多隐藏层,无需依赖传统物理机制进行反演,而支持向量机RBF-SVM模型适用于小样本问题。比较两组实验结果与Argo实测数据之间的均方根误差RMSE、平均绝对误差MAE、最大绝对误差和最小绝对误差发现,DNN模型反演数据的各项误差均稍低于SVM模型。总体来说,本文建立的2种方法均能够生成明显优于SMAP卫星自身产品的海表面盐度数据,其产生的盐度分布模式图也与Argo实测盐度分布模式图接近,充分体现了本文方法的有效性,研究结果能够为相关学科提供数据支撑。

考虑到训练样本有限,实测数据与SMAP卫星L2C数据在时空匹配中具有一定误差,且模型输入层参数的选取数量和合理性仍需考量,因此本文模型还有更多的完善空间。在未来的研究中,应加大训练样本数量,对输入层参数和模型训练参数进一步优化调整,同时选择不同海域作为研究对象,争取在提高模型精度的同时还能更好地适用于全球海域。