利用Fallback的在线服务信誉防控制机制
2022-02-19付晓东刘利军
李 方,付晓东,2,岳 昆,刘 骊,刘利军,冯 勇
1(昆明理工大学 信息工程与自动化学院,昆明 650500) 2(昆明理工大学 云南省计算机技术应用重点实验室,昆明 650500) 3(云南大学 信息学院,昆明 650091)
1 引 言
随着互联网应用的飞速发展与进步,传统商业环境发生了巨大的改变,以互联网为媒介向用户提供在线服务在企业中得到快速普及,成为企业运行的发展趋势和必然选择[1].在线服务是指利用互联网技术,向用户提供线上服务的方式.在线服务给人们的日常工作生活带来了巨大的便利,利用这种技术,用户可以进行数据共享、完成信息交换、购买商品和服务等[2].用户与在线服务进行交互后,依照主观感受对服务做出评价,表达他们的偏好及满意程度[3].通过聚合用户群体的偏好信息获得服务信誉,可帮助用户群体在具有相似功能的在线服务中选择出满足用户需求的服务.
在线服务信誉是用户对在线服务的信任程度,对于在线服务选择起着重要的作用[4].客观、有效的在线服务信誉度量方法在帮助用户选择优质的在线服务和提升在线服务质量方面具有重要的应用价值[5].为了提高自身影响力或者降低对手影响力,恶意用户或者在线服务提供商可能操纵、攻击信誉系统,扭曲在线服务的信誉,致使用户利用这种信誉进行服务选择时会产生不客观的结果,从而使用户面临无法选择到满足需求服务的风险[6].恶意用户对信誉系统的攻击通常具有欺骗性、合谋性或战略性,误导买家与服务进行交易[7,8].这其中有一类特殊的群体,就是信誉系统的管理者,他们掌握了普通用户的偏好,为获取不当利益,可以通过删除或者增加用户、服务以使特定服务成为信誉最高的服务.
现有工作重点关注普通用户或者在线服务提供者对信誉的操纵,而缺少通过技术手段防范信誉系统管理者对服务信誉进行控制的措施.为此,本文提出利用Fallback的在线服务信誉防控制机制.该机制通过提高控制用户偏好策略的计算复杂性,将在线服务信誉控制建模为判断某一服务是否能通过控制成为信誉最高的服务的问题.理论证明利用Fallback的在线服务信誉控制的问题是固定参数不可解的,即利用Fallback的用户偏好控制问题是具有抵抗力的(Resistance)[9],从而利用Fallback的信誉系统难以被控制.
2 相关工作
随着电子商务的快速发展,用户获取线上服务变得越来越方便,但信用缺失问题也越来越严重.虽然电子商务系统设置了信誉排名和推荐机制,为用户在选择诚信服务方面提供辅助的决策支持.然而,一些恶意用户、在线服务提供商不断采取欺骗、伪装、漂白、共谋、歧视等策略控制用户偏好,进而误导用户进行服务选择[10,11].
总结现有的在线服务信誉系统防控制机制,主要包括4方面:减轻通过虚假信息进行操纵的影响;识别恶意用户,对他们做出惩罚或者进行隔离;激励用户表达真实偏好;增加控制者的控制成本(成本可能是金钱、时间等).
减轻通过虚假信息进行操纵的影响来防控制比较常见.Anupama Aggarwal建立了检测用户对信誉系统操纵行为的机制,利用可疑用户的时间行为和网络特征,可以从合法用户中检测出虚假操纵行为,减轻操纵信誉对在线社交网络的影响[12].Jaehong Ahn等提出从存储在基于区块链的在线支付系统交易的原始评价中获取信誉[13],防止信息被恶意操纵.
识别恶意用户,对他们做出惩罚或隔离方面,Xin Wang等基于印象理论,提出了一种由最近邻搜索算法及分类算法组成的无监督策略,隔离诚实和不诚实的用户及服务[14].Nitin Kumar Saini等提出了一种针对共谋检测的反应性解决方案,并针对检测到的恶意用户提出了降低其声誉的惩罚策略[15];马述忠等基于网络店铺销售假冒行为,构建了不完全信息的动态博弈模型,考察了惩罚机制和信誉机制的治理效果[16].
激励用户表达真实偏好方面,Junsheng Chang等提出了一种基于政策的公平差别化服务激励机制,定义了参与水平和推荐可信度这两个参数,识别了信誉系统中用户的行为特征[17].基于上述两个参数,还提出了一个简单而有效的信誉信息交换协议,以激励用户诚实的表达真实偏好;Ali Ghaffarinejad等针对面向服务的环境,提出了一种基于多个特殊信誉中心的分布式信誉机制[18].该机制具有抗共谋的能力,并激励企业资信管理人员尝试全面收集信誉信息并如实报告;Yingtao Xu等基于信誉评价的动态特性,提出了一种基于最优控制问题的在线信誉动态反馈激励模型[19].
增加控制者的控制成本方面,Kevin Hoffman等提出的抗Sybil攻击的解决方案分为集中式和分布式两种[20].在集中式方法中,中央权威机构发出和验证每个实体唯一的凭证.为了增加获得多个身份的成本,中央权威可能需要为每个身份支付货币或计算费用;Bhupender Kumar等通过设置身份节点在网络中保持可信的全局信任阈值,增加控制成本来阻止攻击[21].
上述研究中对于信誉系统的防控制对象都是使用信誉系统的普通用户或在线服务提供者.然而对信誉系统内部的管理者来说,他们更容易掌握用户信息,可以根据掌握到的用户偏好对当前的用户、在线服务进行增加、删除等操作对服务信誉进行有针对性的操纵,使信誉系统面临被其管理者操纵的道德风险.为此,本文考虑了掌握所有用户偏好的信誉系统管理者的易控制性,利用了社会选择理论中的方法,提出了一种利用Fallback的在线服务信誉防控制机制.最后通过理论分析和实验验证了方法的合理性和有效性.
3 问题描述
3.1 问题定义
对信誉系统的控制可分为构造性控制和破坏性控制,并且两种控制类型都通过增加和删除用户或服务进行控制.构造性控制作为一种最经典且最常见的控制[22],不失一般性,本文重点阐述构造性控制问题.为了更好地阐述利用Fallback的在线服务信誉防控制的问题,本文首先给出相关定义如下:
定义1.集合U={ui|i=1,2,…,n}为所有用户集合;集合S={sj|j=1,2,…,m}为用户产生交互的所有服务集合.其中,n为用户的个数,m为在线服务的个数.
定义2.评分向量ri=(ri1,ri2,…rij,…,rim)表示用户ui对所有服务的评分信息,rij表示用户ui对服务sj的评分,说明用户ui对服务sj的满意程度.评分采用电子商务评价机制中常用的5个评分等级,1-5分别表示很不满意、不满意、一般、满意和很满意.所有用户对服务的评分信息用矩阵R=[rij]m×n表示.
由于在线服务规模非常庞大,用户不可能对所有服务进行评分.目前,协同过滤方法已被广泛地用于信誉系统,该方法通过寻找与自己偏好相似的用户进行评分预测.为此,可采用Fernández-Tobías I等人提出的协同过滤方法[23]对评分进行填充.
定义3.服务集S的信誉用信誉向量rp=(rp1,rp2,…rpj,…,rpm)表示,rpj为服务sj的信誉值.根据用户对在线服务的评分R采用不同的信誉度量方法可以得到在线服务的信誉rp.
定义4.管理者对在线服务信誉控制的问题可表述为f:O→sj,sj∈S,其中sj为信誉最高的服务,集合O为所有用户的序数偏好.即管理者通过对所有用户对在线服务的偏好O实施控制使服务sj成为信誉最高的服务.
管理者对在线服务信誉控制问题具体可分为增加用户构造性控制问题、删除用户构造性控制问题、增加服务构造性控制问题和删除服务构造性控制问题.
定义5.增加用户构造性控制问题:给定用户偏好集合O,实施控制前的初始用户集合U1、增加的干扰用户集合U2(U=U1∪U2,U1∩U2=Ø),控制后信誉最高的服务sj∈S,基于用户群体偏好O通过增加干扰用户U2使得服务sj成为信誉最高的服务.
即信誉系统管理者利用掌握到的用户偏好,通过增加干扰用户使得实施控制前的某一特定服务成为信誉最高的服务.
定义6.删除用户构造性控制问题:给定用户偏好集合O,实施控制后信誉最高的服务sj∈S,基于用户群体偏好O通过删除用户集U中k个用户使得服务sj成为信誉最高的服务.
即信誉系统管理者利用掌握到的用户偏好,通过删除用户使得某一特定服务成为信誉最高的服务.
定义7.增加服务构造性控制问题:给定用户偏好集合O,实施控制前的初始服务集合S1、增加的干扰服务集合S2(S=S1∪S2,S1∩S2=Ø),控制后信誉最高的服务sj∈S1,基于用户群体偏好O通过增加干扰服务S2使得服务sj成为信誉最高的服务.
即信誉系统管理者利用掌握到的用户偏好,通过增加干扰服务使得实施控制前的某一特定服务成为信誉最高的服务.
定义8.删除服务构造性控制问题:给定用户偏好集合O,实施控制后信誉最高的服务sj∈S,基于用户群体偏好O通过删除服务集S中k个服务使得服务sj成为信誉最高的服务.
即信誉系统管理者利用掌握到的用户偏好,通过删除服务使得某一特定服务成为信誉最高的服务.
因此,本文旨在解决通过增加、删除用户或服务的构造性控制问题,防止信誉系统内部的管理者将某特定服务控制为信誉最高的服务,干扰用户的选择.
3.2 举例说明
例.以常见的均值法增加用户的构造性控制问题为例.假设有用户集U={u1,u2,u3,u4,u5},u5是增加的干扰用户,服务集S={s1,s2,s3,s4},用户-服务的评分矩阵R如表1所示,需解决基于用户对服务的偏好信息通过增加用户使得服务s2成为信誉最高服务的问题:
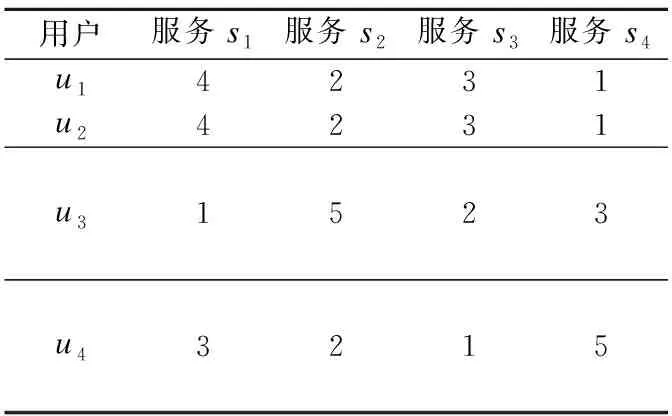
表1 用户-服务评分表Table 1 User-service score sheet
由表1可见,通过计算所有用户对服务评分的平均值得到其服务信誉,得到的信誉向量为rp=(3,2.75,2.25,2.5),s1为当前信誉最高的服务.通过增加干扰用户u5后的用户-服务评分表如表2所示.

表2 用户-服务评分矩阵表Table 2 User-service score sheet
增加干扰用户u5后得到的信誉向量为rp=(2.8,3.2,2.4,2.8).通过增加用户控制,使得服务s2成为了信誉最高的服务.因此通过增加用户可以很容易地对均值法实施构造性控制.本文提出Fallback方法进行在线服务信誉度量,以解决信誉系统内部的管理者利用掌握到的用户偏好,对服务信誉进行控制的问题.
4 利用Fallback的在线服务信誉防控制机制
Fallback方法是Bucklin与Approal混合的社会选择方法[24].Bucklin方法中每个用户要根据他的偏好对所有的服务进行严格的线性排序;Approal方法中用户通过批准向量(0,1)表达偏好,0代表不赞同,1代表赞同.Fallback将Bucklin和Approal结合起来,每个用户提供对他所认可服务的严格偏好排序.目前已知的社会选择方法中,Fallback方法显示了最广泛的控制抵抗力[9].因此,本文利用Fallback,设计了一种在线服务信誉防控制机制,利用Fallback控制用户偏好问题的计算复杂性高的特性来防止管理者控制信誉.
4.1 利用Fallback的在线服务信誉度量
本文信誉度量方法的核心是根据所有用户对在线服务的偏好获取满足Fallback绝对多数阈值条件的在线服务信誉向量.
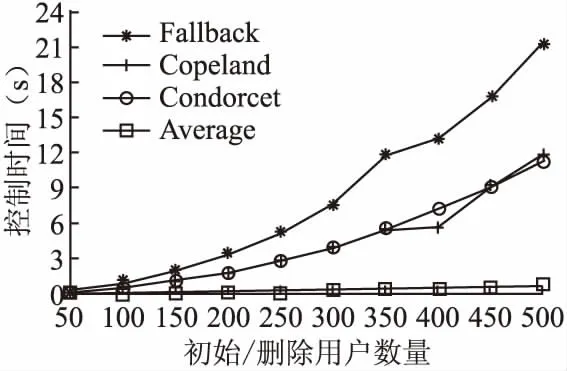
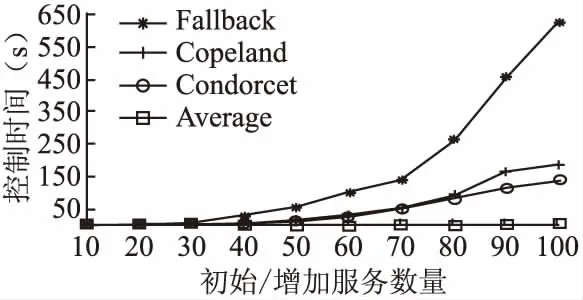
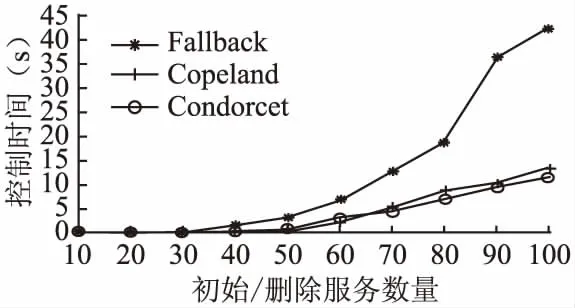
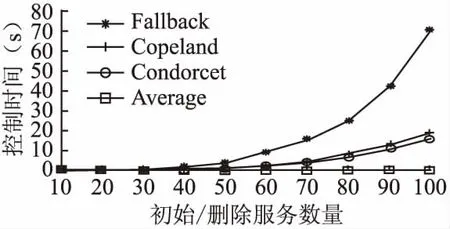
定义9.用户ui对在线服务的评分rij越大表示ui对sj越满意,rij>rik表示用户ui认为服务sj优于服务sk(记作sj≻isk);rij 首先根据用户ui对在线服务的评分信息ri,将每个用户对在线服务的评分按大小进行排序,若在线服务对应的评分相同则采用随机法对评分相同的服务进行排序,获取所有用户的序数偏好集合.例如,对于表1中用户u1的评分信息为r1=(4,2,3,1),对4个服务分数进行排序可以得到用户u1对在线服务的偏好序β1:s1≻1s3≻1s2≻1s4. 若用户提供了对在线服务的偏好排序,则可直接使用该排序作为用户偏好O.由于用户不可能对所有服务进行偏好排序,即用户偏好序是不完全序.为此,可采用William Webber[6]、Riku Togashi等提出[25]的概率用户模型,处理不完整偏好排序,从而得到一个完整偏好排序. 获取所有用户对在线服务的偏好排序后利用Fallback方法计算信誉向量,得到最终所有用户对服务的信誉度及最终的用户群体偏好.首先需要得到在线服务在偏好排序中的l级分数.基于所有用户的序数偏好集合O,计算每一个在线服务sj∈S在偏好排序中的l级分数scorel(sj),其表示将在线服务sj排在前l位的用户的数量,l=1,2,…,n. 定义10.函数Di的取值为0、1:若用户ui认为服务sj优于sk,即sj≻isk则Di(sj≻isk)=1、Di(sk≻isj)=0;认为sk优于sj,则Di(sk≻isj)=1、Di(sj≻isk)=0. 定义11.函数Mi的取值为0、1,可以表示为: (1) 最终服务sj在偏好排序中的l级分数scorel(sj)为: (2) 比如,根据表1的评分信息得出偏好排序,没有用户将在线服务s3排在第1位,所以服务s3的1级分数为0;用户u1、u2将在线服务s3排在前2位,所以服务s3的2级分数为2;用户u1、u2、u3将在线服务s3排在前3位,所以服务s3的3级分数为3.同理我们也可以分别计算出其余在线服务的l级分数,最终得到l级分数scorel(sj)如表3所示. 表3 服务的l级分数表Table 3 Level l score of services sheet 得到在线服务在偏好排序中的l级分数后,需要判断这些分数是否满足绝对多数阈值条件.用户集U中的用户的绝对多数阈值为: maj(U)=|U|/2+1 (3) 1)根据在线服务在偏好排序中的l级分数,判断第一级中是否有达到scorel(sj)≥maj(U)条件的服务; 2)若有,则该服务的信誉值即为当前满足绝对多数阈值条件的一级分数; 3)若没有达到条件,判断下一级分数中是否存在满足条件的服务,直到得到每个服务的信誉值. 最先达到绝对多数阈值条件的服务是用户群体偏好排名第1的服务,若在同一级分数中存在几个满足条件的服务,则对这些服务的分数进行排序从而得到最终的用户群体偏好.比如,表3中在第2级中服务s1的信誉是最先达到阈值3的,服务s2、s3的信誉都在第3级达到阈值3,服务s2的信誉4大于服务s3的信誉3,最终得到的信誉向量为rp=(3,4,3,4),最终的偏好排序为s1≻s2≻s3≻s4. 基于以上分析,最后确定出利用Fallback的在线服务信誉度量函数: f(sj)=scorel(sj),scorel(sj)≥maj(U) (4) 算法1给出了利用Fallback的在线服务信誉度量算法.其中Mi(sj)由公式(1)计算得出. 算法1.利用Fallback的在线服务信誉度量算法 输入:所有用户的序数偏好集合O 输出:在线服务信誉向量rp 2.fori=1 tondo 3.forj=1 tomdo 4.fork=1 tomdo 6.endfor 7.endfor 8.endfor 10.ifscorel(sj)≥maj(U) then 11.rpj=scorel(sj); 12.else if 13.l+1; 14. goto to (10); 15.fill the vectorrpbyrpj; 16.returnrp; 从上面描述可以看出,算法1中第2行-第4行的for循环表示每个用户都对服务sj与除sj以外的其他服务逐一进行比较,其时间复杂度为O(nm2),最终算法1的时间复杂度为O(nm2). 为了通过理论验证本方法防控制的有效性,下面对利用Fallback的在线服务信誉度量方法的防控制性进行证明. 防控制性表明Fallback控制用户偏好问题的计算复杂性高,即证明构造性控制问题是固定参数不可解的.本文以利用Fallback的删除服务构造性控制问题为例,证明该控制问题固定参数不可解,首先给出参数化问题[26]相关定义如下: 定义12.参数化问题分为固定参数可解(fixed- parameter tractability,FPT)和固定参数不可解.FPT:给定利用Fallback的删除服务构造性控制问题Π′,如果有一个算法在运行时间O(g(k′)|I|O(1))内可以解决该问题,则该问题称为固定参数可解,其中k′为最多删除服务的个数,g是任意函数,(I′,k′)是删除服务构造性控制问题的实例即利用Fallback的在线服务集S中服务的信誉度量.否则利用Fallback的删除服务构造性控制问题Π′被称为固定参数不可解. FPT-归约:如果存在一种算法,可以在时间O(g(k)|I|O(1))内,把k-支配集问题Π的实例(I,k)转换为利用Fallback的删除服务构造性控制问题Π′的实例(I′,k′),则k-支配集问题Π可FPT-归约到删除服务构造性控制问题Π′.其中k为k-支配集的参数k,k′为最多删除服务的个数,在定理1中k=k′,g是任意函数. 定义13.参数化问题Π可FPT-归约到WCNF-2SAT问题,那么称Π属于W[1];参数化问题Π可FPT-归约到WCS[t]问题,那么称Π属于W[t].WCS[2]问题是WCNF-2SAT问题的拓展.W[1]⊆W[2].一个问题如果是W[t]-hard问题,则被认为是固定参数不可解的. 即只需要找到一个已知的W[2]-complete问题k-支配集Π的实例可以转换到利用Fallback的删除服务构造性控制问题Π′的实例则可证明该构造性控制问题是W[2]-hard问题即固定参数不可解问题. 定理.利用Fallback的删除服务构造性控制问题是W[2]-hard问题. 证明:已知的W[2]-complete问题k-支配集问题:在一个无向图G=(B,E)中,对于子集B′⊆B,若每一个节点bi,bi∈B′或邻接B′中至少一个点,则称子集B′为支配集. 给定k-支配集问题的实例I=(G,k),其中G=(S1,E),k 构造利用Fallback的删除服务构造性控制问题的实例I′:给定用户集U、服务集S,其中S=S1∪S2∪{sj}∪S3∪S4,sj是控制后信誉最高的服务. S2:S2是一组k+1个服务,这些服务防止删除最多k个服务使服务sj成为唯一的信誉最高的服务. S4:S4是一组n(k+1)个服务,对于每个j,1≤j≤k+1,可以找到具有n个元素的子集S4j⊆S4,这些子集确保每个服务s2j∈S2总是位于表4的第2个偏好排序的第(n+k+1)个位置. U是2n+1个用户集合,因此n+1为绝对多数阈值.用户集U中的用户对服务集S中服务的偏好排序如表4所示. 表4 用户-服务偏好排序表Table 4 User-service preference ranking sheet 服务的l级分数如表5所示: 表5 服务的l级分数表Table 5 Level l score of services sheet 证明实例I可以转换到实例I′,即需要证明下面结果是成立的:实例I存在大小为k的支配集当且仅当实例I′中通过删除k个服务使sj成为唯一的信誉最高的服务(这里k-支配集的参数k与最多删除k个服务的k相同). 从右到左:假设sj可以通过删除最多k个服务而成为唯一的信誉最高的服务.由于除了sj之外(即S2中的服务),还有k+1个服务在第n+k+1级达到绝对多数,从S2中删除k个服务不足以使sj成为最终的唯一的信誉最高的服务.因此sj必须在低于或等于n+k级上才能成为唯一的信誉最高的服务,那么在表4中sj在第一个偏好排序中的排名至少向前一个位置才有可能,这说明k′≤k个被删除的服务可能: 1.全被包含在S1中并且对应G中的一个k′大小的支配集. 2.都在S1∪S3中. 证明过程表明已知的W[2]-complete问题k-支配集可以FPT-归约到利用Fallback的删除服务构造性控制问题,因此利用Fallback的删除服务的构造性控制问题是W[2]-hard问题即该控制问题是固定参数不可解的,说明Fallback的删除服务的构造性控制问题的计算复杂性高.同理,要证明其余构造性控制类型问题是NP-hard/W[2]-hard问题也可以通过找到已知的NP-complete/W[2]-complete问题归约到控制问题来证明. 为验证Fallback的防控制性,设计实现相关实验并对实验结果进行分析.实验环境为Intel Core i7 处理器,8G内存,64位Windows 10操作系统,开发环境为pyCharm 2019.1,开发语言为 Python 3.7. 为了避免实验的偏向性,使实验更加真实和可靠,实验同时采用合成数据集和真实数据集.合成数据集使用Mallows模型生成[27];真实数据集为MovieLens数据集[28]. Mallows模型在序数偏好研究中被广泛认可并应用[27],其合成的偏好数据集用ML表示.在Mallows模型中设置两个参数:中心偏好序σ和离散参数θ.其中,σ为由m个在线服务构成的完整偏好排序,离散参数θ用于控制合成的偏好序与中心偏好序σ的离散程度.本文随机生成中心偏好序σ,离散参数θ设置为0.5,设置较大数量的用户量n及在线服务量m,合成不同的偏好数据集. MovieLens数据集在服务研究的相关领域内得到普遍应用[28],该数据集包含了1682部电影,943个用户,以及 100000 条左右的评分(1~5),每个用户至少对 20 部电影进行过评分,用MV表示.由于MV中用户对服务的评分非常稀疏,首先采用协同过滤方法对评分进行填充,然后根据每个用户对服务的评分进行排序,若评分相同则采用随机法对其进行排序,最终获得用户-服务完整偏好排序. 为了在最容易控制的情况下测试各个方法的防控制性,实验通过使用预先排序,找到控制的最优策略.即对增加用户构造性控制来说,先增加将想控制服务排在最好位置的用户;对删除用户构造性控制来说,先删除将想控制服务排在最差位置的用户;对增加服务构造性控制来说,先增加对想控制服务威胁最小的服务;对删除服务构造性控制来说,先删除对想控制服务最具威胁的服务.在最能满足控制要求的情况下,测试控制成功所需的时间.控制成功所需的时间越长,说明方法的防操纵性越强. Felix Brandt等指出Copeland方法是已知的第一个完全抵制所有类型的构造性控制的方法[22];Condorcet方法是控制用户偏好问题研究的第1个方法,所以在Mallows模型中本文使用Copeland和Condorcet方法作为与Fallback的对比方法.基于Mallows模型的实验对4种控制类型进行实验,增加/删除用户的构造性控制、增加/删除服务的构造性控制. 由于均值法(Average)易于理解并且被广泛的应用于在线服务信誉系统中[4],所以在MovieLens数据集上的实验对比方法除了Copeland和Condorcet方法之外多增加了均值法(Average).基于MovieLens数据集的实验同样对上述4种控制类型进行实验. 在增加/删除用户或服务的场景中,设置增加/删除用户或服务的数量与初始用户或服务的数量相同大小[9]. 5.2.1 增加用户和删除用户的构造性控制 在增加用户的构造性控制中,实验对新增用户进行预排序,找到增加用户的构造性控制的最优策略,在最易控制的情况下测试各个方法的防控制性.首先增加的用户是将想控制的服务排在最好位置的用户,最后增加的用户是将服务排在最差位置的用户.删除用户的预排序过程与增加用户的预排序过程相反.由于ML数据集中的用户直接提供对在线服务的偏好排序,而均值法需要根据用户的评分信息得到服务的信誉,所以在基于ML数据集的实验中未使用均值法(Average)作为对比方法. 基于ML数据集的增加用户构造性控制实验模拟了控制前的50-500个初始用户、50-500个增加的干扰用户和10个在线服务.由于MV数据集的用户总量为943个,基于MV数据集的增加用户实验模拟了50-450个初始用户、50-450个增加的干扰用户和10个在线服务,两个实验增加用户量与初始用户量相同.实验记录Fallback方法及对比方法的控制成功所需的时间.ML增加用户构造性控制成功所需的时间如表6所示,MV控制成功所需的时间如图1所示. 表6 ML数据集增加用户构造性控制时间表Table 6 Time of constructive control by adding users in ML data sets sheet 图1 MV数据集增加用户构造性控制时间Fig.1 Time of constructive control by adding users in MV data sets 在删除用户的构造性控制中,基于ML、MV的实验模拟了50-500个用户和10个在线服务,最多可以删除的用户量与初始用户量相同.ML删除用户构造性控制成功所需的时间如表7所示,MV控制成功所需的时间如图2所示. 表7 ML数据集删除用户构造性控制时间表Table 7 Time of constructive control by deleting users in ML data sets sheet 由表6、表7、图1、图2可见,随着增加的干扰用户或删除用户的数量增加,Fallback方法、Copeland方法、Condorcet方法、均值法(Average)的控制成功所需的时间均增加,Fallback方法控制时间比另外3种方法更长,Copeland方法、Condorcet方法控制时间比较接近,均值法(Average)控制时间最短.对 图2 MV数据集删除用户构造性控制时间Fig.2 Time of constructive control by deleting users in MV data sets 于较大数量级的用户来说,Fallback方法的防控制性优势更明显,通过增加用户或删除用户的构造性控制更为困难. 5.2.2 增加服务和删除服务的构造性控制 增加服务的构造性控制中,实验对新增服务进行预排序,找到增加服务的构造性控制的最优策略,预排序首先增加的第1个服务为:有最少的用户将该服务排在想控制的服务之前;最后增加的服务为:有最多的用户将该服务排在想控制的服务之前,即通过将服务升序排序之后,首先增加了对控制服务威胁最小的服务,找到了当前控制的最优策略.删除服务构造性控制的预排序过程与增加服务构造性控制的预排序过程相反,需要首先删除对控制服务成为唯一赢家最具威胁的服务.基于ML、MV数据集的增加服务构造性控制实验模拟了控制前10-100个初始服务、10-100个增加的干扰服务和10个用户,两个数据集的实验增加服务量与初始服务量相同.实验记录Fallback方法及对比方法的控制成功所需的时间.ML数据集增加服务构造性控制成功所需时间如图3所示,MV数据集控制成功所需时间如图4所示. 图3 ML数据集增加服务构造性控制时间Fig.3 Time of constructive control by adding services in ML data sets 图4 MV数据集增加服务构造性控制时间Fig.4 Time of constructive control by adding services in MV data sets 删除服务的构造性控制中,基于ML、MV的实验模拟了10-100个服务和10个用户.ML数据集删除服务构造性控制成功所需时间如图5所示,MV数据集控制成功所需时间如图6所示. 图5 ML数据集删除服务构造性控制时间Fig.5 Time of constructive control by deleting services in ML data sets 图6 MV数据集删除服务构造性控制时间Fig.6 Time of constructive control by deleting services in MV data sets 由图3-图6可见,随着增加的干扰服务或删除服务的数量增加,Fallback方法控制成功所需的时间呈指数型增长,当服务数量达到70个以上时,与其他方法的对比更加明显.Copeland方法、Condorcet方法控制成功时间比较接近,均值法(Average)控制成功时间最短.两种数据集的实验均表明,增加服务或删除服务构造性控制中,Fallback方法控制成功所需的时间最长,Fallback方法具有更强的防控制性. 本文提出了利用Fallback的在线服务信誉防控制机制,以解决信誉系统内部能够掌握用户偏好的管理者的控制问题.该机制通过Fallback方法集结所有用户的评分信息或偏好排序得到最终服务的信誉及用户群体偏好,利用Fallback方法提高控制用户偏好问题的计算复杂性,增加管理者的攻击时间成本以达到防控制的目的,为在线服务的防控制提供了一种新的思路.理论分析表明了该方法的防控制性,实验进一步验证了该方法防控制的有效性. 本方法在增加或者删除用户、服务的控制类型中验证了Fallback方法对指定服务的防控制性,但未对控制用户群体偏好序的防控制性进行验证.因此下一步的工作将针对各类控制的偏好序的防控制性进一步开展研究.
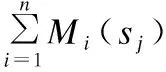


4.2 理论分析




5 实验结果及分析
5.1 数据集
5.2 防控制性实验




6 结 语
