相关性的ADC技术在超声波智能水表上的应用

1 相关性ADC的测量原理

1.1 时差法测量模型

时差法测量原理如图1所示，换能器安装方式采用插入式相互反射的布局，两个换能器中心距离为L，测量段管径为D。采样前端控制顺流方向换能器发射1MHz激励脉冲，则顺流到逆流方向超声波信号传播时间为Tup，同理逆流到顺流方向超声波信号传播时间为Tdn。其中Tup、Tdn可表示为[1]：

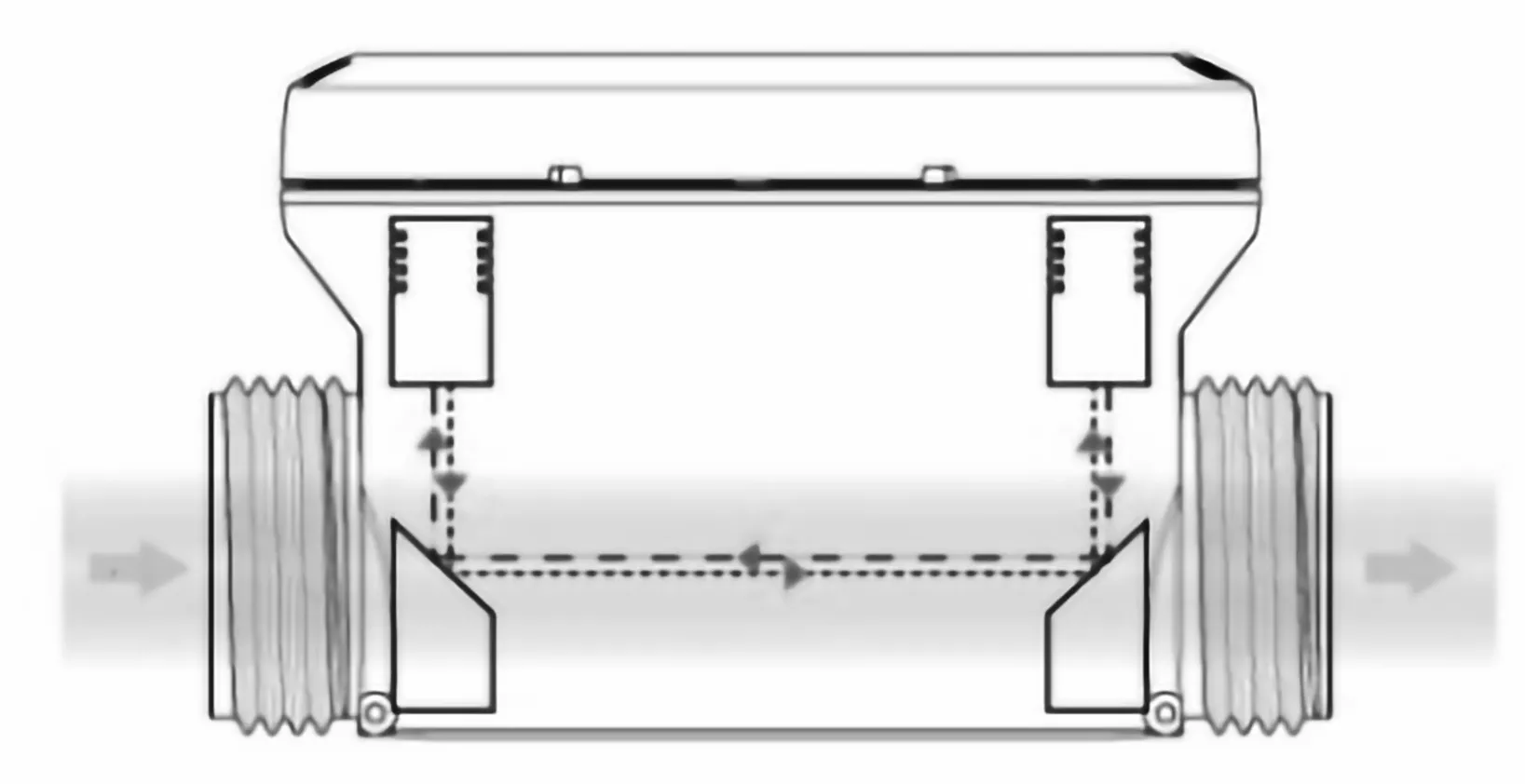
图1 时差法测量模型Fig.1 Time difference measurement model

1.2 互相关算法原理

采样前端分别控制顺、逆流方向换能器，获取顺流和逆流ADC采样序列值，分别用r1={r11,r12,r13,...,r1n}，r2={r21,r22,r23,...,r2n}表示，则：

其中fs表示ADC采样速率，i表示采样索引，序列中点的索引与采样周期的乘积即是该点代表的时间。

基于r1和r2，定义互相关函数R(k)，函数表示如下：

其中k={-m,-(m-1),...,m}，r1i,r2i=0(i＜1且i＞n)。找到R[k]的最大值点索引k'，k'=max(R(k))。对R(k'-1)、R(k'）、R(k'+1)进行余弦插值，找到插值后极值点对k'的偏移量：

图2 互相关性技术的ADC采样预估TOFFig.2 Estimation of TOF by ADC sampling based on cross correlation technique

2 硬件设计

2.1 采样前端设计

基于相关性的ADC技术中，通过采样前端控制换能器，发射激励脉冲信号，然后利用高速ADC采集顺、逆流回波信号并进行存储，通过自动增益器、低通滤波器对信号进行放大、滤波处理。然后使用相关运算器进行信号处理，并通过低功耗运算加速器进行数据处理，输出超声波在顺、逆流飞行时差和绝对飞行时间，采样框架如图3所示[2]：

图3 互相关性ADC框架Fig.3 Cross correlation ADC framework

使用ADC的方法与时间数字转化技术相比，互相关算法可以提供抑制噪声的低通滤波，可降低3～4倍的由噪音引起的标准差，减小线路噪声干扰。互相关算法对超声波回波信号的幅值、换能器间的性能差异变化不敏感，并可以根据测量信号幅值进行自动增益补偿，使得超声波水表使用寿命更长。高速ADC采样的应用，可以基于频域技术获取回波信号包络，根据包络变化特性进行换能器频率调整，可以降低不同工作温度下零点漂移，计量精度更高。

2.2 采样电路硬件设计

CH0_OUT和CH1_OUT是换能器驱动引脚，输出1MHz激励脉冲。CH0_IN和CH1_IN是回波接收引脚，模拟输入。R39、R51是驱动阻抗匹配，主要作用保证电信号能高效传输给换能器。C56、C58是回波信号耦合电容，考虑信号质量和耗能选择1nf电容。采样原理如图4所示：

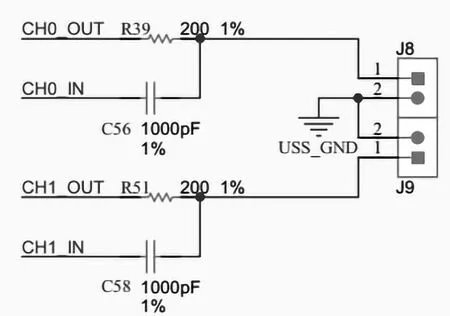
图4 采样原理图Fig.4 Sampling schematic diagram

PCB布线时遵从几点：(1)滤波退耦电容位置要合理，由滤波进，退耦出，退耦电容近量离芯片管脚要近，弱信号对电源的干净度要求比较高。(2)晶振尽量离芯片管脚近，切忌引线过长。(3)在超声波驱动和回波信号通道上，尽量减少过孔，过孔产生的寄生电容，容易影响信号接收时间，影响测量稳定性。(4)驱动和回波信号线尽量等长。(5)信号线路不可走线太长，以免引入共模干扰。

2.3 弱信号处理

（1）渐变式长期信号衰减：换能器表面结垢或不可逆变化导致信号衰减。这种情况可根据ADC采样值变化进行增益补偿。当检测到超声波信号ADC采样值衰减时，对回波信号进行自动增益调整，使超声波信号ADC采样值回归到合理范围内。（2）偶尔的电路或外界干扰以及气泡影响产生的信号衰减：这种情况主要采用数字滤波和补偿处理，通过历史数据对当前数据进行判断和补偿。当回波信号突然降低时，跟正常的历史数据相比有较大差异，如使用1MHz换能器会相差n个波形周期，补偿数据可以进行nus的线性补偿。

2.4 温度传感器

温度传感器用于测量水温，速度修正系数和雷诺数相关，计算雷诺数需要温度参数，通过温度计算或查表得到不同工况下水的粘度和密度。同时设计的超声波水表支持水温事件检测，根据设置的上、下限阈值，判断是否发生水温异常事件。测温采用热敏电阻（NTC），热敏电阻测温精度±0.5℃，并且成本相对于PT1000有较大优势。测温原理如图5所示：

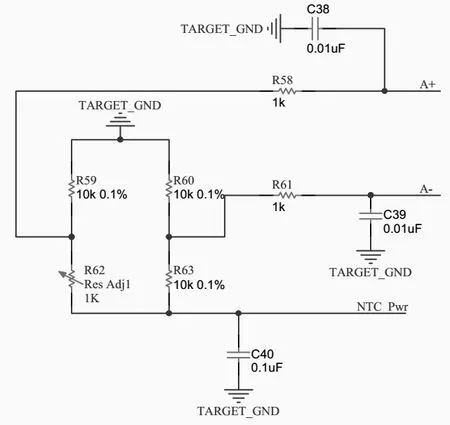
图5 测温原理图Fig.5 Schematic diagram of temperature measurement

为了降低功耗延长电池使用寿命，通过NTC_Pwr控制口对NTC进行电源控制，当时间计数达到测温周期，开启控制口，对A＋和A－两端进行电压采样，通过电压采样值计算温度。

3 流速修正

流体具有粘性，在同一个截面上不同径向位置流速不同，当靠近管壁时，流速较低；靠近管中心时，流速较高。同时流体的流动状态不同，也将呈现不同的速度分布。超声波测量出的流速是声道上的线平均速度vm，而计算流量所需是流过横截面的面平均流速。根据流体力学的半经验公式，线平均流速vm与面平均流速之关系为：,式中k为流体动力学修正系数。

当流体是层流状态（流体的雷诺数小于下临界雷诺数Re=2300）时，k=4/3。当流体为紊流状态（流体的雷诺数大于下临界雷诺数）时，k是以雷诺数Re为变量的函数，常用的经验公式为：当Re>1e5时k=1+0.01，当Re≤1e5时k=1+0.2488Re-0.125。

雷诺数公式Re=ρvd/μ，其中v、ρ、μ分别为流体的流速、密度与黏性系数，d为管道直径，雷诺数较小时，粘滞力对流场的影响大于惯性，流场中流速的扰动会因粘滞力而衰减，流体流动稳定，为层流；反之，若雷诺数较大时，惯性对流场的影响大于粘滞力，流体流动较不稳定，流速的微小变化容易发展、增强，形成紊乱、不规则的紊流流场，雷诺数小于2300的流动是层流，雷诺数等于2300～4000为过渡状态，雷诺数大于4000时的是湍流。

4 DN15超声波智能水表性能验证

4.1 性能指标

飞行时差精度:<100ps；时间测量分辨率:20ps；始动流量:3L/h；每秒1次采样耗能:4uA；计量精度:2级。

4.2 计量精度验证

用3只使用互相关性ADC技术实现的DN15超声波智能水表，在参比条件下进行误差验证，数据如表1所示：

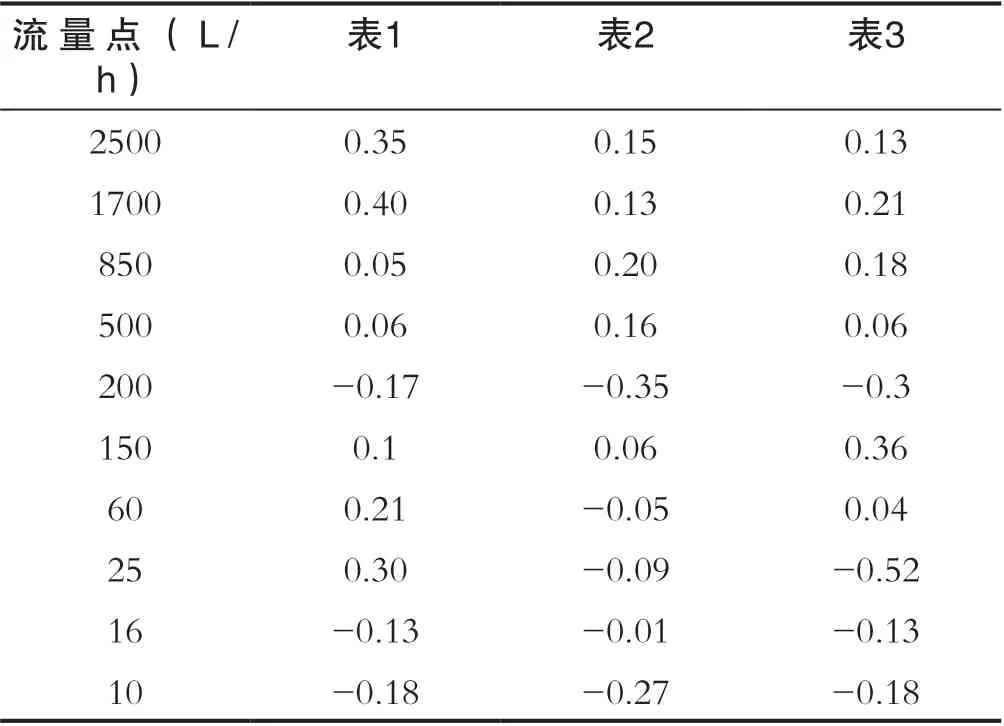
表1 计量精度验证Tab.1 Measurement accuracy verification

5 结论

与机械表相比，超声波水表有更低的始动流量、无机械磨损、计量精度高等优势。而超声波在应用中，小流量信号弱，容易受干扰；随着换能器性能老化，信号幅值也会降低，若变化不一致，会产生零点漂移。基于相关性ADC技术的超声波智能水表，具有更高的测量精度和量程范围，使用互相关理论，有效克服了以过零点来计算时差导致的计算结果的多样性和重复性差。