神经网络在高层建筑物沉降预测方面的应用

常州市新北自然资源和规划技术保障中心 佟国功

本文采集高层建筑物施工层数、沉降观测时间间隔和沉降值数据作为样本数据，训练神经网络。利用检验样本数据和多元线性回归模型对神经网络预测结果进行验证，通过分析比较证明Levenberg-Marquardt神经网络在高层建筑物沉降值预测方面的可行性。

施工期的高层建筑物，以及受地铁及地下空间施工影响的已建成的高层建筑物,都应进行沉降监测。沉降监测既可保障建筑物施工期间的安全,也可以为以后建筑设计、施工、管理和科学研究提供可靠的数据支持。

沉降数据回归预测分析方法有：多元线性回归分析法[1-2]、灰色模型法[3-4]、支持向量机法[1,3,5,6]、神经网络分析法[7-9]、深度学习法[10]等。本文以沉降监测时间间隔、建筑荷载（施工层数）为已知向量、沉降值为预测值，收集样本数据，利用Levenberg-Marquardt神经网络方法，进行沉降值预测分析。采用多元线性回归方法进行验证，通过比较分析发现：以高层建筑施工层数和沉降监测时间间隔为自变量、以沉降值为因变量时，Levenberg-Marquardt神经网络可以用于高层建筑物沉降值预测。

1 神经网络学习的实现

神经网络可以自动地从样本数据中学习到合适的权重参数，即通过输入及已知的输出反向求解出权重参数。神经网络采用分层结构，由输入层、中间层（多层）、输出层组成。神经网络只有相邻层节点之间的连接，同一层及跨层节点之间均无连接。神经网络通过正向传递实现模式识别、分类及回归分析，通过反向传播实现权重参数的自动获取，合适的权重参数是建立神经网络的基础。神经网络结构如图1所示。

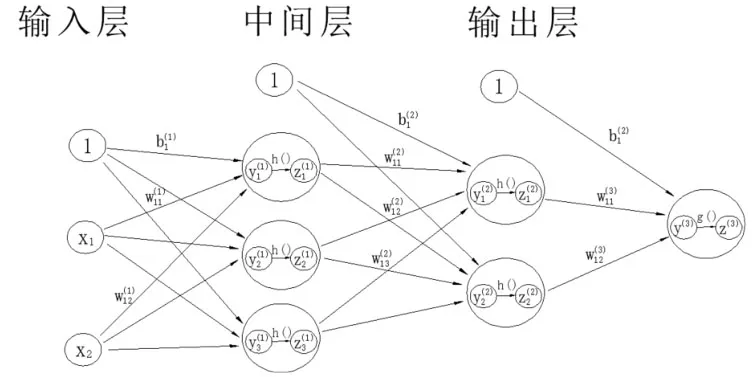
图1 神经网络结构Fig.1 Neural network structure

图1中神经网络正向传递第一层第一节点的实现过程为,y1（1）=w11(1)x1+w12(1)x2+b1(1)，h()为激活函数，激活函数为非线性函数，利用激活函数可实现非线性数据的回归分析。常用的激活函数为h(x)=1/(1+exp(-x))，类似可得第二层第一节点的实现过程：输出层激活函数为g()，回归分析时激活函数一般用恒等函数，也就是z（3）=y（3）。使用矩阵乘法运算神经网络正向传递可以表示成Y=WX，其中：

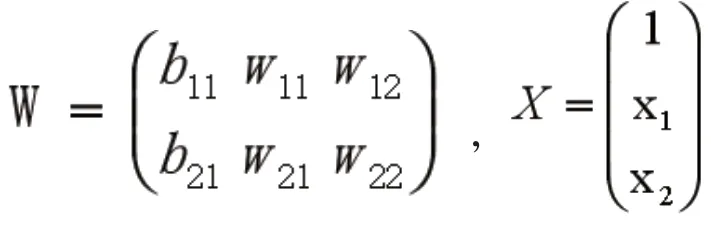
给神经网络合适的权重矩阵W，可实现数据分类或回归。权重矩阵事先是未知的，通过样本数据对神经网络进行训练获取权重矩阵。

要实现从数据中学习，获取权重矩阵，要用到损失函数，用其计算当前神经网络输出值与训练数据的差值。常用的损失函数有：

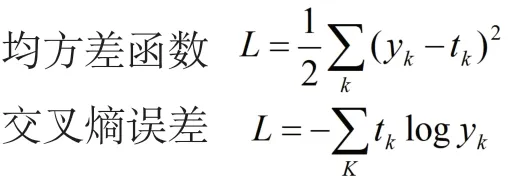
对损失函数的权重矩阵W求偏导数得到神经网络的梯度，其性质是指向损失函数减小的方向。通过迭代得到新的权重矩阵，迭代公式如下。

其中η为学习率，一般设定为0.001。根据梯度的性质，新权重矩阵构建神经网络的损失函数值小于上一次的值，将迭代次数设为一个较大的值如1000，通过循环实现损失函数不断减小的同时，最终获取最优的权重参数。神经网络训练过程会遇到两类问题:收敛速度慢，容易陷入局部最优（非全局最优解）。Levenberg-Marquardt训练算法是解决非线性最小二乘问题的一种方法[11]它使用更新权重矩阵。其中：

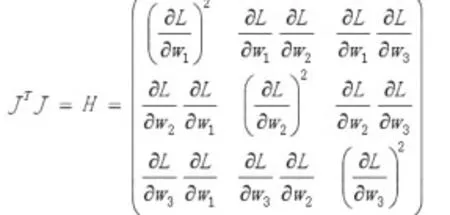
2 工程实例

本文选择同一小区的两幢高层建筑物的沉降观测数据进行处理，两幢建筑物均为18层，各布设8个沉降点，共进行了14期沉降观测，部分沉降点被破坏观测次数不满14次。将两幢建筑沉降观测值整合在一起共获得90次沉降观测数据。截取部分数据如表1所示。选取2019年12月3日至2020年8月19日的60次观测数据作为神经网络训练样本，2020年9月30日至2021年9月8日的20次观测数据用作检验样本。实测值与神经网络预测值比较情况如表2所示。

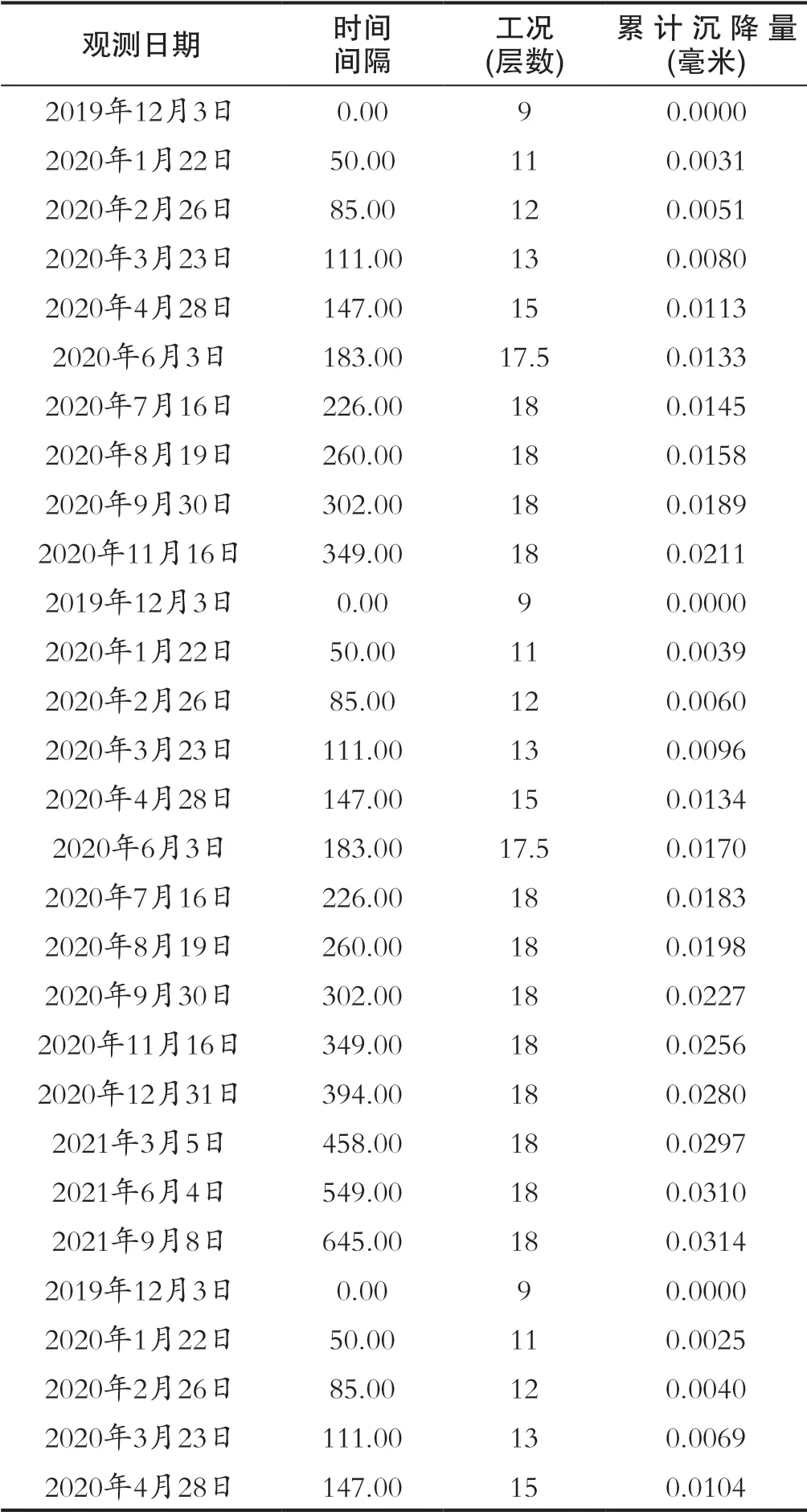
表1 原始观测数据Tab.1 Original observation data

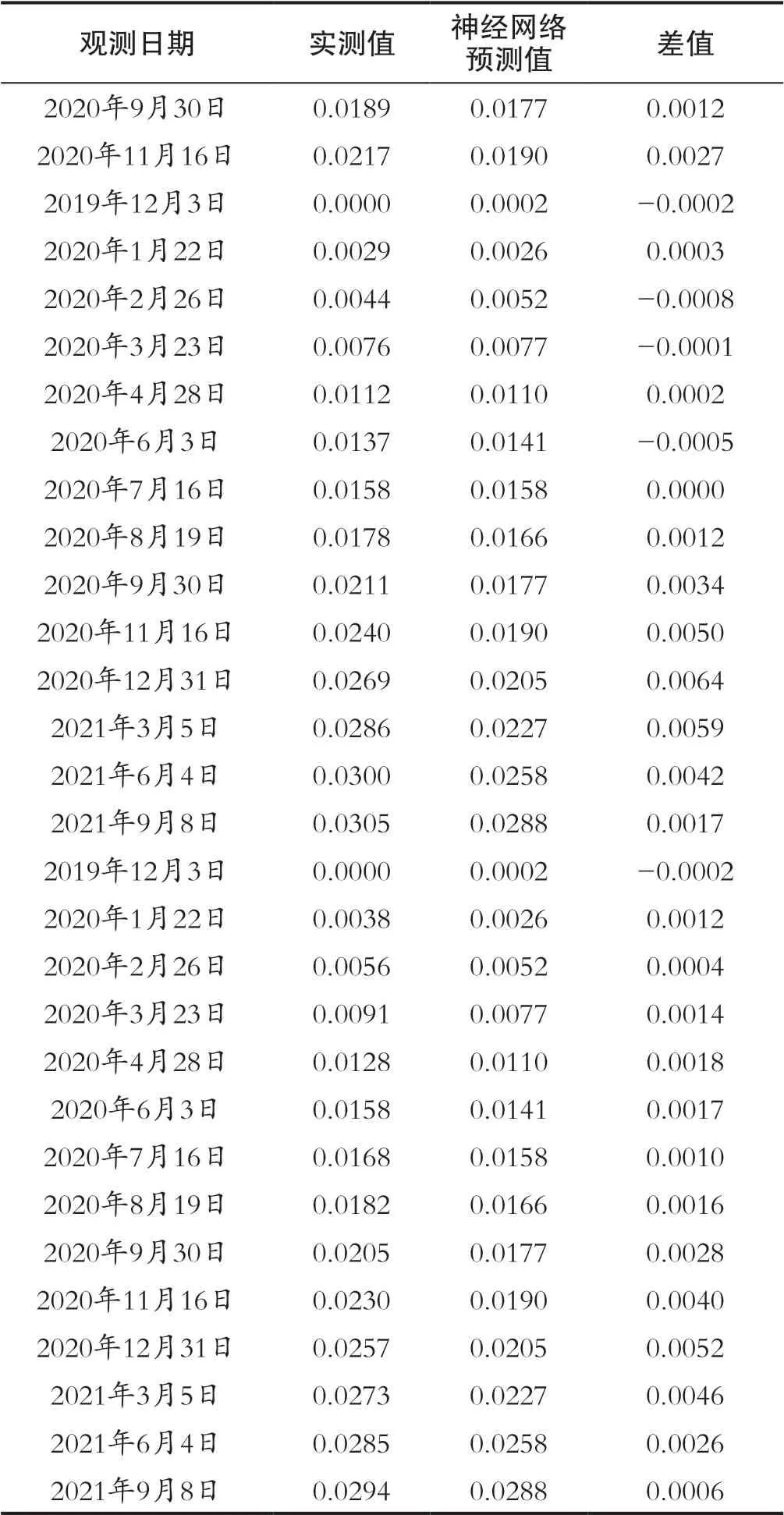
表2 实测值与预测值对比Tab.2 Comparison of measured and predicted values

3 多元线性回归检验

将沉降观测时间间隔和观测时的建筑荷载（施工层数）作为自变量，沉降值作为因变量，建立多元线性回归模型。通过R2检验和F检验判别多元线性回归模型的可靠性[1]。利用上文60个样本数据，通过最小二乘法，得到方程y=-0.0105+0.00002886x1+0.0011x2，同时得到方程的R2检验值为0.9176、F检验值为317.3768。R2=0.9176说明y值的变化中有91.76%由x1和x2引起的。查表得F0.005(2,60)=199.5，F>F0.005(2,60)说明在显著水平0.005下，y与x1和x2之间线性相关关系特别显著。将2020年9月30日至2021年9月8日的20次观测数据用作检验数据带入多元回归方程，获取多元回归预测值。图2为神经网络预测值和多元线性回归误差曲线。

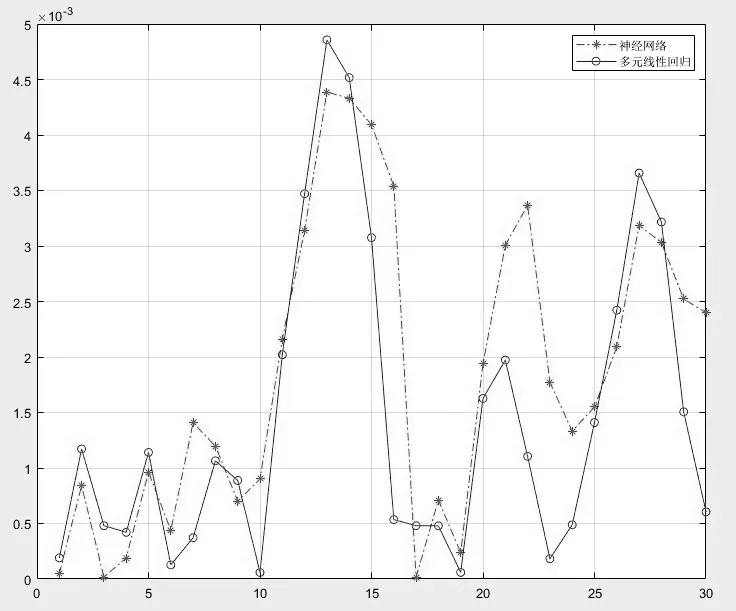
图2 神经网络与多元回归误差曲线Fig.2 Neural network and multiple regression error curve

4 结论

本文将高层建筑荷载（施工层数）和沉降监测时间间隔作为自变量，沉降值作为因变量，利用Levenberg-Marquardt神经网络方法进行高层建筑物沉降值预测，并利用多元线性回归分析方法进行验证，表明利用Levenberg-Marquardt神经网络方法进行高层建筑沉降数据预测分析是可行的。