陇海线咸阳渭河大桥纵向力分布规律及其结构影响因素分析
2022-02-18屈直
屈 直
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
近些年,由于我国铁路发展的需要,一些特殊结构桥梁因具有大跨越能力、美感和经济性等优点,开始出现在铁路桥梁建设中[1-3]。由于钢桁架桥具有施工快捷方便,刚度大、跨越能力较大的特点,十分适合大跨度铁路桥梁[4-6]。如位于纽约的赫尔盖特桥和位于澳大利亚的悉尼港大桥等。我国在建设拱桥中具有悠久的历史,1300多年前就建成举世闻名的赵州桥。20世纪70年代后,钢拱桥开始出现在我国铁路建设中,有主跨(180+216+180)m的九江长江大桥[7],主跨552 m被誉为“世界第一拱桥”的朝天门长江大桥[8],主跨336 m的南京大胜关长江大桥及主跨490 m的怒江四线特大桥[9-10]。
以往对于桥梁纵向力的研究主要集中在简支梁、连续梁等普通桥梁上,针对钢桁架拱桥涉及较少,尤其拱桥结构相对比较特殊,其具有拱肋、吊杆等特殊结构。因此,有必要对钢桁架拱桥上无缝线路的受力及变形规律进行研究。在铁路桥梁设计时,梁轨相互作用是研究无缝线路的关键问题,以此来分析温度荷载、列车荷载、制动荷载及断轨工况下伸缩力、挠曲力、制动力及断轨力的钢轨纵向力受力变形情况。一些学者对这一问题进行了研究:如 Fryba[11]将轨道假定为等截面的弹性杆件,采用梁轨整体法计算分析模型;佐藤裕[12]推导了在桥上铺设长钢轨时,桥梁和桥上钢轨间的相互作用力;Coenraad Esveld[13]在其著作中阐述了钢轨附加力的机理,并对纵向阻力进行了研究,开创了用有限元法计算附加力的先河;徐庆元[14]采用非线性弹簧单元模拟纵向阻力;建立了三维有限元模型,研究了常阻力及小阻力扣件、桥跨数量等对梁轨相互作用的影响;戴公连[15]假设轨道横向和竖向与桥梁不发生相对位移,用竖向刚臂模拟梁高,用非线性弹簧模拟梁轨之间纵向连接刚度,比较了纵向阻力、梁体约束方式及温差等对梁轨相互作用的影响;刘文硕[16]基于非线性空间分析,建立了考虑荷载加载历史的梁轨有限元模型,分析了纵向力的分布规律。为研究此类桥梁梁轨受力及变形规律,本文以陇海线咸阳渭河大桥为例,计算连续钢桁架拱桥上无缝线路纵向力及梁轨相对位移,分析影响纵向力的因素。
1 工程概况
1.1 桥梁概况
以陇海铁路咸阳渭河大桥为例,该桥全长约800 m,为十一联连续钢桁架拱桥,处于陇海线与咸铜线的交汇处。本文在进行计算时简化为三联连续钢桁架下承式拱桥,结构布置如图1所示。
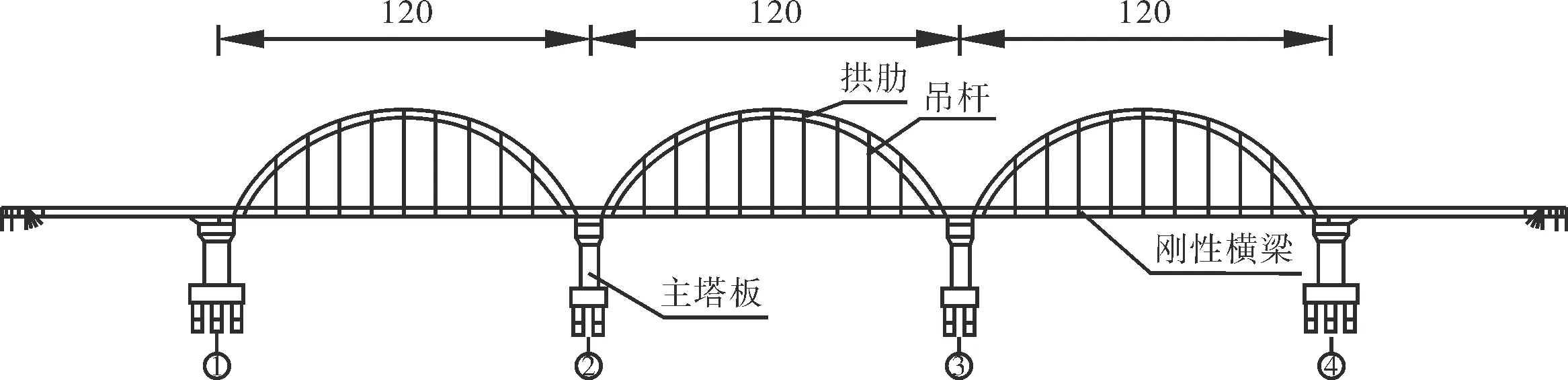
图1 拱桥结构布置(单位:m)
计算跨径360 m,考虑梁端两侧路基上线路纵向阻力对钢轨的约束,在拱桥两侧建立100 m路基。主桥拱肋采用钢桁架拱结构,全桥位于直线段上,属于有砟轨道无缝线路。
拱肋及立柱墩台布置如图2~3所示。
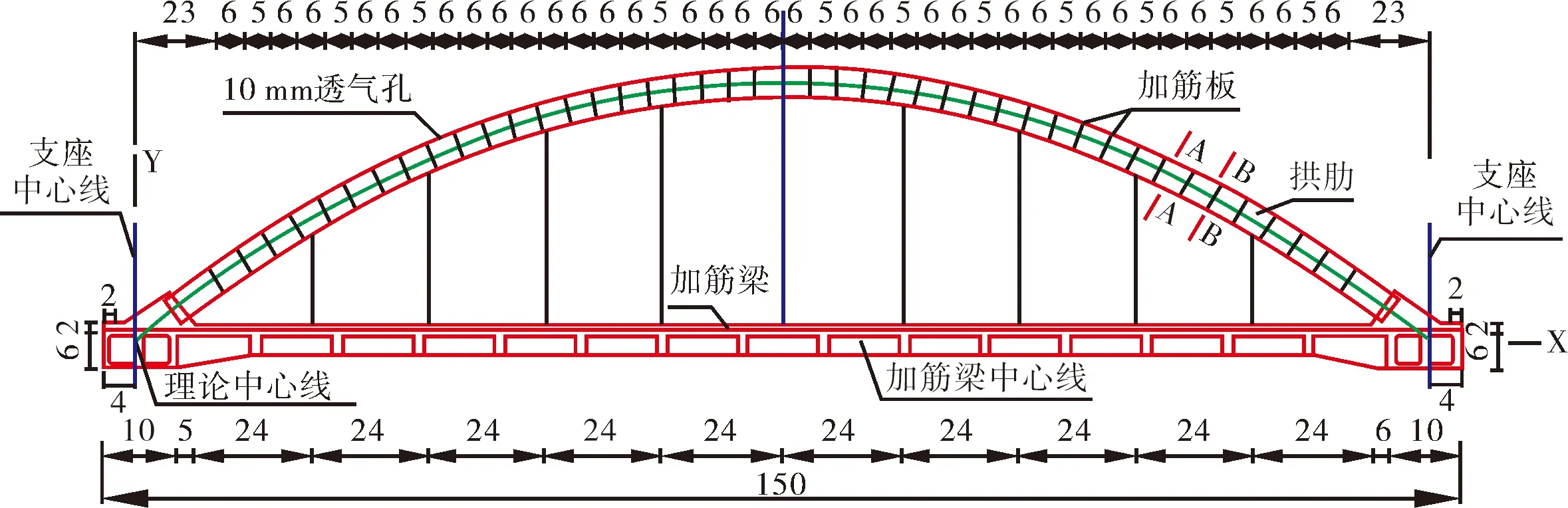
图2 1/3拱桥拱肋结构立面
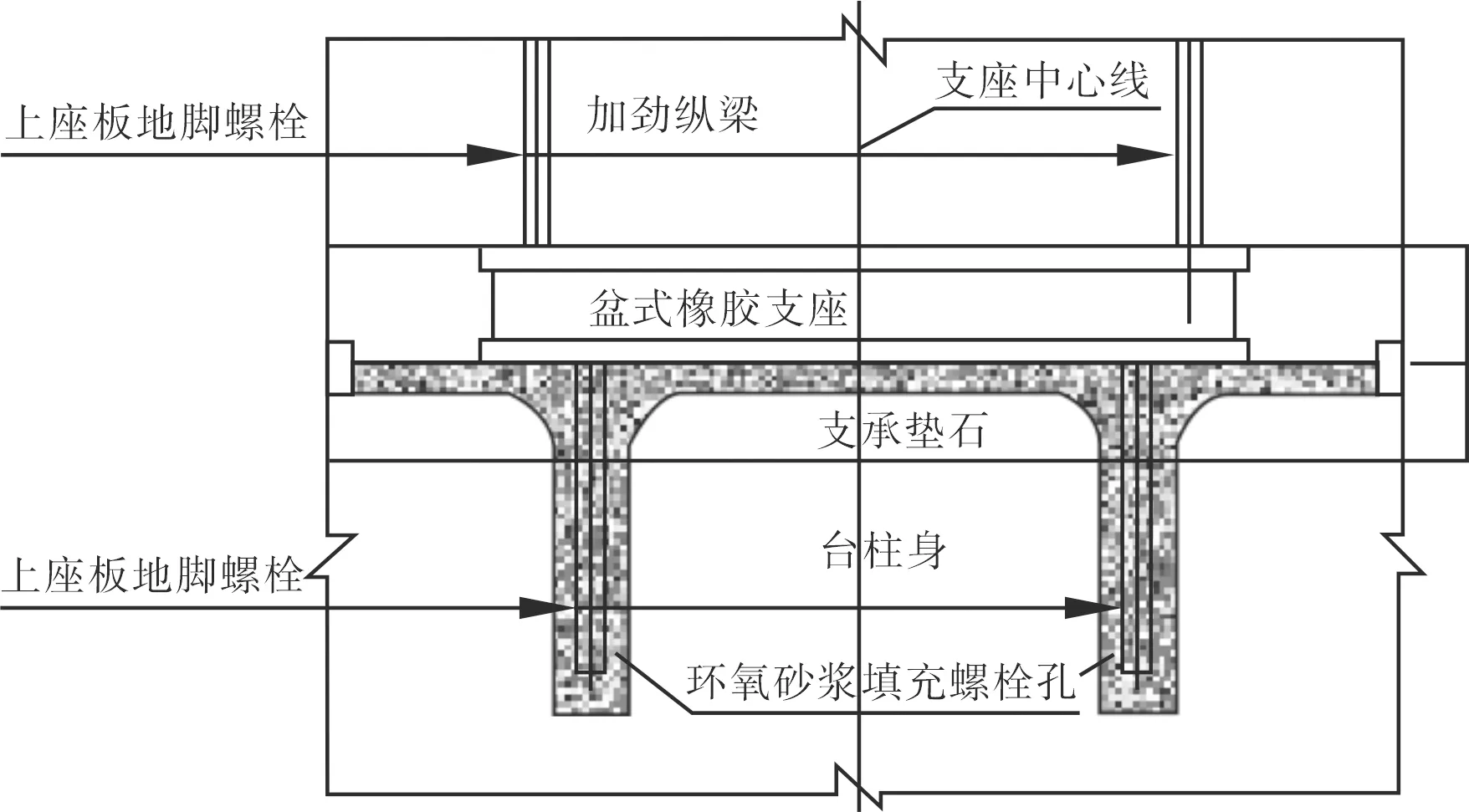
图3 立柱墩台结构立面
1.2 计算参数选取
钢轨是铁路线路中最重要的结构,该工程采用 60 kg/m钢轨。根据我国规范,结合本文对桥梁结构性分析,梁温差取15 ℃。设计中采用中-活载加载时,标准活载计算图示可任意截取。计算制动力时,轮轨粘着系数μ=0.164。
2 计算模型
2.1 拱桥线桥墩一体化模型
拱桥线桥墩一体化计算模型如图4所示。主桥跨径布置为120 m+120 m+120 m,此桥梁结构体系的特点是:钢轨通过线路的纵向阻力沿纵向与主梁上缘相互作用。主梁通过立柱墩及吊杆将纵向力和竖向力传递给拱肋。钢轨、主梁、刚性横梁及拱肋是一个耦合的相互作用系统,在不同的计算条件下,每一部分的应力和变形都有一个独特的平衡点,找到平衡点可以得到各部分的应力和位移。

图4 线桥墩一体化计算模型
计算模型中,主拱两端的计算段设置为100 m路基段,按连续钢桁拱结构拱桥上无缝线路计算。吊杆连接的主梁为三跨梁体,吊杆与主梁的连接位置在主梁梁面,与设置在主梁上的刚性横梁固结;拱桥两端桥梁计算段墩台,其结构型式与主桥的连接反应在安装支座处墩台的纵向水平刚性上,采用不同截面尺寸参数输入来表示;模型中将拱肋进行了简化,结构形式上取为梁单元;拱肋和拱轴线采取两次抛物线形状。
2.2 拱桥有限元模型
钢轨纵向阻力与混凝土梁在纵向上相互作用,支撑墩与梁底缘连接传递纵向力。在有限元软件ANSYS中,采用杆单元、线单元和吊架单元,梁单元BEAM188可选用拱肋、梁体和刚性横梁;采用非线性弹簧模拟纵向阻力,线性弹簧模拟路面纵向和横向刚度。根据以上假设和分析,对于拱桥上无缝线路各种结构建立了耦合模型,如图5所示。

图5 拱桥上无缝线路耦合模型
3 纵向附加力计算
文中所有图、表输出内容均以左端简支梁及固定支座桥台起点为坐标系原点,正值表明钢轨受拉产生伸缩变形,负值则表明钢轨受压产生了压缩变化。
3.1 伸缩附加力计算
计算时选取钢梁温差25 ℃,分别计算2种工况下伸缩附加力变化曲线,结果如图6所示。工况1:不考虑拱肋温差;工况2:拱肋温差25 ℃。
由图6可知,工况1与2在拱桥梁体整体升温25 ℃情况下,拱桥左右端部与路基连接处钢轨均受压力,拱桥中间位置钢轨均受拉力,且受力比较均衡,没有发生明显突变。不考虑拱肋温差时,钢轨最大压力出现在右侧梁端,钢轨伸缩力最大值为431.1 kN;考虑拱肋温差25 ℃时,钢轨最大压力出现在右侧两端,钢轨伸缩力最大值为720.6 kN,该值是不考虑温差时的1.7倍,钢轨拉力在数值上大于钢轨压应力。由此可见,拱肋温差对钢轨的伸缩力有很大影响,主要是拱肋在温度作用下的内缩或外涨变形,导致桥墩桥台沿拱肋线方向的挠度发生变化。桥墩和桥台的挠度使梁沿直线方向位移,由于线路阻力的存在,钢轨将产生较大的伸缩力。一般来说,由于拱脚附近有桥台,即使挠度角很小,桥台顶部也会产生较大的位移。因此,在拱脚附近的桥墩和桥台处,钢轨的伸缩力将出现较大的峰值。因此,可以认为拱肋温差的变化,能直接影响到拱桥桥上无缝线路伸缩附加力,检算钢轨强度时应当加以考虑。
1) 拱肋温差。
拱肋温差分别为15、20、25 ℃时钢轨伸缩附加力变化曲线如图7所示。
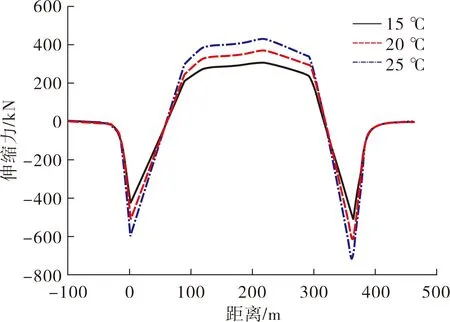
图7 钢轨伸缩力变化曲线
由图7可知,拱肋的温差对桥上无缝线路受力变形有一定影响,不同温度下钢轨伸缩力最大值依次为514.7、617.6、720.6 kN。随着拱肋温差增大,钢轨的伸缩力总体呈增大趋势。经过计算得到受拱肋温差影响的钢轨伸缩力,拱肋温差为25 ℃时是20 ℃的1.2倍,钢轨伸缩力的分布基本相同,没有突变。因此,在拱桥无缝线路设计时必须考虑合理的拱肋温差。
2) 立柱墩台温差。
立柱墩台温差为15、20、25 ℃时,钢桁梁与拱肋的温差在3种工况下均考虑为25 ℃,伸缩附加力变化曲线如图8所示。
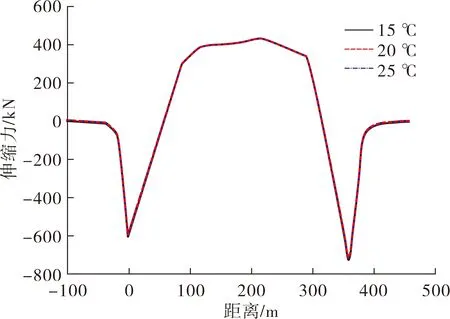
图8 钢轨伸缩力变化曲线
由图8可知,立柱墩温差的增大,对于钢轨的伸缩力影响较小,总体呈略微增大趋势。这是由于拱肋截面的转动会引起立柱墩台的挠度变化,立柱墩的温度变形会因梁体的纵向位移而略有减弱。由此可知,立柱墩台温差对纵向附加应力和纵向变形影响不大。
综合以上因素,可以得出拱肋温差对伸缩力有一定影响,而对于立柱墩台温差的变化,对钢轨的伸缩力的影响则较小。考虑到立柱墩台与拱肋为一整体结构,建议立柱墩台温差取同拱肋温差。
3.2 挠曲附加力计算
3种挠曲工况加载模式下钢轨受力效果如图9所示,钢轨挠曲附加力变化曲线如图10所示。
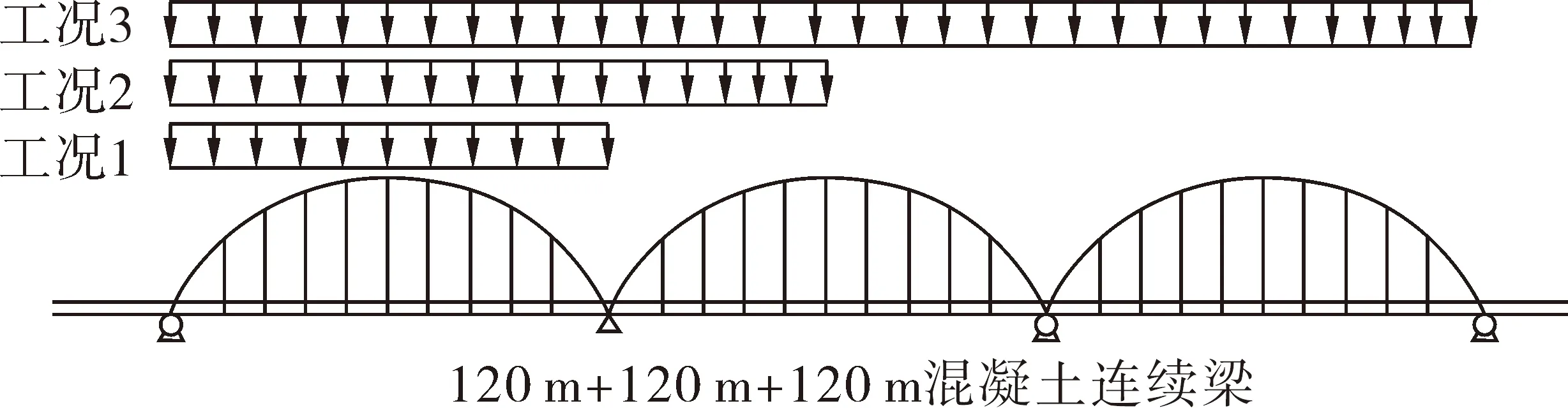
图9 不同挠曲加载工况
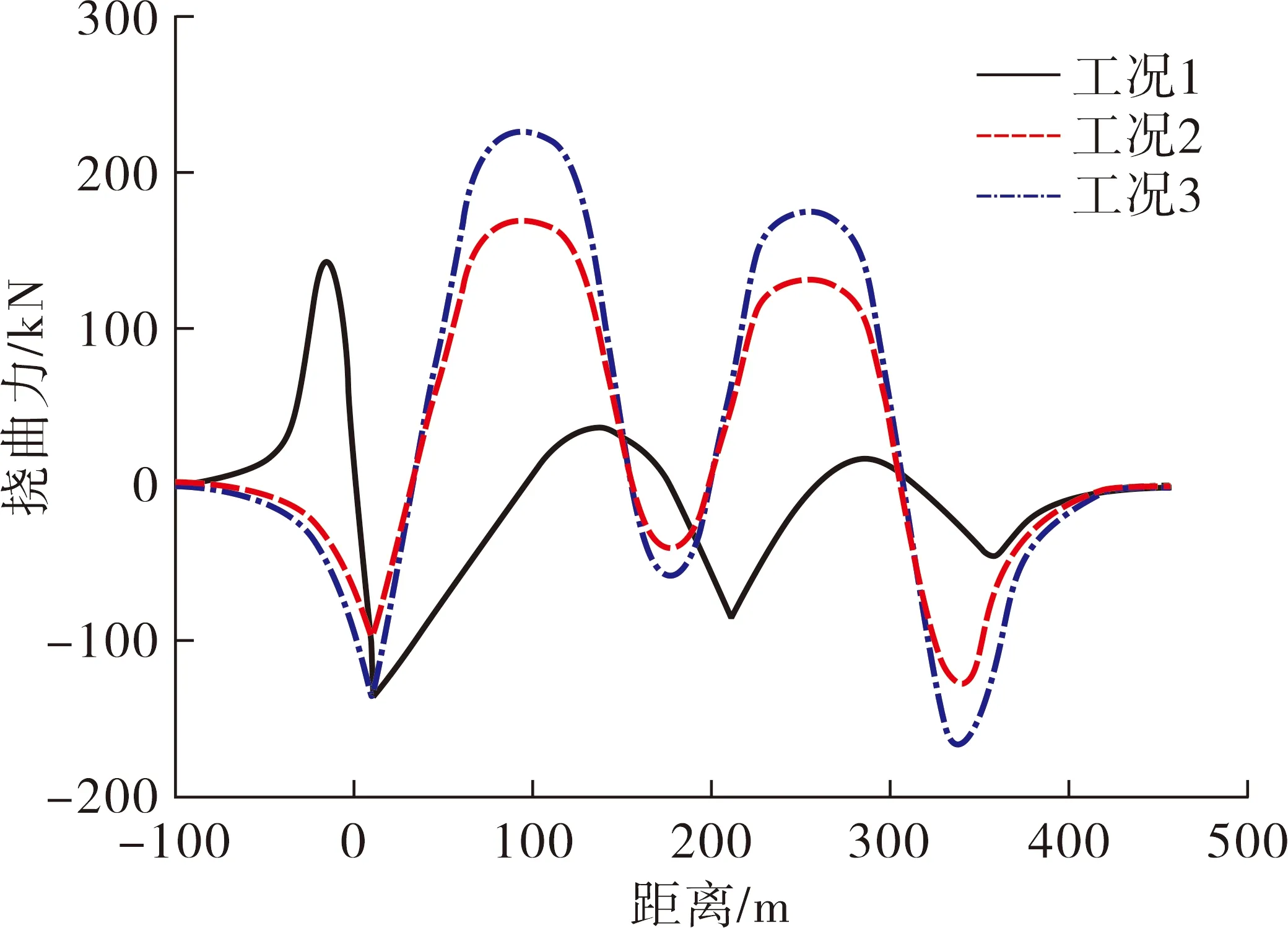
图10 钢轨挠曲附加力变化曲线
工况1:左侧主梁第一拱部分加载;
工况2:桥梁跨中与一拱部分之间加载;
工况3:全桥加载。
由图10可知,在计算挠曲力时,荷载布置形式对钢轨挠曲力的影响很大,3种工况下挠曲力最大值分别为140.1、173.2、226.0 kN。通常来讲,对于拱桥而言,当荷载布置在拱桥的满跨上(即第3种工况)时,钢轨的挠曲拉压力达到最大,图中最大挠曲力约为226.0 kN,相比于一般简支梁,其最大挠曲力不会超过100 kN。这主要是因为当荷载分布在整个拱桥上时,拱肋受力会不均匀,拱肋近似为反对称的变形较大,因此钢轨的挠曲力就会很大。算例中只是计算了荷载单方向入桥的工况,在进行拱桥无缝线路挠曲力计算时,建议在拱桥满跨时布置荷载,并考虑荷载入桥方向的变化,按照最不利的计算结果考虑。
1) 拱肋刚度。
拱肋刚度分别为0.5、1.0和2.0倍时,钢轨挠曲附加力变化曲线如图11所示。
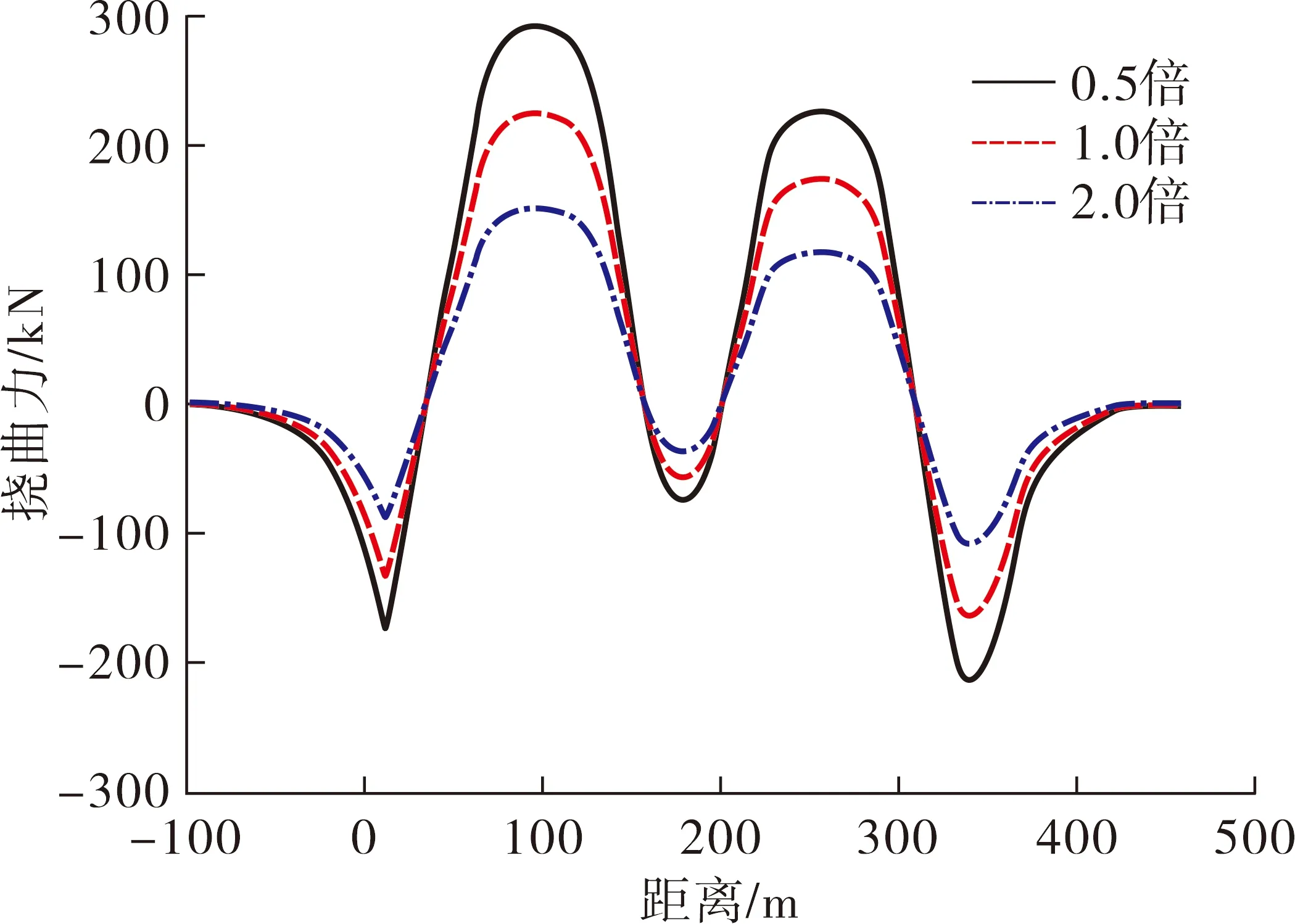
图11 钢轨挠曲力变化曲线
由图11可知, 拱肋刚度对钢轨挠曲力及线路变形的影响较大,3种拱肋刚度下钢轨挠曲力最大值分别为293.8、226.0、150.7 kN。0.5倍拱肋刚度时钢轨挠曲力计算结果几乎是2.0倍拱肋刚度的2倍。这是因为当拱肋刚度相对较小时,列车荷载通过立柱墩台传递到拱肋上,导致拱肋产生较大变形。拱肋变形后的转动会引起立柱墩台的挠度变化,导致梁的纵向位移较大。此外,可以预测,随着拱肋刚度的增加,拱肋在荷载作用下的变形将减缓,从而减缓钢轨挠曲力的下降趋势。
由此可知,拱肋刚度的变化对纵向力有一定影响,主要是对钢轨的挠曲力有较大的影响,而对伸缩力影响不大。而在钢轨强度检算中,一般采用钢轨最大伸缩力或挠曲力的最大值进行计算。从计算结果来看,钢轨的挠曲力不能作为钢轨强度检算的控制条件。
2) 立柱墩台刚度。
立柱墩台刚度分别为0.5、1.0和2.0倍时,挠曲附加力变化曲线如图12所示。
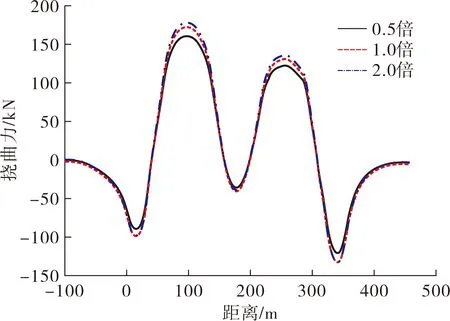
图12 钢轨挠曲力变化曲线
由图12可知,立柱墩台刚度对挠曲力下线路受力变形的影响没有拱肋刚度的影响大,立柱墩台刚度大的钢轨挠曲力要大些,但整体来看变化不显著,这主要是因为引起钢轨产生挠曲力的主要因素是拱肋变形引起立柱墩台偏转进而带动梁体产生的位移,而3种工况下的拱肋刚度是一样的,拱肋变形差别会很小,立柱墩台刚度大的带动梁体产生的纵向位移要大些。因此,随着桥墩柱刚度的增大,钢轨的挠曲力略有增大,但两者之间的差异会越来越小。
3.3 制动附加力计算
2种工况下钢轨制动附加力荷载布置如图13所示,钢轨制动附加力变化曲线如图14所示。
工况1:1/2满桥加载;
工况2:全桥加载。
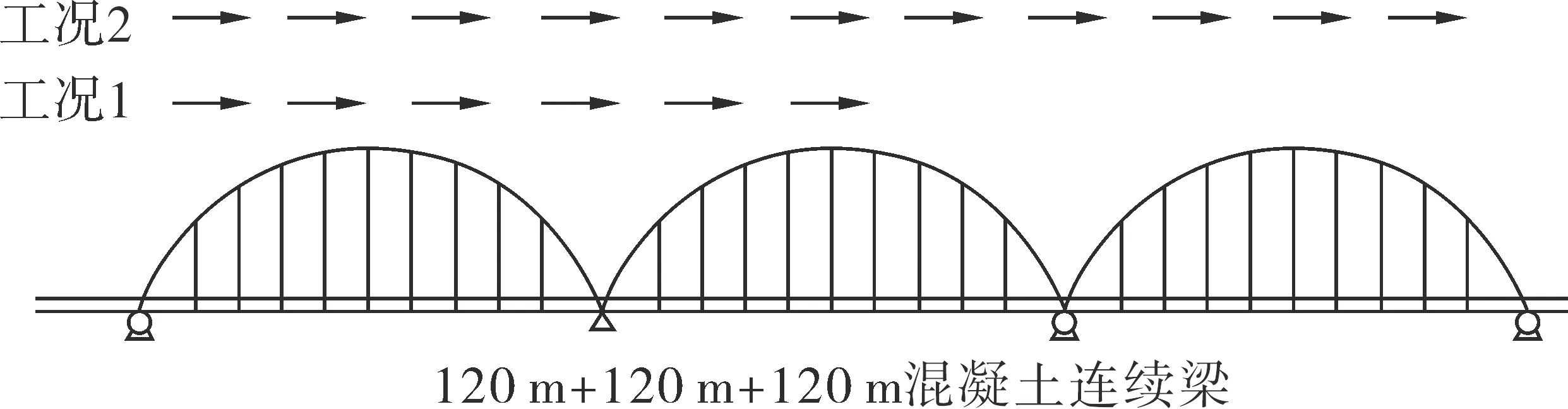
图13 不同工况下荷载布置
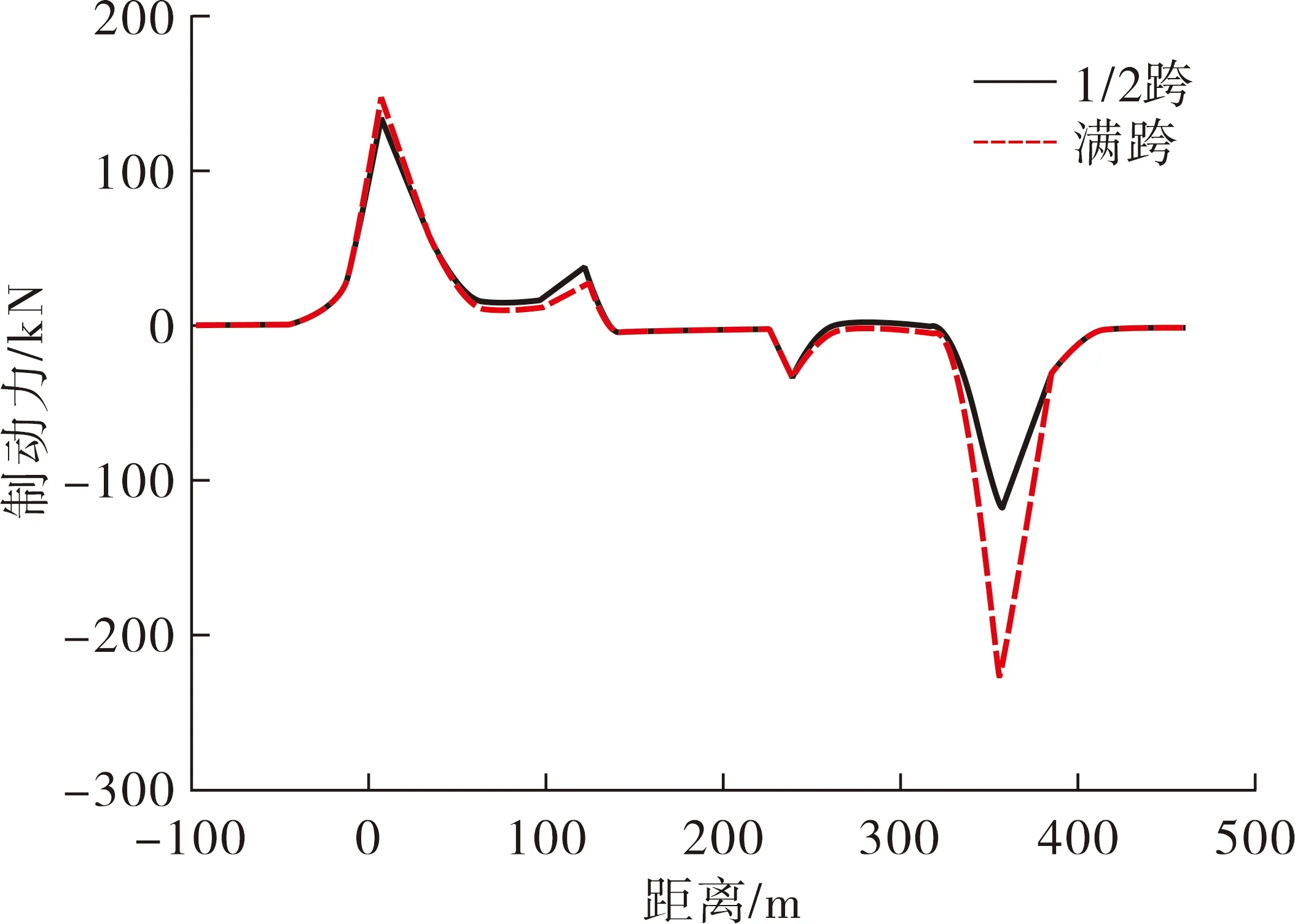
图14 钢轨制动附加力变化曲线
由图14可知,在2种工况下制动力的峰值都发生在主梁两端,而钢轨纵向力在其它位置变化不大。为了得到更加合理的结果,与伸缩力相比制动力计算结果也较小。计算制动力时,在拱桥全跨制动时,钢轨制动力达到最大值,整个拱肋的变形与挠曲力计算时在拱桥的半跨加载的拱肋变形相似。算例中只是计算了荷载单方向入桥的工况,在进行拱桥无缝线路制动力计算时,建议在拱桥满跨时布置荷载,并考虑荷载入桥方向的变化,按照最不利的计算结果考虑。
1) 拱肋刚度。
拱肋刚度分别为0.5、1.0、2.0倍时,钢轨制动附加力变化曲线如图15所示。
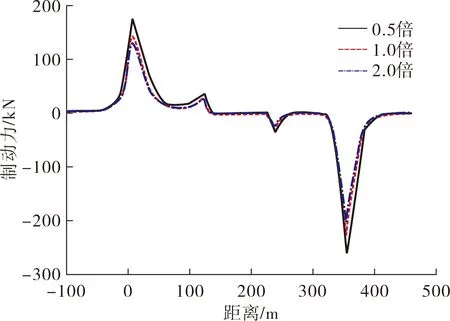
图15 钢轨制动附加力变化曲线
由图15可知,当拱肋刚度相对较小时,钢轨制动力值较大。随着拱肋刚度的增加,这些结果将变小,但差异不显著。为了更加合理的研究拱肋的影响,通过比较拱肋刚度对挠曲力的影响,发现拱肋刚度对制动力的影响小于对挠曲力的影响,而挠曲力的大小主要与拱肋变形引起的立柱墩台位移有关。因此,拱肋刚度对挠曲力的计算影响要大些,而对制动力的影响相对较小。
2) 立柱墩台刚度。
立柱墩台刚度分别为0.5、1.0、2.0倍时,钢轨制动附加力变化曲线如图16所示。
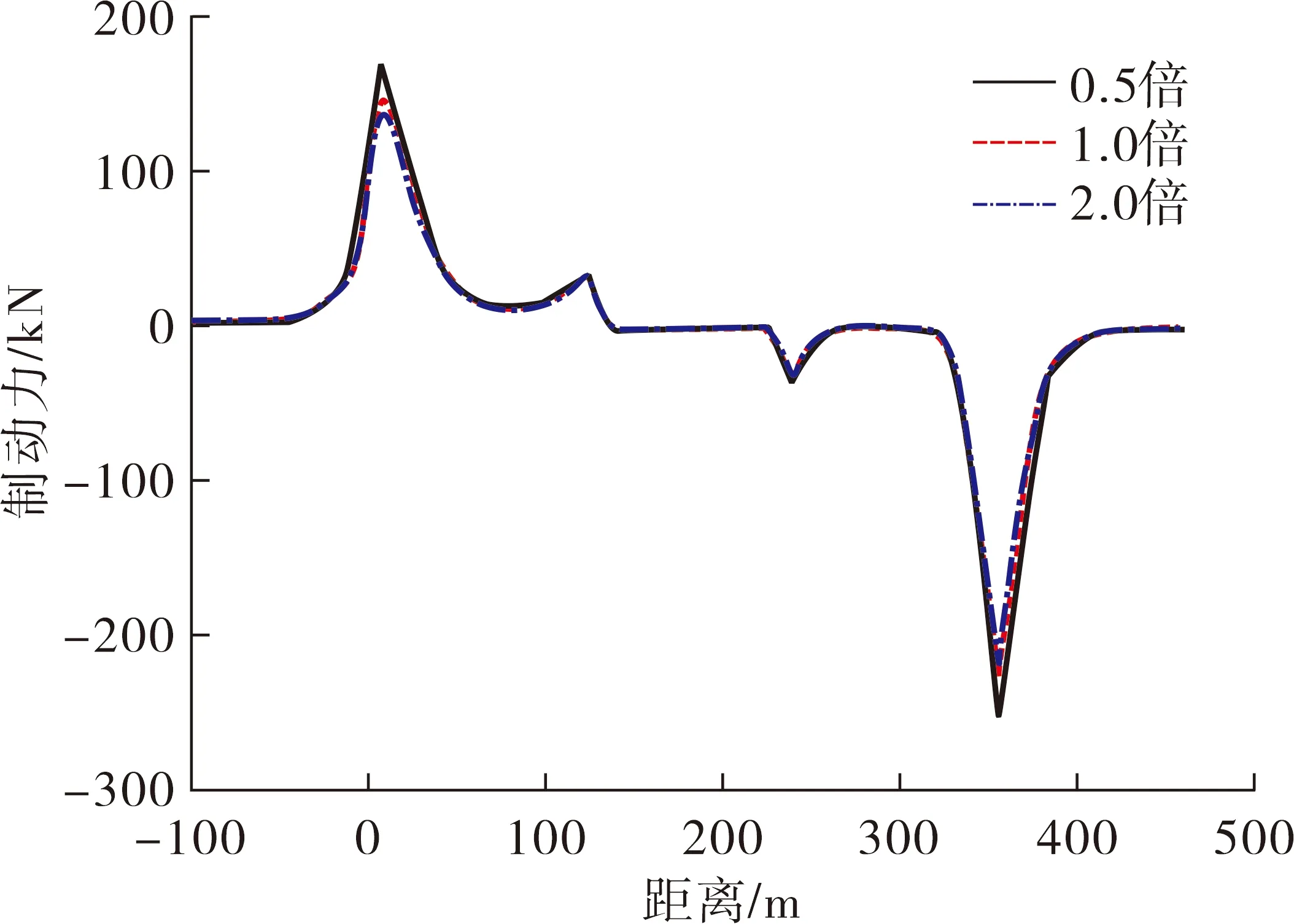
图16 钢轨制动附加力变化曲线
由图16可知,立柱墩台刚度改变影响到纵向力的变化,钢轨的制动力有一定程度减小,纵向力变形的分布规律与普通桥梁上的无缝线路相同。制动力有两个较大的峰值,两侧制动力的两个峰值位于主梁两端与路基连接处,这个地方也是车辆的前部和后部,其不受立柱墩台刚度变化的影响。拱桥跨径中间某一区域的变化很小,因为虽然立柱墩台刚度整体变化,但由于拱桥跨径中间的一些柱和桥台高度较低,仍然具有很大的刚度,来自钢轨的制动力不足,导致大变形和位移变化。
根据以上对制动力影响因素的分析可知,单独改变拱肋刚度或立柱墩台刚度对制动力的计算结果影响并不是很明显。
4 钢轨强度检算
查阅咸阳地区轨道设计相关资料发现,最高轨温54.5 ℃,最低轨温﹣12.1 ℃,设计锁定轨温为30 ℃;主梁边跨箱梁日温差取为15 ℃,计算考虑拱肋温差25 ℃、立柱墩温差20 ℃,最大升温△t为24.5 ℃,最大降温△t为42.1 ℃,根据温度力计算公式σt=2.478△t,可得最大升温温度应力σt=2.478×24.5=60.7 MPa,最大降温温度应力σt=2.478×42.1=104.3 MPa,最大动弯压应力为107.3 MPa,最大动弯拉应力为123.5 MPa。根据规范,钢轨最大拉应力为轨道强度检算最不利因素,故主要检算钢轨拉应力强度是否满足要求,以避免钢轨被拉断。钢轨强度检算结果如表1所示。

表1 钢轨强度计算结果
根据钢轨强度检算结果可知检测值小于容许应力,无缝线路钢轨强度均满足规范要求。
5 结论
1) 类似拱桥无缝线路设计时必须考虑合理的拱肋温差;立柱墩温差对线路受力变形影响较弱,考虑到立柱墩台与拱肋为一整体结构,建议立柱墩台温差取拱肋温差。
2) 满载时钢轨挠曲力最大,最大挠曲力出现在主桥右端端部。拱肋刚度对钢轨挠曲力有很大影响,钢轨挠曲力远大于普通桥梁上无缝线路的挠曲力,建议重视该类桥梁的挠度状态分析。立柱墩台刚度变化时,立柱墩台刚度较大的钢轨挠曲力较大,但总体变化不显著。
3) 拱桥右侧梁端处钢轨制动力达到最大值。制动力峰值出现在两端位置,其余位置纵向力都不大。经过研究发现,改变拱肋刚度或立柱墩台刚度其中任意一个因素时,对制动力的计算结果影响并不显著。
4) 拱桥线路中钢轨发生断轨时,钢轨纵向力在断轨处数值接近0,在此出现折断钢轨纵向位移的最大值。
