基于PLSMA-SVR模型的井采工作面瓦斯涌出量分析预测
2022-02-18汪浅予张义龙
汪浅予,张义龙
(1.深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001;2.安徽理工大学 a.机械工程学院;b.人工智能学院,安徽 淮南 232001)
煤矿在开采过程中会伴随着多种灾害事故的发生,例如瓦斯爆炸、煤尘爆炸、煤与瓦斯突出等。据统计,瓦斯爆炸约占特大事故总数的70%左右,瓦斯可称为煤矿安全的最大威胁者,因此,本文就煤矿开采过程中工作面的瓦斯涌出量为研究方向,分析影响瓦斯涌出量的多重因素,同时基于影响因素做到对瓦斯涌出量的提前精准预测,从而达到减少事故发生,降低人员伤亡,为煤矿安全做出贡献。
针对瓦斯涌出量的预测研究,多位专家学者已经对此展开了探索,较为传统的方式主要有矿山统计法和分源预测法;现有的预测方法有动、静预测两大类型[1],静态预测即通过考虑地质条件加上人为开采因素进行涌出量的预测;动态预测指利用监测系统,综合时间序列进行规律挖掘。随着人工智能技术在各行业的应用,不少学者在瓦斯涌出量预测方面采取了新型的智能算法,胡坤[2]等针对回采工作面瓦斯量预测建立了TLBO-LOIRE模型;王媛彬[3]等提出基于主成分分析法和极端梯度提升结合的矿井回采工作面瓦斯涌出量预测方法;谭云亮[4]等将灰色理论技术和自适应策略下的小波神经网络运用在涌出量预测方面。当下,支持向量机因其独特的小样本处理优点被广泛运用在各种类型预测上,包括本文所提瓦斯涌出量预测。李超群[5]等利用支持向量机和模型树相结合的方法对瓦斯涌出量进行预测;王磊[6]等就瓦斯涌出量预测建立了IABC-LSSVM模型。鉴于上述研究,本文利用改进后的黏菌算法对支持向量回归进行参数优化,建立一种新型的PLSMA-SVR瓦斯涌出量预测模型,后续利用现有历史一线数据对所提模型进行训练验证,同时采取对比分析的方式验证该模型的可行性。
1 基础算法理论
1.1 支持向量回归
支持向量回归[7](SVR)本质与支持向量机(SVM)相同,其作为支持向量机基础下的一个应用分支,两者区别在于个体到超平面的“距离”,SVR要求最远个体“距离”最小,SVM则要求最近个体“距离”最大。本文选择SVR作为预测算法,主要基于SVR采用核函数解决了过程拟合的优势,可以实现非线性回归,同时达到“升维”目的,有利于解决小样本、非线性函数问题,建立数学模型。
给定训练数据集Z,定义回归函数为
f(a)=ωTa+t,
(1)
式中:w和t分别指代权值向量和偏置向量;a为个体样本。通过融合带入松弛因子,得到优化函数模型,即
(2)

选择径向基函数作为核函数,得到
K(a,ai)=exp(-gamma‖x-xi‖2),
(3)

(4)
1.2 黏菌算法基础理论
黏菌算法[8]以黏菌生物的动态觅食阶段为启发,使黏菌中有机物的“寻食、围食和消食”三个活跃阶段在算法中得以体现。黏菌进食过程存在一种细胞质流量与黏菌静脉厚度之间的正-负反馈组合,该组合意义在于使黏菌可以建立相对优越的最佳路径,以此来构建连接食物的通道,在外界食物来源质量不相同的情况下,反馈机制促使黏菌朝向高浓度区域进发。黏菌算法依据自适应权重的调整来模拟上述过程,经多位研究学者验证,该算法在搜索能力、搜索环境以及竞争方面具有较突出优势,三个搜索阶段具体情况如下:
1) 寻食。
食物来源浓度不同,正-负反馈组合机制下的黏菌通过感知变化,不断调整自身与食物间的距离,其调整行为公式如下:

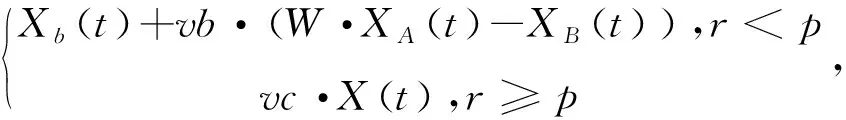
(5)
式中:X指此刻黏菌所处的位置;vb指范围在[-a,a]的参数;vc指范围在[0,1]的参数,特征为从1到0线性降低;t指此刻的迭代次数;Xb指此刻黏菌依据感知浓度变化所搜寻到的最佳食物位置;XA和XB指此阶段的两个随机黏菌个体;W指黏菌重量。参量p、a以及W如式(6)~(9)所示:
p=tanh|S(i)-DF|(i∈1,2,…N),
(6)

(7)
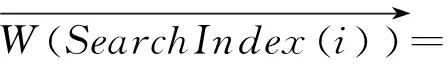

(8)
SearchIndex=sort(S),
(9)
式中:S(i)指个体适应度,i∈1,2,…,n;DF指整体迭代中适应度的最佳值;T指迭代次数的最大值;N指黏菌种群的全体;condition指S(i)的值位于前1/2的个体;bF和wF分别指此刻迭代中个体适应度的最佳、最差值;SearchIndex指排序的适应度值序列(如果在最小值问题上,则按上升趋势呈现);现依靠Xb的变化可更新搜索个体的位置,依据vb、vc和W的调整可改变个体位置;r指范围在[0,1]的随意数,其意义在于提高搜寻到最优解的可能性。
2) 围食。
该阶段用数学模型呈现黏菌静脉组织的收缩情况,食物浓度越高,相对应静脉越厚,反之则相反。式(8)呈现了正-负反馈组合在黏菌形态和食物浓度之间的工作调整过程,log可对频率数值起到稳定调节作用;condition反映个体位置随行进的调整过程:高浓度区域,其个体重量越大,反之改变目标,调整搜索方向,对应个体重量变小。基于此原理,可确定黏菌的位置更新公式如式(10),即
X(t+1)=

(10)
式中:rand和r指在范围为[0,1]中随机选取的某一数值;ub指搜索过程中整体范围的上极限;lb为下极限;z意义在于贯穿全搜索过程的参数权衡。
3) 振荡消食。
此阶段呈现了黏菌进食过程,W、vb、vc三个参量的调整,模拟了整个进食过程中因食物浓度的不同,从而导致黏菌静脉形态和振荡频率所产生的变化,W秉持高加速、低减速原则,在食物浓度高时加快其移动至目标的速度,反之降低靠近速度,从而使搜寻到最佳食物浓度的效率达到最大化。不等同于其它觅食行为的单一性,黏菌为了使食物来源达到最大化,在已达到最佳位置进行消化的同时,其还会通过调整vb和vc的协同作用,分泌自身的一部分有机物去搜寻其它食物,其目的是避免单一食物来源,扩大化觅食,增加搜寻到更高质量食物的可能性。
2 改进黏菌算法
2.1 Piecewise混沌映射[9]
算法初始运行的关键体现在种群的初始化,其对算法的收敛性意义重大,并且会对算法的速度和精度产生比较大的影响,在多样性上占据优势的种群有利于提高算法效率和效果,同时,一个高质量的初始化种群可以弥补算法本身存在的某些类似搜索能力较差等瑕疵。目前所存在的种群初始化方法会造成种群个体很难统一获得高水平的质量,无法保证搜索区域全覆盖,因此只能增加迭代次数,同时会降低算法的运算速率,增加算法的计算复杂度。
黏菌算法和其它算法一样,在搜寻求解问题上通常以随机产生的初始个体作为初始化种群,且在运行初始时无先验知识,会产生在种群多样性方面的缺陷,因此需要确保初始种群的个体在随机前提下尽量分布均匀。
混沌映射是一种非线性性质下的序列生成方法,有利于控制种群初始化,提高种群多样性。因Piecewise映射形式简单,计算简便,其遍历性和随机性应用较为明显,本文选取Piecewise映射作为种群初始化优化策略,其具体映射描述如下:
f(k+1)=

(11)
式中:R的范围在(0,0.5),本文选取R=0.4;f(k)=rand。参量处于此范围内,可使初始处于混沌状态,融合Piecewise映射后的黏菌算法,实现在初始无序性等不足情况下,使种群分布更加均匀,遍历性有所提升,多样性问题得以优化解决。
2.2 Levy飞行策略[10]
黏菌的食物选择行为依靠的是不同个体间的协同作用,容易在最高浓度点停滞或者降低搜寻速度,使解陷入局部最优值,影响算法的精度;同时迭代全过程的振荡频率不能准确保证其稳定性,因此无法确保算法收敛速度的高效性,基于上述不足,引入Levy飞行策略进行优化。
Levy飞行策略最早由学者P Levy提出,策略来源受自然界动物寻食方式的启发,该策略特点体现在搜寻环境处在未知状态。Levy飞行策略实质是针对步长的概率分布和重尾分布进行随机性行走,基于此模式,可以达到行走过程处于短距离搜索和偶尔跨步长距离行走的特点,两种搜索方式结合可以实现寻食范围的全局域覆盖,有利于个体细致搜寻食物,保证食物的最大化利用,从而提升种群个体的寻优能力,使算法避免陷入局部最优,达到优化目的。该策略行走公式如式(12)~(14):

(12)
式中:L代表策略飞行运动的步长;β为常数,作用为调整函数形状,这里拟取数值1.5。参数μ和ν服从如下分布:

(13)
基于上述Levy飞行策略过程,现将其引入黏菌觅食过程,则最佳位置更新公式为
Xb*=Xb+1⊕L·Xb,
(14)

3 PLSMA-SVR模型整体描述
PLSMA-SVR模型是以SVR支持向量回归为基础算法,将融合Piecewise混沌映射和Levy飞行策略的PLSMA对SVR进行优化,调整参量的优选,具体步骤如下,流程如图1所示。

图1 PLSMA-SVR模型流程
4 实例研究与分析
国家安全生产监督管理总局2006年颁发的《矿井瓦斯涌出量预测方法》中指出,瓦斯涌出量的影响因素主要有开采层原始瓦斯含量、邻近层瓦斯含量、工作面日产量、开采深度等。本文综合考虑文件规定及相关煤炭专家研究结果,确定用以下10个影响因素作为瓦斯涌出量预测的训练指标,具体为:煤层深度(No.1)/m、开采位置原始瓦斯量(No.2)/(m3/t)、倾角(No.3)/°、煤层间距(No.4)/m、厚度(No.5)/m、邻近层瓦斯含量(No.6)/(m3/t)、煤层间的岩性(No.7)、开采推进速度(No.8)/(m/d)、瓦斯压力(No.9)/MPa和瓦斯抽采纯量(No.10)/(m3/min)。数据样本来源为陕西延安黄陵矿区4203综放工作面[11],以30组数据组成数据库,原始数据如表1所示,以前22个数据样本作为训练集进行训练,后8个数据样本作为测试集,测试结果以每分钟所产生的绝对瓦斯涌出量衡量。

表1 瓦斯涌出量原始数据
采用MATLAB2018b软件对表1数据进行训练,训练结果和预测结果如图2所示。

(a) 训练图
对比分析是最直观的效果呈现方式,为了增加本文所提模型的说服性,验证其可行性,拟采用其他2种不同模型对上述数据进行训练验证,具体为基础SVR训练模型、融合扰动策略和反向学习的DRSMA-SVR训练模型,2种训练模型预测结果如图3所示。

(a) 基础SVR模型
3种模型预测结果的具体值与误差如表2所示。

表2 模型预测对比结果
由表2可看出3种模型中PLSMA-SVR模型误差率处于较低水平,误差率低于1%的组数超过测试组数的1/3;DRSMA-SVR模型误差率相对较高,几乎都接近10%甚至超过20%;基础SVR模型预测误差率最高,有1/3组误差率高出10%,对比结果表明PLSMA-SVR预测模型的准确率居同类模型之首。
5 结语
本文基于煤矿回采工作面瓦斯涌出量的预测研究,提出了建立融合Piecewise混沌映射和Levy飞行策略的PLSMA-SVR模型,所提模型可行性通过陕西延安黄陵矿区4203综放工作面10个影响因素下的瓦斯涌出量数据进行了验证,并采取了与其余2种预测模型的对比分析,对比结果显示:3种模型下,PLSMA-SVR模型的预测结果误差率相对最小,且误差率平稳维持在较低水平;基础SVR模型误差率最大,最大一组误差率高达41.2%;DRSMA-SVR在基础模型上有所改进,效果也有所提升,但误差率依旧高于本文所提模型。综上所述,PLSMA-SVR预测模型在算法改进及预测结果、精度方面有显著提升,其可行性显而易见,有利于后续煤矿回采工作面瓦斯治理方面的运用,有助于增强煤矿安全性,工程意义较大。
