我国学前儿童体质生长曲线及评分标准的研制
2022-02-18涂春景张彦峰武东明江崇民
涂春景 ,张彦峰,武东明,王 欢,江崇民
中共中央、国务院于2016年印发并实施的《“健康中国2030”规划纲要》要求,开展国民体质测试,完善体质健康监测体系,开发应用国民体质健康监测大数据。自2000年以来,中国每5年进行1次国民体质测试。在体质评价方面,中国于2003年发布了第一个全国性国民体质评价标准《国民体质测定标准(幼儿部分)》(以下简称“2003年标准”)。“2003年标准”在较长时期内对中国体质监测工作起到重要指导作用,但随着体质研究的不断深入,逐渐显露出以下不足(国家体育总局,2003):1)在年龄纵向维度,该标准只提供了7个年龄段的离散型标准,而非连续性呈现,难以体现幼儿体质随年龄快速变化的生理特点。在同年龄段横截面维度,评分标准为等级制,没有考虑同等级内的个体差异和相邻等级间突变问题,无法进行精准的个性化评估。2)各指标评分标准制定方法比较简单,部分指标的百分位数波动较大,特别是时间序列指标的高位及低位百分位数。3)不便于制定在线测评系统。4)2000年至今,中国幼儿营养状况持续改善,幼儿体质发生了较大变化,如果继续使用“2003年标准”进行体质评价将会产生偏差。有研究表明,幼儿年龄段的“2003年标准”存在区分度不足(谢松林 等,2019)、无法进行个性化评价(全海英 等,2013,2016)等问题。由此可知,当前中国体质测评体系明显存在评价标准落后于测试的现状。鉴于此,应探索更加科学有效的标准制定方法,制定新的体质评价标准,完善中国幼儿体质健康测评体系。
百分位数曲线标准图表可以进行精准的个性化评估,在体质评价标准中得到广泛应用。世界卫生组织(World Health Organization, WHO)制定了 0~5 岁(WHO,2007)和 5~19 岁(Mercedes et al., 2007)儿童青少年百分位数曲线生长标准。21世纪国际胎儿和新生儿生长联合会(International Fetal and Newborn Growth Consortium for the 21stCentury, INTERGROWTH-21st)制定了胎儿和新生儿体质百分位数曲线标准(Papageorghiou et al.,2014;Villar et al.,2014)。美国(Kuczmarski et al.,2002)、荷兰(Cole et al.,1999)、乌克兰(Nyankovskyy et al.,2018)等国家先后制定了儿童体质百分位曲线标准。在中国,季浏等(2021)运用LMS法建立了中国7~22岁儿童青少年单项体质健康指标的百分位数曲线,并以C10、C50、C90为临界值划分体质健康的等级评分标准;首都儿科研究所运用LMS法建立了9个省会城市儿童青少年的身体形态指标百分位数标准曲线(李辉 等,2009;宗心南 等2020)。但鲜有基于全国的3~6岁幼儿体质百分位数曲线标准。
随着数理统计的发展和标准制定技术的进步,新的统计方法在体制标准研制中应用日趋普遍(杨桦 等,2020)。GAMLSS 模 型 法(generalized additive model for location,scale and shape)是当前国际上制定百分位数标准曲线的先进方法,该方法由Rigby等(2004)在LMS法(偏度-中位数-变异系数法)基础上创立,其既可对正态分布数据建模,也可对峰态分布或偏态分布的数据建模,包括对高度偏态分布和高峰度分布数据建模。由于GAMLSS模型在建立百分位数曲线方面的先进性,使其被广泛应用,多个国际组织和国家均运用GAMLSS模型制定了儿童体质健康指标的百分位标准曲线,如WHO儿童生长标准图表(Mercedes et al.,2007;WHO, 2007)、国际肺功能百分位标准曲线(Quanjer et al., 2012)等。在中国,GAMLSS模型已经应用于体质健康领域,如基于年龄和身高的中国儿童血压标准(范晖 等,2017)和中国3~6岁幼儿BMI百分位数曲线参考标准(涂春景 等,2021)等。
因此,本研究在“2003年标准”的基础上,运用GAMLSS 模型(Rigby et al., 2004; Stasinopoulos et al., 2018)构建中国3~6岁幼儿体质指标的百分位标准曲线,并根据所建百分位标准曲线划分等级,建立连续性的体质评分标准。
1 研究对象与方法
1.1 研究对象
1.1.1 建模数据来源
建模数据来自国家国民体质监测中心数据库,包括2010年和2014年国民体质监测得到的涵盖我国大陆31个省(自治区、直辖市)3~6岁幼儿体质数据。国民体质测试样本均按照分层随机整群抽样原则进行样本选取,即在各省域内按照经济发展水平分为一类、二类和三类地区,并分城乡、性别4类样本(国家体育总局, 2017)。
1.1.2 建模数据预处理
1.1.3 回代验证数据来源
考虑到验证样本应具有一定分散性以及数据获取的便利性,本研究回代验证数据采集了云南、四川、浙江和北京等4省份3~6岁幼儿体质数据。抽样原则、测试方法、质量控制等与历次国民体质监测一致(国家体育总局,2017)。其中,浙江省和北京市测试时间为2018年4月—2019年6月,云南省和四川省测试时间为2019年9—12月,测试仪器为健民牌II型体质测试器材,与国家国民体质监测中心一致。测试对象分为城镇幼儿、农村幼儿,按性别分为4类样本,以每1岁为1个年龄组。排除异常数据后,4省份分别得到有效样本量为:云南省(昆明市、普洱市和临沧市)2 261人(男1 137人、女1 124人),四川省(成都市、自贡市、广元市)2 286人(男1 140人、女1 146人),浙江省(杭州市、嘉兴市)2 728人(男1 381人、女1 347人),北京市(东城区、丰台区)2 426人(男1 282人、女1 144人),合计9 701人(男4 940人、女4 761人)。
1.2 研究指标
原始指标:身高、坐位体前屈、双脚连续跳、走平衡木、10 m折返跑、网球掷远和立定跳远。
派生指标:身高标准体质量。
1.3 研究方法
1)运用GAMLSS法构建体质指标百分位标准曲线。
2)体质指标评分标准制定方法:基于百分位标准曲线划分评分等级,运用插值法建立等级内连续性评分函数方程。
3)回代检验与评分实验:运用回代数据对所建模型进行有效性检验,并运用新旧标准进行评分比较实验。
2 建模过程与结果
2.1 基于GAMLSS模型构建体质指标百分位标准曲线
建模主要步骤:首先选择能反映原始数据本真的最优子模型,然后调节优化各参数曲线,最后建立百分位数曲线及其参考值。以双脚连续跳指标为例说明建模过程。
2.1.1 双脚连续跳指标的建模过程
2.1.1.1 样本特征值分析
中国3~6岁幼儿各年龄组双脚连续跳的均值、标准差、偏度和峰度等样本特征值表明(表1):男幼儿各年龄组的偏度系数范围为1.2~2.0,女幼儿各年龄组的偏度系数范围为1.1~2.2,均存在右偏;男幼儿各年龄组峰度系数范围为1.2~7.9,女幼儿各年龄组峰度系数范围为1.1~12.0,各年龄组峰度均为尖峰;各年龄组偏度和峰度正态性检验均具有统计学意义(P<0.05),故建模需要考虑原始数据存在偏度和峰度,而GAMLSS模型构建的百分位数曲线是由中位数(µ)、标准差(σ)、偏度(ν)和峰度(τ)4个参数曲线来表达,所以选择该模型构建百分位数曲线能较好地挖掘样本数据的原始信息。
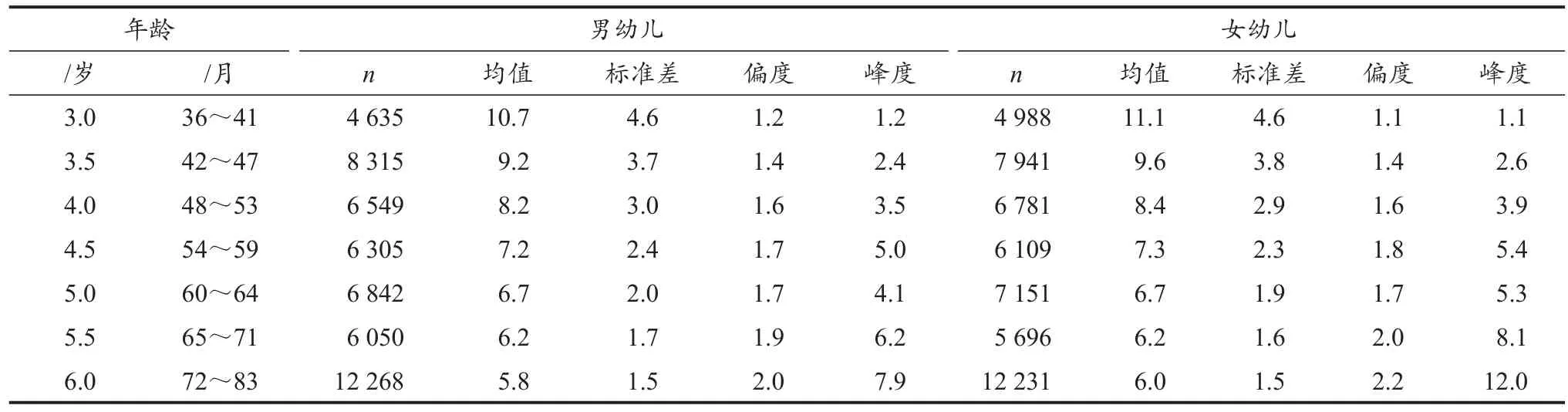
表1 建模样本人群双脚连续跳的特征值Table 1 Eigenvalues of Continuous Jumping with Both Feet of the Modeling Sample Population
2.1.1.2 最优子模型的选择和参数曲线调优
GAMLSS模型包含系列分布子模型,模型选择判断标准是依据赤池信息准则(Akaike information criterion,AIC)和 贝 叶 斯 信 息 准 则(Schwartz’s Bayesian criterion,SBC)。具体步骤:运用gamlss函数进行迭代运算,根据判断标准对运算结果进行比较(涂春景 等,2021; Rigby et al., 2004)。依此,本研究男、女幼儿最优子分布模型均为BCPEo (Box-Cox-Power-Expon.orig)模型,且模型幂转换系数ξ均为1.4。上述运算同时得出男、女幼儿参数µ、σ、ν、τ的初始自由度。
最佳曲线应兼顾曲线的光滑度和拟合度,而参数自由度大小是影响曲线光滑度和拟合度的核心因素。因此,本研究微调参数初始自由度,经比较后得到较优的模型自由度:男幼儿参数µ、σ、ν、τ的自由度分别为mu.df(µ)=6.65,sigma.df(σ)=5.06,nu.df(ν)=3.89,tau.df(τ)=3.69;女幼儿参数µ、σ、ν、τ的自由度分别为mu.df(µ)=6.66,sigma.df(σ)=5.52,nu.df(ν)=3.99,tau.df(τ)=5.64。
2.1.1.3 分布模型的参数拟合曲线方程
根据上述双脚连续跳的GAMLSS最优分布子模型和参数的自由度,得出参数拟合曲线方程。
1)男幼儿双脚连续跳分布模型为BCPEo,参数µ、σ、ν、τ的拟合方程为:
log(µ)=2.47-0.06cs(age^1.41,4.65)
log(σ)=-0.65-0.07cs(age^1.41,3.06)
ν=0.03-0.09cs(age^1.41,1.89)
log(τ)=-0.09-0.05cs(age^1.41,1.69)
2)女幼儿双脚连续跳分布模型为BCPEo,参数µ、σ、ν、τ的拟合方程为:
log(µ)=2.53-0.06cs(age^1.42,4.66)
log(σ)=-0.68-0.07cs(age^1.42,3.52)
ν=-0.07-0.09cs(age^1.42,1.99)
log(τ)=1.06-0.04cs(age^1.42,3.64)
2.1.1.4 双脚连续跳的百分位数曲线拟合优度检验
模型拟合效果定性诊断:男、女幼儿所建模型的残差核密度估计图近似正态分布图,残差Q-Q图上的绝大多数点近似分布在一条直线上(除远端少部分点离散),表明样本残差分位数与正态分布理论分位数比较吻合。
模型拟合效果定量诊断:男、女幼儿所建模型的残差平均数、方差、偏度和峰度均非常接近正态分布参考标准值。因此,男、女幼儿模型拟合优度符合要求。
2.1.1.5 双脚连续跳指标的百分位标准曲线和Z分标准值
1)男、女幼儿共同特征:百分位数曲线图的形状基本相似,C5与C95之间距离均随年龄增加而减小,且C90-C50>C50-C5;C50随年龄增加而减小,3~5岁减幅大,而5~6岁减幅小、曲线平缓,由此可知3~5岁是幼儿双脚连续跳成绩快速提高期。2)男、女幼儿不同特征:男幼儿百分位数均大于同年龄的女幼儿,且随年龄增加差距越来越小;女幼儿成绩随年龄增加提高更快(表2,图1)。
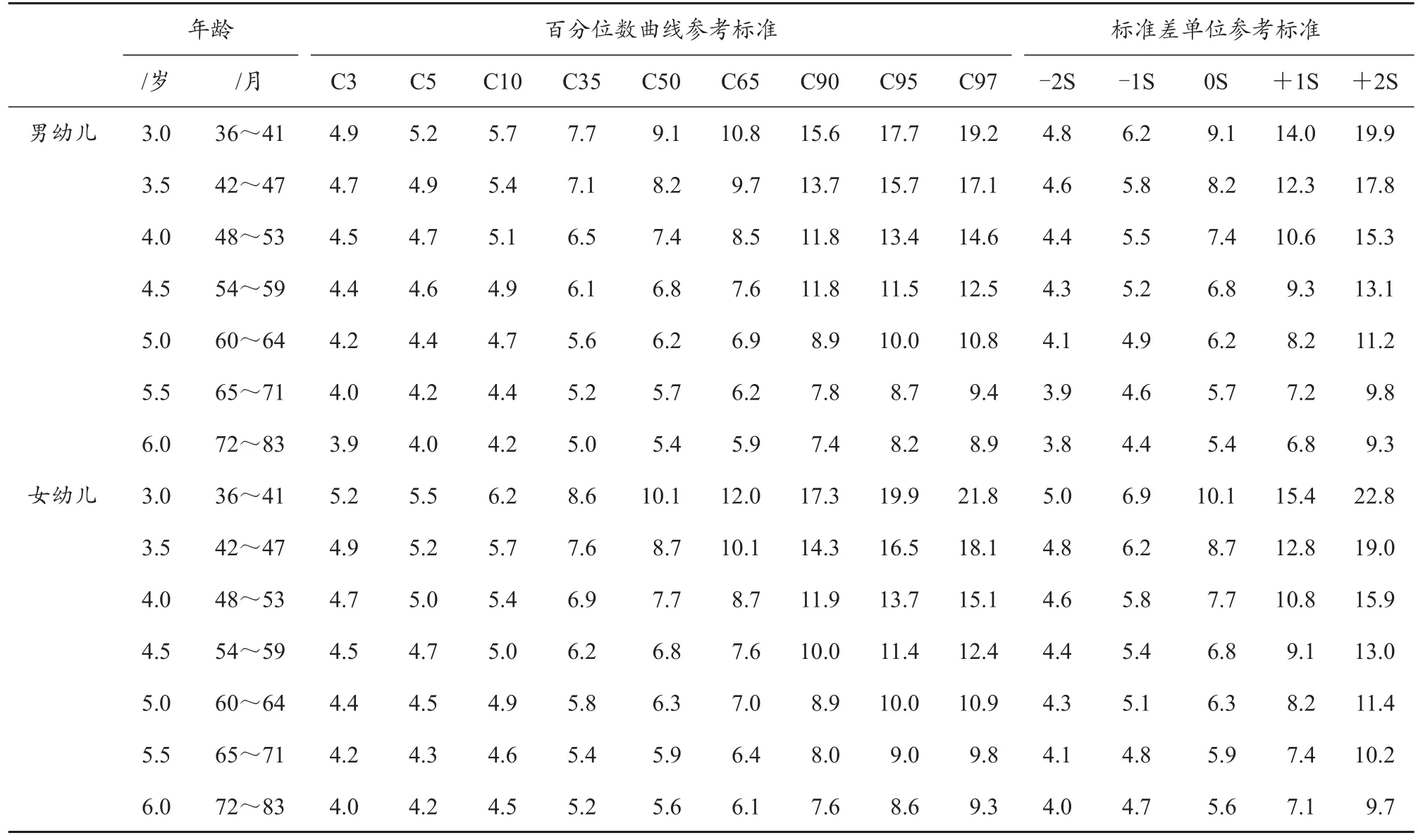
表2 中国3~6岁幼儿双脚连续跳的百分位数曲线参考标准和标准差单位值Table 2 Reference Standard for Percentile Curves and Standard Deviation Unit Value of Continuous Jumping with Both Feet of Children Aged 3 to 6 in China
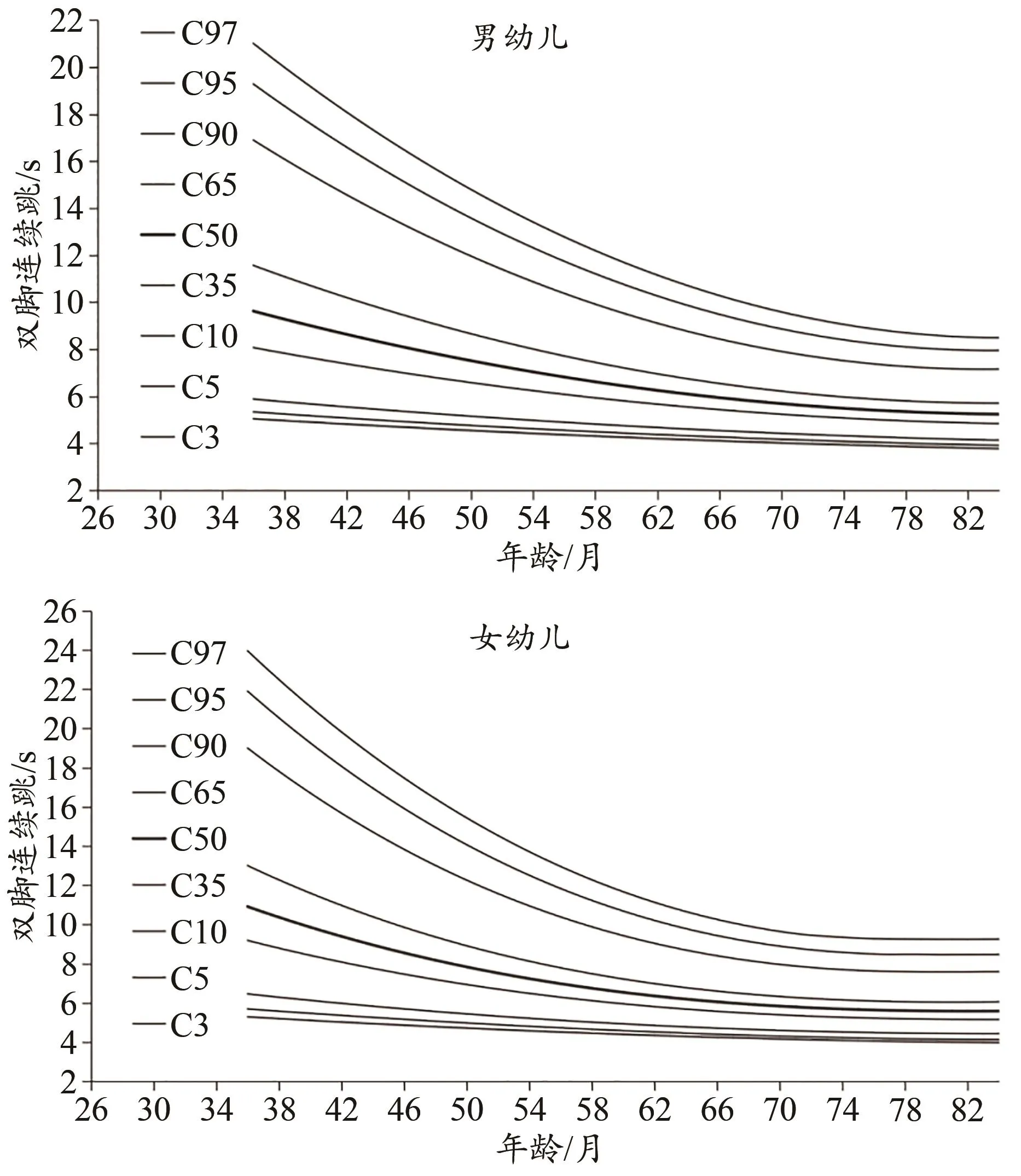
图1 中国3~6岁幼儿双脚连续跳的百分位标准曲线Figure 1. Percentile Standard Curves of Continuous Jumping with Both Feet of Children Aged 3 to 6 Years Old in China
2.1.2 其他体质指标百分位标准曲线的研制结果
根据“双脚连续跳”指标研制过程与方法,身高标准体质量Z分标准曲线①因身高标准体质量评分标准以Z分标准值划分等级,所以此处提供Z分标准曲线图。如图2所示,其余各指标的百分位标准曲线参考值如表3所示,考虑到篇幅,此处未逐一列出各单项体质指标百分位数曲线图。
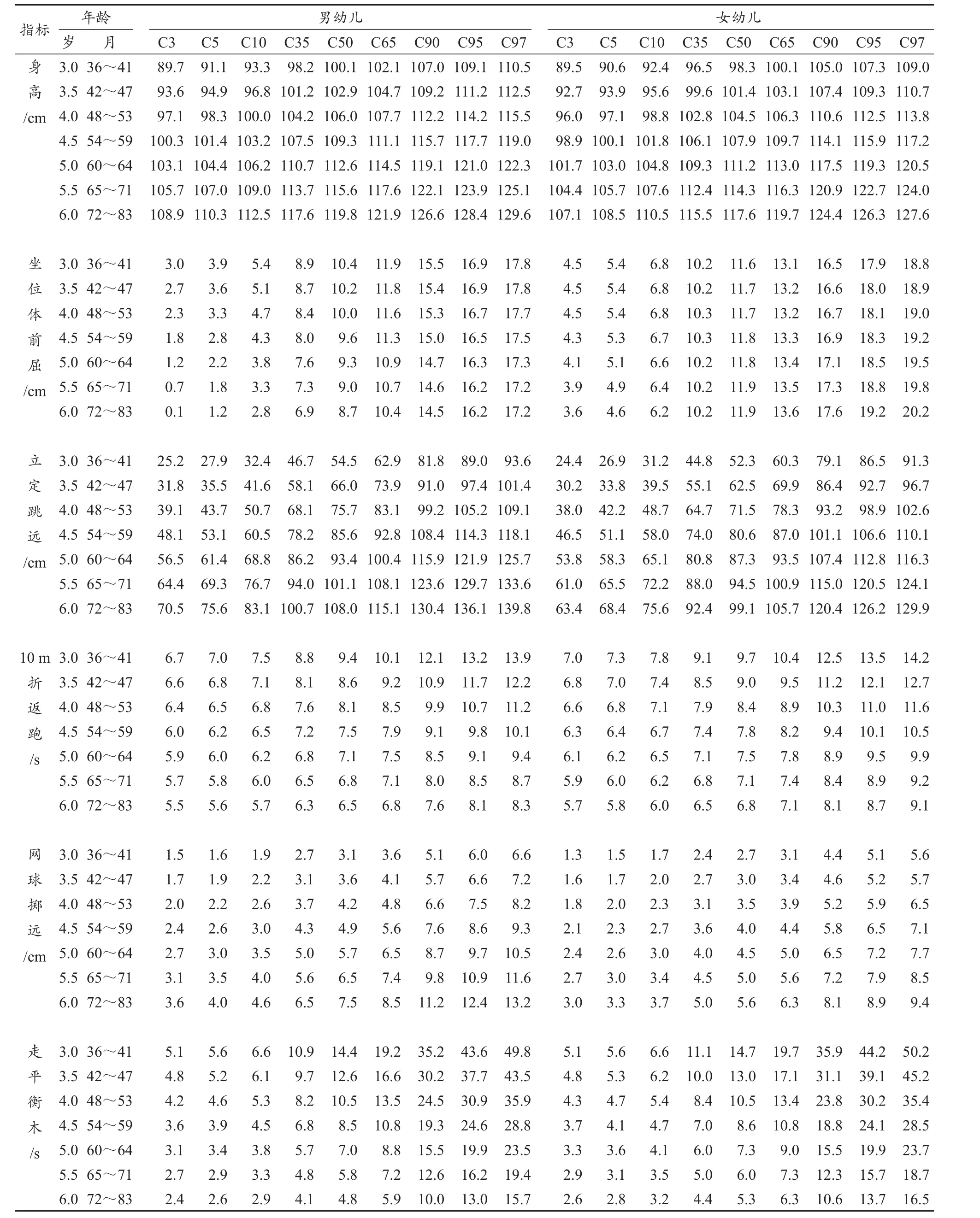
表3 中国3~6岁幼儿体质指标百分位标准曲线参考值Table 3 Reference Values of Percentile Standard Curves of Physical Fitness Indexes of Children Aged 3 to 6 Years Old in China
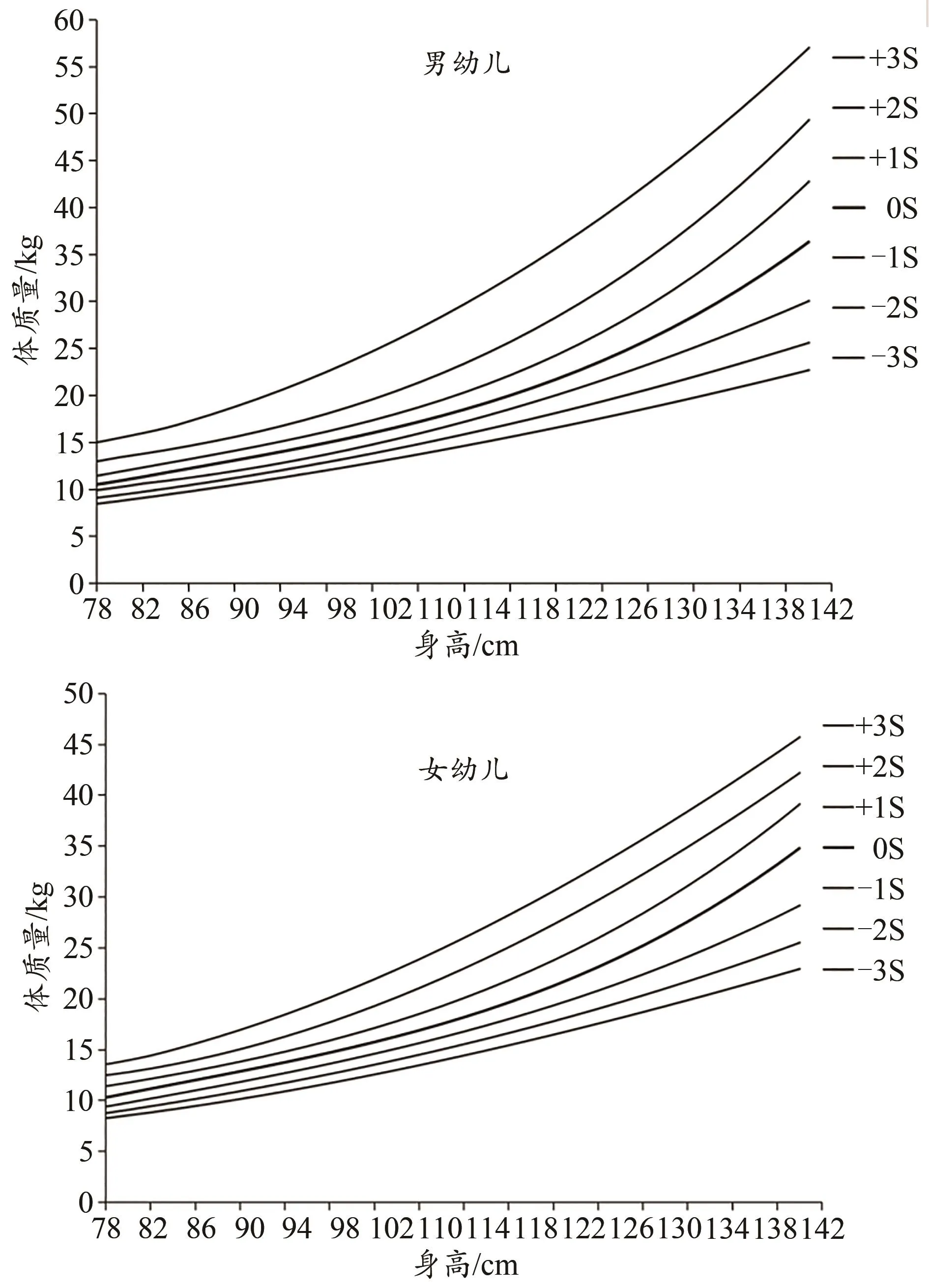
图2 中国3~6岁幼儿身高标准体质量Z分标准曲线Figure 2. Z-Score Standard Curves of Weight-for-Height of Children Aged 3 to 6 Years Old in China
拟合效果检验发现,各体质指标所建模型的残差核密度估计图近似正态分布,残差Q-Q图上的点近似在一条直线上;定量检验中平均数、方差、偏度和峰度的残差均非常接近正态分布参考标准,拟合效果符合要求。
2.1.3 回代检验
建模过程中已对模型的拟合效果进行了定性与定量两方面检验,检验结果良好。同时,考虑到参考标准是为了实践应用,采用2018—2019年实测数据对百分位标准曲线进行回代检验,比较回代数据在所建百分位标准曲线下分布与实际分布的一致性,验证有效性。
按照已建立的百分位数曲线,统计样例在C10、C35、C65和C90以下的百分数。回代检验结果表明,身高、体质量等7个原始指标百分位下的例数与实际例数的差异率男幼儿为-2.5%~1.9%、女幼儿为-3.4%~2.9%,派生指标身高标准体质量差异率男幼儿为-1.1%~1.3%、女幼儿为-0.7%~1.5%。由此可知,各年龄组差异率都在5%以下,进一步统计所有差异率,发现在1%以内的占80%。相关研究表明,回代检验差异率在5%以下为合格(练碧贞 等, 2019;席翼 等, 2013)。因此,本研究所建百分位标准曲线一致性良好。
2.2 各单项体质指标评分标准的制定
依据体质指标百分位标准曲线,以特定百分位数曲线作为划分评分等级的临界值,进行等级赋分,并建立每个等级内连续性评分函数方程。
2.2.1 各等级临界值划分方法
考虑新评分标准与“2003年标准”的连续性,本研究采用5分等级制评分法,且各等级临界值沿用“2003年标准”划分方法(江崇民 等,2004)。具体评分如下:身高标准体质量指标按照-2S、-S、+S、+2S标准差为临界值,即[-3S,-2S]和[2S,+3S]为1分、[-2S,-S]和[+S,+2S]为3分,[-S,+S]为5分,其余体质指标以C10、C35、C65和C90等4条百分位数曲线划分各等级。其中,高优指标[C0,C10]为1分、[C10,C35]为2分、[C35,C65]为3分、[C65,C90]为4分、≥C90为5分;低优指标≥C90为1分、[C65,C90]为 2 分 、[C35,C65]为 3 分 、[C10,C35]为4分、[C0,C10]为5分。评分结果反映被评价者的某项指标在该年龄点所处位置,评分越高说明体质水平越好。
2.2.2 构建各等级区间内的连续性评分函数方程
参照相关研究等级内部评分方法(王国军,2013),本研究运用Z分插值法制定各等级内部连续性评分函数。例如,高优指标3分,其Z分区间为-0.385~0.385,对应的百分位数为C35~C65,其Z分法连续性评分公式为:
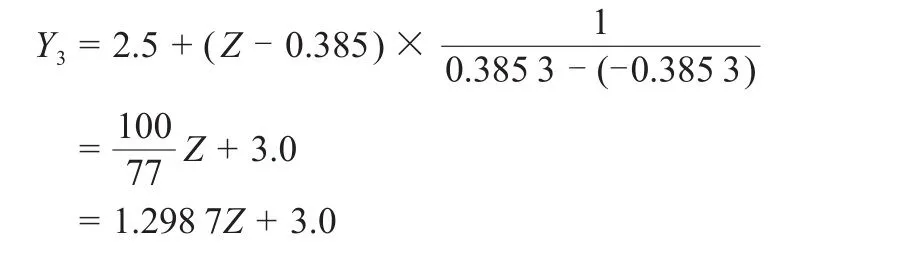
按此方法可得各等级结果如下。
1)高优指标,按等级分区间,Z分法连续性评分公式为:
1分,对应-3≤Z≤-1.282,Y1=0.872 9Z+2.62
2分,对应-1.282≤Z≤-0.385,Y2=1.115 7Z+2.93
3分,对应-0.385≤Z≤0.385,Y3=1.298 7Z+3.07
4分,对应0.385≤Z≤1.281 6,Y4=1.115 7Z+2.93
5分,对应1.281 6≤Z≤3,Y5=0.581 9Z+3.75
2)低优指标,按等级分区间,Z分法连续性评分公式为:
1分,对应1.282≤Z≤3,Y1=-0.872 9Z+2.62
2分,对应0.385≤Z≤1.282,Y2=-1.115 7Z+2.93
3分,对应-0.385≤Z≤0.385,Y3=-1.298 7Z+3.07
4分,对应-1.282≤Z≤-0.385,Y4=-1.115 7Z+2.93
5分,对应-3≤Z≤-1.281 6,Y5=-0.581 9Z+3.75
3)中优指标(身高标准体质量),评分公式为:
1分,分 2种情况:当-3≤Z≤-2时,Y1右=2×Z-6;当2≤Z≤3时,Y1左=-2×Z+6
3分,分 2种情况:当-2≤Z≤-1时,Y3左=2×Z+6;当1≤Z≤2时,Y3右=-2×Z+6
5分,分 2种情况:当-1≤Z≤0时,Y5左=1.5×Z+5;当0≤Z≤1时,Y5右=-1.5×Z+5
根据上述评分方法,评分步骤为:在各单项指标百分位数曲线图表(或Z分值图表)中,通过年龄和体质成绩查找个体成绩在图表中对应的百分位数,再将百分位数根据标准正态分布表转换为Z值,并代入Y与Z分的函数方程,即可得出个体体质指标的评分结果。
3 分析与讨论
3.1 本研究构建的百分位标准曲线特征
1)百分位标准曲线特征。研究结果显示,各体质指标成绩随年龄增长而提高,其中“低优指标”(如双脚连续跳和走平衡木等)百分位数曲线随年龄增加由高到低,“高优指标”(如网球掷远和立定跳远等)则相反,因此,各体质指标(除坐位体前屈之外)随年龄增长均呈正向变化,与已有研究结论一致(马宇飞 等,2014;周喆啸 等,2020)。本研究结果与WHO(2007)的身高C50参考值比较可知,男、女幼儿各年龄平均差值比WHO分别高1.3 cm(1.2%)、0.7 cm(0.6%),存在这种差异原因可能与样本数据采集时间和国家有关。虽然存在上述差异,但本研究身体形态指标百分位图与WHO(2007)儿童生长发育标准图在形态上具有相似的变化趋势。
2)百分位数曲线性别差异分析。通过比较男、女幼儿C50的参考值可知,男幼儿身高、双脚连续跳、10 m折返跑、网球掷远、走平衡木、立定跳远均优于女幼儿,男、女幼儿差值分别为 1.6 cm(1.5%)、0.3 s(4.0%)、0.3 s(4.1%)、1.0 cm(24.0%)、0.3 s(3.3%)、5.2 cm(6.4%),但男幼儿坐位体前屈比女幼儿差2.2 cm(18.4%)。这说明幼儿时期部分体质指标已显现出性别差异,与已有研究结论一致(徐伟 等,2018;Latorre et al.,2017)。
3.2 本研究百分位数曲线和“2003年标准”百分位数比较
以男幼儿10 m折返跑指标为例,对比本研究百分位数曲线标准和“2003年标准”等级划分的百分位数(图3)。
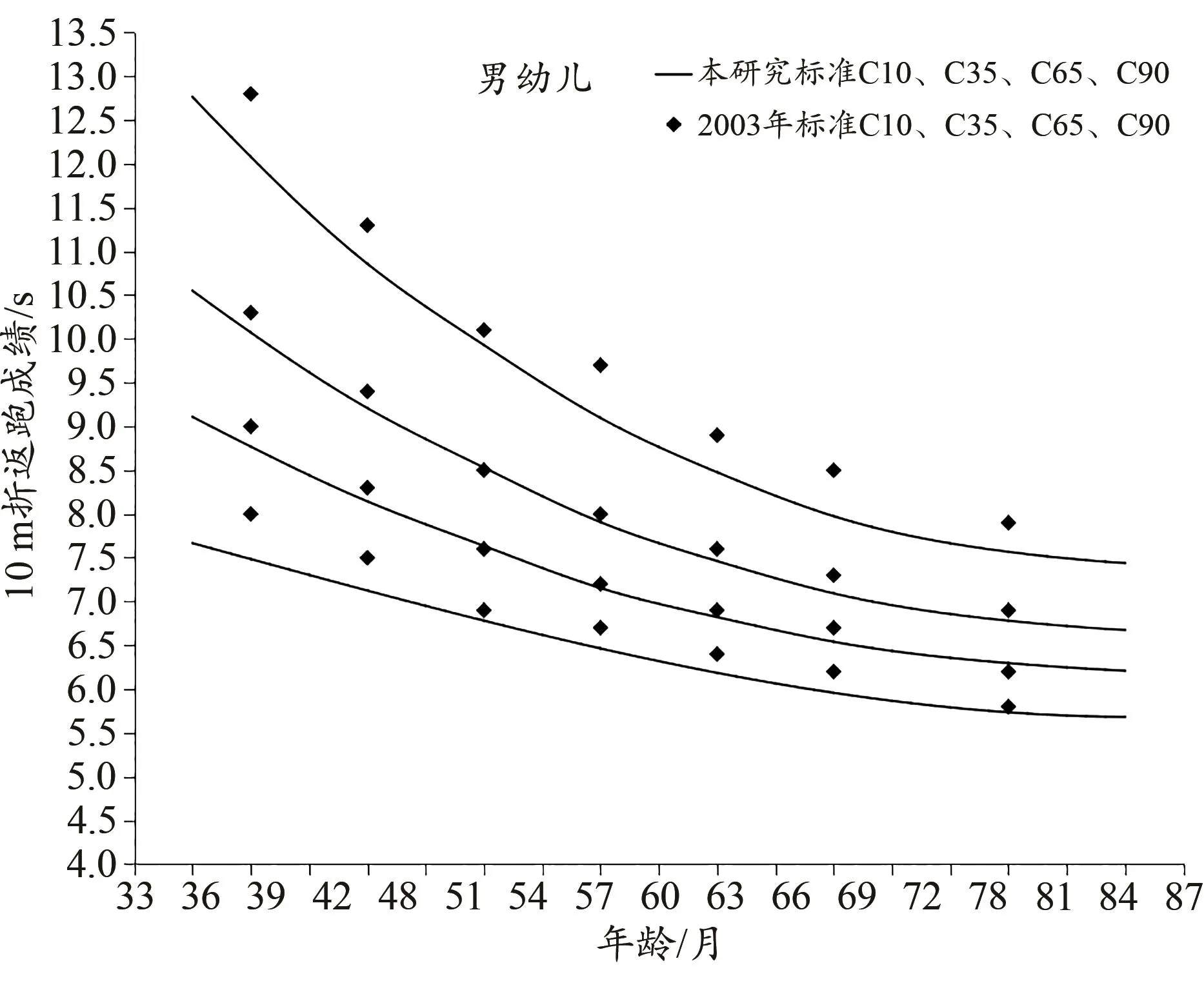
图3 本研究10 m折返跑百分位标准曲线与“2003年标准”对比Figure 3. Comparison of the Percentile Standard Curves of the 10 m Shuttle Run between the Current Study and the“ 2003 Standard”
1)本研究标准在年龄纵向维度上提供了精准化评价结果,即任意年龄点的百分位数参考值。自变量年龄以“日”“月”为单位的参考标准,能体现幼儿时期生理机能随年龄增加而快速变化的特点;而“2003年标准”只提供了3.0、3.5、4.0、4.5、5.0、5.5和6.0岁共7个年龄组的百分位数参考值,无法区分不同月龄的体质差异,忽略了同年龄不同月龄幼儿生理变化的特点。2)本研究标准在横截面维度上提供了精准化评价结果,在同年龄横截面上提供了任意百分位数,如第1.1百分位、第2百分位、第99.9百分位等,而“2003年标准”只提供了第10、35、65和90等有限数量百分位数。3)本研究标准曲线平滑,误差较小;而“2003年标准”波动大,各年龄组间变化不稳定,尤其是高位和低位百分位数,如C95和C5。4)本研究制定的百分位数标准曲线可以划分评价等级,如以C35、C65、C90作为不及格、合格、良好和优秀的临界值或临界线。更为重要的是,其还可用于重要健康标准的划分,制定健康预警标准。
使用本研究标准和“2003年标准”对其余各体质指标进行对比,也得到类似结论。
3.3 本研究评分标准与“2003年标准”评分标准比较
为了比较本研究评分标准与“2003年标准”在实际应用中的差异,随机选取回代验证数据中的16名幼儿(男、女幼儿各8名,其中A1~A8为男幼儿,B1~B8为女幼儿,年龄为月龄),以低优指标10 m折返跑为例进行评分实验。结果表明,B4、B5 2名幼儿10 m折返跑成绩分别为8.1、6.9 s,采用本研究标准对B4、B5 评分结果分别是2.5和3.2分,而按照“2003年标准”均为3.0分(表4)。其他指标也有类似的结论。因此,相比于“2003年标准”,本研究标准既能够个性化评分又兼顾等级评分,能更准确反映中国幼儿的体质健康现状。
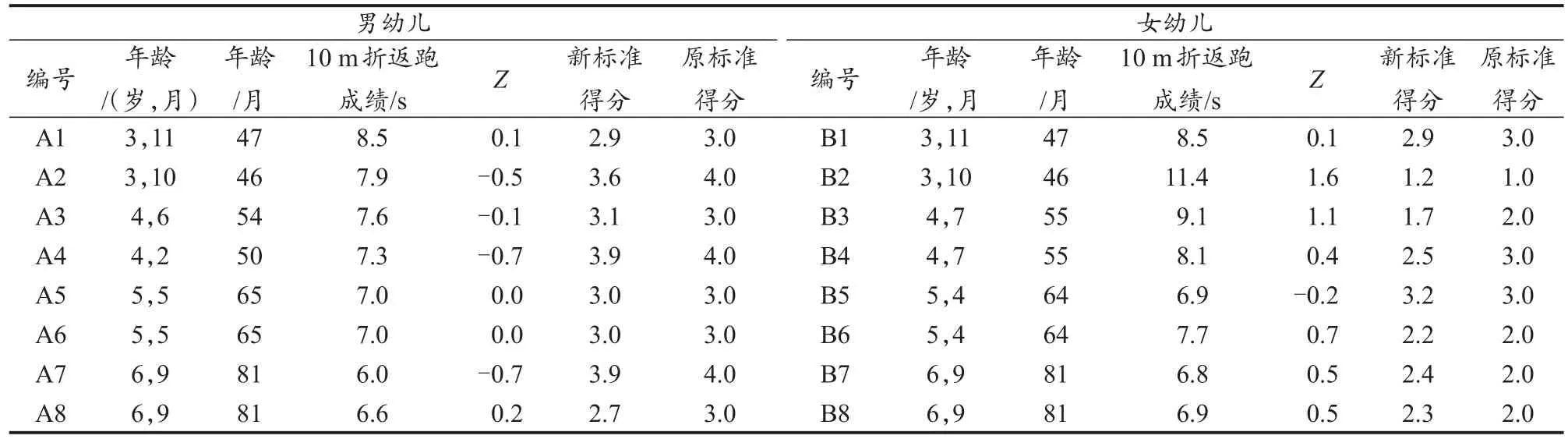
表4 本研究10 m折返跑评分标准和“2003年标准”评分标准比较Table 4 Comparison of the Scoring Standard of the 10 m Shuttle Run between the Current Study and the “2003 Standard”
4 结论与展望
4.1 结论
1)本研究基于GAMLSS模型的构建了各体质指标百分位数参考标准图表及相关参数方程,所建百分位标准曲线光滑稳定,检验表明模型的拟合优度较优,回代检验也显示应用模型进行评价有较高的有效性。
2)本研究结果优化了“2003年标准”在纵向维度和横截面维度上非连续、波动大、等级间突变等问题。建立的评分标准同时提供了各体质指标等级评分标准和等级内的连续性评分方程,达到了提供个性化评价标准的目标。
3)本研究基于全国国民体质监测数据,样本量大、代表性广,结合GAMLSS模型建立百分位标准曲线以及兼具现实性和前瞻性的个性化评价标准,在评价我国3~6岁幼儿体质健康时可参考使用。
4.2 展望
本研究验证了GAMLSS模型在制定单项体质指标百分位数曲线参考值以及在制定百分位数曲线方面具有优越性和普适性,可推广应用于其他体质指标参考标准或未来新增指标参考标准的制定。同时,也可结合学龄儿童甚至成年人、老年人建立更长年龄区间的百分位数曲线标准,以便纵向追踪个人体质发展历程与趋势。未来可结合当前5G科技成果,进一步开发智能化在线体质健康监测平台,通过5G手机端即可实现个体或群体单项指标精准评分。
