流化床煤气化过程参数不确定性量化
2022-02-18吴士龙
吴士龙
(河南理工大学能源科学与工程学院,河南焦作454000)
通过气化清洁高效地使用煤炭被认为是确保能源市场对这种燃料的持续需求的一种有希望的替代方法[1]。这项技术的特点是通用性强,可以使用多种燃料以及对产品开放的各种应用。产生的合成气可用于发电、化学原料、氢气等[2]。煤气化是一种成熟的生产合成气(H2+CO)的技术,建立煤气化过程的代理模型对于理解操作参数对气化性能的影响和优化过程性能及确定操作条件是重要的。Kriging代理模型具有高度拟合的优点,已经被广泛使用[3]。另外蒙特卡洛模拟也是进行不确定性量化分析的一个重要方法[4]。在这项工作中,研究的目标是:评估操作参数的波动性对合成气产量的影响。
1 数据和方法
1.1 煤气化数据
在Kriging代理模型的建立过程中使用了印度的燃料研究所在文献中公布的煤气化数据以及煤的性质[5]。煤的性质如表1所示,煤气化数据如表2所示。

表1 煤性质
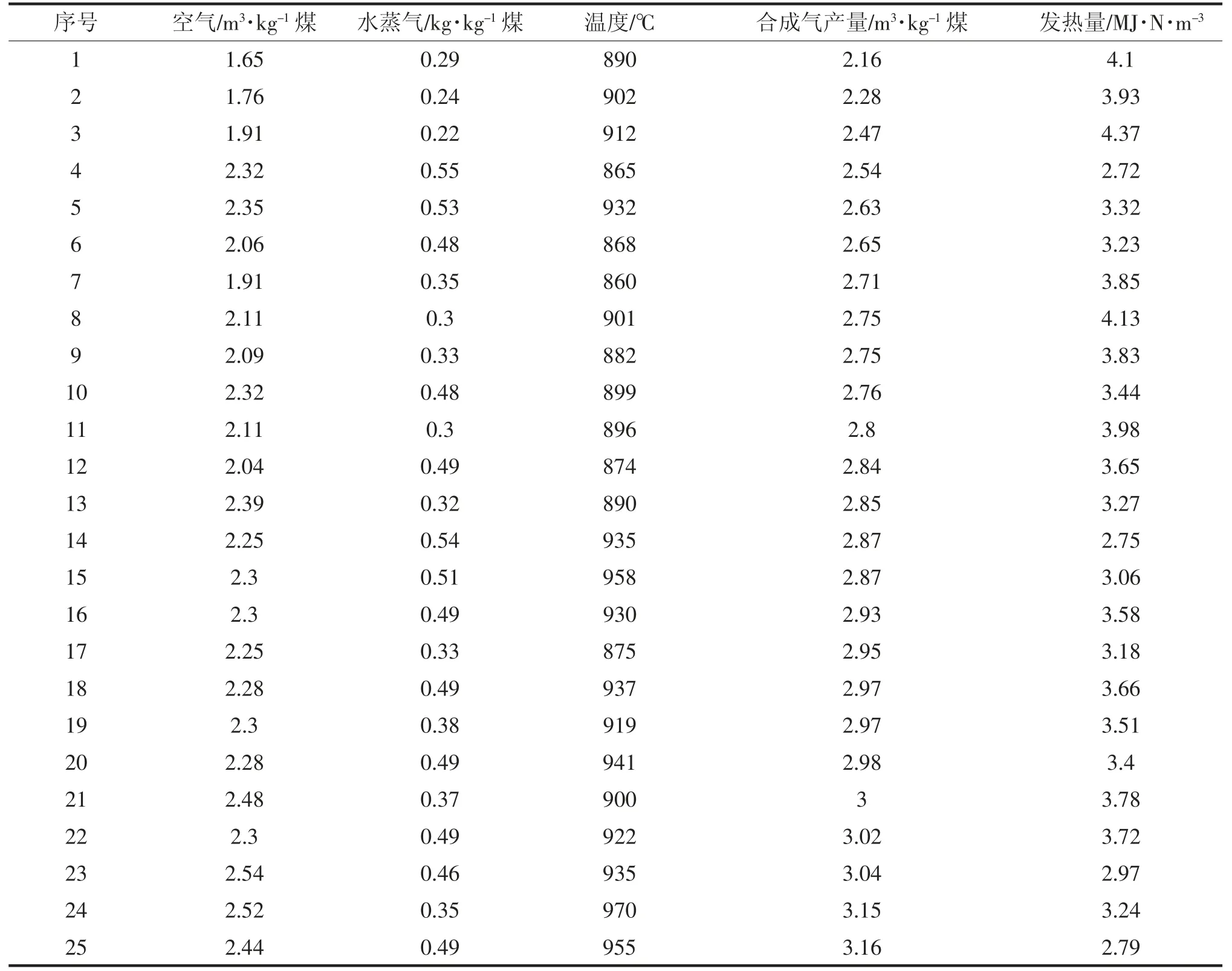
表2 煤气化数据
1.2 Kriging代理模型
高压煤气化技术的主要优点之一是产生的合成气可用于多种应用。为此,该过程可用于优化不同的响应变量。因此,在煤气化过程中,最重要的变量是合成气产量。同时,还必须考虑发热量,发热量的高低代表了煤的燃烧是否充分,发热量越高代表煤燃烧越充分。
Kriging模型是一种插值模型,由Danie G.Krige开发,最早用于用于预测采矿孔[6]。随后Sacks等[7]将其引入计算机实验。为了检验代理模型对实验数据拟合的统计显著性,通过方差分析来对其进行检验。
1.3 蒙特卡洛模拟
蒙特卡洛模拟[8,9]也称计算机随机模拟,是以随机数集为基础的一种概率统计方法。蒙特卡洛模拟作为统计学模型工具,可以在使用时进行模拟仿真上万次,这相对于进行试验或者进行大型的计算机仿真来说非常的便捷。可以在使用时模拟仿真数千至上万次,模拟一次相当于做了一次煤气化过程的实验。
2 结果与讨论
2.1 代理模型
建立关于合成气产量和发热量的Kriging代理模型,我们将其代理模型通过图1和图2来对其进行直观地表示。通过计算得出关于合成气产量的方差为0.215%,发热量的方差为0.199%,表明所建立的代理模型精度能够满足接下来的研究。

图1 合成气产量代理模型三维图
2.2 全局灵敏度分析
作为不确定性量化评估的一部分,基本分析之一是全局敏感性分析。它旨在回答以下问题:对于给定的参数空间,哪些输入因素对观察到的感兴趣的量的可变性影响最大,因此可以分配有限的资源来减少这些输入因素的不确定性。在传统的灵敏度分析中,设计空间中固定点的梯度(通常为平均值)用于评估单个因素的灵敏度,这提供了非常有限的灵敏度视图。因此,全局灵敏度提供了整个设计空间中灵敏度的整体视图,从而为设计提供了完整的覆盖范围。
作为不确定性量化评估的一部分,基本分析之一是全局敏感性分析。它旨在回答以下问题:对于给定的参数空间,哪些输入因素对观察到的感兴趣的量的可变性影响最大,因此可以分配有限的资源来减少这些输入因素的不确定性。在传统的灵敏度分析中,设计空间中固定点的梯度(通常为平均值)用于评估单个因素的灵敏度,这提供了非常有限的灵敏度视图。因此,全局灵敏度提供了整个设计空间中灵敏度的整体视图,从而为设计提供了完整的覆盖范围。
根据上面的数据建立了Kriging代理模型,在该代理模型上进行了全局灵敏度分析。表3给出了全局灵敏度分析的结果,结果表明对合成气产量产生的主要影响是操作参数的变化而不是参数之间的相互作用,其中空气流量对合成气质量的影响最大,占比为63.95%,水蒸气占比为18.41%,温度占比为12.96%;此外,参数之间的相互作用只有空气与水蒸气之间的相互作用大于1%,为4.6%。
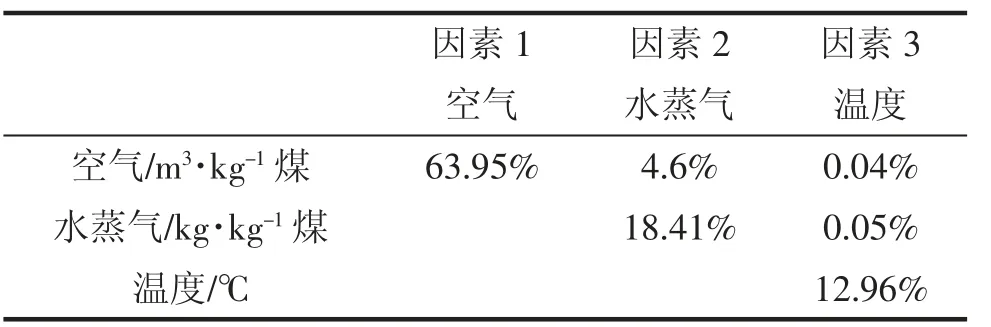
表3 参数对合成气产量的贡献
2.3 不确定性传播
不确定性的正向传播分析了输入变量的不确定性对感兴趣参数数量的影响。使用的方法为蒙特卡洛,我们此节是为了说明参数的波动性对合成气产量的影响。值得注意的是,这些参数的波动性是不容易测量的,因此我们只能假设参数是保持不变的或者是波动的并赋予其一个概率密度函数(PDF)。表4、表5展示了我们所假设的几种参数分布情况。
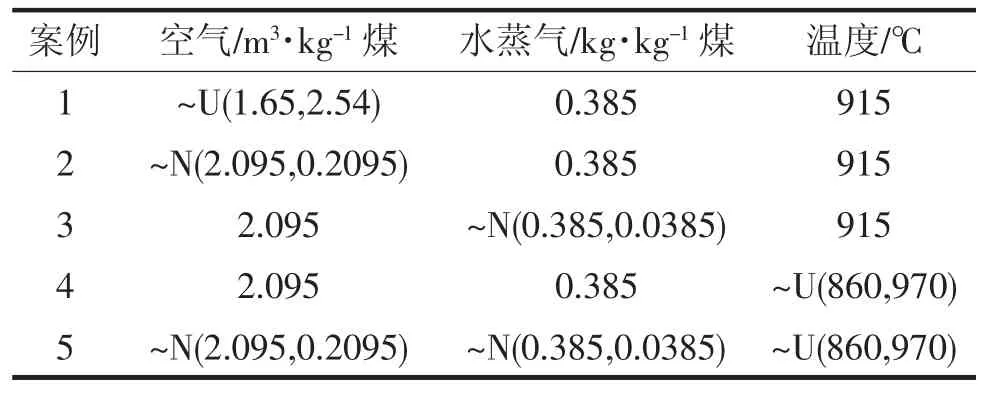
表4 不确定性案例
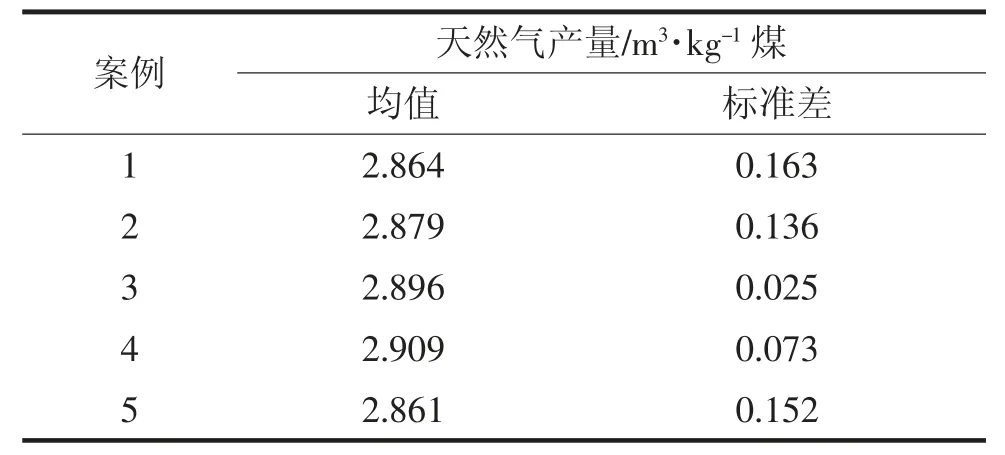
表5 天然气产量均值与标准差
从表3和图2可以看出:空气流量对于天然气产量有着重大影响,根据图2的不确定性分析结果,在给定规定的操作参数不确定性的情况下,评估天然气产量达到2.9(m3/kg煤)的概率,我们会得到不同结果。对于案例1,空气流量的概率密度函数为均匀分布,天然气产量达到2.9(m3/kg煤)的概率为0;对于案例2,空气流量的概率密度函数是均值为2.095方差为0.2095的正态分布,天然气产量达到2.9(m3/kg煤)的概率为62.14%;对于案例3,水蒸气流量的概率密度函数是均值为0.385方差为0.0385的正态分布,天然气产量达到2.9(m3/kg煤)的概率为100%;对于案例4,温度的概率密度函数是均匀分布,天然气产量达到2.9(m3/kg煤)的概率为66.22%;对于案例5,空气流量的概率密度函数是均值为2.095方差为0.2095的正态分布,水蒸气流量的概率密度函数是均值为0.385方差为0.0385的正态分布,温度的概率密度函数是均匀分布,天然气产量达到2.9(m3/kg煤)的概率为69.74%。
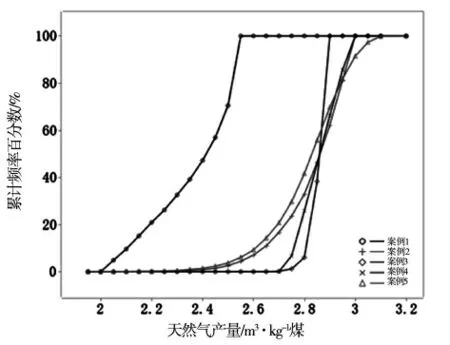
图2 天然气产量经验累积分布图
3 结论
不确定性量化在煤气化中的应用是通过现有的煤气化数据集对实验中适用的条件来进行模拟,输入参数和目标函数是固定的。我们通过原始数据建立了Kriging代理模型,在该模型的基础上进行了全局灵敏度分析,得到了空气、水蒸气和温度以及它们之间的相互作用对天然气产量的影响,此外进行了参数的不确定性传播,并用概率密度函数表示它们,结果表明参数的不同分布情况下天然气产量达到某一概率密度的概率不同。
