考虑焊料空洞损伤的IGBT双向热网络模型

蔡彦阁，杜明星，姚婉荣

（1.天津理工大学 天津市复杂系统控制理论及应用重点实验室，天津 300384；2.天津中科华盈科技有限公司，天津 300300）

0 引言

近年来，电力电子装置在电动汽车、风力发电、航空航天等领域广泛应用。而功率器件作为电力电子装置的核心[1]，由于长时间工作在高温环境中，其可靠性受到了一定的制约。因此，提高功率器件的可靠性是决定系统能否稳定运行的关键。IGBT 模块的封装级失效类型主要有键合线失效和焊料层失效，而焊料层失效主要是由于焊料层中出现空洞和裂纹损伤所致。在模块封装过程中，当空气中的气泡嵌入环氧材料就会在焊料层产生空洞[2]。尽管新的焊料工艺可以有效地限制焊料层空洞产生，但不能完全消除它[3]。在IGBT 模块工作中，焊料层承受热应力也会产生空洞损伤。

Bladimir 等人研究了焊料层中实际空洞率与导热系数关系，并将空洞对焊料层温度产生的影响进行评估[4]。陈民铀等人提出了计及焊料层疲劳的IGBT 模块寿命评估，研究高频下芯片焊料层与DBC 焊料层分别出现老化时对结温的影响[5]。文献[6]通过有限元仿真，研究去除硅胶和外壳的IGBT 模块在出现空洞损伤时芯片结温分布，并建立了考虑空洞损伤的Cauer 模型。焊料层损伤会减小热流路径，使更多热流集中在空洞附近，降低IGBT 模块的散热性能，导致结温升高，进而加快模块的老化过程。故研究焊料层空洞对IGBT 芯片温度分布的影响，以及准确监测老化后IGBT 模块的结温具有重要意义。然而，热量在模块内部传递时受其物理结构的影响[7]，硅胶和外壳是模块的重要组成部分，会对热流传递产生影响。很多研究成果仅仅专注于芯片及其下层结构对热流传递的影响[5-7]，导致热仿真模型和热网络模型与实际模块结构不相符，然而考虑硅胶和外壳的模型更为真实。因此，本文研究当焊料层出现空洞损伤时，硅胶和外壳对IGBT 芯片温度的影响。

1 IGBT模块的热模型

本文以型号为WGL100B65F23 的模块作为研究对象，表1 是各层状结构的尺寸，表2 是各层材料的参数。

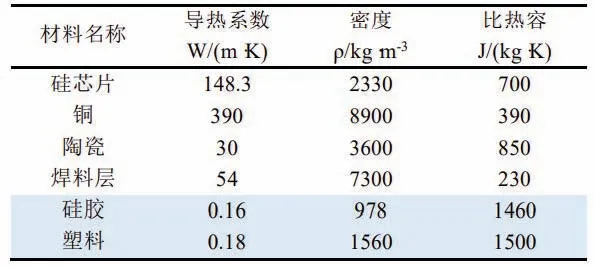
表2 IGBT模块各层材料的参数Table 2 Material parameters of each layer of IGBT module

为研究芯片焊料层空洞对结温的影响，选取定制的焊料层空洞率为5.5%、9.4%和15%的模块作为研究对象，图1 是其芯片焊料层的X 光照片。

图1 芯片焊料层空洞分布图Fig.1 Void distribution map of chip solder layer

1.1 传统模型

传统Cauer 模型忽略了硅胶和外壳对温度的影响，只包括芯片及其下层结构。每一层结构用一对热阻和热容来表示。

由于空洞中充满空气或为真空状态，当芯片焊料层出现空洞时，其热阻值增大，热容值减小，散热性能下降，导致模块结温升高。为计算芯片焊料层出现空洞后的准确结温，需建立考虑空洞损伤的Cauer 模型。

图2 所示为健康模块和老化模块的有效传热区域示意图。为清楚表示空洞对有效传热面积的影响，假设焊料层出现了一个面积较大的空洞，将焊料层分成左右两部分。由于空洞的传热能力远小于焊料，可以将空洞近似为绝热。由空洞隔开的两部分焊料层对于其下层结构来说是两个邻近的热源，热量向下传播时有效传热面积以一定的角度扩大，两部分焊料层的有效传热区域出现耦合。交叉部分的温度高于其他有效传热区域，因此在空洞上方的芯片处出现高温区域。

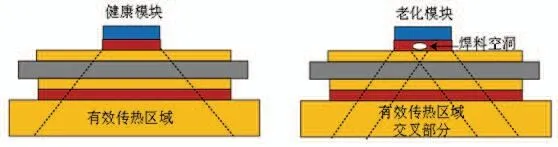
图2 健康和老化模块的有效传热区域对比Fig.2 Comparison of effective heat transfer area of healthy and aging modules

本文主要研究焊料层出现空洞时的情况，因此在建立仿真模型时忽略键合线以及接线端子的影响。在有限元仿真过程中，将模块底部的温度设置为室温，通过设置边界条件来模拟散热器，假设续流二极管不发热，通过在IGBT芯片上施加功率损耗来模拟模块工作时芯片的产热，根据表2 所给的数据设置模块各层状结构的参数。

健康和出现空洞损伤的模块中未考虑硅胶和外壳的有限元仿真模型的芯片温度分布，如图3 所示。健康模块的芯片的中央位置温度最高，向四周呈递减趋势，中心到边缘的温度梯度较小，红色的高温区域较大，温度分布均匀。当芯片焊料层出现空洞时，随着空洞率的升高，芯片的最高温度增大。芯片的最高温度由芯片中央转移到空洞集中或较大面积空洞的上方，芯片的高温区域减小，中心到边缘的温度梯度增大。仿真结果与上文的理论分析一致。

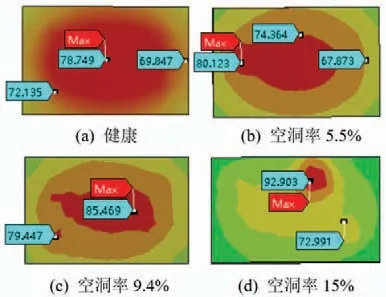
图3 未考虑硅胶和外壳的仿真模型的芯片温度分布Fig.3 The chip temperature distribution of the simulation model without considering the silicone and shell

传统热网络模型在计算热阻和热容时，并未考虑有效传热区域的耦合现象。健康模块的热量分布均匀，用这种方法计算有效传热面积时不会产生较大误差。当芯片焊料层出现空洞时，这种计算方法会使热阻热容值与实际情况相差较大，进而使热网络模型计算的结温出现较大误差。但由于空洞位置和大小的随机性，很难实现在实际工况中考虑空洞对有效传热区域的影响。而经过热仿真发现，硅胶和外壳可以使结温分布均匀，在建立热网络模型时可忽略空洞对有效传热区域的影响。因此，本文建立考虑硅胶和外壳的双向热网络模型，以逼近实际的物理工况。

1.2 双向热网络模型

焊料层出现空洞时，考虑硅胶和外壳的热网络模型如图4 所示。由于此模型同时考虑了芯片的上、下层结构，因而称之为双向Cauer 模型。基于传统Cauer 模型的原理，分别用一对RC 来表示硅胶和外壳的热阻和热容，其数值见表3。

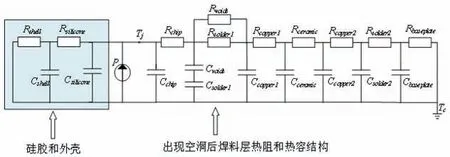
图4 考虑空洞损伤的双向Cauer模型Fig.4 Bidirectional Cauer model considering void damage

表3 热网络模型的RC参数Table 3 RC parameters of the thermal network model

图5 是考虑硅胶和外壳的IGBT 模块的有限元分析模型，图6 为考虑硅胶和外壳的仿真模型的芯片温度分布。健康模块的芯片温度分布与不考虑硅胶和外壳时的芯片温度分布接近。而当焊料层出现空洞时，硅胶和外壳可以减小芯片温度分布受空洞的影响，最高温度更接近芯片的中央位置，较大面积的空洞上方位置的温度均匀，芯片高温区域较大，温度梯度较小。由于芯片温度分布均匀，在计算热网络模型的热阻和热容时，可忽略空洞对有效传热面积的影响。

图5 考虑硅胶和外壳的有限元仿真模型Fig.5 Finite element simulation model considering silicone and shell

图6 考虑硅胶和外壳的仿真模型的芯片温度分布Fig.6 The chip temperature distribution of the simulation model considering the silicone and shell

1.3 硅胶和外壳对结温的影响

热网络模型中的热容在稳态时相当于开路，此时双向Cauer 模型相当于硅胶和外壳的热阻之和（记为R1）与其余7 层结构的热阻之和（记为R2）并联，由于R1远大于R2，双向Cauer 模型的稳态结温与传统模型接近。而当芯片焊料层产生空洞后，R2增加，但R1仍然远大于R2，所以两种模型的稳态结温相差较小。在暂态过程中，由于硅胶的热容值较大，双向模型的结温上升较慢，使结温达到稳态的时间增大。因此，硅胶和外壳对稳态结温影响较小，对暂态结温影响明显。

图7(a)所示是空洞率为15%的模块的两种模型在有限元热仿真中的结温上升过程，在达到稳态时两种模型的结温差仅0.3℃左右，但在暂态过程中，考虑硅胶和外壳的模型的结温上升较慢，两模型的结温差较大。仿真结果与Cauer 模型的分析一致。

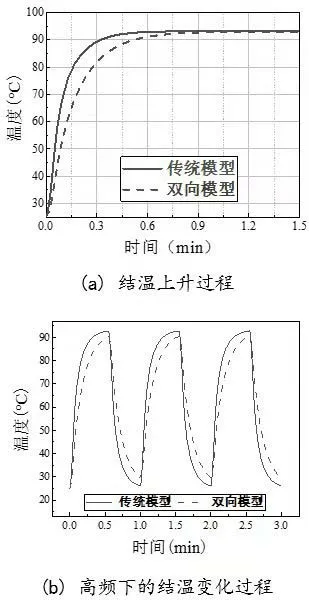
图7 结温变化图Fig.7 Diagram of junction temperature changing

影响IGBT 模块寿命的关键参数除了最大结温外，还有结温波动ΔTj。若模块工作于高频下，芯片导通的时间（即产生功率损耗的时间）小于结温达到稳态所需的时间，此时硅胶和外壳对暂态结温的影响更加明显，甚至会减小达到动态平衡后的结温。图7(b)是高频下，空洞率为15%的模块的两种模型在热仿真中的结温上升过程。在结温达到动态平衡后，单向模型的最大结温为92.735℃，结温波动为66.683℃，而双向模型的最大结温为90.653℃，结温波动为61.335℃。双向热网络模型的最大结温和结温波动均小于单向热网络模型。

硅胶和外壳能有效减小高频下模块的最大结温和温度波动，而在实际应用中，IGBT 模块通常处于高频工况下。因此，硅胶和外壳不仅使芯片温度分布均匀，还提高了模块的可靠性。

2 实验分析与验证

2.1 实验平台

为验证双向Cauer 模型分析的正确性，本文通过实验获取IGBT 模块的结温。采用红外成像仪、热电偶等设备直接测取模块结温时，需要打开模块的封装结构，这种实验方法无法获取完整封装的模块的结温。因此，本文通过热敏电参数与结温的关系推算结温。其中，通态压降Vce是最常用的热敏电参数。

搭建图8 所示的实验平台。在实验过程中将IGBT 模块放置在加热板的中央位置，设置加热板的工作温度为25℃～125℃，步长为25℃，使模块充分受热，此时可以认为加热板的温度与结温Tj相等。设置集电极电流为1A～40A，步长为2A，记录不同集电极电流下Vce的值，获得到不同温度下的I-V 特性曲线。根据I-V 特性曲线拟合得到图9 所示的Tj与Vce和Ic的关系曲面。

图8 实验平台Fig.8 The experiment platform

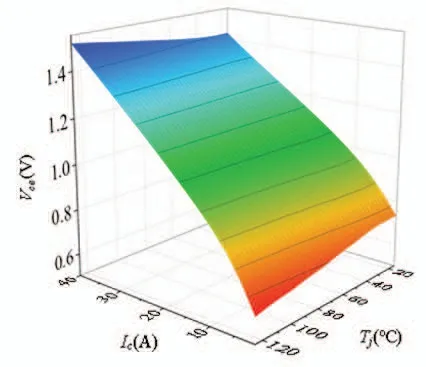
图9 Tj与Vce和Ic的关系曲面Fig.9 The relation surface of Tj to Vce and Ic

2.2 实验结果

通过以上实验步骤，获得健康的模块和空洞率分别为5.5%、9.4%、15%的模块的Tj与Vce和Ic的关系曲面。在室温下，分别给上述模块的集电极通入恒定电流，记录模块达到稳态前不同时刻的通态压降和结温。将通态压降与集电极电流的乘积作为芯片的功率损耗输入热网络模型，通过计算获取模块的结温。图10 为双向Cauer 模型计算的结温与实验测量结温对比，由于空洞率为5.5%的模块的结温与健康模块结温接近，只绘制了健康模块以及空洞率为9.4%、15%的模块的结温曲线。两种方法获得的结果吻合度高，证明双向Cauer 模型的准确性。

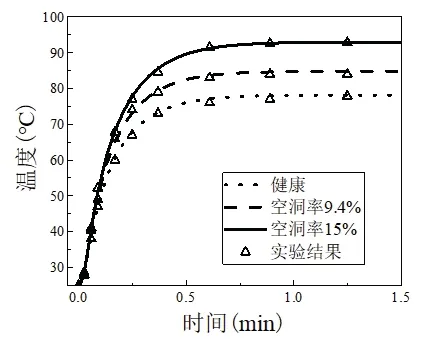
图10 双向Cauer模型计算的结温与实验对比图Fig.10 Junction temperature calculated by bidirectional Cauer model and experimental comparison diagram

3 结论

本文基于IGBT 模块的硅胶和外壳对结温的影响，提出了一种双向热网络模型，解决了当芯片焊料层出现空洞后热网络参数较难确定以及热网络模型计算的结温不准确的问题。通过有限元分析发现，当芯片焊料层出现空洞时，硅胶和外壳可以减小芯片最高温度位置的偏移，降低空洞上方位置的温度，使芯片高温区域周围的温度梯度减小，温度分布更接近健康模型，进而可以简化热网络模型参数的提取。而当模块工作于高频时，硅胶和外壳可降低模块的温度波动，进而减小模块达到动态平衡后的结温，对IGBT 模块起到重要的保护作用。本文通过仿真和实验验证了利用该模型提取IGBT 模块结温的可行性和准确性，有利于电力电子器件可靠性的检测。