起伏地形对三维可控源电磁响应的影响研究

尚晓荣 岳明鑫* 杨晓冬 吴小平 李 勇

(①中国科学技术大学地球和空间科学学院，安徽合肥 230026； ②中国科学技术大学安徽蒙城地球物理国家野外科学观测研究站，安徽蒙城 233500； ③中国地质科学院地球物理地球化学勘查研究所自然资源部地球物理电磁法探测技术重点实验室，河北廊坊 065000)

0 引言

可控源电磁法(Controlled-source electromagnetic method)采用人工场源激发交流电磁波信号(10-3～105Hz)，通过测量目标区交变电磁场达到研究地下介质电性结构的目的。由于成本低、勘探深度大、抗干扰能力强等特点，可控源电磁法在油气和矿产资源勘探[1-2]、地热资源开发[3-4]及环境工程[5-6]等领域发挥了重要作用。可控源电磁法包括时间域电磁法和频率域电磁法。时间域电磁法利用不接地回线源或接地线源向地下发射一次脉冲磁场，在一次场间歇期间，利用线圈或接地电极观测二次涡流场[7-8]。频率域电磁法常见的是可控源音频大地电磁法，主要使用接地水平电偶源作为人工信号发射源[9]，本文研究的即是频率域可控源电磁法。近年来，为适应“深地”国家重大探测战略中电磁精细结构探测的需求，可控源电磁仪器的研发及数据采集技术获得了迅猛发展，数据的反演解释正逐步迈入三维实用化阶段[10-13]。与实际需求相比，三维可控源电磁数据的反演技术尚未成熟，计算效率和准确性均有待提高，特别是考虑起伏地形的三维反演尚不多见[14-15]。正演是反演的基础，反演解释的准确性和计算效率很大程度上依赖于正演算法，因此研究可控源电磁数据的三维高精度正演方法十分必要。

三维可控源电磁法常用的数值模拟方法主要包括积分方程法[16-18]、有限差分法[19-20]、有限体积法[21-22]以及有限单元法[23-26]等。任政勇等[27]基于有限元方法提出一种新的非结构化网格局部节点加密方法，实现了复杂模型完全非结构化四面体全自动剖分； Puzyrev等[28]基于节点有限元方法，采用复杂迭代求解器和基于稀疏近似逆的有效预调节器对大型稀疏线性方程组进行求解，实现了各向异性介质中三维可控源电磁场的正演模拟； 蔡红柱等[29]提出一种基于非结构化网格的海洋电磁有限单元正演算法，该算法适用于井中电磁、航空电磁、环境地球物理等非均匀且各向异性介质的电磁感应基础研究； 汤文武等[30]比较了基于节点有限元与矢量有限元的三维可控源电磁正演，结果表明相同条件下矢量有限元法的计算精度更高，但速度较慢； He等[31]基于棱边有限元方法实现了各向异性介质中三维张量可控源电磁法的正演。

常规可控源电磁数据解释多是基于平坦地形，这会导致反演异常体的位置与形态常发生畸变，甚至产生虚假异常。随着近年来地质勘查目标和野外实地勘测场景越来越复杂，学者们开始研究起伏地形下的三维电磁正、反演。Nam等[32]采用棱边有限元方法研究了大地电磁法在三维地形下的响应特征； Lin等[33]分析了可控源音频大地电磁测深数据的三维地形效应； 殷长春等[34]采用自适应非结构有限元法进行了带地形的时间域海洋电磁法正演。积分方程法、有限差分法和有限体积法大多是基于结构化网格实现的，其中有限单元法对网格剖分比较灵活，非结构化网格更适于模拟真实地形起伏[35]。基于非结构化网格有限元法的二维和三维海洋电磁问题已经取得了一些研究成果[36-38]。相比之下，起伏地形下的陆地三维可控源电磁数值模拟研究相较滞后，目前关于起伏地形对各个场分量的影响特征的研究尚不多见。

因此，本文基于矢量有限元算法开展了起伏地形下的三维可控源电磁法多分量数值模拟研究。采用非结构化四面体网格对计算区域进行剖分，以准确模拟起伏地形，并基于棱边基函数实现电磁场的插值和求解。首先，构建层状介质模型，将其三维矢量有限元计算结果与一维解析解[39]进行对比，验证算法的正确性；其次，构建简单异常体模型，验证算法对探测低阻异常体的有效性； 然后，分别讨论了测点处为山脊地形和山谷地形、发射源处于山脊地形、发射源与测点间为山脊地形等情况下频率域可控源电磁法的响应特征； 最后，研究了复杂三维地质模型的电磁响应特征，验证该算法的实用性。

1 数值模拟理论

从麦克斯韦方程组出发，假设时谐因子为e-iω t的平面电磁波入射到均匀介质中，则计算区域电磁场满足

∇×E=iωμH

(1)

∇×H=σE-iωεE+J

(2)

式中：E为电场强度；H为磁场强度；ω为角频率；μ为介质磁导率；σ为电导率；ε为相对介电常数；J为外加电流密度。

由式(1)和式(2)可得整个计算区域内可控源电磁法满足的电场波动方程

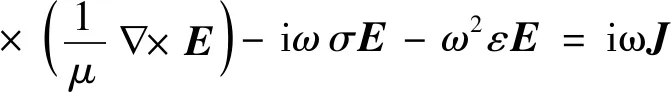
(3)

利用Garlerkin方法，有

(4)

式中：k2=εμω2+iσμω；V表示积分空间。

对式(4)采用基于棱边的非结构四面体矢量有限元法进行求解，电场矢量场可表示为六个矢量棱边插值基函数的线性组合。非结构四面体单元如图1所示。

图1 非结构四面体单元e示意图e1～e6为棱边编号

图1中每一个四面体单元的电场强度可表示为[39]

(5)

由式(4)和式(5)并应用Garlerkin方法，可得电场强度关于单元e的有限元方程

AeEe-iωWeEe-ω2CeEe=iωSe

(6)

式中：Ae、We、Ce是单元e的刚度矩阵；Se为单元e的质量矩阵。矩阵Ae、We、Ce的第(n，j)个元素和矩阵Se的第n个元素可分别表示为

(7)

(8)

(9)

(10)

式中Je为四面体单元e内电偶极子的电流密度。为计算总场方法下的单元源项矩阵Se，将水平线源置于四面体网格的棱边上，假设线源的中点坐标为(x0,y0,z0)，则单元e内的电流密度Je可表示为

Je=Iδ(x-x0)δ(y-y0)δ(z-z0)

(11)

式中：I表示穿过四面体单元的源电流强度； δ为Dirac-δ函数。

对起伏地形模型的正演方程组(式(3))求解时，右端项J不仅包含地下电阻率异常体引起的散射电流密度，还包括起伏地形产生的散射电流密度。使用非结构有限元法剖分模型，同时对地形起伏区域进行网格加密，以更好地对地形进行拟合。

将单元矩阵进行组装，可得到大型稀疏复线性方程组

KE=S

(12)

式中：K=Ae-iωWe-ω2Ce，为正演系数矩阵；S=iωSe，反映源的作用。这里的E即为待求电场强度矢量。通常，K是一大型对称稀疏矩阵，采用CSR(Compressed Sparse Row，稀疏矩阵按行压缩)格式进行存储以减小存储空间。

最后，使用直接求解器Pardiso求解控制方程，可得到单元网格棱边上的电场强度和磁感应强度分量。

2 数值模拟算例

2.1 层状模型

为验证算法的正确性，构建一个三层地层的层状模型。对模型的电、磁响应特征进行分析，并根据模拟结果与一维解析解的相对误差(计算公式为(数值解-解析解)/解析解)分析本文算法的精度。

层状模型的空间尺寸为100km×100km×100km，如图2a所示。发射源位于y=-10km处，测点位于原点，发射频率为0.1～5000Hz，共10个频点：0.1、0.5、1、5、10、50、100、500、1000、5000Hz。用非结构四面体网格剖分生成的最终网格分布见图2b。采用Key[40]提出的一维可控源电磁正演算法与本文基于非结构矢量有限元算法进行模拟，并对比响应曲线，结果见图3。由图可见，本文算法模拟结果与一维解析解吻合较好，电场的分量Ex实部和虚部的数值解与解析解的相对误差的绝对值分别小于1%和2%，精度较高，验证了本文算法的正确性。

图2 层状模型几何结构(a)和网格剖分示意图(b)

图3 层状模型Ex分量实部和虚部数值解与解析解对比(左)及其相对误差(右)

在保证精度的前提下，分别测试了层状地层模型不同剖分网格单元数情况下数值模拟所需要的时间，并统计了数值解与解析解的误差，结果见表1。

从表1可以看出，网格数增加约1倍时，数值模拟耗时大约增加2倍； 网格数大于33万后，误差下降较慢。因此，在综合考虑耗时与精度的情况下，本文选择33万网格数进行后文模型剖分。

表1 层状模型数值模拟时间和精度统计

2.2 简单组合异常体模型

为了分析本文算法对异常体电阻率的敏感性，构建两组简单组合异常体模型，背景为均匀半空间。模型包含4个相同的低阻(10Ω·m)/高阻(1000Ω·m)异常体，异常体尺寸为500m×500m×200m(图4)。模型空间为100km×100km×100km； 发射源点位于y=-3km处； 测量点位于x轴的-1～1km、y轴-1～1km所围区域的地面，x、y方向的点距均为200m； 发射频率同前文层状模型。对接收点附近进行了网格加密，在远离观测点处，网格剖分比较稀疏，模型最终网格剖分如图5所示。

图4 简单组合异常体模型

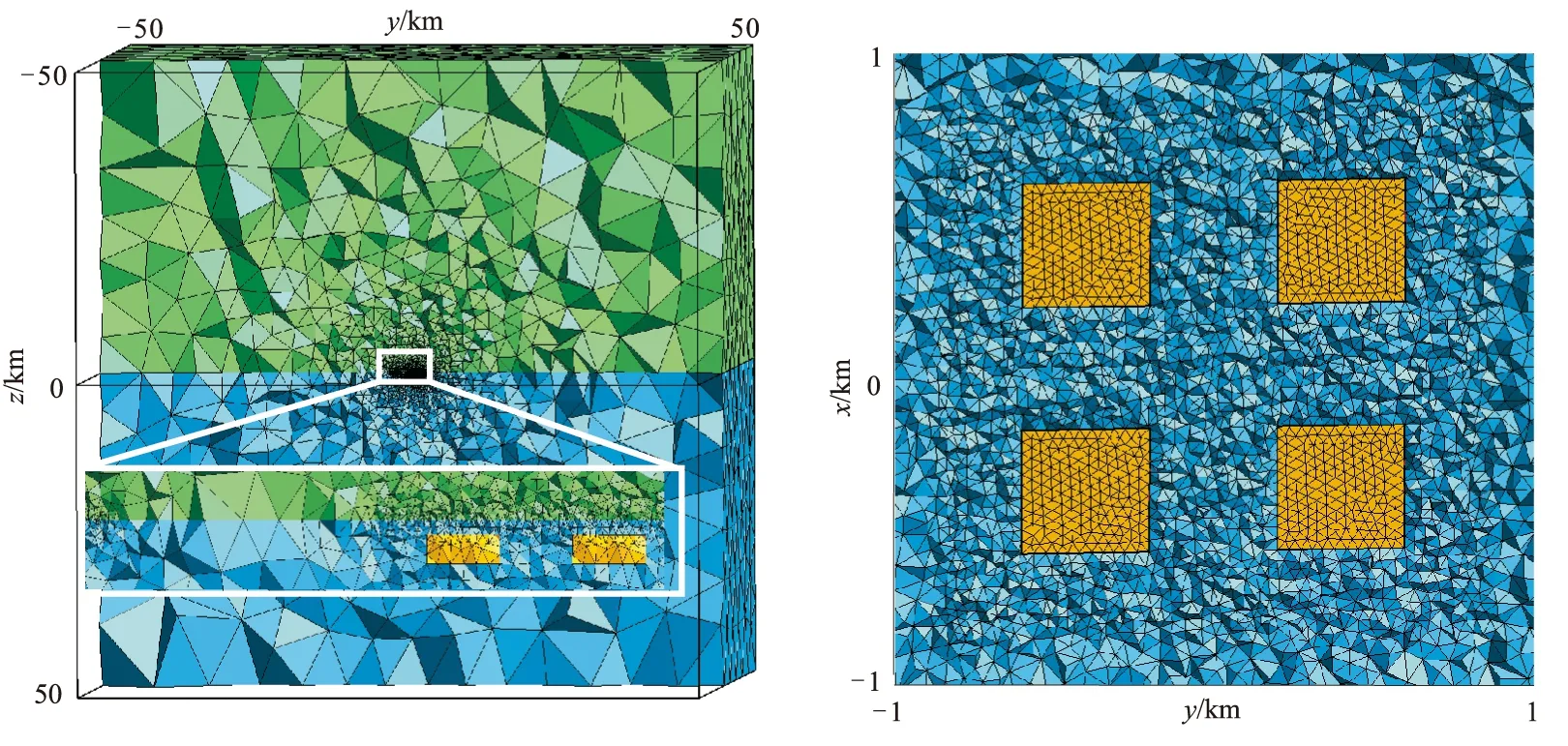
图5 组合异常体模型网格剖分示意图左：x=0剖面； 右：z=100m剖面。黄色方块是异常体

分别对低阻异常体和高阻异常体两个模型进行模拟，结果见图6。从图中可以看出，低阻异常体产生的电场强度异常较高阻异常体明显，且不同频率时的相对异常(绝对值)也不同。

图6 简单组合异常体模型的Ex振幅曲线(左)及其相对异常曲线(右)

为了进一步分析背景模型、包含高阻异常体和低阻异常体模型的电场特征，绘制了0.5Hz的Ex振幅图(图7)。可以看出，异常体的赋存区域在有、无异常体的情况下差异较大； 对比低阻和高阻异常体的情况可知，频率域可控源电磁法对于低阻异常体更敏感。

图7 0.5Hz时组合异常体模型地表Ex分量振幅图(a)不存在异常体(背景模型)； (b)存在低阻异常体； (c)存在高阻异常体； (d)图b与图a的相对异常； (e)图c与图a的相对异常

2.3 三维起伏地形模型

2.3.1 测点处山脊地形模型

建立一个含有山脊地形的三维简单异常体模型(图8)。山脊顶部长、宽均为800m，底部长、宽均为1600m，高度为400m，其中心点位于(0，0，200m)。假设大地背景电阻率为100Ω·m，异常体为不规则形状(图8中的蓝色区域)，厚度为200m，长、宽均为500m，电阻率为1Ω·m，中心点位于(0，0，750m)。采用非结构化四面体单元对模型进行网格剖分，对发射源和接收点处进行网格加密，模型网格剖分结果见图8。采用线源，源中点水平位置为(3km，-3km)，发射频率同前文层状模型采用的频点； 接收点位于地面-1～1km(x)、-1～1km(y)区域内，x、y方向测点间距均为200m。

图9为图8所示三个模型在测点(0，0，0)处的电场强度分量(Ex)和磁感应强度分量(By)振幅计算结果。由图可见，模型M02与模型M03的正演Ex和By振幅曲线较一致，而M01模型与二者相差较大，说明山脊地形会削弱异常体的存在，同时也说明正演时如果忽略山脊地形，会对正演结果产生较大影响。对比图9b与图9d可以发现，山脊地形对Ex振幅的影响大于对By振幅的影响。

图8 山脊地形低阻异常体模型网格剖分示意图(a)水平地形的低阻异常体模型(M01)； (b)含山脊地形的低阻异常体模型(M02)； (c)含山脊地形的无异常体模型(M03)

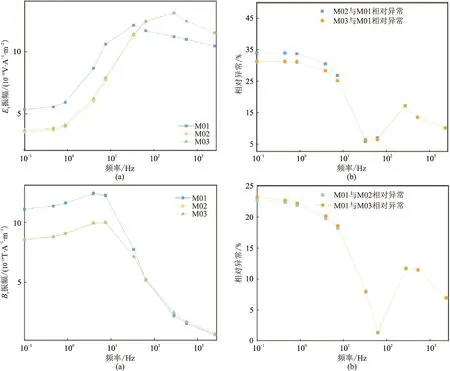
图9 山脊地形模型Ex和By振幅正演曲线及相对异常(a)Ex振幅； (b)Ex振幅相对异常； (c)By振幅;(d)By振幅相对异常

图10为图8中三个模型在频率为1Hz时沿x方向(y=0)的正演分量Ex和By的振幅及其相对异常。可以看出，山脊根部位置的正演Ex和By振幅均高于水平地形下的场分量幅值，山脊顶部位置的正演Ex和By振幅均低于水平地形下的场分量幅值，这是由于在地形高处(即山脊顶部)，供电电流是发散的，会呈现低电流密度，而在地形相对低处(即山脊根部)，供电电流是收敛的，呈现高电流密度。此现象说明山脊地形会削弱异常体所产生的异常。

图10 1Hz时山脊地形模型Ex和By振幅曲线(a)Ex振幅； (b)Ex振幅相对异常； (c)By振幅;(d)By振幅相对异常

2.3.2 测点处山谷地形模型

建立一个含有山谷地形的简单低阻异常体模型(图11)。山谷顶部长、宽均为1600m，底部长、宽均为800m，高度为400m，其中心点位于(0，0，200m)。异常体参数与前文的山脊模型低阻体相同。采用与山脊地形模型相同的加密剖分网格，在相同位置布设发射源、接收点，采用同样的发射频率。模型网格剖分结果见图11。

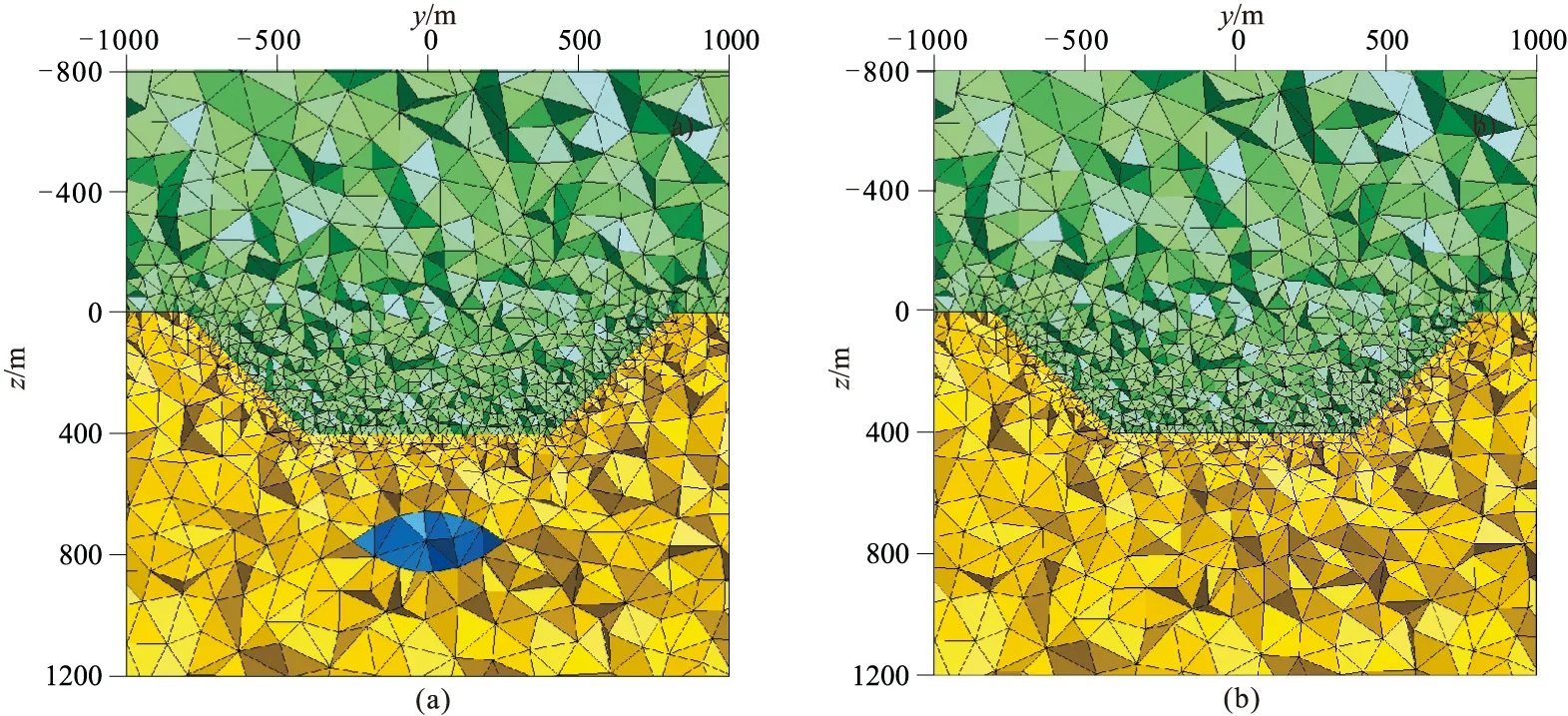
图11 山谷地形模型网格剖分示意图(a)低阻异常体模型(M04)； (b)无异常体模型(M05)

图12为水平地形的低阻异常体模型(M01)和图11中的山谷地形模型M04和M05的Ex和By正演振幅曲线及相对异常曲线。由图可见，M01、M04和M05三个模型的电、磁场强度振幅曲线差异较大； 与山脊地形的By正演振幅曲线(图9c和图9d)相比，山谷地形低阻体模型的差异更大，可见频率域可控源电磁法的电场强度、磁感应强度分量受山谷地形的影响更大。

图12 山谷地形模型Ex和By振幅正演曲线及相对异常(a)Ex振幅； (b)Ex分量振幅相对异常； (c)By振幅; (d)By振幅相对异常

图13为山谷模型在频率为1Hz时沿x方向(y=0)的正演Ex和By振幅及振幅相对异常。可以看出，在山谷两侧Ex和By振幅均低于水平地形下的场分量幅值，在山谷底部则均相反。这一特征与山脊地形的计算结果相似，这是由于在地形高处，地表下供电电流发散，呈现低电流密度； 在地形相对低处(即山谷底部)，供电电流收敛，呈现高电流密度。此现象说明山谷地形会增强异常体产生的异常。

图13 1Hz时山谷地形模型Ex和By振幅沿x方向变化曲线(a)Ex振幅； (b)Ex振幅相对异常； (c)By振幅; (d)By振幅相对异常

2.3.3 发射源处起伏地形模型

构建一个发射源处为起伏地形的模型(图14)。源的中点位于起伏地形区域的中心位置(0，-8000m，-395m)，山脊顶部长、宽均为1000m，底部长、宽均为1600m，高度为400m。其他参数设置均与测点处山脊地形模型参数相同。发射源处地形平坦模型(M06)和地形起伏模型(M07)的网格剖分结果见图14。

图14 发射源处地形平坦模型(M06，上)和地形起伏模型(M07，下)网格剖分示意图

图15为模型M06和M07在测点(0，0，0)处的电、磁场分量Ex和By振幅随频率变化曲线及相对异常。从图15a可以看出，频率高于100Hz时，模型M07的Ex振幅高于模型M06； 频率低于100Hz时，情况相反。这是因为频率越低，探测深度越大，发射源处的地形为山脊地形，相对增加了介质厚度； 而且，对于高阻异常体，在相同的频率下，电场衰减较快，振幅衰减也更快。高频信号的探测深度较小，发射源处向下传导的电流在相同深度接收点处的电场信号强度会更大。另外，从图15b可以看出，两个模型的Ex相对振幅差较大，最大值达48%。由图15b和图15d可见两个模型的By分量相对异常与Ex分量有相似特征。

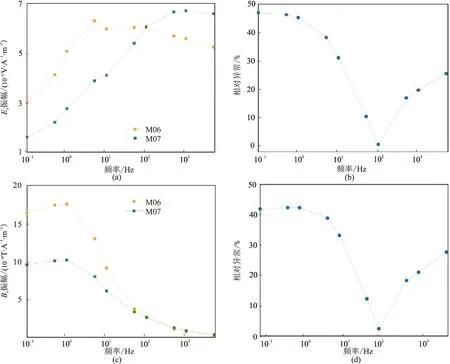
图15 发射源处地形起伏模型Ex和By振幅正演曲线及相对异常(a)Ex振幅； (b)Ex分量振幅相对异常； (c)By振幅; (d)By振幅相对异常

2.3.4 发射源与测点间地形起伏模型

建立一个源点与测点间地形起伏模型(图16)，分析这类地形对可控源电、磁场响应的影响特征。起伏地形山脊顶部长、宽均为800m，底部长、宽均为1600m，高度为400m，中心点为(0，-2000m，0)。发射源中点位于地表(8km，-8km)处。其他参数设置同2.3.1节模型。图16为发射源和测点间地形平坦模型(M06)和地形起伏模型(M08)网格剖分图。

图16 发射源与测点间地形平坦模型(M06，上)和地形起伏模(M08，下)网格剖分示意图

图17为模型M06和M08在测点(0，0，0)处的电、磁场分量Ex和By振幅曲线及振幅相对异常曲线。从图17a和图17b可见，两个模型的Ex振幅较接近，差异较小。另外，发射源与起伏地形的距离、地形起伏程度、地形与异常体的距离等因素也会影响电、磁场。图17c和图17d是两个模型By分量振幅曲线和相对异常曲线，可见By分量振幅相对异常曲线与Ex分量有相似规律。

图17 发射源与测点间地形起伏模型Ex和By振幅正演曲线及相对异常(a)Ex振幅； (b)Ex分量振幅相对异常； (c)By振幅; (d)By振幅相对异常

从上述分析可知，由于地形的存在，尤其是发射源之下起伏地形和测点处的起伏地形，采用频率域可控源电磁法对地下异常体进行探测时，电、磁场分量均发生了畸变，出现了虚假异常。因此在实际数据的处理解释中，需要考虑地表地形对可控源电磁法电、磁场的影响。

3 复杂金属矿应用实例

为了验证本文算法在实际应用中的可靠性，以湘西某铜铅锌多金属矿床的成矿模式为基础建立图18所示地质模型，所包含的主要岩(矿)石的电阻率信息如表2所示。

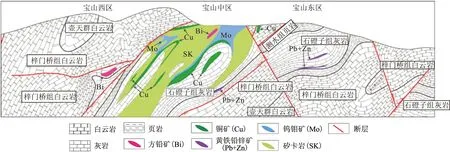
图18 湘西铜铅锌多金属矿床成矿模式图

表2 湘西铜铅锌多金属矿床主要岩(矿)石电阻率统计

根据表中岩(矿)石电阻率范围，取其平均值，给出图19所示的金属矿床模型二维电阻率填图结果及其非结构四面体模型网格剖分结果。对原模型四周区域进行延拓，其中空—地边界沿原模型边界两端分别向两侧延伸，而延拓区域的地层电阻率设为与原模型相邻区域的电阻率一致。延拓模型空间范围为40km×40km×40km，包含四个长度为1km的线源，发射电流为1A，源的中点坐标分别为(0，-3000m，105m)、(-3000m，0，115m)、(0，3000m，162m)和(3000m，0，115m)(图20)。模型中异常体分布区域为-750m≤x≤750m，-750m≤y≤750m，0≤z≤400m，低阻目标体为图19中填图颜色为蓝紫色的小规模片状块体及青绿色的块状异常体。测点沿地形起伏均匀分布，地表范围为-750m≤x≤750m，-750≤y≤750m，测点间距为100m。发射频率为0.1～5000Hz，频点分布同2.1节层状模型。

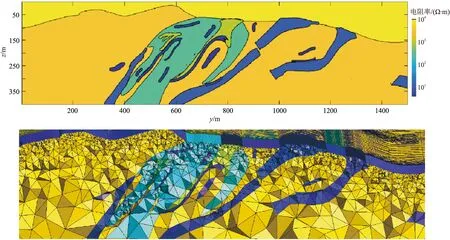
图19 湘西铜铅锌多金属矿床模型二维电阻率填图(上)及其非结构四面体单元剖分局部示意图(下)

图20 湘西铜铅锌多金属矿床延拓模型发射源布置示意图

分别正演计算有、无异常体情况下，金属矿床模型中心点在x=0、y=-200m处Ex振幅随频率的变化曲线，结果见图21a，二者的相对异常见图21b。由于模型深部电阻率均一，因此低频时Ex振幅较稳定，且相对异常基本保持为常数； 在高频段，由于地质异常体分布复杂，图21b中的相对异常曲线出现了明显的波动。

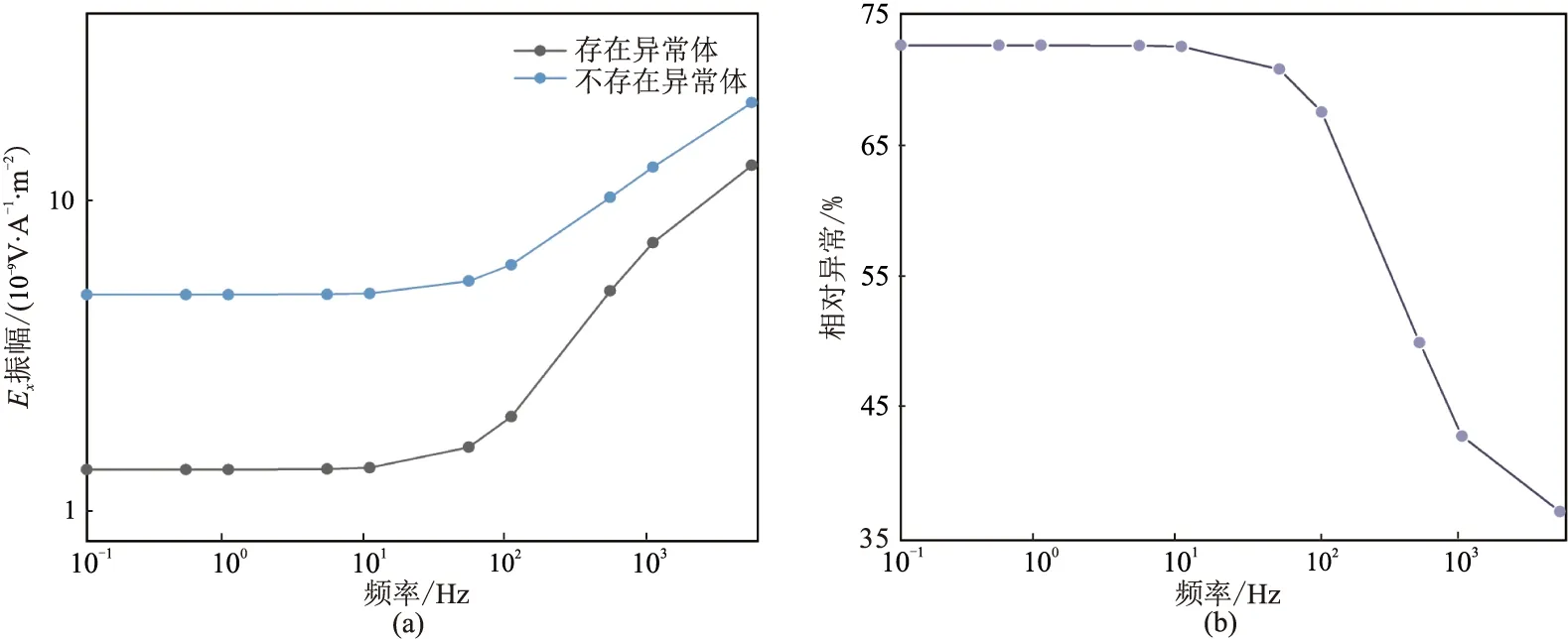
图21 金属矿模型偏移距x=0、y=-200m处Ex振幅随频率变化曲线(a)及相对异常曲线(b)

选取正演计算的频率1Hz时的Ex和By振幅数据，绘制图22所示的等值线图。可以发现，Ex和By振幅异常区域均与低阻地层的平面位置大致吻合(图22中虚线椭圆区域)； 同时，Ex和By振幅相对异常图中相对异常较大的区域(图22中实线椭圆区域)也与实际低阻异常体的赋存区域存在很强的相关性。

图22 金属矿模型频率1Hz时正演计算的地表位置Ex(上)和By(下)振幅等值线图及相对异常图(a)包含异常体； (b)不包含异常体； (c)图b与图a的相对异常

4 结论

本文基于非结构四面体网格和矢量有限元法实现面向复杂地质模型的可控源电磁法三维多分量数值模拟。通过对比层状模型的数值解与一维解析解，以及组合异常体模型的电、磁场强度响应特征分析，验证了本文算法的正确性和有效性，说明了模型剖分方案的合理性。通过测点处山脊和山谷地形模型、发射源下山脊地形模型、发射源和测点间山脊地形模型的数值模拟，说明了地形起伏对可控源电、磁场会产生显著的影响。因此，在地形复杂的区域开展可控源电磁工作必须考虑地形的影响。实际复杂带地形金属矿模型的计算结果也进一步验证了该算法的实用性和可靠性。