销售排名、电商数量与价格离散
2022-02-18李秀敏
张 艺,李秀敏
(广东工业大学经济与贸易学院,广东广州 510520)
一、引言
自网络经济诞生以来,人们对互联网销售的低搜索成本寄予厚望,价格比较网站的出现使跨平台搜索商品的成本大大降低。经济学一般原理认为,只要电商数量足够多,线上销售市场可能接近于理论上的完全竞争市场结构,厂商将失去定价权,相同商品的价格将完全统一,不可能存在价格离散。已有研究发现,线上商品的价格决定既受商品提供方特征和购买者决策过程的影响,也受网络销售平台排名规则的影响[1-2]。国外研究发现[3],价格比较网站可以通过对价格和销量的排名,让消费者获取价格的全部信息,从而降低信息搜索成本,使得价格离散程度下降。遗憾的是,目前国内这方面的研究还鲜有出现。
研究电商平台与价格的关系对促进我国经济发展有特殊的意义。我国经济发展要立足国内循环,深挖内需潜力,促进形成强大的国内消费市场对经济增长的基础性作用。根据商务部2021年8月11日发布的《2021年上半年中国网络零售市场发展报告》,我国互联网销售平台消费的迅猛发展已成为引领国内大循环的重要动力,仅2021年上半年,网上零售额达6.11 万亿元,同比增长23.2%。同时,互联网销售平台的电商竞争愈演愈烈,网上零售额增长伴随着电商数量的缩减,2021年6月底网络零售平台商铺数量为2 152.5 万家,同比下降6.9%,大网络销售平台的垄断地位得到进一步巩固。①
对于价格离散产生原因的解释,经典的微观经济学理论认为,厂商数量越多,厂商对价格的影响越小。在完全竞争市场情况下,市场上存在无数的厂商,市场价格是统一的,不存在价格离散的现象,这被称为“一价定理”。但是,信息经济学理论的开创者斯蒂格勒(Stigler)[4]认为,当厂商数量增加时,消费者如果要找到最有利的价格,需要检索所有的价格,这需要花费信息搜寻成本。即使是完全相同的商品,也存在价格离散。零售电商的重要特征是信息搜寻成本比传统零售要低,消费者获取信息的搜寻成本越来越低,但线上商品的价格离散现象却没有消失。所以无论是经典的市场结构理论还是信息搜寻理论,都无法完全解释互联网销售平台上价格离散依然存在的问题。而且当电商数量增多、竞争加剧时,是否会降低价格离散程度仍有待探讨。
20世纪90年代开始,许多学者利用网上销售数据对电商数量和价格离散关系展开实证研究,这些研究集中在以美国为代表的电子商务起步较早的国家,他们发现价格离散程度在互联网销售平台上并不比传统线下销售渠道低[5-9]。国内关于价格离散的研究出现在2000年以后,涌现了许多围绕互联网平台价格离散的实证研究[10-14]。但已有研究的结论依然存在较大分歧,对电商数量影响价格的机制还不清楚。尤其是价格比较网站出现后,国内还没有研究价格比较网站影响价格离散的文献。从数据上来看,已有对价格离散的研究数据主要来自以淘宝、京东为代表的少数互联网平台[13,15],未见基于全网电商数量与价格离散的研究。实际上,消费者搜寻的范围不仅仅在某一个平台,而是跨平台,市场的边界不应局限于某个电商平台,价格比较网站的出现降低了消费者跨平台搜寻商品的成本。因此,本研究利用价格比较网站上对商品销售排名的数据考察全网电商数量对价格离散影响。
二、文献综述与理论模型
(一)文献综述
市场结构决定价格离散的程度,垄断电商可以通过价格歧视实现对不同消费者采取不同的价格,垄断市场上价格的离散程度更高。相反,完全竞争市场中的众多电商是价格接受者,厂商无法进行价格歧视,价格不存在离散的现象。所以,理论上,电商数量越多,厂商实施价格歧视的能力越弱,价格离散程度越低。但为什么现实中电商数量增多,价格离散度并没有减少?经典的价格离散理论认为,价格离散是由搜寻成本导致的。但随着零售电商的发展,消费者在线上购物时搜寻成本被大大降低,而价格离散并没有消失,经典的搜寻理论无法完全解释价格离散的现象。已有文献对在线商品的价格离散现象进行了广泛的研究,本文通过梳理国内外文献,重点阐述已有文献对价格离散的解释及其不足。
已有研究发现,由于信息不对称,消费者对商品的价格无法完全了解,获取价格信息需要成本,这种类型的信息成本被称为搜寻成本。搜寻成本是造成价格离散的主要原因,有学者建立了搜寻成本模型,斯蒂格勒[4]于1961年在该领域做出了开拓性的贡献。卡普兰(Kaplan)等[7]的研究发现,价格离散程度30%以上可以由搜寻成本解释。更低的搜寻成本意味着消费者可以更容易发现和比较不同的价格,确定同一商品不同价格的最低价,减少价格歧视,降低价格的离散程度。在网络交易平台上,搜寻成本被降低了很多,甚至被认为接近于零,称为点击成本(Cost of Click)。信息交流技术(Information and Communication Tech⁃nology,ICT)的发展使微观搜寻成本下降,并影响宏观的经济周期。搜寻成本的下降会对不同市场价格如金融市场的利率、劳动力市场的工资、零售市场的价格等有不同的影响[9]。线上零售的价格并没有比线下价格的离散程度更低。许多类似的研究都证实在线商品的价格存在巨大并且稳定的价格离散程度[16]。
对此,搜寻成本理论认为,消费者在网上搜寻商品时,可以获取的商品信息是多维度的,包括价格、质量、信誉、运费、到达时间、售后服务等。搜寻成本并不是绝对的外生变量,而是电商可以操控的内生变量。事实上,研究发现,与实体店中搜寻商品品牌的行为相比,消费者在线上商店中搜寻商品品牌的成本更大,而且,线上广告对消费者线上搜寻的行为影响很大[17]。
有部分研究将网络销售过程看成信息交换的过程,以信息交换所理论解释价格离散的现象。消费者通过咨询信息交换所(指互联网不同价格比较网站)获取价格信息[8]。信息交换所的显著特点是,一部分消费者可以通过信息交换所获得所有商品的价格列表,并以最低的价格购买。在最早的模型中,均衡价格差异源于消费者或厂商的事前异质性,也被称为厂商异质性模型。早期的模型将厂商进入信息交换所的决策视为外生,新信息交换所模型则放松了这一假设,将厂商和消费者进入信息交换所的决策视为内生,且信息交换所向访问或传输价格信息的消费者和厂商收取的费用也是内生的[18]。信息交换所理论表明,即使在消费者或消费者群体没有任何事前异质性的情况下,只要存在价格的信息交换所,就会存在离散价格的市场均衡。但是,信息交换所理论还不能完全解释价格比较网站对商品价格离散的影响。价格比较网站可以跨越多个平台进行信息搜索,因此其对价格离散的影响范围不应局限于单一的交易平台。
搜寻成本理论与信息交换所理论都忽略了决策者的有限理性,而有限理性会影响消费者对价格的选择。有限理性理论放松了纳什均衡模型中的完全理性假设,即每个决策者选择一个行动(无论是价格还是搜寻策略),都是对其他市场参与者既定行动的最佳反应。有限理性理论认为决策者是有限理性的,有限理性下价格离散分布的均衡状态分别是定量反应均衡(Quantal Response Equi⁃librium,QRE)[19]和ε 均衡[20]。在QRE 均衡中,离散的均衡价格分布源于厂商的有限理性。这种有限理性可能源于管理者认知处理能力的限制或互联网零售商使用的动态定价算法。在ε均衡中,价格离散分布可能是由电商认知或动机限制产生的。有限理性理论弥补了搜寻成本和信息交换理论的不足,但其不足之处是对消费者有限理性行为的解释能力较差。
从已有文献看,现有理论从不同角度解释电商销售商品存在的价格差异,价格离散程度由所有市场参与者的相互作用决定。搜寻成本、电商和消费者的有限理性以及信息交换成本都会影响价格离散程度。事实上,并不存在解释价格离散的最优模型,不同模型适用于分析不同的市场环境。例如,搜寻成本理论适合分析消费者必须访问不同商店或网站以收集价格信息的情况。而当消费者能够访问价格比较网站时,应该考虑信息交换所模型对商品排名所产生的搜寻成本对价格的影响。
根据相关理论,如果存在搜寻成本,则电商数量越多,消费者需要通过不断的搜寻才能寻找到最低价,搜寻成本的存在会导致价格差异,这可以部分解释价格离散的现象。价格比较网站可大大降低消费者的搜寻成本,它相当于价格的信息交换所,通过对全网所有平台上同样商品的销售排名,帮助消费者迅速了解所有商品信息,实现跨平台的商品搜索。因此,需要考虑构造一个同时基于搜寻成本和信息交换所的理论分析框架,从理论上加深对价格离散问题的理解。
(二)分析框架与研究假设
理论分析框架的核心假设是搜寻成本由哪些因素决定,这需要审视搜寻成本理论的相关假设。第一,传统的搜寻成本理论将搜寻成本视为外生变量,但线上商品的搜寻成本实际上是由电商平台控制的,电商数量越多,搜索到合意的商品就越困难,因此搜寻成本是内生变量,并且电商的数量越多,竞争越激烈,消费者的搜寻成本就越高。第二,消费者在搜寻商品过程中的有限理性也会影响其商品选择行为。消费者的搜寻过程并不完全遵循理论模型所假设的完全理性。即使是完全同质的商品,消费者对商品的选择可能会考虑许多因素,如配送速度、是否包含邮费、电商所在城市以及电商的信誉等,所以不存在完全的理性抉择,消费者付出的搜寻成本越来越高,存在着边际搜寻成本递增的规律。第三,根据信息交换所理论,电商在网络平台的竞争存在进入门槛,价格比较网站会发挥类似于信息交换所的作用,通过销量排名的方式,使一部分电商的产品被消费者优先搜寻到。因此排名越前,消费者的搜寻效率越高。以上假设说明,电商数量越多,搜寻成本的边际递增和销量排名都会影响商品的搜寻成本,导致价格出现离散状态下的市场均衡。基于此,我们借鉴王强和陈宏民的研究[21-22],构建如下理论模型。
假设全网线上交易市场上存在N 个电商,他们销售成本为pc的同质商品,按照综合受欢迎程度如销量、好评率、价格等因素排序,将所有电商分成高声誉和低声誉两种,其概率分别是β 和1-β 。消费者在搜寻某种商品时,购买高声誉和低声誉电商商品的概率分别为qH与qL,高声誉和低声誉电商的定价分别为pH和pL。假设在网络平台上销售,需要缴纳一定的费用e,则电商总的成本为C=pc+e。
假设市场中存在大量消费者,依据其对某种商品的保留价格分为高保留价格ph和低保留价格pl两种类型,且ph>pl>pc,两种消费者所占的比例分别为λ 和1-λ。消费者在搜寻电商的商品时所需要的搜寻成本为Nms2,其中,N 为全网所有电商的数量,m 为价格比较网站的销量排名,排名越靠前的商品,被搜寻到的概率越高,搜索效率越高。也就是说,m 越小,排名越靠前,搜寻效率越高,所需要的搜寻成本越低。s 为搜寻活动所能提高的找到目标商品的概率,这里采用平方的形式是因为搜寻成本存在边际成本递增的规律[12]。
假设消费者和电商都是风险中性,消费者购买商品所获得的效用为保留价格与销售价格之差。如果消费者不进行搜寻活动,在电商中随机选择进行交易,没有搜寻成本,那么高保留价格和低保留价格的消费者效用分别为:
Uh=β(ph-pH)+(1-β)(ph-pL)
Ul=β(pl-pH)+(1-β)(pl-pL)
如果消费者付出一定的搜寻成本,可以将找到高声誉电商的概率从β 提高到β+s,相应地,找到低声誉电商的概率从1-β 降低到1-β-s,搜寻活动需要付出的成本为Nms2。
对于消费者而言,高保留价格消费者的最优搜寻活动sh,最大化其效用函数如下:
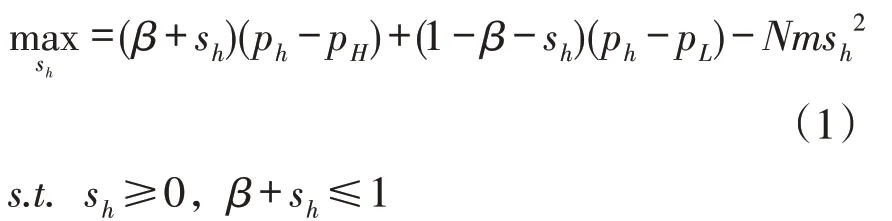
同样,低保留价格消费者的最优搜寻活动sl,以最大化其效用函数:
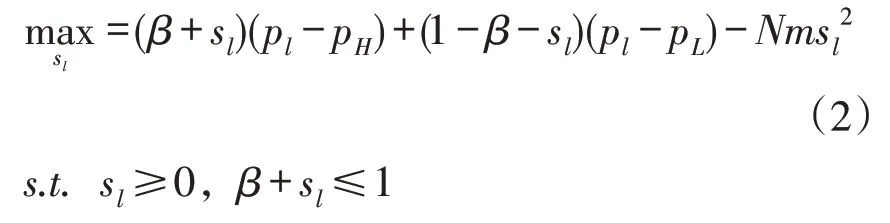
根据式(1)和式(2),分别对其求一阶导数,并在等于零点处取得极值,可以解出高保留价格和低保留价格消费者的最优搜寻活动为:

将式(3)代入搜寻成本的表达式中,可以解出,搜寻成本等于
对于电商定价的决策考察,可以假设电商的定价行为遵循追求利润最大化的原则。对于高声誉电商的利润最大化目标函数为:
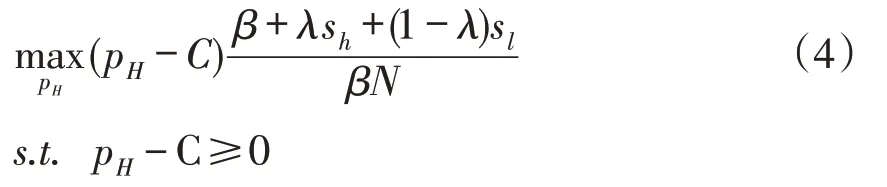
式(4)中sh、sl分别为高保留和低保留价格消费者的搜寻活动可以提高搜寻目标商品的概率。同理,低声誉电商的利润最大化目标函数为:
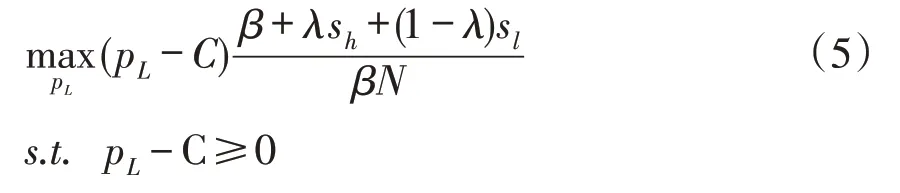
将式(3)中搜索活动的表达式代入到式(4)和式(5)中,然后,对其求一阶导数,并在取零值处解出pH和pL的价格差表达式。
pL-pH=Nm
该表达式说明,价格离散程度与厂商数量成正比,与销量排名成正比。由此提出以下两个研究假设:
H1:电商总数量越多,搜寻成本越高,价格离散程度越高。
H2:价格比较网站上销量排名越靠后,搜索效率越低,搜寻成本越高,价格离散程度越高。
三、模型构建与数据来源
(一)模型构建
为检验研究假设H1,参考姜永玲等[13]的做法,本研究构建双向固定效应模型,用于检验电商数量对价格离散程度的影响。由于无法完全控制所有影响商品价格的因素,本研究采用双向固定效应模型来解决遗漏部分影响商品价格变量所导致的估计偏误问题。通过加入商品的个体固定效应和商品销售的时间固定效应,可以观察同种商品在不同时期的价格变化,从而控制不随时间变化的商品属性因素对价格产生的影响。
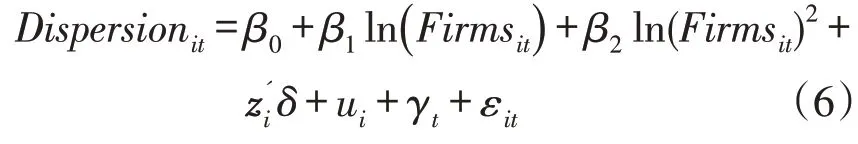
其中i=1,...,n;t=1,...,T。
在式(6)中,Dispersionit表示商品i 在日期t的全网电商中的价格离散度。对核心解释变量全网电商数量Firmit取对数处理,并分别加入电商数量一次项和二次项,以检验假设中电商数量与价格的非线性关系。是虚拟变量,用于表示商品的特征,包括品牌、商品类别等。δ 是虚拟变量的系数。为控制不可观测的影响价格的商品特征,在模型加入商品固定效应ui和时间固定效应γt,前者可以剔除不随时间改变的遗漏变量带来的估计偏误,后者可以剔除不随商品改变的时间趋势带来的估计偏误。当无法完全控制影响商品价格的所有特有属性如配置、性能、外观、设计、品牌忠诚度等,以及不同时间段的全网统一的促销活动对价格的影响,控制商品固定效应和时间固定效应可以有效避免遗漏变量偏差,减小内生性来源。在模型(6)中,核心解释变量Firmit的系数β1衡量电商数量对价格的影响,用于检验假设H1是否成立。
对于随机误差项εit的处理,考虑到不同商品的价格波动幅度不同会导致异方差的问题,并且由于数据样本来自面板数据,同一商品在不同时间的价格水平间存在相关性,为同时解决不同商品间存在的异方差以及同一商品在不同时间的自相关问题,我们将标准误聚类到商品层面,εit为聚类稳健误差项。
为检验假设H2,在模型(6)的基础上,将样本按价格比较网站上的销量排名前10位分成10类,分别依据模型(6)做分样本的双向固定效应模型10 次回归,以检验商品在不同销量排名的位置是否影响价格离散度。
(二)数据来源
本研究的数据来自国内知名的价格比较网站“慢慢买”的销售排名,该比价网站是国内有影响的专业比价网站,汇集了所有主流网上商城的商品报价、活动促销、历史价格走势等信息。该网站价格监测系统积累了国内50 余家主流电商平台、超万家品牌、1 000多万种商品价格、销售、店铺、品牌等相关应用数据,基本覆盖了国内所有电商平台的主要销售数据。本研究2020年8月20日至11月22日每3天收集1次数据,共35期约3个月的商品销售数据,构成由商品名称和销售日期两个维度所组成的面板数据。总共包含170大类商品,542种商品品牌,3 615种不同商品,共35 153个样本。
本研究数据收集的时间覆盖了“双11”线上购物季,促销活动较多,可以观察同种商品较大幅度的价格变化。这一时间段的价格波动基本与商品本身的属性无关,而与电商数量及电商之间的竞争策略有关,可以视为外生冲击造成的结果。因此,该阶段数据特有的属性可以很好地解释电商数量与价格之间的关系。
目前没有统一的被解释变量价格离散度的计算方式,主要采用以下几种指标:最高价与最低价之间的差;价格的方差或标准差;平均价格和最低价格之差;使用价格的变异系数。以上4种指标各有优劣,考虑到数据可得性,本研究采用第三种做法,用平均价格与最低价格的差额反映价格的绝对变化幅度。但由于不同商品价格的数值相差较大,为减少价格绝对数值的影响,采用类似于变异系数的构建方法,参考姜永玲等[13]的离散指标构建方式,将上述差额除以平均价格。具体计算方式:价格离散度=(商品平均价-商品最低价)/商品平均价。
核心解释变量电商总数采用比价网上爬取的全网电商总数,为减小离群值的影响,参考已有研究对离群值的常见处理方法[23],本研究将离群值最高部分的1%进行截尾处理。需要说明的是,本研究将全网电商数量作为核心变量,主要是因为消费者在网上消费时往往进行跨平台搜寻。本研究主要关注的是市场结构与电商数量的关系,全网的电商数量可以刻画不同的市场结构。随着互联网技术的发展,网络搜寻成本越来越低,电商间的竞争不仅仅局限于某个平台内部,而是所有的网络平台。商品最低价和平均价为相同商品在所有电商价格的最低值与平均值。
(三)描述性统计
为验证本研究使用的价格比较网站数据是否存在严重的样本选择性偏误,即价格和电商数量是否受到操控,我们绘制了价格离散的概率密度图(参见图1)。从成本上考虑,厂商对商品定价时存在最低价,但对最高价一般不存在上限。所以,价格离散分布应该存在一个长尾。从图1可以看出,价格离散分布是长尾分布,说明我们所使用的样本数据与理论上对价格离散分布的预期相吻合。
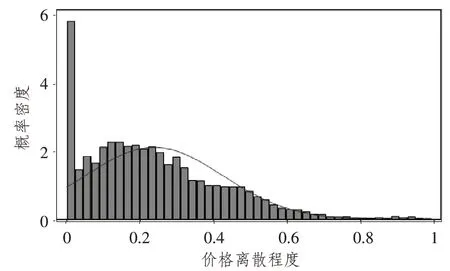
图1 价格离散的概率密度
本研究所使用变量的描述性统计见表1,可以看出价格离散度变化从0 到0.994,平均值为0.237,说明价格平均值与最低值之间的价格差占平均价格的23.7%。商品的平均价和最低价的变化幅度都很大,如平均价的范围是8.9 元至46 800元,最低价的范围是5.5 元到39 800 元,这与商品的种类有关,不同商品的价格相差悬殊。核心解释变量电商数量从只存在1 家电商的绝对垄断市场到接近于完全竞争市场的9 205家电商,平均电商数为66 家。样本包含了3 615 种商品、170 种商品大类和542 种商品品牌。数据覆盖的日期为2020年8月20日至11月22日,这一时间段完整的覆盖了“双11”促销策略活动的价格变化。
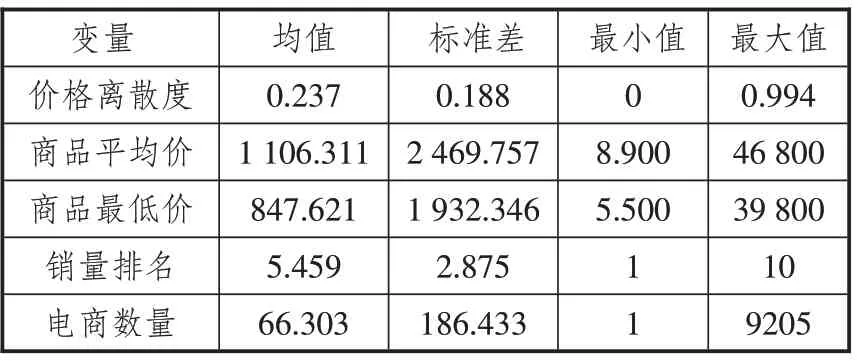
表1 主要变量的描述性统计
四、实证结果与机制分析
(一)电商数量与价格离散度回归结果
基准回归结果见表2,实证结果表明,电商数量越多,价格离散度越高。表2中每一列的含义有所不同。列(1)是未加入控制变量的结果,电商数量增多,价格离散度增大,且两者在1%的显著性水平下正相关。列(2)增加了商品类别和商品品牌的虚拟变量,电商数量的回归系数略有下降,但依旧在1%的显著性水平下正相关,说明部分价格离散度可以由商品类别和品牌解释。列(3)的控制变量更严格,控制商品个体固定效应后,电商数量的影响依旧正向显著,且系数与之前的回归结果非常接近。列(4)同时控制个体固定效应和时间固定效应,回归系数基本不变,双向固定效应模型的回归系数是0.053,说明电商数量每增加1%,价格离散度增加5.3%。
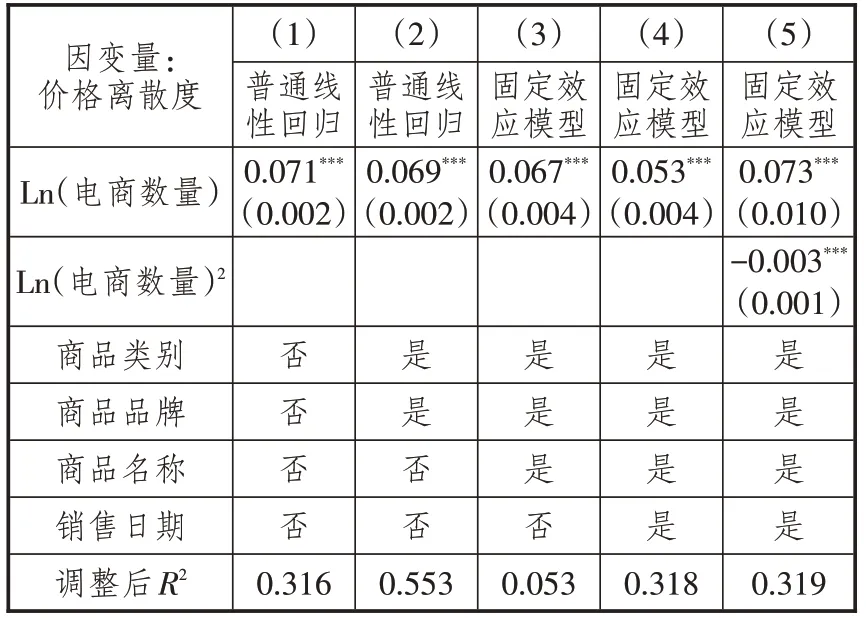
表2 电商数量与价格离散度的回归结果
为考察电商数量与价格离散度的非线性关系,列(5)加入了电商数量平方项作为控制变量,以观察电商数量增多与价格离散度之间的非线性关系。其中,电商数量回归系数的经济含义为电商数量每增加1%,价格离散度增加7.3%。从电商数量平方项的系数值看,随着电商数量的增多,价格离散度增加的幅度边际递减。但从系数值看,递减的幅度非常小。电商数量和价格离散度之间关系的拐点出现在系数值24,由于电商数量取自然对数,因此对应为电商数量的原始数值远超过电商数量在样本中的最大值,说明二次项的拐点已经超出了样本的取值范围。所以,虽然二次项的回归系数为负值,但没有实际的意义。在实际样本中,电商数量和价格离散度之间没有呈现倒U型的关系,仅包含倒U 型曲线的左半段,表现为一条向上倾斜的曲线。
(二)销量排名对价格离散度的影响
通过理论模型的推导,在价格比较网站上排名靠后的商品被消费者搜索到的概率更低,搜索的成本更高,电商数量对价格离散度影响更大。表3展示了10 列不同销量排名下商品的回归结果,采用模型(6)中的回归模型分别做10 次回归,分别对应排名第1到第10的商品的回归方程。由于在前面的回归中,电商数量二次项的拐点已经超出样本的取值范围,加入二次项没有实际意义,所以这里的双向固定效应模型不包含二次项。从表3可以看出,排名第1至第10的不同商品的回归系数不断递增,说明电商数量的增加,对不同排名的商品的价格离散度影响是递增的。
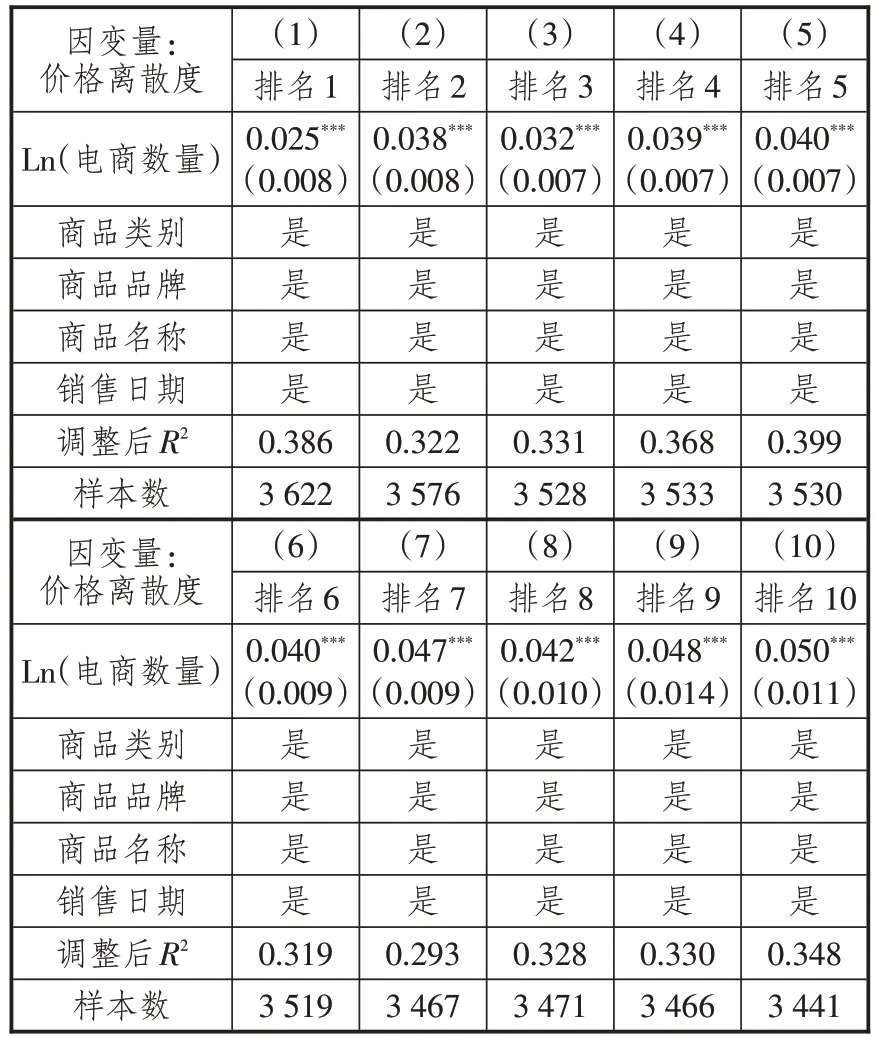
表3 不同销量排名下电商数量对价格离散度的影响
当电商数量增加1%,排名第一的商品价格离散度只增加2.5%,而排名第十的商品价格离散度增加5%,系数大小是排名第一的商品的两倍,说明电商数量对价格离散度的影响越来越大。这一规律在图2中更清晰地表现出来。图2中最上面到最下面的每一行中,回归系数都显著大于零,且呈现出增大的趋势。这验证了假设H2,即排名越后的商品,搜索效率越低,搜索成本越高,价格离散度越大。

图2 不同销量排名下电商数量对价格离散度的影响
(三)稳健性检验
在稳健性检验的部分,结合可能影响导致回归偏误的因素,重新检验电商数量与价格离散度之间的关系,具体的稳健性检验结果参见表4。由于原来定义的离散度是相对值,数据之间的离散程度可能被低估,因此列(1)使用替代的测量指标,用平均值和最低值的绝对差值来测量价格离散度,用全网店铺数的绝对值作为解释变量。在图1中,价格离散概率密度显示被解释变量价格离散度的数据在0的位置有很高的概率密度,说明数据存在零点处被截断的特征,原来的线性回归模型可能存在模型设定误差。表4列(2)采用托宾(Tobit)模型进行估计,该模型可以纠正在零点处有截断的数据分布类型导致的估计偏误。考虑样本选择问题,由于在基准回归中离群值对回归结果的影响,对电商数量的最高1%做截尾处理。列(3)则不对离群值做截尾处理,重新进行回归。从回归结果来看,无论采用哪一种稳健性检验,回归结果都与基准回归结果一致。因此,基准回归结果是稳健的,电商数量的增加会显著提高价格离散度。
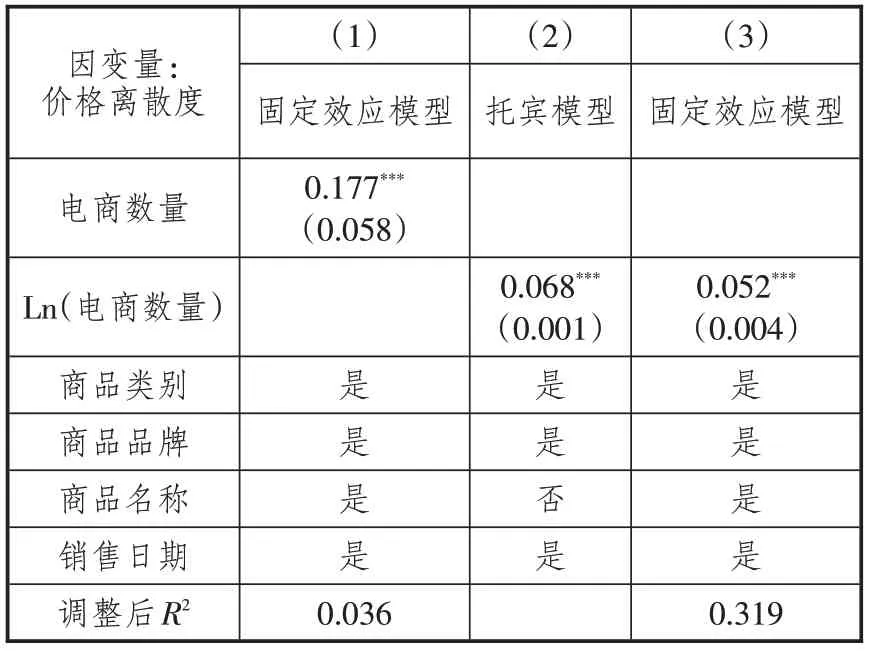
表4 稳健性检验
(四)内生性讨论
基准回归模型采用双向固定效应模型,可以很好地解决以下两种遗漏变量问题:不随时间变化的个体特征以及不随个体变化的时间特征。但依然还有可能有其他的内生性来源需要考虑,下面继续讨论三种可能的内生性来源,内生性讨论的回归结果见表5。
1.遗漏变量偏差
通过选择更加同质化的商品,减小影响价格的遗漏特征因素,商品可能会因为更新换代而提升性能,价格也会相应提升,我们无法控制这部分影响价格的因素。因此,为减少这些遗漏变量对价格的影响,这里选用性能在短期内不会改变或者变化不大的商品。本研究把样本限定在体育用品类,因为体育用品大部分在短时间内不会更新换代。即使有更新换代,其性能和产品特征也不会发生太大的变化。从表5列(1)可以看出,当样本限定在体育用品时,回归结果基本不变。另一种处理遗漏变量偏差的方法是采用倾向得分匹配的方法,表5列(2)所示,将样本的电商数量按中位数分成电商数量多和电商数量少两种商品类型,并且将商品名称、商品性质、品牌、销售日期变量作为控制变量,发现电商数量多的商品价格离散度比电商数量少的商品高出17.2%,并且在1%的水平上显著,与基准回归的结果一致。
2.逆向因果问题
基准回归结果表明,电商数量越多,价格离散度越大,但该结论反过来也有可能成立,即存在较大的价格离散度,意味着该市场依然存在很多竞争的机会,可能吸引更多电商加入,使电商数量增多。为减少这种电商大量进入市场的可能性,本研究把数据的时间范围进一步压缩。由于在“双11”期间大量电商降价促销,所以这里仅保留“双11”前后3 天的数据。在如此短的时间内,电商的进入和退出几乎不可能。所以,逆向因果问题存在的可能性很小,可以集中讨论已有电商数量对价格离散程度的影响。从表5列(3)可以看出,当样本限定在“双11”前后3天的时间内,其回归系数与基准回归结果依然保持一致,只是略有下降,这可能是价格调整时间变短所致。
3.测量误差
本研究数据采用的是价格比较网站数据,需检测电商数量的数据是否存在测量误差。因为有可能价格比较网站所汇聚的电商数量偏少,部分电商没有统计到样本中。为检验这种可能性,根据电商数量中位数将样本分成两类:电商数量较多的样本和电商数量较少的样本。如果电商数量偏少导致测量误差,那么在较少的电商数量样本中更有可能存在测量误差。从表5列(4)可以看到,较少电商数量样本的回归结果与基准回归的结果接近,说明较少电商数量的样本并不存在明显的测量误差。当然,这种推断并不十分严谨,但鉴于获取全网电商数据理论上十分困难,在已有数据的限制条件下,即使存在样本选择产生的偏误,这种偏误也不足以推翻本研究的基本结论。
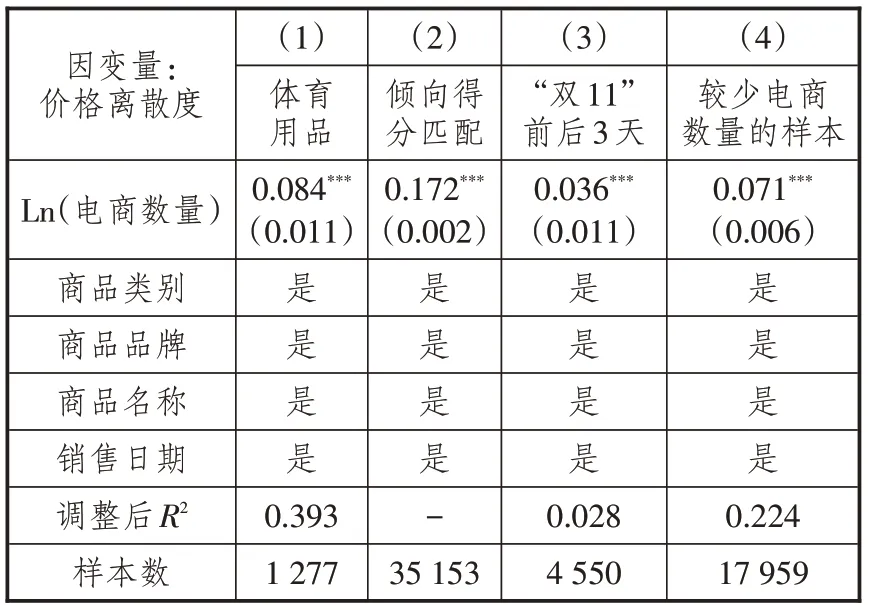
表5 内生性讨论的回归结果
(五)对影响机制的进一步讨论
如果电商间的竞争会使平均价格降低,那么这对消费者是有益的。如果电商间的竞争仅仅通过价格战拉低了最低价,平均价格并没有变化,那么这种价格离散度的变化对消费者福利的影响不确定。在基准回归模型中,将被解释变量分别更换为商品的平均价和最低价,用于检验电商数量对平均价和最低价的影响。表6反映了电商数量对平均价格的回归结果,表7反映了电商数量对最低价格的回归结果。
表6和表7中列(1)至列(5)中控制变量的选取与基准回归表2是一样的。从列(4)的结果可以看出,电商数量对价格平均值的影响不显著,但对最低价有显著的负作用。列(5)是加入电商数量平方项的双向固定效应模型,可以看出拐点的值很大,且不在样本的取值范围内。因此,讨论电商数量二次项的回归系数大小没有实际的意义。这里以列(4)不加入平方项的回归结果作为主要结论。电商数量对平均值的双向固定效应模型的回归系数不显著,但对最低价的回归系数是在1%的水平下显著。电商数量每增加1%,最低价下降0.076%,说明电商数量主要通过价格战的方式拉低最低价来增加价格离散度,而对商品的平均价格没有影响。因此,电商数量增加对消费者福利的作用是利还是弊,本研究没有足够的证据可以做出结论。研究价格对消费者福利的影响,需要进一步收集商品的销售数量,及其在每一个价格节点的概率分布,这是未来研究的一个可扩展的方向。
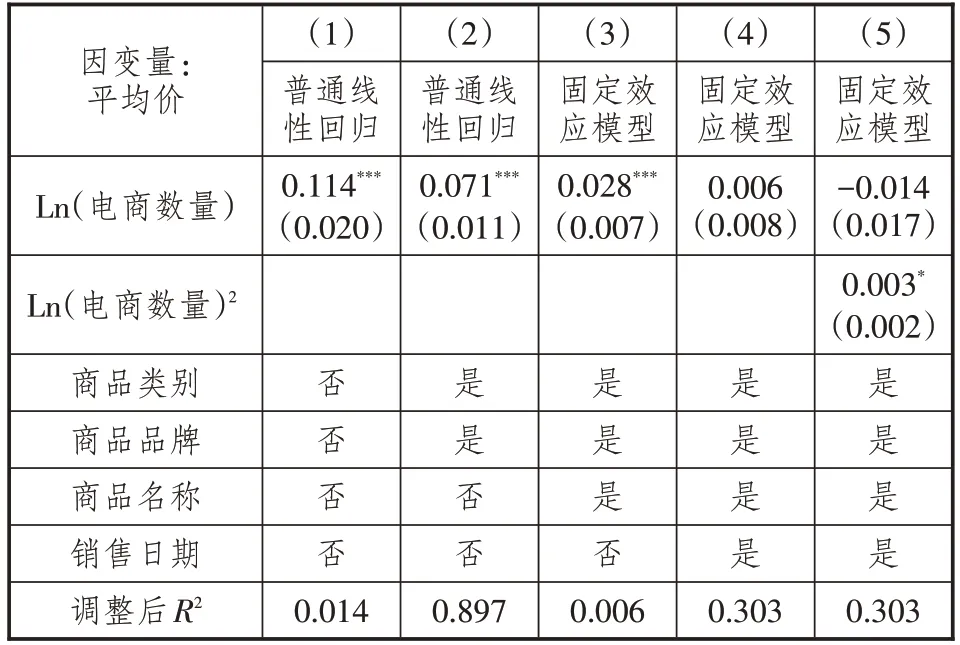
表6 电商数量与平均价格的回归结果
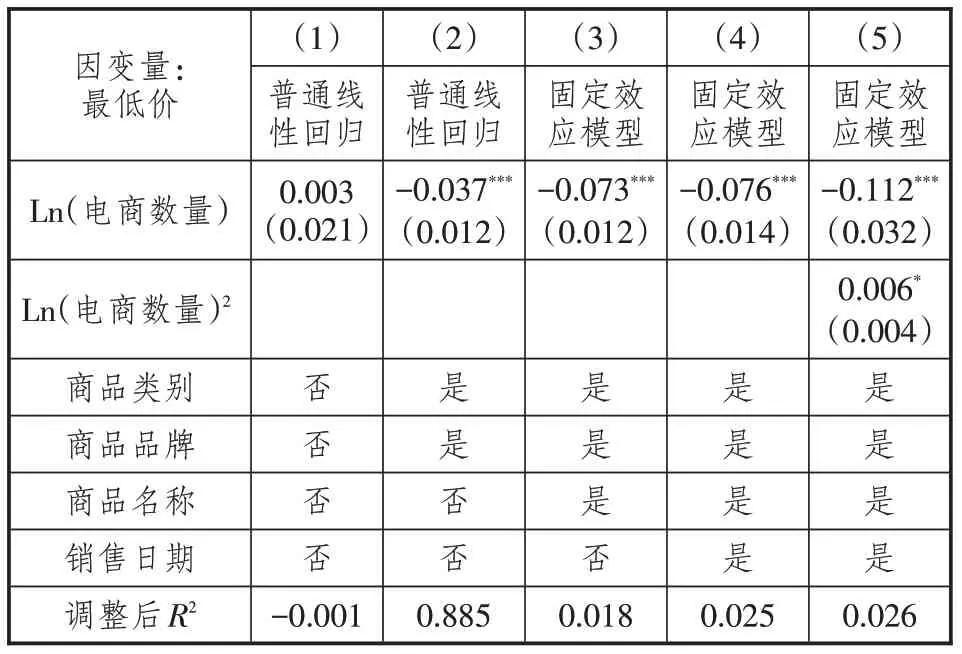
表7 电商数量与最低价格的回归结果
五、结论与建议
近年来,价格比较网站的发展让乐观主义者预言在线商品销售的搜索成本可以降低为零,价格歧视的现象将被终结,价格离散将很难维持。然而,现实中价格离散的现象依然普遍存在。本研究结论表明,价格离散现象并不会随价格比较网站的发展而消失。通过收集中国在线商品价格比较网站的每日销售数据,利用“双11”期间同种商品较大幅度价格变化的数据特征,构建双向固定效应模型,实证检验了电商数量与价格离散度的关系,结果发现:首先,商品的价格离散度随电商数量的增加而增大,在考虑样本选择误差、反向因果和测量误差等内生性来源后,电商数量与商品价格离散度间的正向关系依然稳健;其次,价格比较网站的销量排名有助于降低搜寻成本,排名越靠前,价格离散度越小,更确切地说,排名在前的商品,同样的电商数量增加所带来的价格离散度增加更小;再次,以机制检验分析电商数量对不同价格的影响,发现电商数量主要是通过拉低价格的方式提高价格的离散度,而对商品的平均价格没有影响。
与已有的研究相比,本研究的实证分析具有以下特点:一是本研究使用的是价格比较网站数据,该数据覆盖绝大多数电商的价格,更符合网络销售中消费者跨平台搜寻的实际情况。二是本研究发现价格比较网站的销售排名可以部分降低跨平台搜寻成本,有助于降低价格离散现象,但依然无法消除价格离散。这与雷兵[1]采用仿真实验模拟网络平台排名规则对价格离散影响的研究发现一致。这一发现丰富了微观经济学市场结构的价格决定理论和信息经济学搜寻成本的相关理论。三是本研究对电商数量对价格离散的影响机制进行了讨论,对我国零售电商市场反垄断及其对消费者福利影响的政策制定具有一定参考价值。
本研究结论对制定互联网平台的反垄断政策具有理论指导意义。电商平台的“二选一”现象由来已久,很多互联网平台要求商家只能在本平台销售,并通过算法和排名控制商家的被搜索量。电商平台通过复杂的算法和排名的方式使排名靠前的商品更容易被消费者搜索到,并提高了排名靠后的商品隐含的搜寻成本。这在某种程度上提高了平台对消费者实施价格歧视的能力,导致电商销售出现强者愈强、弱者愈弱的两极分化现象。通过对价格排名网站的研究,发现价格排名网站作为提高搜索效率的工具,可以部分降低电商对消费者的价格歧视,实现线上商品在多平台销售,有利于增加平台间的竞争,约束电商平台的垄断定价权,保护消费者的利益。因此,政府可以对电商平台实施相应的约束和管制,不允许电商平台强制用户“二选一”,对消费者跨平台选择的权利提供法律保障。
本研究结论对打破行业垄断和促进互联网行业的健康发展具有启发意义。《2019年度中国网络零售市场数据监测报告》显示,以网站成交总额计算,天猫和京东分别占据50.1%和26.5%的市场份额,寡头垄断的趋势日益严重。因此,在平台经济背景下,政府应通过鼓励并促进类似于价格排名网站的网络平台的发展,降低消费者的搜寻成本和厂商的信息交换成本,打破少数企业对网络销售的垄断地位,促使互联网行业建立更开放、多元的生态体系,让消费者有更多的选择权和议价权,从而改善消费者的福利。
注释:
①数据来源于商务部网站https://www.samr.gov.cn/wljys/ptjj⁃yj/202110/t20211008_335398.html。
