考虑风电和负荷不确定性的输电网多目标柔性规划

王娟娟，王涛，刘子菡，朱海南，李丰硕，孙华忠

(1.国网山东省电力公司潍坊供电公司，山东 潍坊 261014；2.山东大学 电气工程学院，山东 济南 250061)

0 引言

由于风力发电具有波动性与随机性的特点[1-4]，风电渗透率的提高增加了电网的不确定性因素[5-7]，给电力系统带来前所未有的挑战[8-10]。

风电渗透率不断提高使输电网规划不仅需要考虑经济性[11]、运行效率[12]等要求，还要承受住风电和负荷不确定性波动的考验[13-17]。因此，考虑不确定性的输电网多目标柔性规划得到了广泛研究，目前广泛使用的方法包含机会约束、概率潮流、多场景技术等。文献[18]考虑到风电并网带来的不确定性，构建了考虑全寿命周期内系统经济成本最小和切负荷量最小的规划模型。文献[19]基于直流概率潮流模型，利用机会约束规划方法构建了考虑线路总长度和风电场发生电压闪变情况的规划模型。文献[20]利用多场景概率抽样算法，构建了考虑全寿命周期内的经济成本、输电带来的总体收益和输电线路过负荷的规划模型。文献[21]基于多场景构建技术，建立了基于N−1系统安全性校验的规划模型。

基于直流潮流构建输电网规划模型[22]具有简单、求解效率高的优点，但其忽略了电压幅值变化和无功潮流，尤其是在输电网中无功潮流会占据相当一部分线路容量。因此，对于高电压等级输电网的规划问题采用直流潮流无法反映系统真实情况。基于交流潮流方程的规划类研究逐渐受到重视[23-25]，将交流潮流模型转化为二阶锥规划模型进行求解的凸松弛等数学方法[26-29]，在保持求解精度的前提下能够显著提升求解效率，但在输电网规划中尚未得到应用。

本文建立了考虑风电和负荷不确定性的输电网多目标柔性规划双层模型，以调整后的39节点测系统为例，分析所提方法的有效性和可行性。

1 考虑风电和负荷不确定性的场景

本文研究的输电网风电和负荷不确定性主要体现在风电场出力受风速影响以及负荷需求的随机波动。利用历史风速和负荷数据通过参数估计构建风电出力和负荷的概率分布模型，进而对风电和负荷的概率分布模型进行蒙特卡洛抽样，生成反映风电和负荷不确定性的随机场景。随机场景数量过多会使模型求解困难，因此采用k-means聚类算法对随机场景进行聚类。

1.1 风电和负荷的概率分布模型

1.1.1 风电出力概率分布模型

风电场出力由风速决定，通常采用两参数威布尔分布模型拟合风速概率分布情况。其分布函数和概率密度函数[30-31]分别为

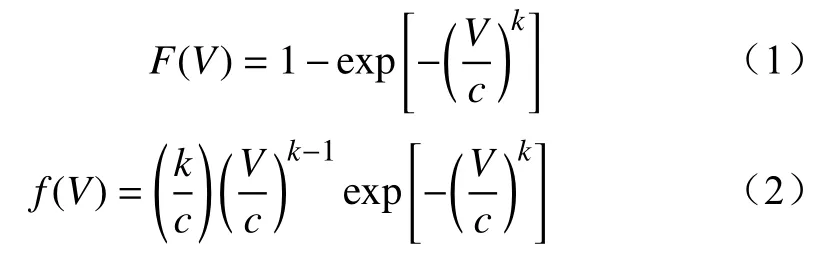
式中：k为反映风速变化的形状参数；c为反映平均风速的尺度参数；V为给定的风电场风速数值。

通过矩估计法可以获得历史风速数据服从概率分布的分布参数，从而得到能够反映实际风速状况的威布尔分布模型。

风电场的有功功率PW与风速v对应的函数关系为

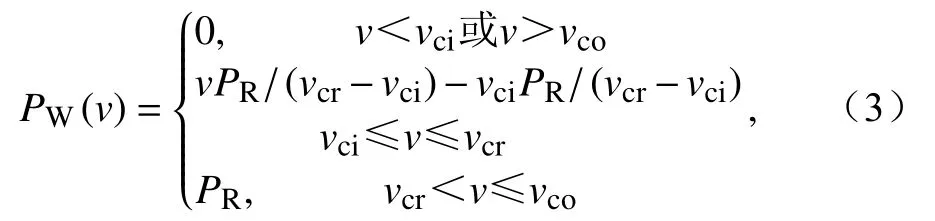
式中：v为风电场实际风速；vci、vcr、vco分别为切入风速、额定风速与切出风速；PR为风电场的额定有功功率。

1.1.2 考虑空间相关性的风电场模型

风电场出力和风速大小密切相关，而相邻风电场出力由于气候与环境相似而具有很强的相关性，因此需要考虑风电场间彼此的空间相关性，基于正态Copula函数建立风电场的联合概率分布模型。

根据多元分布Sklar定理，Copula函数可将随机变量x1,x2,···,xn的边缘分布函数F1(x1),F2(x2),···,Fn(xn)联合为联合分布函数H(x1,x2,···,xn)，即

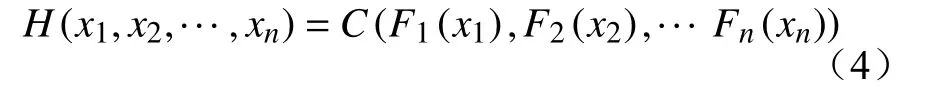
对式（4）两边同时求偏导，得到随机向量X=(x1,x2,···,xn)的联合概率密度函数h(X)为

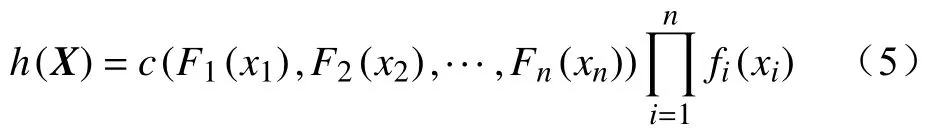
式中：c（∙）为Copula概率密度函数；fi(xi)为xi的概率密度函数。

1.1.3 负荷的概率分布模型

城市用电负荷大小和居民日常生产生活息息相关，并且呈现很规律的日特性，负荷的概率分布特性近似服从正态分布，可表示为

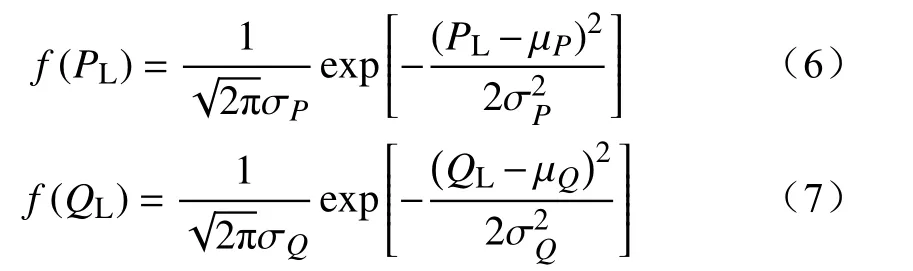
式中：µ与 σ分别为负荷概率分布的均值和标准差，其值可根据历史负荷数据进行参数估计得到。

1.2 典型场景构建方法

风电不确定性模拟的方法为：首先根据历史风电场出力求得风电出力的概率密度和概率分布函数，然后构建N维Copula函数并求解Copula函数相关系数，最后进行蒙特卡洛抽样生成大量具有相关性的随机值，对随机值求逆即可得到风电的模拟场景数据；负荷场景模拟方法类似，只是不需要进行联合概率分布建模。

利用蒙特卡洛抽样进行系统状态抽样生成了大量随机场景，使规划模型求解难度和计算量过大，因此，利用基于伪F-统计的k-means聚类算法对获取的数据进行聚类分析，得到反映风电和负荷不确定性的典型场景，这样既能充分反映风电和负荷的不确定性又可显著提升求解效率。

2 多目标规划上层模型

上层规划模型基于交流潮流，采用综合考虑建设投资等年值费用、年网损费用和运行效率的多目标规划模型，对风电场接入后输电网的新建线路方案进行决策。与传统的基于直流潮流的输电网规划模型相比，本文的上层模型能够获得电网的无功潮流和更加准确的有功潮流，使规划结果更加准确可靠。采用多目标规划可以获得兼顾多个目标，无决策者偏好地进行规划，从而帮助决策者进行权衡。

2.1 上层模型目标函数

建设投资等年值费用目标为

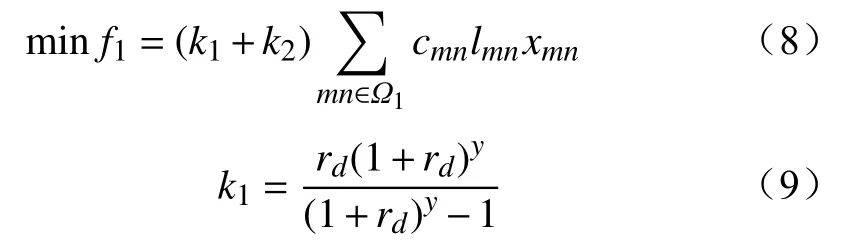
式中：f1为规划方案的建设投资等年值费用；k1为资金回收系数；k2为工程固定运行费用率；cmn为节点m与n间待建线路单位长度造价；xmn为节点m与n间新建线路回路数；lmn为节点m与n间待建线路的长度；Ω1为待选新建线路集合；rd为贴现率；y为工程经济使用年限。

年网损费用目标为

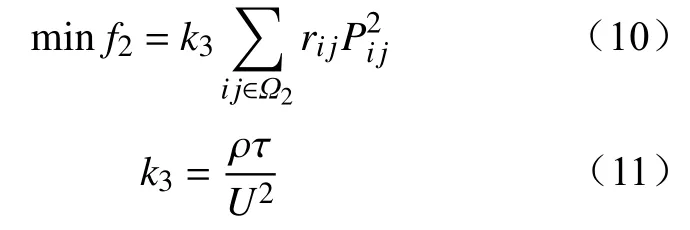
式中：f2为可变运行费用，反映规划方案在运行期间的经济性；k3为年网损费用系数；rij为线路ij的电阻；Pij为正常情况下线路ij输送的有功功率；Ω2为网络中已有和新建的线路集合；ρ为网损的单位电价；τ为最大负荷损耗时间；U为系统额定电压。

采用线路平均负载率反映线路年实际输送电量占理论最大经济输送电量的比例。为了将问题统一为最小化多目标优化，取该地区该电压等级输电线路平均负载率的倒数为子目标，可表示为

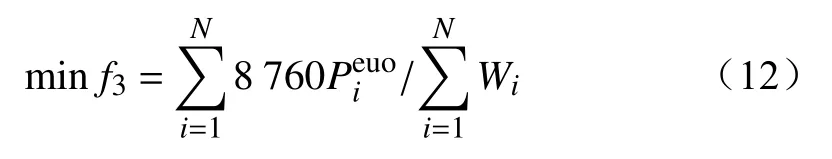
式中：Wi为第i条线路累计输送电量；为第i条线路经济输送容量。

2.2 上层模型约束条件

上层规划模型以上述3个指标为目标，需满足的约束为

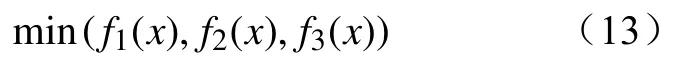
（1）决策变量的取值范围，每条输电走廊的新建线路回路上限约束为

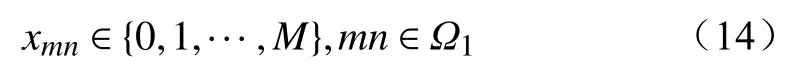
式中：xmn为输电走廊mn的待建回路数，其上限M本文取3。

（2）系统同期并列和稳定运行对节点电压的幅值和相角约束为

（3）输电线路正常运行需要满足交流潮流平衡约束为

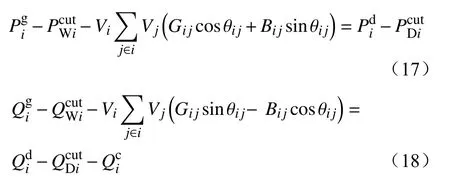
（4）线路潮流上限约束为

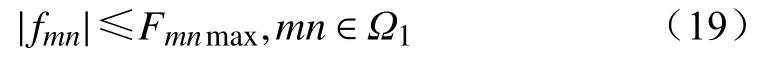
式中：节点m、n之间线路的实际潮流fmn不应该超过线路容量Fmnmax。

（5）常规发电机组出力上下限约束为

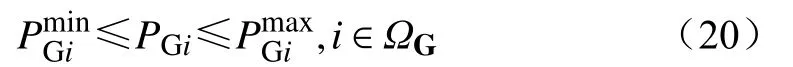
式中：PGi为节点i处常规发电机组的有功出力；分别为常规发电机组的出力上、下限。

（6）弃风容量约束为

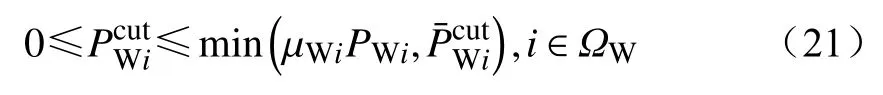
式中：µWi为节点i容许弃风的最大比例系数；PWi为节点i处风电机组的有功出力；为下层返回给上层的弃风容量期望值。

（7）切负荷量约束为

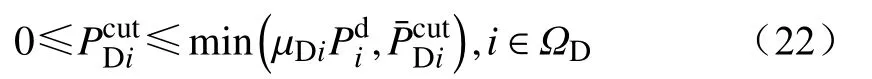
式中：µDi为节点i容许切负荷的最大比例系数；为节点i处有功负荷量；为下层返回给上层的切负荷容量期望值。

3 多场景校验下层模型

下层规划模型利用蒙特卡洛抽样和基于伪F-统计的k-means聚类算法获得的典型场景，校验上层规划的帕累托最优规划方案集合对风电出力与负荷随机波动等不确定性因素的承受能力。

3.1 下层模型目标函数与约束条件

构建以各典型场景下弃风惩罚与切负荷惩罚量之和最小为目标的优化模型，可表示为

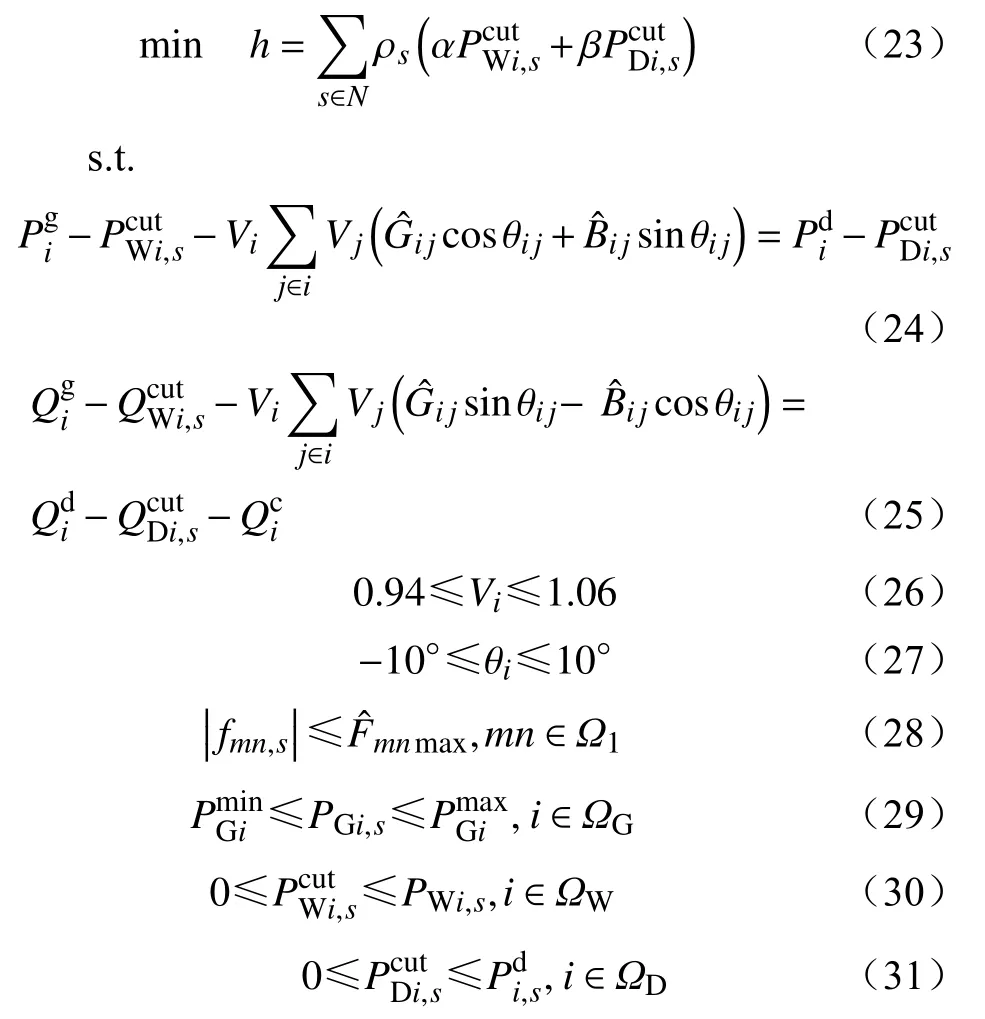
式中：ρs表示典型场景s发生的概率；N为典型场景数；式（24）～（31）都是在上层帕累托最优解集中线路扩建方案基础上，针对每个典型场景s下的约束条件和变量，约束条件与上层基本一致，在此不再赘述。

3.2 交流潮流方程的二阶锥近似

式（24）和（25）是一组非线性方程，传统的非线性规划方法均为单路径寻优模式，存在全局寻优能力不足等问题。因此，普遍采用智能算法求解。但本文提出的下层规划模型需要对帕累托最优解集中所有规划方案在多个典型场景中进行计算，相比于上层规划模型只对确定性场景进行规划，下层模型计算量显著增加，采用智能算法的求解效率不理想。因此，需要能够兼顾计算精度和效率的方法求解该问题。本文将非线性且非凸的交流潮流表达式（24）（25）凸化为具有凸锥特性的二阶锥约束，从而建立了基于交流潮流方程的二阶锥近似模型。

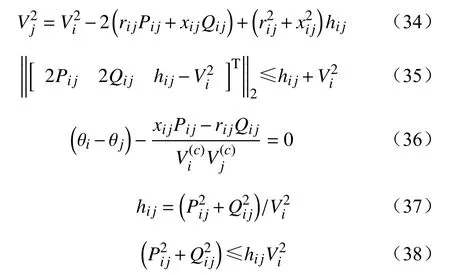
二阶锥近似后的规划模型从本质上变化为一种凸规划，解的最优性和计算高效性都能够满足计算精度的要求。利用Cplex求解器可以进行快速求解。

4 求解方法与流程

4.1 上下层模型求解方法

上层模型为混合整数非线性多目标规划模型，采用带有精英保留策略的快速非支配排序遗传算法（non-dominated sorting genetic algorithm-II，NSGA-II）求解。下层规划为二阶锥规划模型，本文用Cplex求解器进行求解，可以显著提高运算效率。

4.2 上下层模型迭代方法

在双层输电网多目标规划模型中，将上层规划方案获得的帕累托最优规划方案集合传递给下层。下层问题利用蒙特卡洛抽样和聚类算法获得的典型场景对帕累托最优规划方案集合中所有的规划方案进行校验，求取不同典型场景下的弃风量和切负荷量，并根据不同典型场景的概率函数加权计算规划方案的弃风量期望值和切负荷量期望值，如果期望值低于最大弃风率和最大切负荷率限制，说明该方案通过了下层不确定性校验，否则不通过校验。取所有通过校验方案中各风电场节点和负荷节点的弃风和切负荷量的最大值，作为下层整体的弃风切负荷期望值反馈给上层模型，并修改上层模型中式（21）和（22）的弃风和切负荷的相关参数。由于返回的期望值能够反映通过不确定性校验的方案在各节点上的弃风和切负荷的上限，能够有效辅助上层规划模型获得计及多场景下不确定性因素的最优输电线路规划方案。系统的迭代终止条件是连续两次传递期望值的相对差值小于给定值。该迭代终止条件要求该方案在不确定性因素校验下，弃风量期望值和切负荷量期望值趋于稳定，从而满足系统收敛性的要求；如果不满足迭代终止条件，需要在弃风和切负荷期望的指导下重新进行上层规划。上下层模型反复迭代直到满足精度要求。

5 算例分析

5.1 算例介绍

为说明所提出的双层规划模型的有效性，本文利用调整后的IEEE39节点系统进行算例分析。假设在规划水平年2020年该系统新建2个风电场，分别位于40和41节点，额定装机容量分别为390 MW和490 MW，约占总负荷容量的12.3%，新建线路数上限为3条。用来拟合概率分布函数的负荷历史数据与风速历史数据采用山东省2015—2019年标么化的数据。图1和图2展示了对应的8个风电典型场景和8个负荷典型场景。

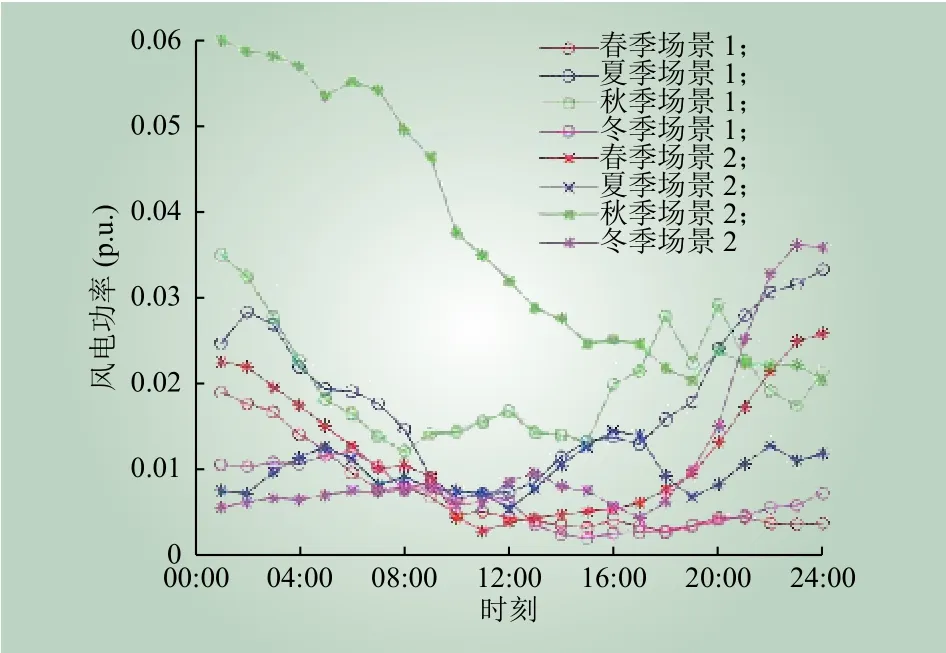
图1 风电典型场景Fig.1 Typical scenarios of wind power

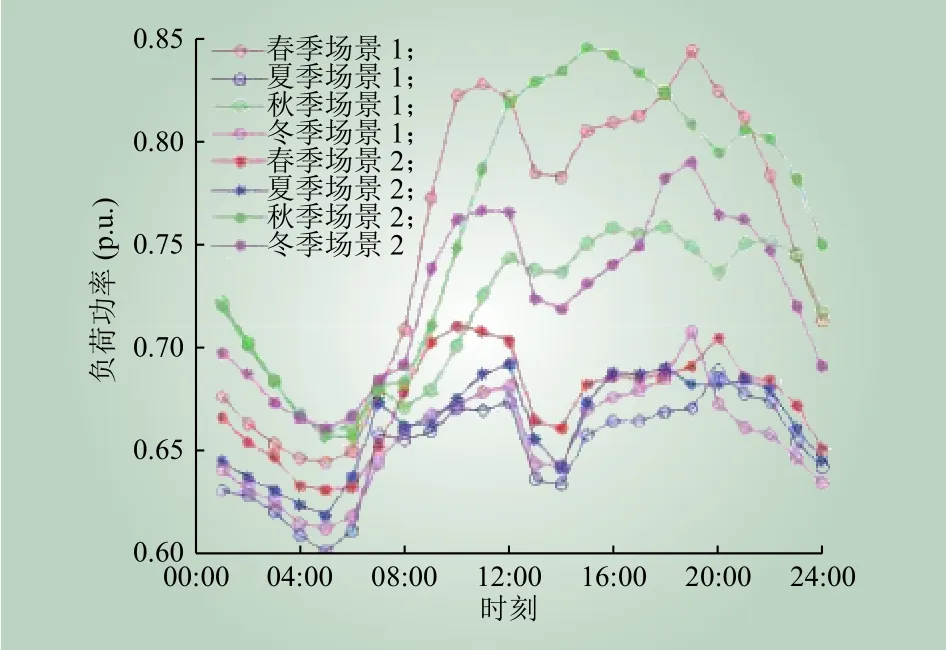
图2 负荷典型场景Fig.2 Typical scenarios of load

5.2 仿真结果分析

经过计算，得到了非支配等级为1的帕累托最优解集，根据建设投资等年值费用从小到大排序，得到新建线路的决策结果如表1所示。

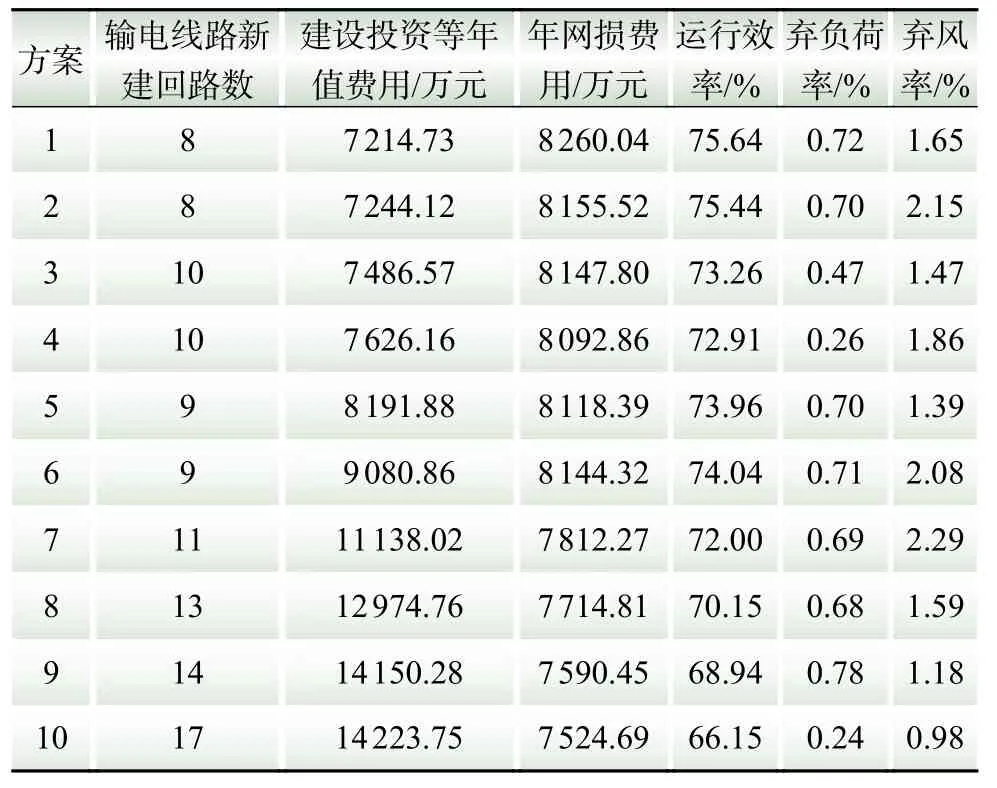
表1 部分帕累托前沿解Table 1 Part solution for the Pareto fronts

表1中的方案具体新建线路结果如表2所示，其新建线路回路数由括号里数字表示。

表2 输电系统规划方案Table 2 Transmission network planning schemes

与单目标优化问题不同，在多目标优化问题中的多个目标函数值很有可能存在矛盾，不可能同时达到最优。由表1可以看出，在帕累托前沿解中，各方案呈现出新建回路数越多，建设投资等年值费用越大的特点。但在方案5和方案6新建线路数低于方案3和方案4，这是由于方案5和方案6中的部分线路长度较长。但随着新建回路数越多，系统年网损费用越低，运行效率也越低。因此，建设投资等年值费用目标和年网损费用目标矛盾，也与运行效率目标矛盾。

由此可见本文提出的多目标柔性规划模型不仅能求取到某个指标最优的解，还能同时分析其他指标的优劣情况以及各个指标之间的相互关系。对帕累托最优解按照运行效率排序后，发现最优方案仍是表1中的方案1，并且其建设投资费用与年网损费用之和最低，弃风率低于2.00%，弃负荷率低于1.00%，因此选取方案1为最优方案。新建线路具体情况如图3所示，其中黑色实线代表原本输电系统，红色虚线代表规划所得的待建线路。

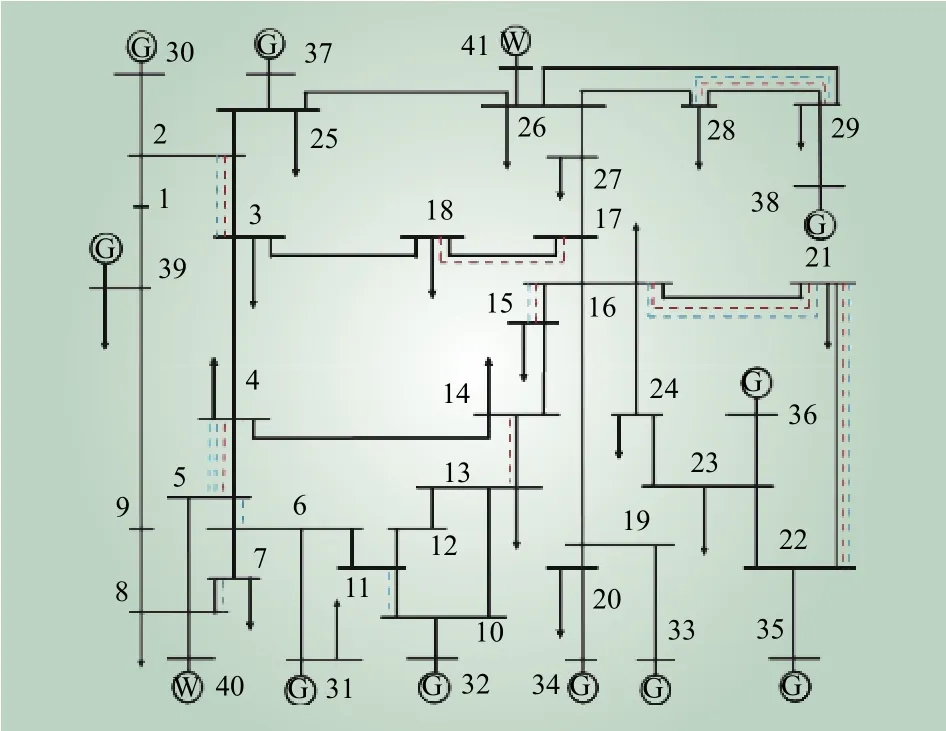
图3 输电系统规划结果Fig.3 Transmission network planning results

由图3可见，方案1规划的输电线路一部分分布在新增风电场的周边区域，能够帮助系统接纳风电出力，另一部分分布在负荷增多的节点17、21附近，新建线路很好地满足系统的供需变化，证明了模型的有效性。

5.3 算例对比分析

5.3.1 柔性对比分析

为验证本文提出的输电网柔性规划模型能承受源荷不确定性的波动，现对确定性场景下的输电网多目标规划模型进行算例求解，即仅由上层模型求得规划方案。经过NSGA-II算法求解得到了帕累托最优解，表3展示了其建设投资等年值费用最优的前10个方案。

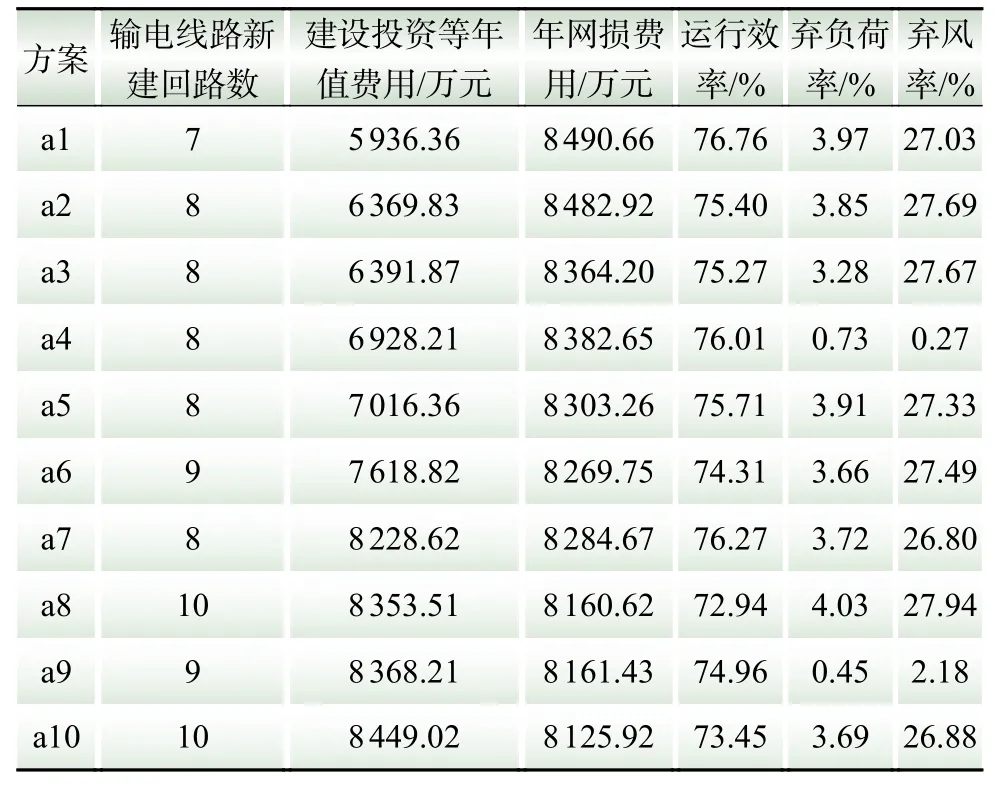
表3 确定性模型的部分帕累托前沿解Table 3 Part solution for Pareto fronts of deterministic model

对比表1和表3列出的帕累托前沿解集，确定性模型解集的新建线路数减少22%，建设投资等年值费用减少26%，年网损费用减少4%，运行效率提高4%，但是弃负荷率增大为4倍，弃风率增大为13倍，说明此确定性模型并不能承受风电和负荷不确定波动的考验，也说明本文建立的双层柔性规划模型充分考虑了风电和负荷的不确定性变化。相比之下，本文提出的双层规划模型经过下层模型多场景校验的修正以及与上层模型的不断迭代，求解结果能够兼顾经济性和运行效率，又能保证在源荷不确定性影响下系统的弃风率和弃负荷率较小。由此可见，本文提出的输电网多目标柔性规划模型在接受牺牲部分经济性代价的前提下，可以较好地适应随机变量概率分布的不确定性。

5.3.2 风电渗透率影响分析

调整新增风电场规模，在节点40增加180 MW容量，提高风电渗透率。重新利用本文建立的双层多目标柔性规划模型进行计算，同样按照建设投资等年值费用排序，部分计算结果如表4所示。

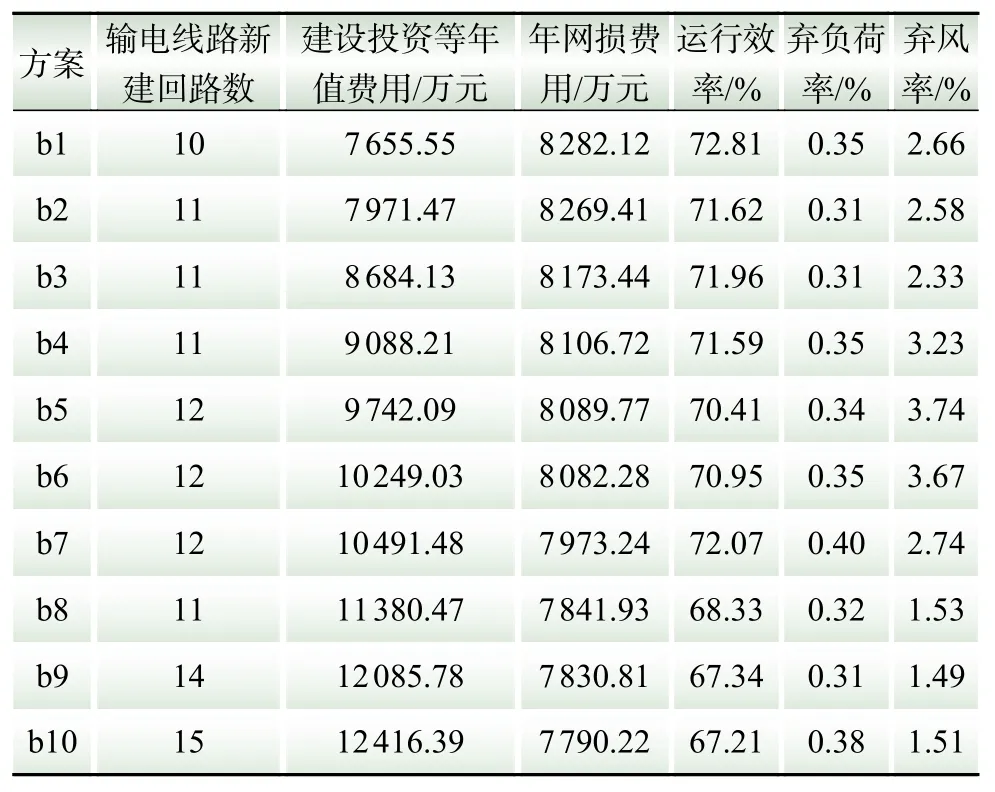
表4 更高风电渗透率系统的部分帕累托前沿解Table 4 Part solution for Pareto fronts of the power system with high penetration of wind power

对表4中的结果进行分析，发现方案b1的建设投资等年值费用与年网损费用之和最低，且运行效率最高，因此选取方案b1为最优方案。方案b1的具体新建线路结果如表5和图3中蓝色虚线所示。对比分析表4与表1，发现风电的渗透率提高20%时，帕累托前沿解集的新建线路回路数增加9%，建设投资等年值费用增加0.4%，年网损费用增加1.1%，运行效率降低2.52%，弃负荷率降低42%，弃风率提高53%。可见风电渗透率提高，有利于电网供应更多的负荷，但同时弃风率也会增大，经济性成本也小幅增加。

表5 含更高风电渗透率系统的规划方案Table 5 Planning schemes of the power system with high penetration of wind power

对比图3中的红色虚线和蓝色虚线规划结果可以看出，新建线路的决策结果发生变化，新建线路回路数增多，风电渗透率主要影响局部规划方案，更高风电渗透率系统的新建线路略多，主要集中在风电机组增加的区域附近，求解方案直观展示了模型对于系统风电渗透率提高的处理，也说明本研究提出的双层多目标柔性规划模型对于风电渗透率的提高有很强的适应性，符合中国风电快速发展的形势，有较强的实际应用价值。

6 结语

当前考虑风电和负荷不确定性的输电网规划模型大多采用直流潮流，忽略了电压幅值变化和无功潮流分布，从而影响规划结果的准确性，本文基于交流潮流方程，构建了考虑风电和负荷不确定性的输电网多目标柔性规划双层模型。

上层输电网多目标规划模型考虑了建设投资等年值费用、年网损费用和运行效率目标，采用带精英策略的非支配排序遗传算法求解并将帕累托最优规划方案集合传递给下层；下层模型充分考虑了电源出力的不确定性和风电场间出力的相关性，利用风电和负荷历史数据，通过蒙特卡洛抽样和聚类生成描述风电和负荷不确定性的典型场景，并计算典型场景下的弃风和切负荷量最小值，以校验最优规划方案集合对于风电和负荷不确定性的承受能力。用下层模型的弃风和切负荷期望值修改上层模型的约束条件，上下层模型相互约束共同进化。

为了降低求解难度，对非线性且非凸的交流潮流方程进行二阶锥松弛，使复杂的非线性规划模型转化为具有凸可行域的二阶锥规划模型，求解效率显著提升。算例分析表明，与确定性模型相比，双层模型得到的规划方案牺牲一定的经济性，显著降低了多场景校验时系统的弃风和切负荷量，对风电和负荷不确定性波动具有更强的适应能力；风电渗透率影响分析后发现，本研究提出的双层多目标柔性规划模型对于风电渗透率的提高有很强的适应性，为风电大量并网背景下的输电网规划提供了新的思路。