满秩分解最小二乘法船舶航向模型辨识
2022-02-18包政凯朱齐丹刘永超
包政凯,朱齐丹,刘永超
(哈尔滨工程大学 智能科学与工程学院, 黑龙江 哈尔滨 150001)
随着数字化和智能化技术的发展,智能船舶发展呈现出日益加快的趋势[1-3]。我国目前处于《智能船舶发展行动计划2019-2021年》提到的三年目标阶段,正在实现智能船1.0向智能船2.0的过渡。自动靠离泊、远程遥控、自主航行等智能船典型应用场景需要精确的船舶航向自适应控制算法[4-7]。国内已产品化的航向控制器与国外先进产品相比,航向精度、能耗、转向快速性和转向平稳性等性能指标仍有较大差距,主要原因有:1) 航向模型参数在线辨识的实时性、收敛性和辨识精度难以同时保证,在线估计时变参数和扰动的能力不够;2) 海洋高频扰动、测量噪声和测量病态引起的航向角速度信号波动处理困难;3) 舵角控制环应对航速和海况变化的自适应能力不足;4) 操舵执行机构性能受限,与国外接近实现连续控制效果有较大差距。
针对上述第一个问题,目前常用的船舶航向模型参数辨识算法主要分为2类:自校正自适应和模型参考自适应[8]。自校正自适应常用的辨识算法包括最小二乘法[9-14]、支持向量机[15-21]、神经网络[22-24]、极大似然估计[25]、遗传算法[26]等。文献[11]采用最小二乘算法辨识船舶操纵模型的参数,并引入新型的学习率,提升了辨识精度。文献[12]针对船舶响应模型参数辨识问题,在最小二乘算法递推迭代过程中将单新息拓展为多新息,大大改进了辨识算法的准确性。文献[13]为了提升辨识过程的快速性,通过构造辨识误差的评价函数,提出了一种动态遗忘因子最小二乘辨识算法。文献[14]在船舶模型辨识最小二乘算法中引入一个非线性的反正切函数来处理新息,有效地提升了算法的辨识精度。文献[18-20]采用支持向量机对船舶航向模型参数进行辨识研究。支持向量机具有全局最优搜索能力,得到的模型泛化能力强,结合优化算法可以提升辨识精度并简化调参。文献[21]调查了船舶操纵运动的水动力模型,将神经网络应用到船舶操纵模型和三自由度模型辨识中。文献[22]针对大型油船的参数辨识问题,提出了基于人工神经网络的参数辨识方法。文献[23]提出了油轮转向数学模型,通过广义椭球基函数神经网络算法辨识转向模型参数。神经网络辨识模型参数对初值没有依赖性,并且可以保证辨识参数的收敛性。文献[25]针对水面无人艇操纵性预报问题,利用极大似然法辨识无人艇参数,采用辨识的结果预报了无人艇的操纵运动。文献[26]利用船舶操纵模型的航向角数据构造目标函数,然后选择遗传算法进行寻优,提升了辨识效率。模型参考自适应[27]设计方法中,采用构造李雅普诺夫函数,并与航向控制器联合设计,可以保证模型参数辨识李雅普诺夫意义下稳定,同时实现航向渐进稳定。
上述方法对于提高模型参数辨识精度、收敛速度和实时性有很多贡献,但缺乏对辨识算法收敛性分析。工程中通常使用满足数据激励条件的回转、Z型、自由航行实验数据来保证模型辨识算法的收敛性,但在自适应控制过程中,持续激励条件往往无法满足,使得参数辨识瞬时收敛性问题成为自校正自适应控制的难点。对于数据长时间欠激励、受扰条件下如何保证或提升在线辨识算法的收敛性问题还没有被解决。
本文针对数据欠激励受扰系统,设计了一种快速、准确、稳定的线性模型在线辨识通用方法,并将该算法应用于船舶航向模型参数在线辨识过程中。将动态降维的思想引入遗忘因子最小二乘法 (forgetting factor least square algorithm, FFLS),提出了一种基于满秩分解的最小二乘法(full rank decomposition least square algorithm, FRDLS),使得欠激励数据对降维后的辨识模型重新满足激励条件。所提供的算法能够根据死区阈值动态调整满秩分解矩阵,使最小二乘法选择性更新模型参数,限制了扰动导致的参数辨识误差累计。在样本数据长时间欠激励, 海洋环境干扰工况下,将实船数据用于航向模型参数辨识,对比FFLS和FRDLS算法、多新息最小二乘法[12](multi-innovation least square algorithm, MILS)、最小二乘支持向量机[19](least square support vector machines algorithm, LSSVM)辨识船舶操纵模型参数的辨识结果曲线和航向角速度预报误差曲线,可以发现满秩分解最小二乘法能有效抑制数据欠激励和存在海洋环境扰动时参数辨识过程中的漂移和发散问题,并提高参数辨识的精度,同时具有计算量小、实时性强、简单易实现的优点。
1 船舶航向模型和基本辨识算法
远洋航行的船舶多工作在航向保持模式下,该工况下,船舶自动舵通过给定小舵角抵抗海洋环境干扰,使实际航向保持在期望航向误差带内,辨识准确的航向模型参数是实现高精度航向控制的前提。
1.1 船舶航向模型
船舶操纵运动模型可以采用一阶线性Nomoto 模型[13]:

式中:r为船体艏摇角速度;r˙为艏摇角加速度;φ为船舶艏向角;δ为舵角;K、T为船舶回转能力和回转惯性参数,受到船舶载荷条件和航行速度的影响。最小二乘改进模型辨识算法非常依赖于经典状态空间模型参数,实际工程中考虑到外界扰动和模型摄动对参数辨识的不利影响,此处引入扰动项对Nomoto模型进行改进:

式(2)中 δd为干扰力矩等效舵角,包含了舵的零位误差、船舶航向模型非线性、测量噪声中的非零均值部分、海洋环境扰动力矩等。为辨识做准备,将改进Nomoto模型整理为标准最小二乘形式。

为了加快参数辨识收敛速度,引入归一化因子 αr˙和 αr,辨识前通常使 用归一化因子使数据 向量各维度具有相同幅值范围,令:

选取输出量zk、参数向量 θk、数据向量hk,下标k代表第k时刻:
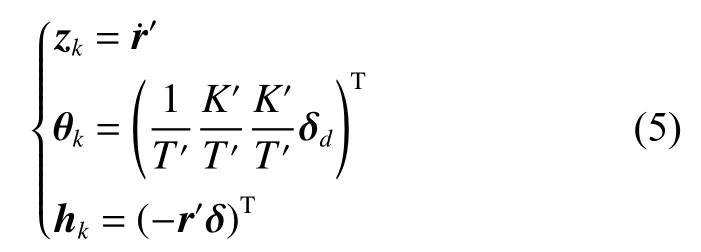
整理得最小二乘测量方程为

式中wk为k时刻测量噪声。
1.2 遗忘因子最小二乘法
递推最小二乘算法因其简单、实时性强的优点,广泛应用于模型参数在线辨识。设给定数据集,其中,hk=[hk1hk2···hkn]T为一次测量数据 向 量 , 令 数 据 矩 阵 为H=[h1h2···hN]T∈ RN×n,输出矩阵为Z=[z1z2···zN]T,则线性回归方程可以表示为

式中: θ =[θ1θ2···θn]T为待估计系数向量;w=[w1w2···wN]T为N次测量的模型拟合误差向量;θ=[θ1θ2···θn]T为待辨识参数数量。最小二乘法(least square algorithm, LS)采用误差向量二范数为损失函数:


矩阵H的秩 R ank(H)=n时,HTH可逆,由式(9)可得 θ的最小二乘估计:
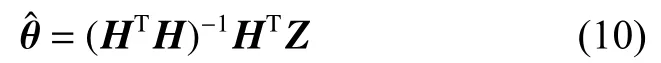
为了将最小二乘转化为递推形式,可令k时刻数据矩阵、测量矩阵、方差矩阵和辨识结果矩阵分别为
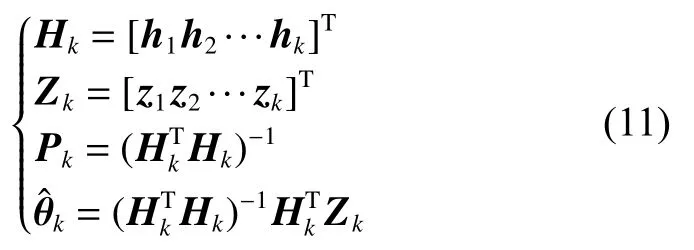
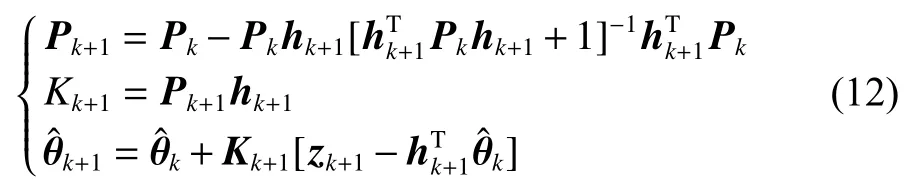
为避免随着数据增多,新数据作用逐渐消失,引入遗忘因子 β1(0.9< β1<1) 得:
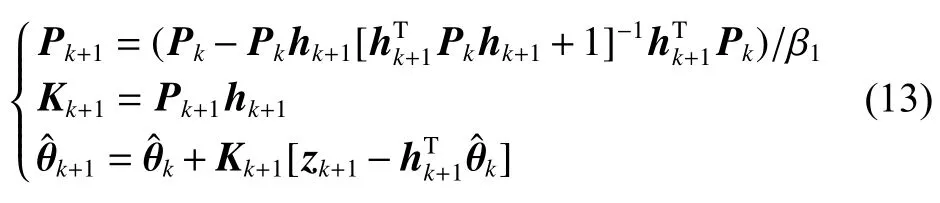
2 基于满秩分解的最小二乘算法设计
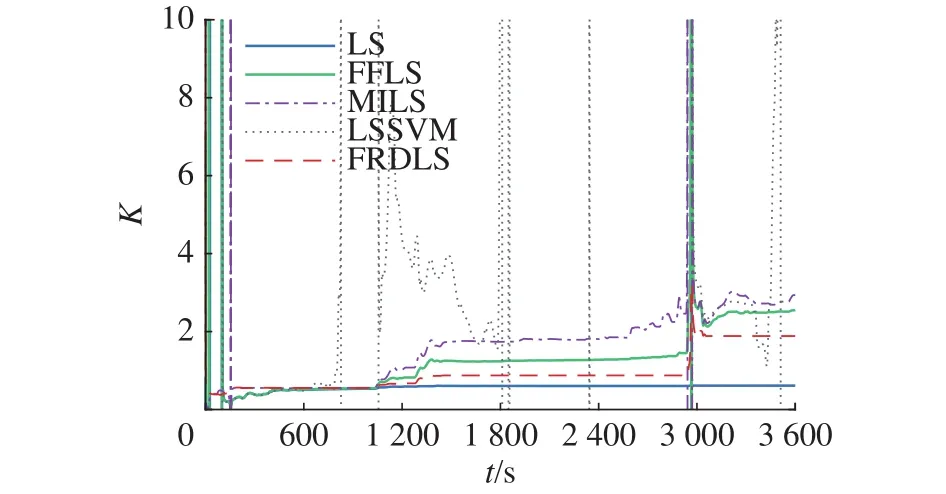
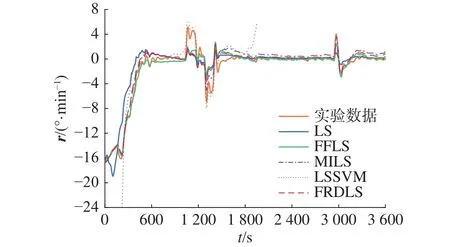
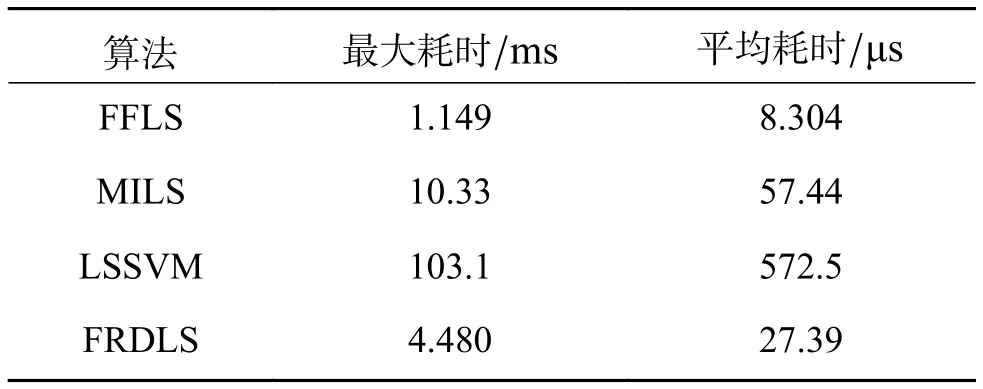
当式(8)中矩阵H的秩r=Rank(H) 式中: 正交投影变换矩阵V的选取不唯一,本文结合递推最小二乘法给出V的一种求解方法。设第k次测量数据 {hk,zk}对应的变换阵为Vk=[Vk1Vk2]。 式中:ei为第i行为1,其余行为0的n维列向量;hs为死区阈值,用于削弱干扰的影响;hki为第k次测量数据向量的第i行数据,当i=1,2,···,n时,有p=1,2,···,r或q=1,2,···,n−r,最终可得: 满秩分解最小二乘法算法实现步骤为 1) 初始化式(13)中方差阵Pk、参数向量 θk;初始化上一时刻正交变换阵Vk−1为n阶单位阵;初始化满秩分解后方差阵等于Pk,满秩分解后参数向量等于 θk; 2) 通过测量值向量hk根据式(19)、(20)求取正交变换矩阵Vk; 3) 若Vk不等于Vk−1,根据式(18)求和,否则跳到4); 4) 根据式(13)求Pk+1;根据式(17)求和;根据式(16)由求,令等于 6) 循环2)~5)可实现参数在线辨识。 用于验证辨识算法的实验数据为三级海况下,一艘货船的自动舵数据记录仪从大连到新加坡航行过程中记录获得,系统采样频率为50 Hz。艏摇角速度r、舵角 δ和航向 ψ 数据如图1所示,角速度信号测量获得后,经过IIR低通滤波器滤除高频测量噪声后用于模型辨识。 图1 实验数据曲线Fig.1 Experiment data curves 分别采用LS、FFLS、MILS、LSSVM和FRDLS算法,基于图1中的实验数据对式(5)中的模型参数进行辨识,对比辨识结果,分析在辨识数据充分激励和欠激励工况下,辨识算法的辨识精度、收敛性和实时性。 MILS算法新息数选为10,FRDLS算法与FFLS辨识算法遗忘因子均为 β =0.99994,FRDLS算法阈值参数hs=1,LSSVM算法选择惩罚因子C为20,数据滑动窗口长度为500 s,K、T的初值选为0.2和250,扰动 δd初值为0,式(4)中归一化系数分别为 αr˙=25和 αr=50。对比5种辨识算法,参数辨识结果曲线如图2、3所示。 图2 K辨识结果曲线Fig.2 K-coefficient curves 图3 T辨识结果曲线Fig.3 T-coefficient curves 从图2、3可以看出,FFLS、MILS算法辨识K、T参数过程中,在200 s和3 000 s附近均出现参数发散,LSSVM算法数据滑动窗口进入1 200秒前后的船舶两次转向数据段时,K、T参数辨识收敛,滑动窗口进入1 800s之后航向保持数据段,辨识参数开始发散;FRDLS算法辨识K、T参数和扰动过程相对平稳,在船舶转向数据段和长时间航向保持数据段均未出现参数发散。辨识算法引入满秩分解后提高了遗忘因子最小二乘法参数辨识过程的鲁棒性。参数辨识结果见表1。 表1 参数辨识结果Table 1 Parameters identification results 为了对比上述算法辨识船舶航向模型参数的精度,可以将图2~图4中参数辨识结果代入式(3)中,以舵角数据为输入,对式(3)微分方程进行求解,从而预报船舶艏摇角速度。将预报结果与实验数据作差,可得到预报误差: 图4 δd辨识结果曲线Fig.4 δd-coefficient curves 式中ri和rip分别为第i时刻航向角速度测量值和预报值。预报误差越小,则辨识精度越高。为了保证航向角速度预报精度,此处采用四阶龙格库塔法求解航向模型微分方程。 式中:x=[rψ]T;f(x,t)=[(−r+Kδ )/Tr]T;Ts为系统采样周期,此处取Ts=0.02s。角速度预报曲线和预报误差曲线如图5、6。 图5 角速度预报曲线Fig.5 Yaw prediction curve 图5为航向模型参数辨识结果预报航向角速度曲线和实验测量角速度曲线。图6中给出了参数辨识结果角速度预报误差。从0~600 s预报误差曲线对比可知,FRDLS、MILS、FFLS相比于LS、LSSVM算法预报误差下降更快,有更快的辨识收敛速度。为了定量描述参数辨识精度,采用状态预报均方根误差(root mean square error,RMSE)作为航向模型辨识结果的精度指标,可根据式(23)求航向角速度预报均方根误差。 图6 角速度预报误差曲线Fig.6 Yaw prediction error curve 式中ei为式(21)中第i组数据航向角速度预报误差,角速度预报误差结果和辨识过程收敛性见表2。 表2 角速度预报误差Table 2 Yaw prediction error 根据表2,FFLS相比于LS算法,引入遗忘因子后参数辨识精度有所提高,同时导致辨识过程产生了发散现象;FRDLS算法引入满秩分解后,提升了FFLS算法辨识精度的同时,消除了辨识过程中的发散,说明遗忘因子和满秩分解两种新息处理方式相结合具有合理性。LSSVM算法在1 800 s后发散部分较多,对应的预报均方根误差结果为 94 943°·s−1,FRDLS 算法在 1 800 s后未出现参数发散现象,说明了FRDLS算法在数据欠激励、环境扰动工况下具有更好的收敛性。 辨识船舶航向模型参数的过程中,使用了179 996组测量数据对参数估计结果进行了更新,采用Qt软件C++编程语言,在window10系统下记录了FFLS、MILS、LSSVM和 FRDLS算法每次使用测量数据从计算数据向量到参数辨识值更新的时间,得到算法单次循环耗时曲线如图7所示。 图7 算法单次循环耗时曲线Fig.7 Algorithm time consumption for a single loop 算法单次循环最大耗时和平均耗时见表3。从算法耗时统计结果可知,FRDLS算法单次循环平均耗时为27.39 μ s,远小于LSSVM算法,耗时介于FFLS算法和MILS算法之间。由于满秩分解过程会额外消耗算法单次循环时间,牺牲了FRDLS算法部分实时性,以提升收敛性,耗时为FFLS算法的3倍左右,实时性在可接受范围以内。 表3 算法单次循环耗时Table 3 Algorithm time consumption for a single loop 本文针对数据欠激励受扰动系统参数在线辨识算法实时性、参数收敛性和辨识精度难以同时保证的问题,提出了一种满秩分解最小二乘算法,并使用该算法对长时间数据欠激励和海洋环境扰动工况下的船舶航向运动模型参数进行辨识。辨识结果表明,存在数据欠激励时,该算法能抑参数发散,并获得更高的辨识精度。且改进后的算法仍然计算量小、实现简单、实时性强、通用性好,具有较高实用价值,为实现准确稳定的航向自适应控制和欠驱动船自动靠泊奠定了基础。





3 实验验证

3.1 船舶航向模型参数辨识


3.2 船舶运动预报


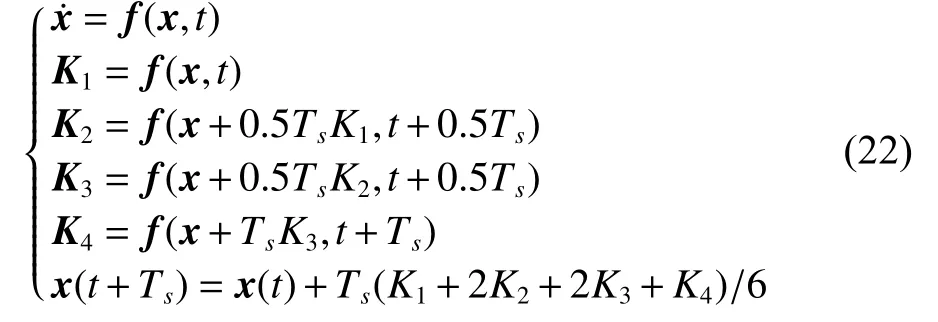



3.3 算法实时性分析

4 结束语
