信贷资产证券化的模糊随机定价模型*
2022-02-17张锦伦
张锦伦,张 勇
(吉首大学数学与统计学院,湖南 吉首 416000)
近年来,信贷资产证券化(Asset-Backed Securities,ABS)因具有盘活存量、扩宽债券市场广度、促进经济结构调整等积极功效,在政策上得到了我国金融管理体系的大力支持.在信贷资产支持证券定价研究方面,学者主要通过对信贷资产支持证券资产池未来现金流的大小和分布的预测,来确定信贷资产支持证券的理论价格[1-4].主流的定价理论模型主要通过构造随机微分方程的形式描述资产价格的不确定变化[5].但实际上,由于市场波动和信息不对称、不充分等,金融市场的不确定性包含了模糊性与随机性两方面,且二者不能相互替代,因此单凭随机性难以全面刻画资产价格的变化过程[5-10].笔者考虑将模糊随机理论与传统的资产定价理论相结合,构造金融市场不确定性环境下的信贷资产支持证券定价模型,以期为投资者的交易决策提供理论借鉴.
1 信贷资产支持证券价值分析
ABS产品的价值取决于资产池未来现金流的大小,而资产池未来现金流因受贷方的还款行为影响而具有不确定性.还款人选择在利率较低时提前还款,并以当前市场利率再次融资的行为,会造成资产池回笼资金提前,信贷资产支持证券未来现金流减少.贷款人提前还款行为会导致信贷资产支持证券价格的不确定性,而是否提前偿还又取决于利率的变化,因此本研究将考虑基础资产的早偿特征,并构造不确定环境下的信贷资产支持证券定价模型.
1.1 传统随机环境下的信贷资产支持证券定价
是否提前还款关键在于当前利率与借贷利率的差异,当前利率小于借贷利率时,借款方有权提前还款,利率大于借贷利率时则不提前还款,这契合期权的内涵.因此,笔者将信贷资产支持证券的价格P1分2个部分进行讨论,一是纯债价格P0,二是提前还款行为隐含的提前还款期权价格.
(1)纯债价格.纯债价格是在不考虑提前还款的情况下普通债券的价格.价格的大小取决于折现因子的大小,即
其中:C为固定债券的利息;B为最后偿还的本金;d为贴现率;t为期初至利息支付日的时间;n为剩余到期日的年限.
(2)提前还款期权价格.Cox等[11]认为债券价格是利率的递减函数,当市场利率上涨时,信贷资产支持证券价格会下跌,贷款人不会选择提前还款;反之,贷款人提前还款.也就是说,投资者卖出了一份美式看涨期权给贷款人,贷款人选择提前还款,表示该看涨期权被执行.但因为美式看涨期权价格近似等于欧式看涨期权[12-13],且Black-Scholes期权定价相较于蒙特卡洛模拟、二叉树等方法的计算更简便,所以笔者考虑运用Black-Scholes期权定价公式对信贷资产支持证券所包含的提前还款期权进行定价,定价公式为
f=SBN(d1)-Xe-rTN(d2).
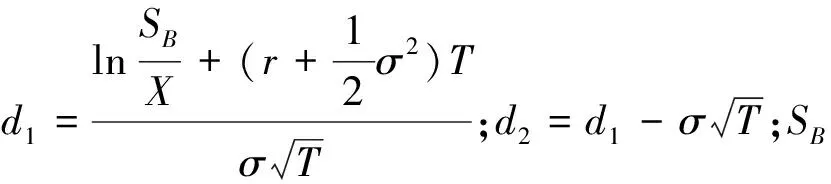
(3)信贷资产支持证券的价格.信贷资产支持证券的价格等于纯债价格与提前还款期权价格的差,即
(1)
(1)式给出了传统随机环境下的信贷资产支持证券定价,但由于传统的随机定价模型不能充分反映资产价格的不确定性,因此笔者尝试引入模糊理论[14],基于信贷资产支持证券的提前还款特征,构造模糊随机环境下的信贷资产支持证券定价模型.
1.2 模糊随机环境下的信贷资产支持证券定价
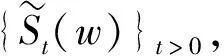
(2)

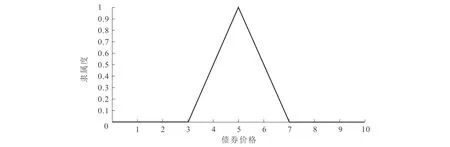
图1 隶属函数
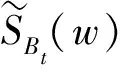
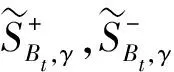
(3)
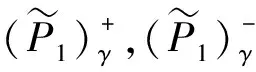
这里:

2 算法分析
假设对投资者来说,信贷资产支持证券有一参考价格P1,希望得到对应参考价格的隶属度γ,投资者再根据自身对隶属度的要求,确定是否接受信贷资产支持证券的价格.
在隶属度函数已知的情况下,求价格P1对应的隶属度,实际上就是求包含P1的最小模糊价格区间.由模糊数的性质可知,γ越大,价格P1的模糊区间越小,所以求解信贷资产支持证券价格对应的隶属度问题就转化为求解最大γ问题.最优化求解如下:
(4)
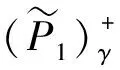
maxγ
s.t.P1≤g(γ),P1≥d(γ) 0≤γ≤1.
接下来分3种情况讨论信贷资产支持证券价格对应的隶属度:
(1)当d(1)≤P1≤g(1)时,资产支持证券价格P1对应的隶属度等于1.
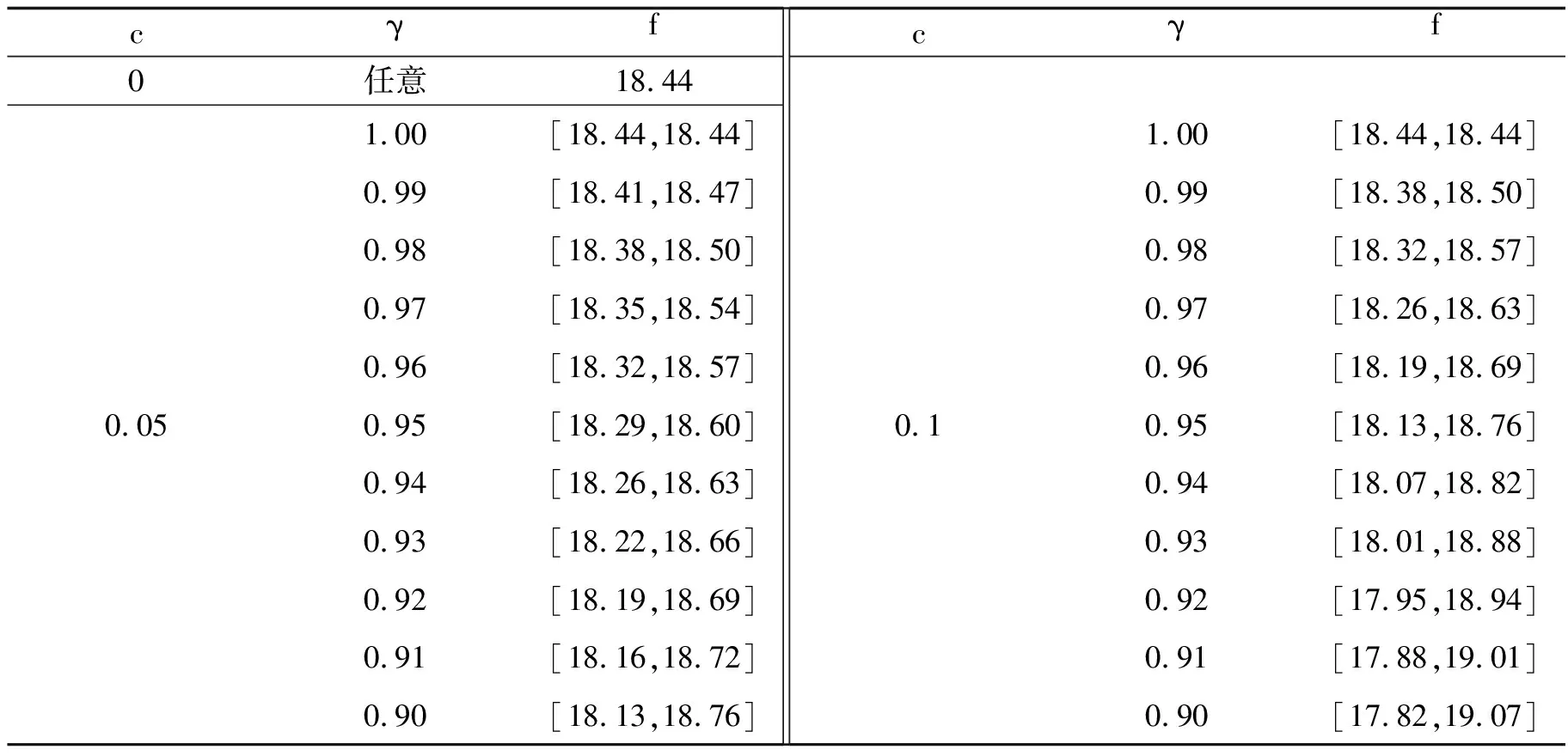
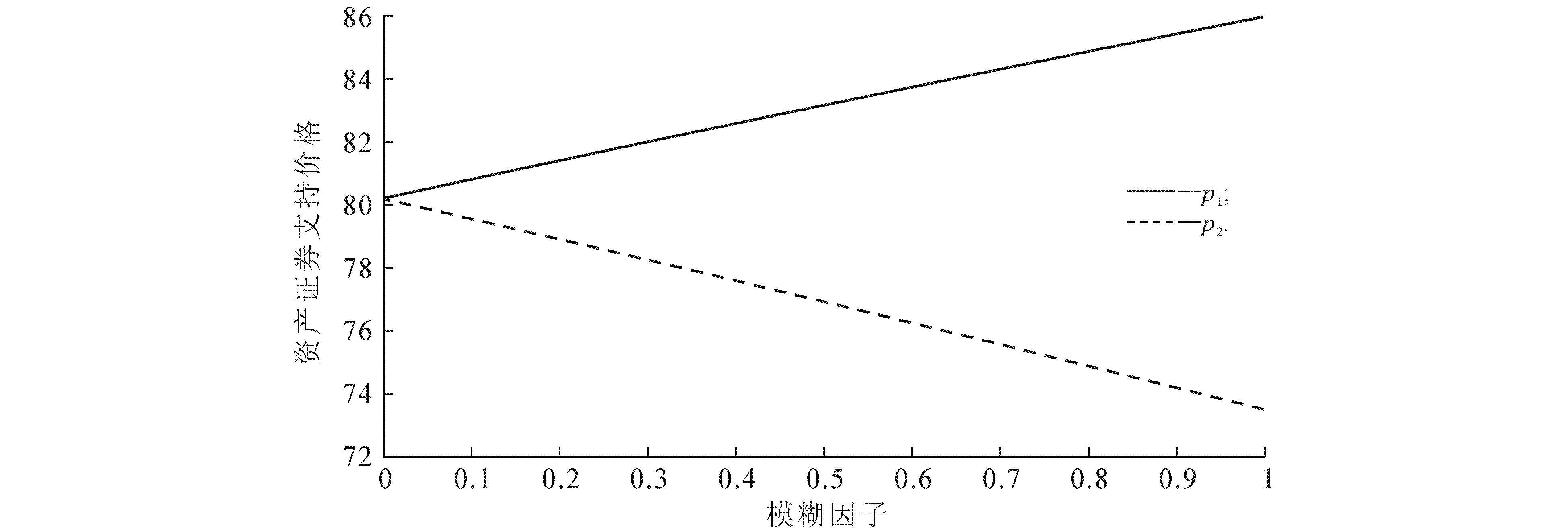
(2)当P1 maxγ s.t.P1≥d(γ) 0≤γ≤1. (3)当P1>g(1)时,有P1≥g(1)≥d(1)≥d(γ),即约束条件P1≥d(γ)必然成立.此时信贷资产支持证券价格的隶属度问题转化为如下最优化问题: maxγ s.t.P1≤g(γ) 0≤γ≤1. 以上最优化问题可采用对分算法[7]进行求解. 接下来结合数值算例验证信贷资产支持证券定价模型(3)的实用性. 信贷资产支持证券的价格包含普通债券的价格与提前还款期权价格.假设普通债券的面值为100元,票面利率为2.7%,到期期限为5年,每年付一次利息.提前还款期权的到期期限为2年,当前债券价格为102元,执行价格为103元,贴现率与无风险利率分别为0.03,0.02,波动率为0.3,模糊因子为0.05,0.1,那么纯债价格 取不同置信水平γ与模糊因子c,利用MATLAB软件计算得到信贷资产支持证券所包含的提前还款期权价格(表1). 表1 提前还款期权不同隶属度的价格区间 由表1可知,当c=0时,模糊数等于清晰数,信贷资产支持证券所包含的期权价格为18.44.此时模糊随机环境下的定价等于传统随机环境下的定价,这吻合传统随机环境下的定价是模糊随机环境下的定价特例的结论. 将纯债价格和提前还款期权价格(表1)代入模型(3),可得信贷资产支持证券价格(表2). 表2 信贷资产支持证券不同隶属度的价格区间 表3给出了模糊因子为0.1时不同信贷资产支持证券价格的隶属度.若此时信贷资产支持证券价格为80.73,投资者能够接受隶属度为0.911 76,则可以将80.73视为其投资决策的参考价格. 表3 不同信贷资产支持证券价格对应的隶属度 投资者进行投资决策的具体步骤如下: (ⅰ)投资者选择一个自己能够接受的隶属度水平. 为了进一步探究模糊参数c,γ的敏感性,笔者通过控制变量的方法展开稳健性分析.取隶属度为0.9,分析模糊因子对信贷资产支持证券价格的影响,结果如图2所示. 图2 模糊因子与信贷资产支持证券价格的关系 取模糊因子为0.1,其他参数不变,分析隶属度与信贷资产支持证券价格的关系,结果如图3所示. 图3 隶属度与信贷资产支持证券价格的关系 本研究考虑了信贷资产支持证券的基础资产(贷款)可能存在的提前还款风险,构建了受提前还款行为影响的信贷资产支持证券定价模型.为了使模型更能适应不确定的市场环境,笔者引入模糊理论,构建了模糊随机环境下信贷资产支持证券定价模型,并通过算法分析、数值算例对其进行了验证,得到以下结论: (1)通过建立理论模型发现,模糊随机环境下的信贷资产支持证券定价模型是传统随机定价模型的推广,且相对于传统定价模型,模糊随机环境下的定价具有更一般的意义,适用性更广. (2)数值算例结果表明,对于投资者来说,模糊随机环境下的信贷资产支持证券定价相较于传统定价更具有灵活性,投资者选取其能够接受的置信水平,进而得出投资者投资决策价格的区间,并通过比较市场价格与模糊价格的大小确定交易策略. (3)通过静态分析发现,风险承担能力较大的投资者相较于风险承担能力较小的投资者,投资决策的灵活性更大,承受市场不确定性的能力更强. 笔者研究了基于提前还款问题的信贷资产支持证券模糊随机定价,发现模糊随机定价模型是传统定价模型的推广,能更好地适用于信息不对称、不确定的市场环境.本研究基于Black-Scholes期权定价模型下的模糊定价是一种近似定价,而模型参数的主观性会对信贷资产支持证券定价的结果产生影响,因此更准确的定价方法还有待后续探讨.3 数值算例与比较静态分析
3.1 数值算例

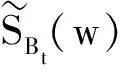

3.2 比较静态分析



4 结语
