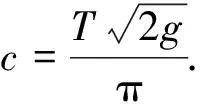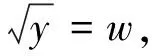降线问题的阿贝尔积分方程的求解*
2022-02-17邢家省
邢家省
(1.北京航空航天大学数学科学学院,北京 100191;2.北京航空航天大学“数学、信息与行为”教育部重点实验室,北京 100191)
等时降线问题[1-4]是历史上著名的问题.1673年,惠更斯利用几何方法证明了等时降线的解为一条倒摆线.1690年,雅各布·伯努利发表了关于等降线的解答,导出了等时降线问题的解是一条倒摆线.拉格朗日和欧拉也运用解析方法解出了等时降线问题.1823年,阿贝尔将降线问题转化为一个积分方程的求解问题,从此引起了人们对积分方程的关注.笔者拟对等时降线的积分方程给出严密的求解方法,对等时降线的微分方程给出自然的解法,以期形成一套完整的方法体系,便于引用和传播.
1 质点沿光滑轨道下降所需时间的公式
建立xOy坐标系,Ox轴正向水平向右,Oy轴正向竖直向上.设A点坐标为(x1,y1),B点坐标为(x2,y2),x1 或者为 设曲线L的最低点在Ox轴上,质点在曲线L上从高度为h的点处静止开始下降到最低点处所需时间[1-4]为 (1) (1)式是由阿贝尔导出的积分方程,由此引起了学者对阿贝尔积分方程求解问题的兴趣[1-9]. (2) 积分方程问题[1,4]是给定函数T(h),寻找函数φ(y),使得满足(2)式. 考虑如下积分方程问题: (3) 其中0<α<1.阿贝尔运用拉普拉斯变换[7-13]给出了(3)式的求解方法.将拉普拉斯变换记为 引理1[7]设常数m>-1,则有 引理2[7]设常数0<α<1,则有 对(3)式两边作拉普拉斯变换,利用拉普拉斯变换的卷积性质可得 L(φ)(s)L(t-α)(s)=L(f)(s). 利用广义积分的计算方法[14-20]可得 于是 利用 由拉普拉斯变换的性质可得 (4) (4)式即为(3)式的求解公式,将(3)式的解写为(4)式的形式可便于使用. 由余元公式[7-13]可得 (5) 现考虑(2)式的求解问题.当T(h)=T(T为常数),即等时降线情形时,利用(5)式可得 于是 从而得到等时降线情形时的微分方程 (6) 进一步对微分方程(6)进行求解,可知等时降线是一条倒摆线.这里给出的解法是阿贝尔关于等时降线问题的求解方法[1-9]. 设常数H>0.因为实际降线问题是从有限高度下落的,所以降线问题可归结为如下的积分方程和微分方程问题[1-4]: (7) (8) 积分方程问题[1,4]是给定函数T(h),寻找函数φ(y),使得满足(7)式. 引理3[2,9]设a 证明 证毕. 引理4[2,9]设p(x)∈C1[a,b],且p(x)在[a,b]上严格单调递增,0<α<1,则有 证明 证毕. 考虑积分方程 (9) 其中0<α<1. 引理5[2,9]设p(x)∈C1[a,b],且p(x)在[a,b]上严格单调递增,0<α<1,f(x)∈C[a,b],则(9)式的解为 证明利用(9)式及引理4,可得 于是 证毕. 利用引理5可得如下结论: 引理7[2,9]设φ(x)在(0,H]上连续可积,令 则有 现对等时降线的积分方程进行求解,即T(h)为常数T时进行求解.此时积分方程为 (10) 对(8)式利用定理3,可得 于是 (11) (11)式就是(10)式的解式. 在等时降线情况下,利用(10)式的解式(11),得到如下常微分方程: (12) 令t=2θ,则有 这正是倒摆线的方程形式,由此可知等时降线是倒摆线.Oprea[21]和邢家省等[22]对倒摆线具有等时性给出了计算验证.2 阿贝尔积分方程的拉普拉斯变换求解
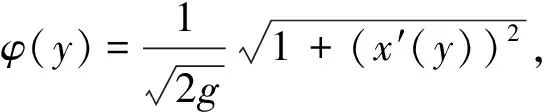

3 质点从有限高度下落的降线问题的阿贝尔积分方程
4 有限区间上的积分方程求解
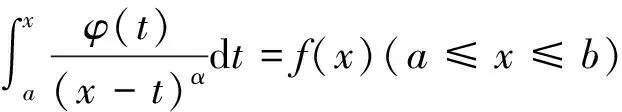
5 等时降线的阿贝积分方程求解
6 等时降线是倒摆线的证明