基于改进灰色模型的电力负荷可靠性预测系统设计与实现
2022-02-17钟立华罗婷
钟立华,罗婷
(广东电网有限责任公司东莞供电局,广东东莞 523000)
随着电力市场化的不断推进,合理的电力规划能够较大地增加社会效益与经济效益,而电力负荷预测可为电力系统的规划运行与调度安排提供有力的决策支撑[1-2]。准确的电力负荷预测能够有效保障电力系统的安全、稳定运行,对我国智能电网建设具有重要意义[3-4]。
由于电力负荷数据具有非线性、波动性等特征,传统方法难以对电力负荷进行准确的预测[5-6]。随着智能算法的发展,如遗传算法[7]、小波变换[8]和人工神经网络[9]等多种算法被引入到电力负荷预测领域。其中,灰色模型由于具有样本容量需求量小、运算速度快的优势,在电力负荷预测领域的应用中取得了较优的效果,并衍生出诸多改进模型[10-12]。该文在灰色模型基础上考虑气象影响因素,引入残差修正法与马尔科夫法对其进行改进,进而设计得到基于改进灰色模型的电力负荷可靠性预测系统。将其应用于实际电力负荷预测,取得了较优的效果。
1 改进灰色模型
1.1 灰色模型建模
灰色模型是一种无需大容量样本、运算速度较快的预测模型。其中,模型GM(1,1)是GM(1,n)的特殊情况,通常只含有单一变量,主要由一阶微分方程组成,可以根据历史数据有效预测未来数据,其建模过程如下[13-14]。
数据初始序列定义,如式(1)所示:

通过对式(1)进行一阶累加,可得式(2):
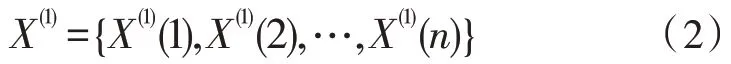
式(2)中:
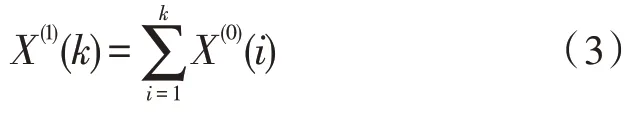
因此可以列出微分方程,如式(4)所示:

式(4)中,c表示发展系数,代表初始数列增速,ξ表示模型的作用参量,代表数据序列的变化情况。通过采用最小二乘法可求解得到模型参数c和ξ,如式(5)所示:
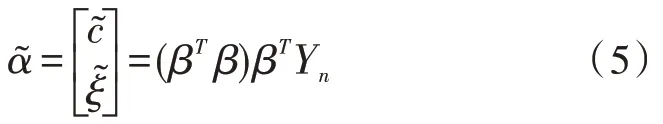
式(5)中β的计算如下所示:
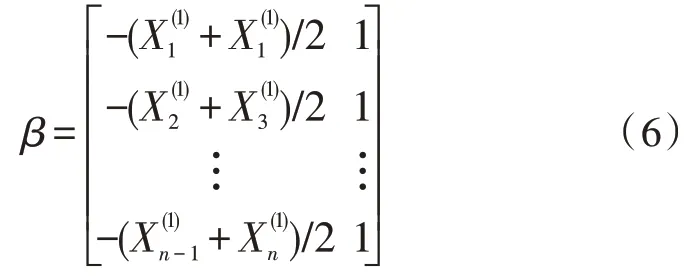
通过求解得到相应基于累加数据序列的GM(1,1)预测模型,如下式所示:
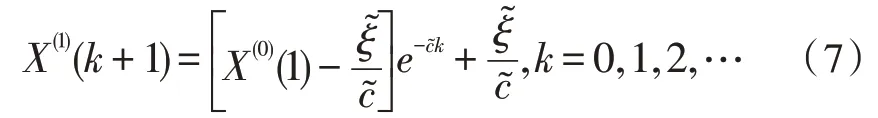
对式(7)进行累减可以还原得到初始数据序列对应的灰色预测模型,如下所示:
普通的灰色模型将初始的数据序列进行相应的生成处理,从而确定其波动规律。由此得到具有规律性的数据序列,根据生成的数据序列构建相应的微分方程模型,预测数据的未来变动趋势。
1.2 气象因素
气象因素对于电力负荷的短期预测具有重要影响,其中,温湿度会直接影响电力负荷曲线的波动情况[15-16]。因此,该文将温度和湿度进行量化,得到了气象影响因子,计算公式如下所示:
其中,λ是(0,1)中的随机常数,表示气象影响因子的影响指数。调节λ的大小可以控制量化后的温度参量T(t)与湿度参量H(t)的影响程度。λ值越大,表明该因素对负荷的影响越大。
在预测电力负荷前,应当首先还原在剔除气象因素影响条件下的历史电力负荷数据序列,如式(10)所示:
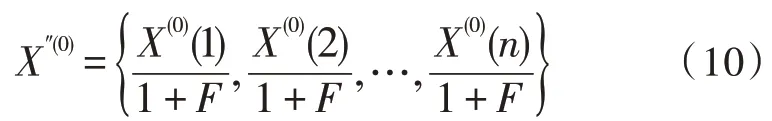
利用灰色模型可以得到电力负荷预测值(k=1,2,…,n),在考虑气象因素的条件下引入气象影响因子,则预测值为如式(11)所示:

1.3 残差-马尔科夫修正模型
灰色模型的实质是对呈指数增长的数据序列进行拟合,因此当数据序列呈现指数增长特征时,灰色模型能够较好地预测未来的数据序列。然而当数据序列不具有指数增长特征或是波动性较高时,灰色模型预测的结果通常难以满足准确性的需要。因此可以引入残差序列修正灰色模型,从而有效提升模型的预测准确性。对于式(1)中的数据初始序列采用GM(1,1)得到预测值,由此可以计算残差序列,如式(12)所示:

其中:
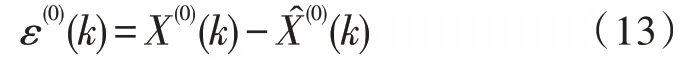
若有某个整数k0符合以下条件:1)∀k≥k0,ε(0)(k)符号相同;2)n-k0≥4,则|ε(0)(k0)|,|ε(0)(k0+1)|,…,|ε(0)(n)|表示建模的残差尾段。采用GM(1,1)对其进行相应的预测即可得到残差尾段的模型预测值,即其中:

利用对修正即可得到预测值,如式(15)所示:

其中:

式(15)中正负号的选取应当与残差尾段保持一致。为了使残差的正负号保证一致性,通常需要执行平移操作,使得预测产生偏差。因此引入马尔科夫方法对其进行修正,预测残差的正负号,则搭建残差-马尔科夫模型的流程如下所示:
1)利用式(13)计算得到残差数据序列ε(0)(k)。
2)基于GM(1,1)构建残差数据序列ε(0)(k)的预测模型,根据式(7)求解得到相应的预测数据序列ε̂(0)(k),如下所示:

3)依照残差正负号划分为两种不同状态从而表征某时刻残差的正负情况,残差符号为正时将状态设定为1;反之,则设定为状态2。由此可以得出,其转移概率矩阵M,如式(18)所示:


由于残差的符号可以用两种状态进行表征,因此引入函数sgn(k)改写残差值公式,如式(20)所示:

其中:
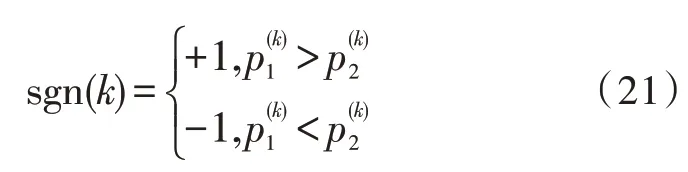
利用式(20)修正GM(1,1)模型预测值,可得到式(22):

普通灰色模型在预测时随着时间变化会受到某些因素的随机干扰,越往后预测准确性越低,因此通常仅预测一个最近数据。为了能够预测更多的数据,在应用修正模型时,引入等维信息补全法。持续将新的预测值增添到数据序列中,并删除序列早期的数据,然后再进行预测,如此不断往复,即可实现连续预测。由此可以得到基于改进灰色模型的电力负荷预测方法流程,如图1 所示。

图1 基于改进灰色模型的电力负荷预测方法流程
2 电力负荷可靠性预测系统设计
2.1 系统总体设计
该文提出的电力负荷可靠性预测系统属于能效管理系统的应用功能,可实现在Windows 7 操作系统上的侦查和运行。其中,算法实现工具选择Matlab 2018b,开发语言选择Java 语言,数据库管理软件选择MySQL。电力负荷可靠性预测系统开发流程图,如图2 所示。
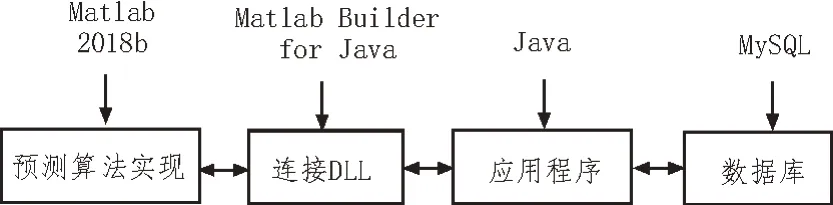
图2 电力负荷可靠性预测系统开发流程图
2.2 系统功能设计和实现
该文设计的系统主要有4 个功能单元,系统总体功能结构如图3 所示。
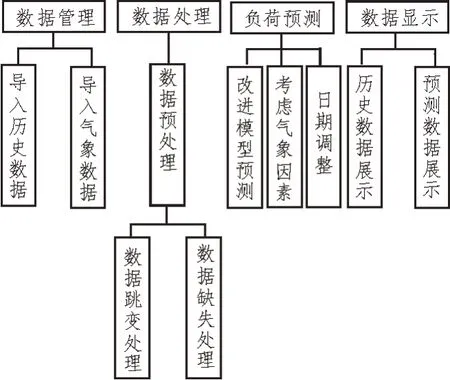
图3 系统功能结构
1)数据管理。这一系统单元的功能是负责导入电力负荷历史数据与气象数据,前者可通过数据采集系统内部具有的存储数据库执行导入操作,后者可利用WebService 技术从网络执行导入操作。
2)数据处理。这一系统单元的功能主要是实现对于电力负荷历史数据预测前的预处理。由于电力负荷预测主要采用的是初始数据序列,预测准确度受初始数据序列影响较大。
3)负荷预测。该单元所具有的预测功能是系统的核心功能,基于改进灰色模型,同时考虑气象因素的影响,通过编程实现电力负荷的定时自动预测。
4)数据输出。这一系统单元的功能是将电力负荷历史数据与预测得到的电力负荷数据进行展示,通过执行调用指令可在能效管理系统的对应页面查看电力负荷预测数据序列曲线与实时数据序列曲线的对比图,也可以查看某日电力负荷数据曲线图。
3 系统测试
为了验证所设计负荷预测系统的正确性与可靠性,测试了系统的核心功能,即负荷预测功能。选择某地2019 年10 月21 日00:00~23:00的电力负荷数据进行预测。其中每个电力负荷数据在时间上相隔1 h,当日最高气温为19 ℃,最低气温为8 ℃,湿度为80%RH,气候条件较为适宜。系统预测负荷曲线与实际负荷曲线对比结果,如图4 所示。两者误差,如表1 所示。

图4 系统预测负荷与实际负荷对比
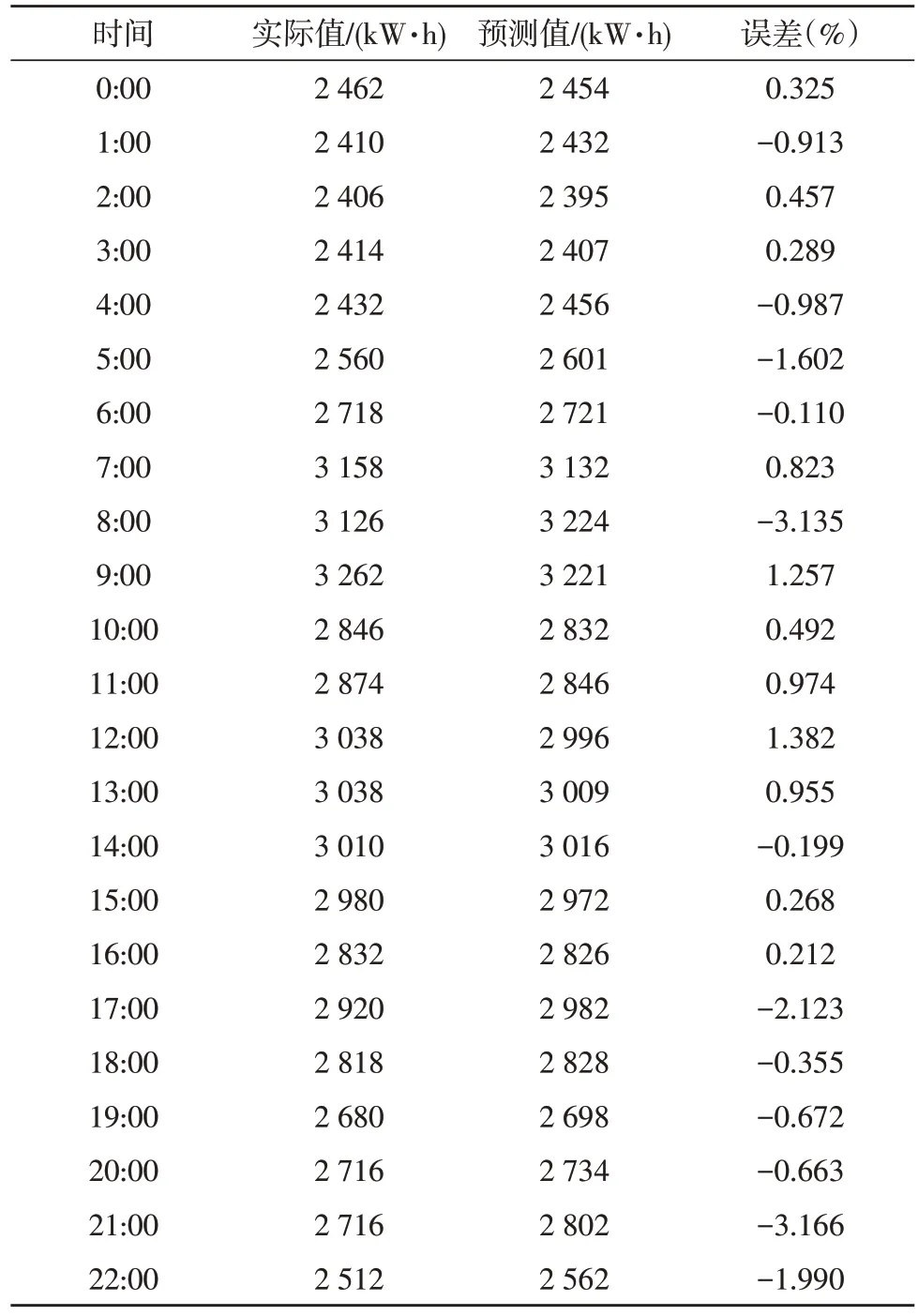
表1 预测误差
由图4 与表1 可以看出,测试当日的电力负荷曲线大致波动范围在2 200~3 300 kW·h 之间,白天电力负荷较高,夜晚电力负荷较低,且电力负荷曲线波动情况较为稳定,符合正常工作日的电力负荷波动情况。当系统对电力负荷进行预测时,预测的平均精度为99.575%,相对误差最大为3.166%,相对误差最小为0.110%。经过分析可以看出,该系统预测的工作日电力负荷曲线与实际电力负荷曲线近似,且误差较小。系统功能测试结果表明,在较为适宜的气候湿度与初始数据序列波动性低的条件下,文中的负荷预测系统具有较高的预测精度,且预测系统的可靠性高,能够较好地满足实用性要求。
4 结论
该文提出了一种基于改进灰色模型的电力负荷可靠性预测系统。在考虑气象因素的基础上,引入残差-马尔科夫修正模型对灰色模型进行改进,得到相应的电力负荷预测方法,进而设计了系统数据库结构与功能单元,最终实现了预测系统的总体设计。通过系统测试可以看出,文中设计的预测系统精度较高,且可靠性强。在电力负荷预测方面具有较好的应用前景,可为电力系统经济运行的相关研究提供一定的参考价值。
