双锥对撞点火机制2020 年冬季实验中的瑞利-泰勒不稳定性分析*

方可 张喆 李玉同3)4) 张杰

1)(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

2)(中国科学院大学物理科学学院,北京 100049)

3)(松山湖材料实验室,东莞 523808)

4)(上海交通大学IFSA 协同创新中心,上海 200240)

5)(上海交通大学物理与天文学院,上海 200240)

直接驱动激光聚变通过整形后的纳秒脉冲激光辐照氘氚(DT)球壳靶,经球对称压缩加速后,在中心转滞获得高温等离子体热斑,实现聚变点火.在球壳靶受到压缩和加速过程中等离子体界面的流体力学不稳定性,特别是瑞利-泰勒不稳定性的增长有可能会对压缩壳层造成破坏,导致点火的失败.本文通过理论解析和数值模拟,对基于Zhang 等提出的双锥对撞点火方案(2020 Philos.Trans.A Math.Phys.Eng.Sci. 378 20200015)在2020 年冬季实验条件下的流体力学不稳定性增长进行了分析.结果显示理论模型与一维数值模拟中对整体压缩和加速过程的描述基本一致,在当前的近等熵波形下金锥中的壳层靶实现了低熵压缩,同时瑞利-泰勒不稳定性增长导致的最危险时刻扰动振幅和壳层厚度比可以达到约0.25,壳层依然处于安全状态,但当初始壳层表面扰动均方根振幅大于22 nm 时,则可能出现壳层的破裂.因此,未来实验中的靶设计与驱动激光脉冲波形设计中可以通过增加靶壳层厚度、提高预脉冲强度、减小靶表面的粗糙度和提高激光辐照的匀滑度等方式来抑制不稳定性增长.

1 引言

自1972 年Nuckolls 提出用激光烧蚀靶丸表面产生球对称内爆压缩燃料实现中心点火可控核聚变的概念以来,出现了不少基于直接或间接驱动路线的激光聚变点火方案[1-4],近年来其中一些方案已经实现了较高水平的聚变中子产额[5-7].在这些点火方案中,流体力学不稳定性的发展,包括冲击波阶段的Richtmyer-Meshkov Instability (RMI)增长和压缩加速阶段的瑞利-泰勒不稳定性(RTI)增长,都对燃料压缩所能达到的密度和最终的中子产额有很大影响[8-13].围绕激光聚变中的流体力学不稳定性增长,数十年来已经有大量的理论、模拟和实验研究[14-17].壳层飞行过程中的加速度和质量烧蚀速率将会对RTI 增长有决定性的影响,同时烧蚀面附近的密度梯度和质量烧蚀速度也能抑制短波长RTI 的增长[9-13,18].

双锥对撞点火方案利用优化设计的驱动激光,在金锥内对球壳燃料进行球形内爆形成等熵压缩,使燃料达到极高的密度与速度,并从锥口喷出,与对向锥口喷出的等离子体对撞达到密度与温度的提升,形成等容构型热斑[19].金锥壁可以与轴向烧蚀压结合在一起对燃料进行球对称压缩,并使照射进金锥的激光能量得到充分利用,对撞则可以在相对较低的驱动能量下得到更高的燃料密度和温度.高功率皮秒激光点火脉冲聚焦在对撞等离子体侧面,产生的超热电子在外加磁场的引导下进入等离子体沉积能量,进一步加热燃料达到点火条件.双锥对撞点火方案要求燃料在锥内压缩过程中达到较高的密度和速度,并保持完整性和对称性.流体力学不稳定性增长则有可能破坏壳层的完整性和均匀性导致点火失败[20],因此对锥内压缩和加速阶段流体不稳定性增长的理论计算和数值模拟是非常必要的.

本文基于冲击波、壳层加速和烧蚀RTI 增长的解析公式构建理论计算模型[10,11,18],描述双锥对撞压缩和加速阶段的近等熵压缩波形下的燃料压缩和加速过程,并与一维流体模拟程序MULTI 1D[21]结果对比,得到随时间变化的壳层加速度和烧蚀层状态.流体力学不稳定性分析表明,在当前方案下的RTI 增长率依然较大,因此需要在壳层靶设计和驱动激光波形设计时,进行统筹考虑.

2 双锥对撞方案冬季实验中的压缩和加速过程

2.1 靶形和激光波形设置

本文理论计算模型参考2020 年进行的冬季实验里双锥对撞点火方案[19]中的靶构型,将塑料材质的烧蚀壳层置于锥靶当中,两锥口正对放置,相距约 100 μm,如图1(a)所示.锥顶半开角为 50°,烧蚀物壳层材料为聚乙烯(C8H8),厚度约 50 μm,外径约 500 μm,暂时没有使用氘氚(DT)材料.激光为3ω纳秒激光,波形为如图1(b)所示的近等熵波形[19].

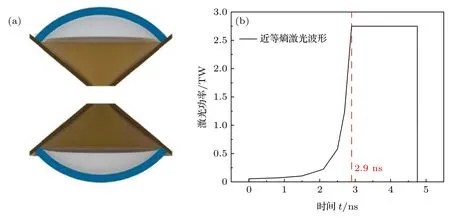
图1 理论模型中的双锥靶和近等熵激光波形 (a)双锥靶示意图;(b)近等熵激光波形Fig.1.Double cone targets and quasi-isentropic waveform in the theoretical model:(a)Diagram of the double targets;(b)quasi-isentropic waveform.

激光开始时刻功率为 54.5×109W,初始光强约 1.2×1013W/cm2.随后激光功率和强度逐渐上升,为壳层提供近等熵压缩,使壳层达到较高的密度.脉冲在 2.9 ns 时刻达到峰值功率并持续 1.85 ns,这段时间内激光脉冲将推动壳层向锥口加速飞行,使壳层以较高的速度喷出,从而在对撞后尽量接近热斑点火条件[22].但过高的速度容易导致壳层在加速过程中因RTI 增长产生的气泡而破裂,所以激光波形和靶型的设计同流体力学不稳定性增长紧密相关.

2.2 理论模型中的烧蚀压

双锥对撞点火方案中激光波长为 0.351 μm,强度在 1013—1015W/cm2之间变化,激光能量主要通过逆轫致吸收被烧蚀层材料吸收.再考虑到锥内壳层的球面结构,可以采用Mora (1982)的烧蚀压公式[18,23,24]

式中,Pa是激光加热靶丸表面材料产生的烧蚀压;是单位面积质量烧蚀速度;IL是激光强度,单位为 1013W/cm2;λL是激光波长,单位为 μm;rf≈0.38 mm 为激光叠合后的焦斑半径.rf和IL随壳层的飞行会有变化,考虑到飞行过程中金锥壁暴露出来导致传导层同时覆盖锥内球壳和金锥壁,球壳烧蚀面面积减少而激光聚焦面积几乎不变这一过程,采用一种简化的理论计算模型,如图2 所示.

图2 简化理论模型示意图Fig.2.Sketch of the simplified theoretical model.

第一处简化处理是,假设激光能量被吸收处的面积在压缩过程中始终不变,这一假设和流体计算程序FLAHS 2D 的模拟结果基本符合.第二处简化处理中考虑到烧蚀面即实际的壳层质量损失面是一个球锥面:

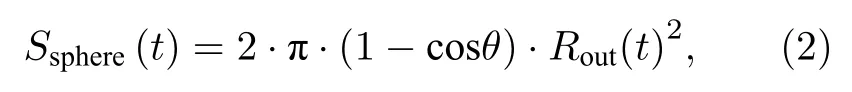
式中,θ为锥顶半开角,Rout为壳层外表面.当后期壳层收缩变小后,临界密度面竖直方向投影中的一部分并不对应烧蚀壳层,而是金锥壁,壳层实际烧蚀面处的质量烧蚀速率根据质量守恒公式计算:

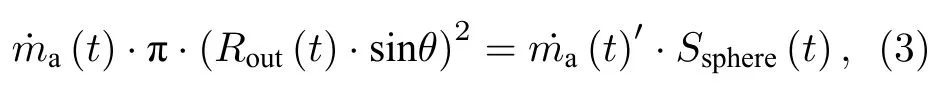
这会影响到RTI 增长过程中的烧蚀致稳效果.

2.3 冲击波的产生和压缩

激光产生烧蚀压的同时会引起冲击波压缩和加热靶丸,并导致熵增,影响密度和烧蚀速度.冲击波的传播过程由于戈尼奥关系式描述[25]:

式中,ρ1,P1,u1和ρ2,P2,u2分别代表冲击波波前和波后物质的密度、压力和物质飞行速度;us代表冲击波波面传播速度;γ为理想气体的绝热系数.计算冲击波时P2=Pa.根据冲击波物性实验结果[25]可以直接得出理论模型中初始时刻的冲击波波后密度ρ2≈3.15 g/cm3,对应等效初始压力P1≈0.27 Mbar (1 bar=105Pa).激光功率上升产生一系列相互叠加的冲击波引起密度和熵增加,这里引入物质等熵参数α[26]随冲击波和物质的压力密度之比而变化的关系:

式中,等熵参数α和α0分别代表特定冲击波的波后和波前物质等熵参数,冲击波通过后物质压力和密度的 5/3 次方之比将会增大,导致波后物质等熵参数增大.壳层初始时刻等熵参数α0=1.0,当第一个冲击波通过后壳层等熵参数α≈1.758,2.9 ns激光强度达到最大值后壳层外表面等熵参数α≈2.108,密度达到 17.59 g/cm3.

冲击波引起的不同时刻壳层空间密度分布如图3.图3(b)中解析模型冲击波突破时刻为t=2.06 ns,最大密度为 5.35 g/cm3,与流体模拟程序MULTI 1D[21]中t=2.30 ns,ρmax=5.03 g/cm3基本一致,但后续压缩中解析模型密度高出模拟结果2 倍,原因是解析模型没有考虑稀疏效应带来的密度梯度变化.

图3 冲击波压缩阶段不同时刻空间密度分布 (a)1.0 ns 时刻空间密度分布;(b)2.06 ns 时刻空间密度分布;(c)2.5 ns 时刻空间密度分布;(d)2.9 ns 时刻空间密度分布Fig.3.Density profile at different time in shock wave compress stage:(a)Density profile at 1.0 ns;(b)density profile at 2.06 ns;(c)density profile at 2.5 ns;(d)density profile at 2.9 ns.

对于瑞利-泰勒不稳定性增长,最重要的物理量是加速度、密度梯度和质量烧蚀速度.理论和模拟中的壳层运动轨迹和加速度基本一致,烧蚀面密度梯度则由模拟程序计算.

2.4 加速阶段

激光达到最大功率后停止产生冲击波,燃料的熵不再增加,壳层进入加速阶段.这个阶段壳层的速度uimp由火箭方程描述[18]:

式中,uex是排出速度,M0是初始壳层质量,M1是壳层的剩余质量.对于双锥对撞点火方案,考虑到球壳烧蚀面和对应的激光吸收面随时间不断缩小,有

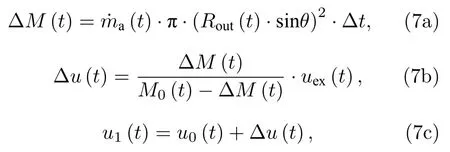
式中,u0,u1分别是t时刻计算火箭效应之前和之后的壳层速度,Δu是速度改变量.加速阶段壳层密度维持不变,并由等熵参数和费米简并压之间的关系计算[18]:

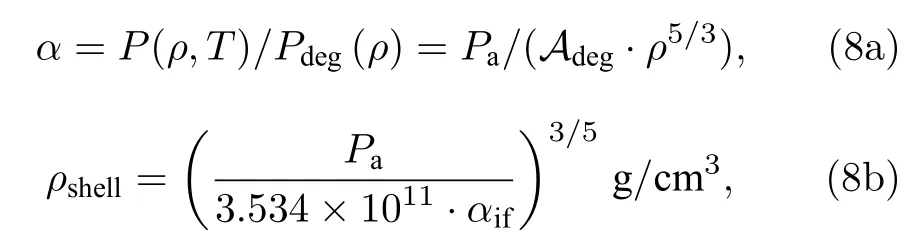
式中,Pdeg(ρ)代表燃料壳层在一定密度下的费米兼并压,常数项Adeg=3.534×105J·cm2·g-5/3.飞行等熵参数αif=2.1 ,ρshell=3.6 g/cm3,密度下降是由于壳层经历等熵稀疏过程.解析模型通过(6)式计算出内表面飞行速度,而外表面的位置、速度和加速度根据壳层密度和剩余质量得到:

由(6)—(9)式描述的理论模型和MULTI 1D 计算得到的壳层飞行轨迹如图4 所示.

图4 壳层飞行轨迹和加速过程壳层厚度 (a)壳层内外表面飞行轨迹;(b)加速过程壳层厚度变化Fig.4.Trajectories of the shell and shell thickness during the acceleration-phase:(a)Trajectories of inside and outside surface of the shell;(b)variation of the shell thickness during the acceleration-phase.

解析计算和流体模拟中的壳层飞行轨迹基本重合,主要差别在于冲击波突破后内表面成为自由面,解析模型中则进行了简化,导致壳层密度和厚度存在跳变.加速飞行后期,由于向心收缩和燃料堆积,外表面开始减速,但内表面却继续加速.4.75 ns 激光结束时刻,解析模型中外表面Rout=228 μm,速度为 130 km/s ,内表面Rin=182 μm,速度为 199 km/s ,对应MULTI 1D 中Rout=229 μm,uout=125 km/s,Rin=190 μm,uin=177 km/s,理论和模拟对壳层飞行轨迹的描述接近.

2.5 等离子体碰撞的实验结果

在冬季实验中,利用Kirkpatrick-Baez (KB)显微镜[27,28]对锥口对撞等离子体自发光信号进行二维图像的时间分辨观测.KB 显微成像系统由4 组8 面柱面镜组合而成,在像面呈现4 行4 列共16 个均匀排列的像,并用分幅相机进行采集.视场中心处KB 显微镜的空间分辨率达到 10 μm ;分幅相机扫描脉宽为100 ps.图5 所示为典型发次的自发光信号强度随时间的演化.

图5 冬季实验对撞等离子体自发光信号强度变化Fig.5.Temporal evolution of self-emission signal of colliding plasma.

实验结果显示,信号在激光结束后1.0—1.1 ns附近开始迅速增强,来自于锥口物质前锋的对撞.在 1.4 ns 信号达到峰值强度并持续约 0.2 ns,随后信号强度迅速下降直至 1.8 ns .实验中单锥发次锥口喷出的等离子体则看不到自发光信号的突然增强现象,且信号强度很弱.

对撞等离子体的自发光强度反映了对撞过程的动力学行为,实验结果与理论计算、Multi 1D模拟的结果比较如表1 所列.从表1 可以看出,理论与模拟的结果和实验相比差异小于20%.在目前激光条件下,理论和模拟结果可以较好地重现实验结果.

表1 实验、理论和一维模拟中对撞等离子体自发光信号时间对比Table 1. Temporal comparison of self-emission signal of colliding plasma in experiment,theoretical model and 1D simulation.

3 流体力学不稳定性增长

3.1 初始表面扰动振幅和RMI 增长的处理

流体力学不稳定性增长的种子,即初始表面扰动振幅,取决于靶丸的制作精度和激光叠合产生的焦斑不均匀性,激光的影响更多地体现在长波长模式不均匀性上[29].由于目前缺乏对双锥对撞点火方案中靶丸表面初始扰动振幅的测量,所以解析模型中引用NIF 流体模拟设置的初始表面扰动振幅模式[14]:

式中l为表面扰动振幅的勒让德多项式模式l=2πR/λ,ζout(l)是壳层外表面上模式为l的初始扰动振幅.

理论模型中,冲击波阶段会产生RMI 增长,成为后续RTI 增长的种子扰动,但激光烧蚀下的RMI 增长需要考虑烧蚀效应和复杂的振荡过程[9],所以在计算RTI 增长前,将激光的印记作用和RMI增长导致的扰动均包含进初始扰动公式[10]中.当激波突破壳层后表面,壳层开始加速飞行,此时RMI 和RTI 同时存在,但RTI 呈指数增长远大于线性增长的RMI,所以这个阶段同最后的加速阶段一样,需要考虑RTI 增长带来的影响.

3.2 加速过程中的RTI 增长

随着壳层外表面开始加速,加速度方向和壳层密度梯度相反,体系处于高势能不稳定状态,初始表面扰动振幅开始增大.激光的烧蚀将会很大程度上消除短波长模式的表面扰动,动力学过压则会减弱振幅增长[29].烧蚀RTI 的线性增长由Takabe公式描述[10-12]:

式中,keff(t)=l/Rout(t)是有效波数,Lmin(t)是外表面附近的最小密度梯度,a(t)是壳层加速度,ua(t)=是烧蚀速度,(11a)式中第二项烧蚀项代表了烧蚀致稳作用.对直接驱动的CH烧蚀材料系数取值[11]α=1,β=1.7.在第2 节的理论模型中已经得到加速度、密度和烧蚀速度,对于固定的扰动模式l,随着壳层的收缩有效波数keff会变大.还有1 个需要确定的量是最小表面密度梯度标长[12]Lmin=min|ρ/∇ρ|,代表密度梯度对不稳定性增长的抑制作用,可以从MULTI 1D 流体模拟中得到,其变化如图6 所示.

图6 壳层外表面最小密度梯度标长LminFig.6.The minimum density-gradient scale length on the outside surface of the shell.

在2.9 ns 之前,Lmin呈现缓慢下降趋势,在2.9 ns之后,Lmin随时间逐渐上升,可以近似拟合为

当扰动振幅超过其饱和振幅,流体力学不稳定性进入非线性阶段.由于不同扰动模式之间的空泡和尖钉的耦合,需要同时考虑单模式饱和振幅和多模式饱和振幅[30]:

饱和振幅取这2 个数值中较小的那一个.当扰动进入弱非线性区后扰动增长率计算公式为[31]

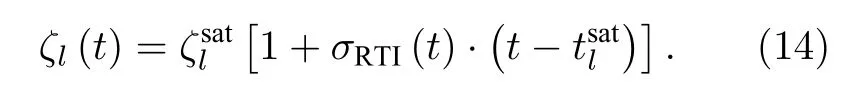
外表面扰动增长从冲击波突破后表面时刻开始,持续到 4.35 ns 外表面开始减速为止,减速的原因是锥的收缩导致壳层材料堆积使得外表面飞行速度减慢.内表面则因为壳层内部的压力以及本身是一个自由面,所以其速度一直在增加,不需要考虑RTI 增长而只受外表面增长的馈入影响.把(11)—(14)式代入第2 节中的解析模型进行计算,得到外表面最终扰动振幅随扰动模式l的谱分布如图7 所示.

图7 壳层外表面最终扰动振幅Fig.7.Final perturbation amplitudes of the outside surface of the shell.

图7 中模式数l=140—760 之间的初始扰动最后都进入了非线性增长区域,最危险的模式为l≈150—300,扰动增长率约 700—800,l＞1000 的短波长扰动模式基本都被表面烧蚀致稳作用抹平了.假设不同模式数的表面扰动相位完全随机,则扰动总振幅可以用均方根振幅表示:

为了保证壳层的完整性,壳层外表面扰动要满足

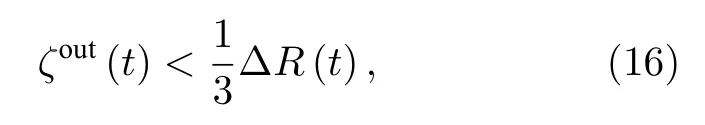
式中,ΔR(t)代表t时刻壳层厚度.从RTI 增长开始到外表面出现减速为止,壳层厚度和外表面总扰动振幅之间的关系如图8 所示.图中壳层厚度由MULTI 1D 模拟结果计算得到,在 2.9 ns 冲击波停止产生后 160 ps 壳层达到最薄,约 6.6 μm,扰动振幅为 0.72 μm.解析模型中壳层在 2.9 ns 时最薄只有约 2.6 μm,扰动振幅为 0.37 μm,依然处于安全范围.图8 中最危险时刻在约 4ns 时刻,此时扰动振幅和壳层厚度比达到 0.25,壳层比较安全.对于理论模型,最危险时刻同样出现在 4ns,扰动和厚度比为 0.2,考虑到理论模型中对壳层稀疏的简化处理,完整的理论模型中最危险时刻会出现得更早,且比值更大.

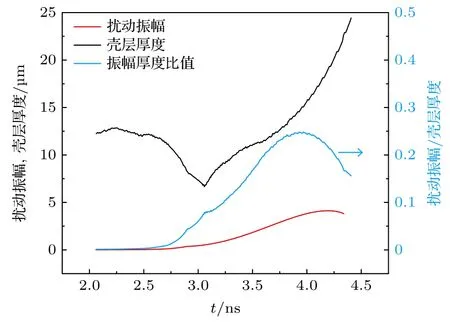
图8 不同时刻壳层厚度和外表面扰动振幅的演化Fig.8.Evolution of the thickness of the shell and perturbation amplitudes of the outside surface in different times.

壳层外表面的RTI 增长还会带来内表面的馈入机制,即由于壳层厚度有限,内表面会受外表面扰动影响产生增长,表示成[18]

假设内表面初始扰动和外表面一致,外表面增长带来的馈入扰动在RTI 增长结束时为 28.4 nm,初始扰动振幅约为 14.6 nm,最终内表面总扰动振幅约为 32 nm .壳层内表面一直加速,所以直到从锥口喷出都不会经历减速阶段的RTI 增长,但内表面扰动可能会影响出口等离子体的均匀性和对撞过程,增加飞行过程中的壳层厚度可以减弱馈入机制带来的内表面扰动增长.

4 壳层飞行和RTI 增长分析

在 2.1 ns 左右冲击波突破后表面之前理论和模拟对壳层密度和轨迹的描述非常吻合,随后壳层加速过程和冲击波产生过程同时进行直到 2.9 ns 光强达到峰值,此时理论模型计算得到燃料等熵参数αif≈2.1,密度ρ=17.6 g/cm3,壳层厚度 2.6 μm,模拟结果中ρ=8.7 g/cm3,ΔR=8 μm .这段时间的冲击波叠加受到自由面稀疏波影响,会出现明显的密度分布,所以模拟结果中峰值密度相比理论模型更低,壳层厚度明显更大.这些结果说明了当前设计下的激光波形对靶丸实现了近等熵高密度压缩.

随后的加速过程中,密度由等熵参数决定,烧蚀压不足以维持冲击波阶段产生的密度,壳层将会开始绝热膨胀.加速后期,燃料接近锥口不断堆积导致密度重新上升,厚度进一步增加,外表面出现减速,但内表面继续加速.整个加速过程模拟和理论模型对壳层轨迹的描述基本一致,包括不同时刻内外表面的位置和速度,壳层内表面物质将会在激光结束后 1ns 左右和对向锥口喷出的物质前锋相撞.

激光不均匀性和烧蚀RMI 不稳定性增长包含在RTI 增长的初始条件设置中,RTI 随壳层外表面的加速开始增长,初始扰动均方根振幅约为14.6 nm,外表面加速结束时扰动均方根振幅达到约 3.8 μm.l=140—760 之间的扰动模式进入了非线性增长区域,最危险的模式出现在l≈150—300,增长率在 750 左右.由于外表面后期的减速,RTI增长的总时间被缩短,内表面则因为一直加速所以不会出现RTI 增长,仅受到较弱的馈入影响.壳层在 2.9 ns 附近被冲击波压缩到很薄的厚度,ΔR＜8 μm,冲击波结束后壳层膨胀变厚,加上后期锥收缩进一步使燃料厚度增加,都增加了壳层抵抗不稳定性扰动增长的能力.在 4ns 左右不稳定性增长进入了一个相对危险的区域,此时外表面扰动均方根约为 3.74 μm,壳层厚度为 15 μm 左右,比值达到0.25,壳层依然处于安全范围.如果假设冲击波结束时刻扰动均方根振幅为 22 nm,则最危险时刻依然在 4ns 附近,扰动振幅和壳层厚度比值将达到约0.35,壳层存在很大的破裂风险.考虑到激光不均匀性和烧蚀RMI 的增长,当前方案下要求靶丸的初始表面扰动均方根振幅至少低于 20 nm .

对当前方案下RTI 增长贡献较大的因素包括,低熵压缩使得烧蚀速度较低,一部分高模式短波长扰动未能得到有效抑制,冲击波结束时壳层厚度较小,导致危险区域出现.壳层外表面密度梯度也偏小,Lmin在 0.2—0.7 μm 之间变化,小于通常点火方案中 1μm 左右的值[11,12].可以通过提高预脉冲强度,壳层中掺杂高Z材料等方式[32]提高烧蚀面密度标长,减小烧蚀RTI 增长率.

当前的分析中以流体力学过程为主,没有考虑激光-等离子体不稳定性(LPI)产生的影响.实际的点火过程中,LPI 会降低能量的吸收效率从而降低壳层加速度,产生额外的不均匀性导致长波长扰动增加,产生超热电子对靶丸加热导致熵增加密度降低[33,34].冬季实验中近等熵波形下靶丸对激光能量的吸收率在85%—90%之间,对LPI 抑制较好.未来激光能量提高可能导致LPI 效应增强,需要进一步考虑LPI 过程对计算RTI 增长所带来的影响.

5 结论

本文在双锥对撞点火方案的基础上,考虑了燃料壳层收缩和烧蚀面投影的影响,结合对壳层稀疏过程的简化处理以及烧蚀RTI 增长的解析公式,建立了一套分析压缩过程和RTI 增长的理论模型.理论和一维流体模拟结果对比显示出对不同时刻半径和加速过程描述的一致性,证明了方案对燃料低熵压缩的实现效果,由此得到外表面RTI 增长的完整过程.双锥对撞点火方案的加速后期呈现出壳层厚度增加,外表面减速等特点,这些特点有助于增加点火方案对流体力学不稳定性增长的抵抗能力.但是由于低熵压缩下的低烧蚀速度和很薄的壳层厚度,依然有一部分短波长扰动模式进入了非线性增长区域,在 4 ns 左右是最危险的时刻,此时扰动振幅和壳层厚度比达到约0.25,不过此时壳层依然安全,但留下的安全余量空间已经较小.当前设计下对初始时刻靶丸表面均匀性要求较高,可能需要进一步改善驱动激光焦面的匀滑度和靶表面的光滑度和构型.改进方案包括增加预脉冲,往壳层中掺杂高Z材料层,提高初始时刻壳层厚度等方法.对本文工作的进一步改进包括理论模型中壳层稀疏过程的更准确描述,引入实际测量的靶丸初始表面扰动振幅谱分布以及完整的烧蚀RMI 增长分析,同时还需要针对LPI 的影响进行更深入的讨论.