介孔尺度及结构对混合硝酸盐热输运特性的影响*
2022-02-17何卓亚杨启容李昭莹毛蕊王力伟闫晨宣
何卓亚 杨启容 李昭莹 毛蕊 王力伟 闫晨宣
(青岛大学机电工程学院,青岛 266071)
采用分子动力学方法模拟介孔尺度和结构对混合硝酸盐热输运特性的影响.使用Material Studio 软件分别建立不同尺度、两种结构的混合硝酸盐模型以及达到共晶状态的不同比例的NaNO3-KNO3 模型,通过对模型进行运算并整理计算结果,对纳米尺度下混合硝酸盐热输运特性的微观机理进行分析.结果表明:太阳盐的相变温度随着纳米孔尺度的增大呈现先增加后减小的趋势,最终与宏观尺度下的熔点一致;阳离子的比例对混合硝酸盐的相变温度有很大的影响,且纳米线结构也会改变硝酸盐的相变温度.硝酸盐的体热膨胀系数随着介孔尺度的增大而减小,随着NaNO3 含量的增加而增大,随着介孔结构的改变而改变.离子之间的相互作用的增强会使导热率增大,但对定压比热容没有太大影响.
1 引言
在众多相变材料中,硝酸盐因热稳定性良好且成本较低在集中式太阳能发电(CSP)系统[1]中得到了广泛的应用.在硝酸钠-硝酸钾二元盐中,最佳共晶状态混合物为50%硝酸钠-50%硝酸钾(质量分数,下文同),因成本较高,所以首选60%硝酸钠和40%硝酸钾的混合物.太阳盐(60%硝酸钠-40%硝酸钾)的熔点约为493 K,潜热在110.01 kJ/kg左右[2],但是硝酸盐存在着过冷、液相泄漏、导热率低等一系列问题.为了解决这些问题,科研工作者们采用添加纳米颗粒[3,4]、微胶囊封装[5]、多孔骨架材料吸附[6-8]等方法制备复合相变储能材料.近几年来,多孔复合相变储能材料的研究主要集中在多孔骨架材料的精选和优化上,多孔材料呈现出孔径尺寸越来越小[9]、孔道结构越来越有序、比表面积越来越大的趋势[10-12].Gibbs-Thomson 方程指出:
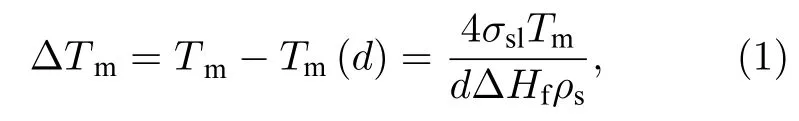
式中,ΔTm为熔点,σsl为表面张力,Tm为初始相变温度,ΔHf为相变焓,ρs为固态密度,d为孔径.
(1)式表明熔点与孔径d的倒数呈线性关系.因此,研究相变材料在不同孔径和孔结构中的热输运特性对于相变储能效率的提高和相变封装技术的发展具有非常重要的意义.
Bore 等[13]研究了多孔骨架介孔二氧化硅的孔径和孔结构对金纳米粒子热烧结的影响,发现三维六角形和立方形孔结构的样品比二维六角形孔结构的样品更易发生烧结,且孔径的增大会促进复合相变材料的烧结情况.Zhang 等[14]和Wang 等[15]研究了介孔二氧化硅对有机相变材料相变行为的影响,研究表明随着介孔二氧化硅MCM-41 孔径的减小,复合相变材料的熔点、潜热和比热容逐渐增大.具有特殊结构的多孔骨架通过改变对相变材料的表面张力、毛细管力[6,16]等物理作用力,促进了对相变材料的吸附,因此热物理性能和储能密度大幅度提升[17].Min 等[18]和Gao 等[19]分别制备了发射状孔道和纳米花状皱纹状孔道的聚乙二醇/介孔二氧化硅复合相变材料,这两种介孔结构有效提高了聚乙二醇的吸附量以及复合相变材料的熔化焓和凝固焓.综上,由于孔材料的特殊介孔结构,小尺寸(纳米限域下)物质会表现出与宏观尺度不同的热力学现象,因此多孔骨架基体的孔径和孔结构对相变材料的相变特性存在一定的影响.
介孔内填充物的典型纳米材料,如零维的纳米颗粒、一维的纳米线及三维的纳米颗粒团聚体,是由原子、分子过渡到宏观块材的一类新的微观存在.块材物质的物理性质通常与大小无关,但是在纳米尺寸上并非如此.小尺度效应及特殊结构使纳米材料的热物理性质相对于体材料表现出特异性,而这些特异性将显著影响介孔纳米材料的相变热输运行为,从而影响复合相变材料的性能.近几年的研究大多集中在纳米金属粒子[20,21]和有机相变材料[22]的微尺度效应,如熔点尺度效应、比热增加及导热率低准效应等[23],对硝酸盐/多孔陶瓷复合相变材料热物性的测量多在宏观尺度下进行[24,25],测量纳米尺度下孔内相变材料的相变特性较难,从而模拟纳米尺度下介孔内硝酸盐的热输运特性可为复合相变材料相变性能参数的调控提供理论依据.
本文采用分子动力学的方法[16],探究介孔的尺度和结构对混合硝酸盐热输运特性的影响.借鉴纳米金属粒子和有机聚合物模型[11]的模拟过程,使用Material Studio 软件建立离子数不同和结构不同的太阳盐模型以及达到共晶状态[26]的不同比例的NaNO3-KNO3模型,通过模拟数据的整理分析,总结径向分布函数、相互作用能、相变温度、体热膨胀系数、导热率和定压比热容等参数的变化,对纳米尺度下混合硝酸盐相变特性的微观机理进行分析.
2 模拟
2.1 模型建立
混合硝酸盐的模型为硝酸钠(NaNO3)和硝酸钾(KNO3),两种材料在结晶学开放数据库(Crystallography Open Database)进行下载并重新计算化学键和其键能,去对称后进行径向分布函数等计算,结构如图1.在Material Studio 软件中去对称后运用Amorphous Cell 模块的Calculation 来建立模型,加入NaNO3和KNO3构建混合硝酸盐模型.通过增减NaNO3和KNO3的数量建立不同比例的二元混合硝酸盐模型、不同尺度的太阳盐(数量比w(NaNO3)∶w(KNO3)=6∶4)模型和不同结构的太阳盐模型,将自由状态下模拟盒子内的混合硝酸盐模型设定为纳米孔内的硝酸盐模型,而晶胞拉伸为长方形的混合硝酸盐模型设定为纳米线硝酸盐模型.不同比例的硝酸盐模型的离子总数保持在460 个离子左右,不同尺度的太阳盐模型的离子总数为460,920,1380,1840,2300,2760,两种孔结构的太阳盐模型的离子总数为460 和920,各类混合硝酸盐中NaNO3和KNO3的具体数量以及模型的尺度如表1 和表2 所列,结构如图2 所示.
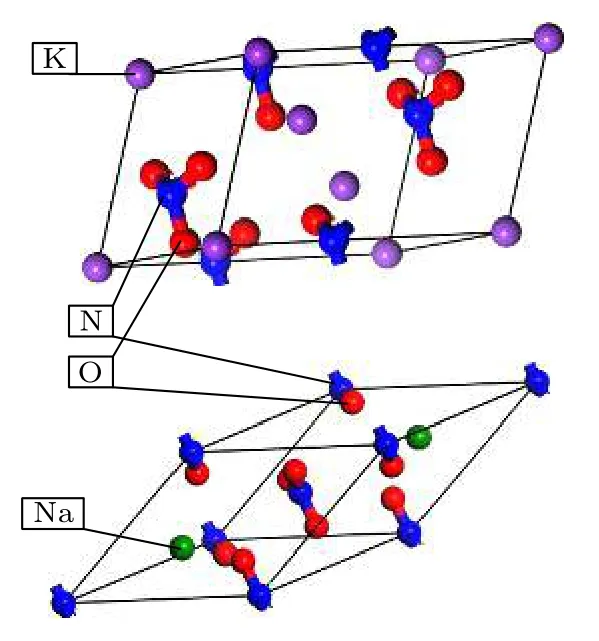
图1 NaNO3 和KNO3 的单晶胞Fig.1.NaNO3 and KNO3 single crystal cells.

图2 混合硝酸盐模型 (a)w (NaNO3)∶w (KNO3)=4∶6混合硝酸盐;(b)w (NaNO3)∶w (KNO3)=5∶5 混合硝酸盐;(c)w(NaNO3)∶w(KNO3)=9∶1 混合硝酸盐;(d)w(NaNO3)∶w(KNO3)=6∶4 太阳盐;(e)w(NaNO3)∶w(KNO3)=6∶4 异结构太阳盐Fig.2.Mixed nitrate model:(a)w(NaNO3)∶w(KNO3)=4∶6 mixed nitrate;(b)w(NaNO3)∶w(KNO3)=5∶5 mixed nitrate;(c)w(NaNO3)∶w(KNO3)=9∶1 mixed nitrate;(d)w(NaNO3)∶w(KNO3)=6∶4 solar salt;(e)w(NaNO3)∶w(KNO3)=6∶4 heterogeneous solar salts.
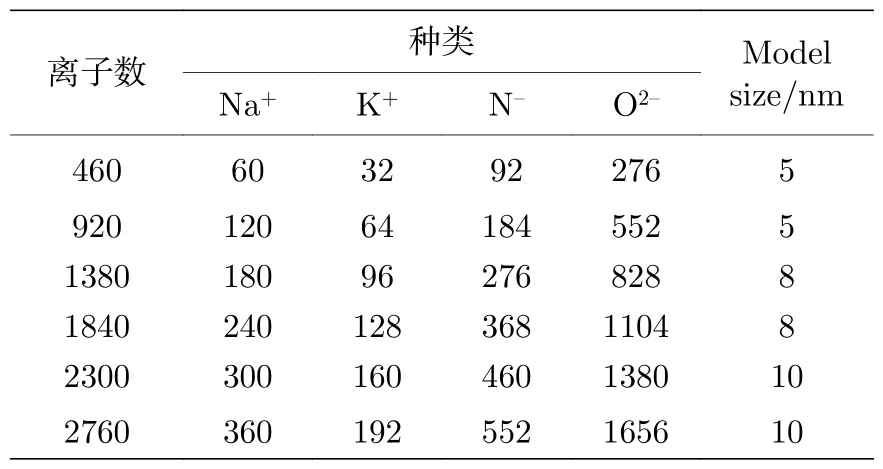
表1 太阳盐(w(NaNO3):w(KNO3)=6:4)中NaNO3和KNO3 的离子数Table 1. Ion numbers of NaNO3 and KNO3 in solar salts (w(NaNO3):w(KNO3)=6:4).

表2 混合硝酸盐中NaNO3 和KNO3 的离子数(总离子数为460)Table 2. Ion numbers of NaNO3 and KNO3 in mixed nitrate (total number of ions is 460).
2.2 模拟方法
二元混合硝酸盐的模拟采用的力场为通用力场(universal force field,UFF).在通用力场中,范德瓦耳斯力是由Lennard-Jones (L-J)势能[27]来表示,其公式为
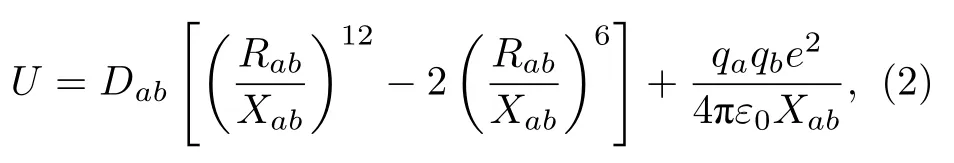
式中,Xab是不同分子a和b中的原子间的距离,单位为Å;D和R分别是分子中不同原子间的L-J势能的能量参数和尺度参数,单位分别为kcal/mol和Å;q是分子中各原子所带的部分电荷;ε0是自由介电常数;e是电荷的单位;下标a,b分别代表不同分子中的原子对.
混合硝酸盐模型首先采用Forcite 模块的Geometry Optimization 进行几何优化,算法为Smart,计算力场为UFF,然后继续使用该模块当中的Dynamic 任务,对范德瓦耳斯力采用截断半径法,截断半径小于立方晶格边长的一半,长程静电相互作用力修正则采用Ewald 加和法计算.在模拟中由于计算时间较短,所以需要高压来提供混合硝酸盐所需的能量[28],压力设定为0.1 GPa,由Berendsen方法控制;温度分别设定为323,373,423,473,523,573,623,673,723,773 K,由Nose 方法控制.在等温等压系综(NPT)下,静电相互作用力和范德瓦耳斯力分别选用PPPM 和Ewald[29],时间步长为1 fs 运行100 ps,使体系达到平衡.在正则系综(NVT)条件下,静电相互作用力和范德瓦耳斯力仍选用PPPM 和Ewald[29],继续运算70 ps 达到平衡,并使用该模块下的Analysis 分析径向分布函数(radial distribution function,RDF)和均方位移(mean squared displacement,MSD)等数据.
混合硝酸盐的微观结构和原子之间的相互作用能用RDF 来表征,RDF 用来描述参照粒子周围其他粒子分布的物理量,其公式为

式中:ρβ为β粒子的数量密度;Nαβ(r)表示位于以α粒子为中心、r为半径的球体内β粒子的平均数.
混合硝酸盐中NaNO3和KNO3之间的相互作用能的绝对值越大,表明两者之间的相互作用越强,体系内热量传递效果越好.相互作用能Einteraction(kcal/mol)[30]的计算式为

式中,ETotal为混合硝酸盐的总能量,为NaNO3的总能量,为KNO3的总能量,单位均为kcal/mol.
在分子动力学模拟中,体系粒子由起始位置不停地发生位移,每一瞬间各粒子的位置皆不相同,粒子位移平方的平均值即为MSD,单位为Å2,其公式为

式中,M为均方根位移值MSD,ri(t)和ri(0)分别代表第i个粒子在t和0时刻的坐标.
自扩散系数D是随着温度T变化而变化的函数,该系数的值可以用来表示系统是否有相变发生.自扩散系数D(m2/s)的计算采用爱因斯坦方程,其公式为

式中,m表示体系的维度,N代表体系中的目标分子数,[ri(t)-ri(0)]2为MSD.对MSD 曲线进行数据拟合,直线斜率α即为:,因为MSD 已经对体系中粒子数进行了平均,所以自扩散系数D可简化为D=α/6.
采用Müller-Plath[31]提出的反向非平衡分子动力学方法,通过交换原子的速度矢量来构造热流,并将能量通量jZ(W·m—2)应用于模型的z方向,同时保证计算过程总动量、总动能和总能量的守恒.当达到稳态时,可以获得混合硝酸盐z方向的温度梯度,混合硝酸盐的导热系数λ(W·m—1·K—1)可以通过能量通量jZ和混合硝酸盐z方向上温度梯度dT/dz进行计算,计算公式为

能量通量jZ(W·m—2)的计算公式为

式中,t表示能量交换时间;A表示能量通量方向的截面积,单位为m2;m表示参与能量交换的原子总质量,单位为u;vh和vc分别表示混合硝酸盐内热域原子和冷域原子的速度,单位为m/s.
3 结果与分析
3.1 径向分布函数和相互作用能
RDF 通常用来研究系统的有序性,该函数能从整体、全局的角度反映出系统中粒子的聚集特性[32].模拟不同温度条件下太阳盐体系中w(K+)-w(Na+),w(K+)-w(N—),w(Na+)-w(N—)的RDF,以w(K+)-w(N—),w(Na+)-w(N—)的RDF 代表w(K+)-w(NO3—),w(Na+)-w(NO3—)的RDF,具体的结果如图3 所示.

图3 不同温度下离子之间的径向分布函数 (a)w(K+)-w(Na+);(b)w(K+)-w(N—);(c)w(Na+)-w(N—)Fig.3.Radial distribution function of ions at different temperatures:(a)w(K+)-w(Na+);(b)w(K+)-w(N—);(c)w(Na+)-w(N—).
w(Na+)-w(N—)和w(K+)-w(N—)RDF 图与Anagnostopoulos 等[32]所模拟的RDF 图基于相一致.随着距离增加,峰变得平缓,逐渐趋近于1,这说明太阳盐液态短程有序、长程无序的特点.w(K+)-w(N—)和w(Na+)-w(N—)的第二个峰变得较弱,揭示了阴阳离子的不规则生长.随着温度的增高,w(K+)-w(Na+),w(K+)-w(N—),w(Na+)-w(N—)的第一峰峰值减小,峰谷变高,w(K+)-w(Na+)峰值右移,温度的增高使得分子运动的随机性变强,阳离子-阳离子结构变得有所松散;但由w(K+)-w(N—),w(Na+)-w(N—)峰值的位置没有变化,可以看出温度对阳离子-阴离子之间的距离没有什么影响.温度较低时w(K+)-w(Na+)第二峰峰值较高,说明较低温度时K+-Na+离子之间有着较好的相互作用,结构排列有序,而较高温度下w(K+)-w(Na+)第二峰峰值下降,w(K+)-w(Na+)离子排列逐渐无序,相互作用减弱.
图4 为不同尺度下太阳盐阳离子-阳离子和阳离子-阴离子的径向分布函数和相互作用能.随离子数的增加,n(K+)-n(Na+),n(K+)-n(N—),n(Na+)-n(N—)的第一峰峰值增高,谷深增大,说明离子团簇内n(K+)-n(N—)和n(Na+)-n(N—)之间的相互作用增强,阳离子-阴离子的排列更有序.n(K+)-n(Na+),n(K+)-n(N—),n(Na+)-n(N—)第一峰峰值和谷深左移说明了阳离子-阳离子和阳离子-阴离子之间的距离被拉近,离子结构变得更加有序紧凑.随着离子数的增加,NaNO3和KNO3之间的相互作用能得到显著加强,在473 K 时由10 kcal/mol 增加到68 kcal/mol,说明混合硝酸盐之间的相互作用位点增多,这有利于太阳盐体系内部热量的传递,对导热性能等热物性产生有利的影响.

图4 不同尺度下离子之间的径向分布函数和相互作用能 (a)n(K+)-n(Na+);(b)n(K+)-n(N—);(c)n(Na+)-n(N—);(d)相互作用能Fig.4.Radial distribution function and interaction energy of ions at different scales:(a)n(K+)-n(Na+);(b)n(K+)-n(N—);(c)n(Na+)-n(N—);(d)interaction energy.
图5 为不同比例下二元混合硝酸盐的径向分布函数和相互作用能.除质量比w(Na+):w(K+)=5∶5 外,随着NaNO3含量的增加,w(K+)-w(Na+),w(K+)-w(N—),w(Na+)-w(N—)的峰值减小,谷深减小,峰的宽度右移,这表明NaNO3含量的增加使得离子团簇内阳离子-阴离子之间的距离变大,相互作用减弱,也影响了NaNO3和KNO3之间结合,相互作用能降低.w(Na+):w(K+)=5∶5 比例的径向分布函数突变说明该比例的混合硝酸盐可以得到更好的共晶状态.

图5 不同比例下离子之间的径向分布函数和相互作用能(w(NaNO3):w(KNO3))(a)w(K+)-w(Na+);(b)w(K+)-w(N—);(c)w(Na+)-w(N—);(d)相互作用能Fig.5.Radial distribution function and interaction energy of ions at different proportions (w(NaNO3):w(KNO3)):(a)w(K+)-w(Na+);(b)w(K+)-w(N—);(c)w(Na+)-w(N—);(d)interaction energy.
由图6 可见,纳米线太阳盐的n(K+)-n(Na+)和n(K+)-n(N—)的RDF 图的第一峰的峰值均大于相同离子数的纳米孔内太阳盐的第一峰的峰值,Na+-N—的RDF 图的第一峰峰值小于相同离子数纳米孔结构内太阳盐的第一峰的峰值,而出现峰值的距离没有变化,说明离子团簇之间的距离没有发生变化,改变孔结构后n(K+)-n(Na+)和n(K+)-n(N—)之间有着很好的作用力.就相互作用能而言,太阳盐纳米线的相互作用能高于纳米孔内太阳盐的相互作用能,这表明结构的改变会影响NaNO3和KNO3之间的相互作用位点,从而提高混合硝酸盐的导热性能.
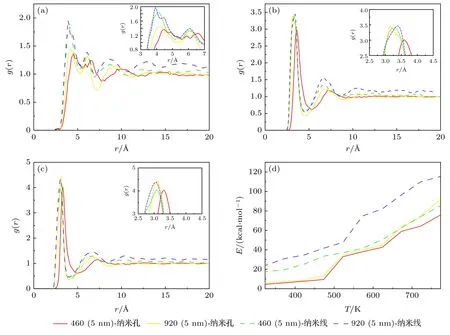
图6 两种结构下离子之间的径向分布函数和相互作用能 (a)n(K+)-n(Na+);(b)n(K+)-n(N—);(c)n(Na+)-n(N—);(d)相互作用能Fig.6.Radial distribution function and interaction energy of ions at two structures:(a)n(K+)-n(Na+);(b)n(K+)-n(N—);(c)n(Na+)-n(N—);(d)interaction energy.
3.2 相变温度
二元硝酸盐体系内扩散越快,表明体系内离子的流动性越强,所以当自扩散系数的数值有明显的变化时,说明在该温度下发生了相变.
图7 是纳米孔内离子数为2760 的太阳盐的均方位移和自扩散系数,以此为例,不同尺度下的太阳盐的相变温度模拟结果如表3 所列.宏观尺度下太阳盐熔点的结果为493 K[34],当太阳盐的模型离子数达到2760 后,模拟结果与其误差为0.2%,离子数达到5520 时模拟结果与宏观尺度太阳盐熔点的结果一致.由表3 可见,随着离子数的增大,熔点呈先增大后减小的趋势,体现了纳米尺度下硝酸盐热特性的尺度效应.

表3 不同尺度下太阳盐的相变温度Table 3. Phase transition temperature of solar salts at different scales.

图7 离子数为2760 的太阳盐的均方位移和自扩散系数 (a)均方位移;(b)自扩散系数Fig.7.Mean square displacement and self diffusion coefficient of solar salt with ion number of 2760:(a)Mean square displacement;(b)self diffusion coefficient.

式中,Tm(D)为纳米晶体的熔化温度,D为有效直径,Tm(∞)为大块的熔化温度,Vs为大块晶体的摩尔体积,γsl为固-液相的界面能,Hm(T)为摩尔熔化焓,δ为表面处熔化液层的厚度.
由(9)式可知,当纳米晶体直径D<10 nm或者其表面体积比hA/V>10%(h,A,V分别为原子直径、表面积、体积)时,δ的大小是与尺寸D相当的量,则表面熔化变成一个不可忽视的因素[35-37].太阳盐的比表面积(表面积/质量)与直径成反比,在一定尺度范围内,随着离子数的减小,比表面积会显著增加,表面离子在太阳盐总离子数中占据的比例越大,表面能的比重也变大,这样表面的离子活性更大,极易与其他离子结合以寻求更稳定的结构,原结构不稳定,要打破原结构所付出的能量越低;且离子数较小时,阳离子-阴离子之间的相互作用较弱,相互作用能较小,发生相变时所需要的能量较小.当离子数增多时,熔化方式逐渐发生改变,由表面熔化逐渐转变成体熔化[38],熔点进一步升高;但是当离子数进一步增多,即D>10 nm 时,熔化机理与D<10 nm 的熔化机理不尽相同[39],表面熔化与体熔化同时发生,且由(10)式可知,当D→∞时,表面能的占比减小,尺度效应逐渐消失,相变温度逐渐接近宏观尺度下的相变温度,Tm(D)→Tm(∞)[40].由此可知,骨架的孔径大小存在一个最佳值.
表4 为不同比例的混合硝酸盐的相变温度模拟结果,文献[34]中宏观尺度下混合硝酸盐熔点分别为496 K (w(K+)-w(Na+)=4∶6),491 K (w(K+)-w(Na+)=5∶5),558 K (w(K+)-w(Na+)=9∶1),模拟结果与文献的误差都在5%以内.Na+和K+的比例改变,离子之间的作用力强度发生变化,从而影响了共晶状态.其中w(K+)-w(Na+)=5∶5 比例的混合硝酸盐的相互作用较其他比例的混合硝酸盐来说较强,其共晶状态最佳,熔点较低,这表明离子之间的相互作用影响了二元混合硝酸盐的共晶状态,从而影响了熔点.
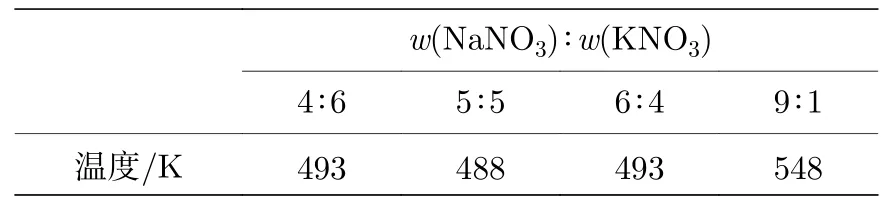
表4 不同比例的混合硝酸盐的相变温度Table 4. Phase transition temperature of mixed nitrates at different proportions.
表5 显示了纳米线结构太阳盐的相变温度模拟结果.与纳米孔内的太阳盐相比,该种孔内的太阳盐的相变温度更高.改变孔结构后,太阳盐体系中离子之间的作用力较强,相互作用能较高,导致离子活性较小,原结构较稳定,要打破原结构所付出的能量较高.

表5 纳米线结构太阳盐的相变温度Table 5. Phase transition temperature of nanostructured solar salts.
3.3 体热膨胀系数
体热膨胀系数α(K—1)是指压力一定的情况下,体积随温度变化的变化率.体热膨胀系数越小,说明当温度变化时体积变化越小.

根据体热膨胀系数的(11)式可知,与体热膨胀系数大小相关的2 个参数是体积V和压力一定时体积随温度变化的变化率.
图8 为不同尺度下随温度变化太阳盐的体热膨胀系数和体积变化图.由图8 可知,太阳盐的体热膨胀系数随着温度的升高逐渐减小,且随着离子数的增加最大体热膨胀系数减小.这与太阳盐内部离子结构和相互作用能的变化有关.

图8 不同尺度下太阳盐的体热膨胀系数和体积 (a)体热膨胀系数;(b)体积Fig.8.Thermal expansion coefficient and volume of solar salts at different scales:(a)Thermal expansion coefficient;(b)volume.
温元凯和李振民[41]根据Winkler 对热膨胀系数的机理的分析,认为线热膨胀系数与结合能成反比关系,得出:
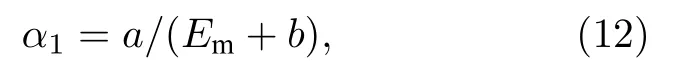
式中,α1为线热膨胀系数,单位为K—1;a,b为常数,取决于晶格类型;Em表示结合能,单位为kcal/mol.
随着温度的升高,阳离子-阳离子、阳离子-阴离子之间的距离变大,离子之间的作用力减弱,从而太阳盐体积增大,密度降低,由(11)式和(12)式可知,当定压下体积随温度的变化一定时,V越大,体热膨胀系数α越小;相互作用能越强,体热膨胀系数α越小.
随着离子数的增大,阳离子-阳离子、阳离子-阴离子的距离拉近,离子作用力增强,定压下体积随温度的变化减小,但由于体积V的变化大于定压下体积随温度的变化,且太阳盐的相互作用能随离子数的增大而增大,所以热膨胀系数α变小.
如图9 所示,随着NaNO3含量的增高,NaNO3-KNO3二元混合硝酸盐的体热膨胀系数呈现逐渐增高的趋势.在相同温度下,由于NaNO3含量的增高,阳离子-阳离子、阳离子-阴离子之间的距离变远,定压下体积随温度的变化变大,体积V逐渐减小,又因相互作用能逐渐降低,热膨胀系数α变大.

图9 不同比例下太阳盐的体热膨胀系数和体积(w(Na+)∶w(K+))(a)体热膨胀系数;(b)体积Fig.9.Thermal expansion coefficient and volume of solar salts at different proportions (w(Na+)∶w(K+)):(a)Thermal expansion coefficient;(b)volume.
图10 给出了两种结构太阳盐的体热膨胀系数和体积随温度的变化规律.与相同离子数的纳米孔内的太阳盐的体热膨胀系数和体积相比,纳米线太阳盐的体热膨胀系数小于纳米孔内太阳盐的体热膨胀系数.纳米孔内太阳盐离子之间的作用力和相互作用能均小于纳米线太阳盐离子之间的作用力和相互作用能,在定压下体积随温度的变化大,而相同离子数时两者体积V基本一致,所以纳米线太阳盐的体热膨胀系数小于纳米孔内太阳盐的体热膨胀系数.

图10 两种结构下太阳盐的体热膨胀系数和体积 (a)体热膨胀系数;(b)体积Fig.10.Thermal expansion coefficient and volume of solar salts at two structures:(a)Thermal expansion coefficient;(b)volume.
以上不同尺度、不同比例、两种结构的混合硝酸盐的体热膨胀系数与Lonappan[42]的纯KNO3数值2.28×10—4K—1的数量级一致.
3.4 导热率
当一种颗粒的空间尺寸达到纳米颗粒的尺寸级别时,因随着尺寸的变化,热物性是呈指数形式变化的,所以在讨论热物性尤其是导热率变化时,不能忽略小尺寸效应带来的影响.以张景胤[43]根据玻尔兹曼热传导方程的弛豫时间近似建立的概率效应为基础,具体公式为

式中,kp和分别表示纳米颗粒和块体的导热率;X为无量纲量,X=r/Λ,其中r表示纳米粒径,Λ表示声子的自由程.越小的纳米粒子粒径,会造成越强的声子散射,就会带来更低的导热率.
图11 为不同尺度下太阳盐导热率的变化曲线,且460 离子数各个混合硝酸盐模型的导热率模拟值与Kenisarin 等[44]的实验结果的误差在10%左右.随着离子数的增大,导热率也在逐渐增大,离子数从460 增大到2760,导热率从0.46 W·m—1·K—1增大到0.76 W·m—1·K—1.离子之间距离减小,离子作用力加强,太阳盐体系内的相互作用能增大,提高了太阳盐体系内部热量的传递,且根据(13)式可知,离子数的增大使模型半径r增大,从而无量纲量X增大,声子的运动距离增加,声子的约束效应逐渐减弱,声子运动得更加剧烈,由此导热系数得到提升.当声子运动距离达到声子平均自由程时,导热率不再升高.

图11 不同尺度下太阳盐导热率Fig.11.Thermal conductivity of solar salts at different scales.
如图12 所示,随着NaNO3含量的增大,导热率逐渐减小,由于NaNO3含量的变化导致二元硝酸盐内Na+和K+的比例发生变化,从而导致离子之间的作用力及作用能发生变化.NaNO3含量越多,离子之间距离增大,相互作用减弱,导致相互作用能减小,从而降低混合硝酸盐体系内部的热量传递,且不同频率的声子之间的有效传递能量随之减弱,导热率越低.

图12 不同比例下混合硝酸盐导热率Fig.12.Thermal conductivity of mixed nitrates at different ratios.
表6 显示了离子数为460 和920 时两种结构的太阳盐的导热率.相比于长度较短的纳米孔内太阳盐的导热率,纳米线太阳盐的离子之间有着更好的相互作用,相互作用能大大提高,且随着纳米线长度的增加,声子的运动距离大大增加,声子运动加剧,沿着离子键传导方向的热量提高,使得导热性能大大增强.

表6 两种结构下太阳盐导热率Table 6. Thermal conductivity of solar salts at two structures.
3.5 定压比热容
采用能量波动法计算混合硝酸盐的定压比热容Cp(J·g—1·K—1),在等温等压系综(NPT)下进行的模拟计算,其公式为
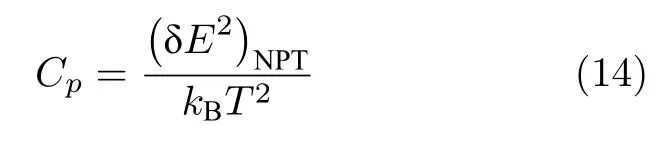
式中,E是总能量(动能和势能之和),单位为J;kB是Boltzmann 常数,单位为J/K;T是温度,单位为K.
(14)式可以简化为以下两个公式[45]:

式中,a,b,c,c′是经验常数,随物质的不同和温度变化范围的不同而不同.
从图13 和图14 可见,NaNO3的比热模拟值与653 K 液态经验值1.67 J·g—1·K—1的误差在1%左右,KNO3的比热模拟值与733 K 液态经验值1.39 J·g—1·K—1的误差在6%左右[46].随着离子数的增加,太阳盐的定压比热容没有较大的变化,代表着比热容与尺度没有较大的关系,且由(15)式和(16)式可看出,定压比热容主要与物质的种类和温度变化范围有关,这与导热率所呈现的规律不同.

图13 不同尺度下太阳盐定压比热容Fig.13.Fixed-pressure specific heat capacity of solar salts at different scales.
图14 显示了不同比例下二元混合硝酸盐的定压比热容随温度的变化曲线.从图14 可以看出,定压比热容并未随着NaNO3含量的增大而规律变化,太阳盐的比热值最大.由于NaNO3含量的变化导致二元硝酸盐内离子对比例发生变化,这与体系内部离子结构和相互作用变化引起的导热率的变化不同.

图14 不同比例(w(Na+)∶w(K+))下混合硝酸盐定压比热容Fig.14.Fixed-pressure specific heat capacity of mixed nitrate at different ratios (w(Na+)∶w(K+)).
综上可以看出,体系内部离子之间的结构变化和相互作用对定压比热容的大小影响不大,离子对比例的变化会影响定压比热容的变化.
4 结论
因实验中测量纳米孔径下的相变材料热物性较难,采用平衡分子动力学模拟和反向非平衡分子动力学模拟的方法,对不同尺度、不同比例和两种结构下的二元混合硝酸盐的热输运特性进行研究,结论如下:
1)太阳盐体系内部离子之间的作用力和相互作用能随着尺度的增大而增大,这有利于系统内部热量的传递;随着NaNO3含量的逐渐增加,二元混合硝酸盐离子之间的相互作用呈现逐渐减弱的趋势,但当w(NaNO3)∶w(KNO3)=5∶5 时,该比例下得到更好的共晶状态;改变太阳盐的结构后,太阳盐内部离子之间的作用力和相互作用能得到大幅度加强.
2)随着离子数的增大,太阳盐的相变温度呈现先增大后减小的趋势,说明骨架的孔径大小有一个最佳值;当NaNO3的含量逐渐增加,相变温度也随之改变,离子之间的相互作用影响了二元混合硝酸盐的共晶状态,从而影响了熔点;改变结构后,纳米线太阳盐的相变温度大于相同离子数时纳米孔内太阳盐的相变温度.
3)随着温度的升高,混合硝酸盐的体热膨胀系数逐渐减小;随着离子数的增大,太阳盐的体热膨胀系数逐渐减小;随着NaNO3含量的增加,二元混合硝酸盐的体热膨胀系数呈逐渐升高的趋势;与纳米孔内的太阳盐相比,相同离子数下纳米线太阳盐的体热膨胀系数更小.
4)随着离子数的增大,太阳盐的导热率越大;随着NaNO3的含量增加,二元混合硝酸盐的导热率逐渐减小;纳米线太阳盐的导热率大于相同离子数下纳米孔内太阳盐的导热率.而定压比热容并没有随着尺度的增大而有较大的变化,仅随体系内NaNO3和KNO3的比例变化而变化.
在本文已有研究的基础上,后续将研究骨架的表面对相变材料热输运特性的影响并开展相应的实验研究,综合得出介孔骨架—混合硝酸盐热输运特性的尺度效应、结构效应和界面效应,为提出介孔复合相变材料相变性能参数的调控方法提供理论依据.
