埋深对巷道围岩松动圈的影响研究

于占军，杨玉中，左 宝，刘 军

(1.河南理工大学 能源科学与工程学院，河南 焦作 454003；2.平顶山天安煤业股份有限公司 六矿，河南 平顶山 467000；3.河南理工大学 安全科学与工程学院，河南 焦作 454003)

地下巷道开挖后，扰动破坏了围岩原有的应力状态，导致围岩应力由三向应力状态重新分布到双向应力状态，随着应力的变化，巷道周围的岩体逐渐破碎，形成指向巷道的破碎带，称为围岩松动圈。由于深部开采具有高地应力、复杂应力的状态导致围岩松动圈的破坏范围在深部矿井尤为明显。巷道合理的支护参数是保证巷道稳定性，避免巷道发生大变形，塑性流动的有效措施。开展针对巷道的松动圈分布研究，对于支护参数的选取具有参考价值，故针对松动圈的分布研究，对于解决深部矿井巷道支护问题具有重要意义。

许多学者对围岩塑性区的分布进行了研究。马念杰等[1]针对深部采动巷道围岩应力环境，分析了双向非等压条件下巷道围岩塑性区形成的力学机制及其形态特征，并对顶板稳定性影响因素进行了探讨。Zhang Jia-hua等[2]基于非线性摩尔库伦准则，导出了浅埋双隧道稳定性能以及支护力的解析解，并分析了埋深、荷载、孔隙水压力、非线性系数对支护力的影响。曹平等[3]提出了拱梁与支护组合方案，改进了围岩压力拱的计算方法，建立了楼板梁的力学模型。徐坤等[4]将声波法应用到了现场实际中，准确得到了不同深度岩体的纵波波速，通过波速的变化测得松动圈的范围。康红普等[5]利用UDEC数值模拟软件，研究了深埋巷道的围岩和支护应力随着支护条件和围岩性质的改变的变化规律。郭晓菲等[6]利用FLAC3D软件结合现场实测对开采条件下塑性区和破坏区的分布和形态，以及采掘扰动对巷道变形的影响进行了研究，得到了巷道支护和煤柱的合理尺寸。孙晓明等[7]用数值模拟法研究了锚杆分别和围岩在强度、刚度、结构上耦合时对围岩强度、支护作用、应力场和位移的演化规律的影响作用。

本文以玉溪煤矿地质条件为工程背景，利用声波法测试了中央辅助运输大巷的松动圈范围，同时结合数值模拟研究了不同深度条件下的松动圈演化规律，研究结果对于玉溪煤矿巷道支护具有指导意义。

1 玉溪煤矿试验地点概况

玉溪煤矿属于沁水县胡底乡管辖，主采3号煤层厚度5.12～7.20 m，平均5.85 m，原始瓦斯含量为26.38 m3/t，瓦斯压力为1.65 MPa，埋深505～862 m，具有突出危险。矿井设计产能240万t/a。煤层顶板为泥岩、砂质泥岩、粉砂岩，局部为细粒砂岩，底板为泥岩，地层局部综合柱状图如图1所示。根据现场实际情况选择玉溪煤矿中央辅助运输大巷作为岩石巷道松动圈测试地点。中央辅助运输大巷布置在3号煤层底板下的岩层中，埋深660 m左右，围岩主要以砂质泥岩和粉砂岩、页岩为主，巷道断面为直墙半圆拱形断面，宽5.4 m，高4.3 m，断面积为20.1 m2。

图1 地层局部综合柱状图

2 岩石巷道松动圈现场测定

根据玉溪煤矿围岩巷道的实际情况，采用声波法测定岩石巷道松动圈的范围。仪器设备选用CT-2型围岩裂隙探测仪。测定地点选在玉溪煤矿中央辅助运输大巷的第四岩石巷道联络巷南部80 m、85 m、90 m位置进行测定。测试前选用75 mm钻杆，施工孔深为4 m，倾角为5°的下向钻孔，具体地点及钻孔布置如图2所示。

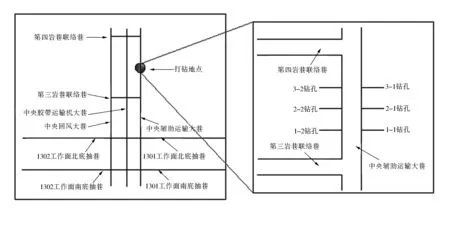
图2 中央辅助运输大巷钻孔示意

声波法测定松动圈测定步骤如下：

1) 在前期定下的现场实验地点，垂直于巷帮位置进行施钻，钻孔深度为5 m，当钻孔形成后，对钻孔扫眼，清出孔中岩粉和碎石碴，利用清水对钻孔进行清洗，直到钻孔内排出水未含岩渣为止。

2) 在仪器中安装电池后，先检查仪器显示及电路是否正常，然后螺旋连接测杆和收发装置，通过测杆将接收探头、发射探头送入钻孔底部位置(需要两人配合)，其余的附属装置放在孔口适当位置，利用堵水塞进行密封，通过注水口进入耦合剂(水)，直到金属杆端部连续出水。

3) 打开仪器进行测量后，拉动刻有刻度的铜金属测量杆向外移动，即可测出孔内不同深度的围岩波速，每个位置记录4组数据，且在测量结束后，向外拉动0.1 m，直至试验结束。

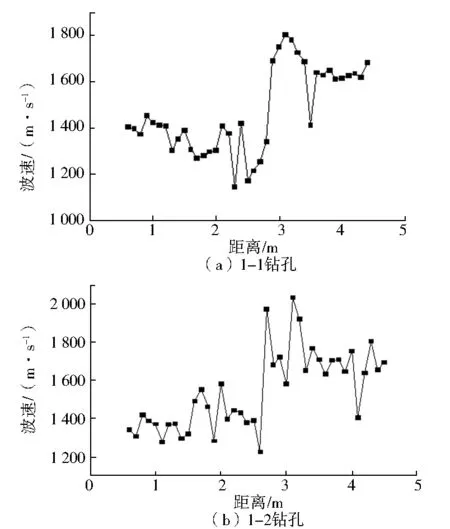
4) 整理数据，对每个位置测量得到的4组数据求平均数。将波速作为纵坐标，距巷帮的距离作为横坐标，绘制波速与距巷帮距离的关系图。根据现场测定，可以得出玉溪煤矿中央辅助运输大巷松动圈的范围，如图3所示。

从图3可以看出，中央辅助运输大巷1-1号钻孔在距离巷帮2.9 m范围内，超声波波速在1 145～1 457 m/s之间波动，平均1 335 m/s；距离巷帮2.9～3.4 m范围内，超声波传播速度明显增大，在1 685～1 800 m/s之间，平均1 739 m/s，增长了30%，说明在此范围内岩体压密程度较高；3.4 m以后，超声波传播速度为1 410～1 684 m/s之间，平均为1 612 m/s，说明此段范围围岩处于弹塑性区域。据此可判定中央辅助运输大巷1-1钻孔处巷道围岩松动圈的范围为2.9 m。中央辅助运输大巷1-2号钻孔在距离巷帮2.7 m范围内，超声波波速1 226～1 581 m/s之间波动，平均为1 404 m/s；在2.7m以后，超声波传播速度明显增大，维持在1 395～2 028 m/s之间，平均为1 720 m/s，增长了22%，说明此段范围围岩处于弹塑性区域。据此可判定中央辅助运输大巷1-2钻孔处巷道围岩松动圈的范围为2.7 m。同理，可判定中央辅助运输大巷2-1、2-2、3-1、3-2钻孔处巷道围岩松动圈的范围分别为2.7 m、2.7 m、2.7 m、2.8 m。综上所述，玉溪煤矿中央辅助运输大巷围岩松动圈的范围为2.7～2.9 m。

3 巷道松动圈数值模拟

现场测定岩石巷道松动圈的过程中，只能得到岩石巷道松动圈的具体破坏范围，并不能得出巷道形状变化和巷道深度变化条件下岩石巷道松动圈的变化规律，加之现场测试成本较大、工程量较大、施工周期长，因此本文运用数值模拟进行验证分析，以得到不同巷道形状和不同巷道深度条件下岩石巷道松动圈的变化规律，为玉溪煤矿施工设计提供技术指导。

3.1 数学模型的建立

在巷道岩体在形成过程中，由于地质条件的影响，存在层理和节理的非均质结构，故巷道岩体为一种非均质、非连续以及周围应力条件复杂的一种介质。但在研究过程中，选取的是较大的区域，可以近似地看作可向同性的均质体。为使问题简化，做出如下假设：

1) 巷道围岩为理想的弹塑性体，满足 Mohr-Coulomb 屈服准则；

2) 各个岩层均为层状分布，岩体为均质的各向同性体；

3) 因岩层倾角较小，为方便计算按水平岩层考虑；

4) 不考虑地下水渗流的影响。

3.2 物理模型及边界条件的建立

选择玉溪煤矿中央辅助运输大巷为岩石巷道的工程背景，选用的岩石破坏准则为Mohr-Coulomb准则，在所建模型上部加载对应埋深为的地应力(岩石密度均值为2 500 kg/m3)。模型左右采用滚动边界条件，下部采用固定边界条件，如图4所示。

图4 物理模型图

根据玉溪煤矿中央辅助运输大巷顶底板岩性的实际情况，该模型岩石巷道位于砂质泥岩中，顶板岩性为泥岩、细粒砂岩和泥岩，底板岩性为粉砂岩、细粒砂岩。通过查阅玉溪煤矿相关报告以及相关研究成果，得到具体力学参数如表1所示。

表1 模型参数

3.3 不同埋深条件松动圈数值模拟

巷道周围岩体开挖前的初始地应力由巷道埋深所致，初始地应力决定了巷道开挖后的稳定情况。通过现场情况，选择断面积为20 m2，埋深为260 m、460 m、660 m、860 m的情况，研究不同埋深对巷道松动圈分布的影响。通过模拟可以得到巷道围岩分别在埋深为260 m、460 m、660 m、860 m 的松动圈(破坏区)分布图，如图5所示。

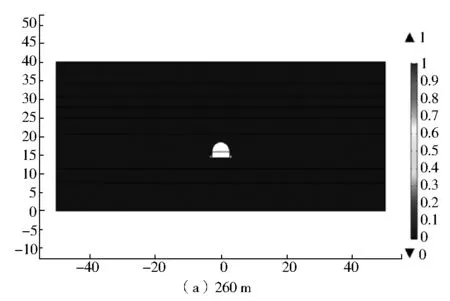
由图5(a)可以看出，巷道周边的松动圈是以巷道中心为对称轴左右对称分布的，在巷道的底角位置出现了0.5～0.6 m小范围的松动圈，在巷道两侧以及巷道顶底板未出现明显的松动圈分布。这是由于拱形巷道底角尖锐的角度形成应力集中，故松动圈优先在巷道底角位置出现。

由图5(b)可以看出，巷道周边的松动圈以巷道中心为对称轴左右对称分布的。相对于260 m的巷道，巷道两侧和巷道底角位置松动圈的范围明显增大。在巷道底角松动圈为1.6 m左右，在巷道两侧位置上松动圈的范围为1～1.2 m，巷道斜上方位置松动圈分布相对较小。这是由于随着埋深的增加，巷道所受的地应力增大，导致松动圈在巷道底部继续延伸，同时地应力达到了巷道所在岩层的破坏强度，故松动圈在巷道两帮开始逐渐发育。

由图5(c)可以看出，巷道周边的松动圈以巷道中心为对称轴左右对称分布，且在形状上表现为“蝴蝶形”。相对于460 m的巷道，在巷帮、巷道底角以及巷道斜上方位置松动圈的范围明显增大。在巷道底角位置松动圈为6.8 m，增加了2.5倍。在巷道两帮位置上松动圈范围为3 m，增加了1.5倍。巷道斜上方位置松动圈分布为6.3 m。由于地应力的增大，松动圈在巷道周围持续发育。当最大主应力与最小主应力比值η>3时，巷道斜上方发育较为明显，巷道底角和巷道两帮的松动圈继续延伸，最终松动圈在形状上表现为“蝴蝶形”分布。

由图5(d)可以看出，巷道周边的松动圈以巷道中心为对称轴左右对称分布的。相对于660 m的巷道，在巷帮、巷道底角以及巷道斜上方位置松动圈的范围均明显增大。在巷道底角位置松动圈为11 m，增加了0.6倍。在巷道两帮位置偏上的松动圈的范围为15～16 m，增加了4倍左右。在巷道两帮位置偏下的松动圈范围为16～18 m，增加了5倍。巷道斜上方位置出现的松动圈分布为8.6 m，增加了0.4倍。这是由于随埋深的加大，巷道承受极高的地应力，巷道所在岩层强度相比于地应力较小，导致松动圈在巷道两帮发育十分明显。不同深度下松动圈的范围数据参数如表2所示。

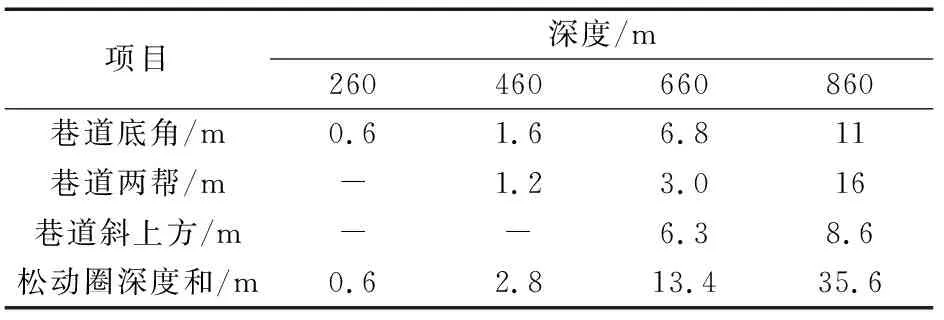
表2 不同深度下岩石松动区的范围

通过以上分析，随着埋深的增加，巷道两帮、巷道底角以及巷道斜上方位置的松动圈的范围逐渐变大，且在巷帮的增加速度大于在巷道底角以及巷道斜上方位置的增加速度。随着埋深的增加，巷道顶板和巷道底板均没有出现明显的松动圈。

为了进一步研究松动圈的范围与埋深之间的关系，取3个区域(巷道底角、巷道两帮、巷道斜上方)松动圈的最大影响范围进行累加，得到巷道松动圈深度和随埋深的变化规律，如图6所示。分析图6可得，松动圈深度和与埋深之间满足的指数关系，故随着埋深的增加，巷道松动圈的范围逐渐增加，且增加的速度越来越快。

图6 松动圈深度和随埋深的变化规律图

4 结 语

1) 随着深度增加，当最大主应力与最小主应力比值η>3时松动圈分布大致呈“蝴蝶形”分布，且巷道设计时断面越“圆滑”，其松动圈的范围就越小，相对于具有尖锐角度的巷道具有更好的稳定性。

2) 随着埋深的增加，巷道松动圈的范围逐渐增加，且增加的速度越来越快，并且松动圈的范围与埋深之间满足指数关系。

3) 根据玉溪煤矿的实际情况(埋深660 m)，经现场测试和数值模拟得到断面积20 m2，断面形状为拱形的中央辅助运输大巷(岩巷)围岩松动圈的范围为2.7～2.9 m。

4) 由于玉溪煤矿的顶板和底板岩性的特殊性，巷道底板以下10 m处的岩石强度大于其他岩层，从而限制了底部拐角处的岩石松动圈的延深发育，今后研究应针对不同的顶板和底板岩性条件进行进一步的分析和讨论。