搬运机器人用异步电机自抗扰控制策略研究
2022-02-17林立柏明科林喜斌
林立 ,柏明科,林喜斌
(1.多电源地区电网运行与控制湖南省重点实验室,湖南邵阳,422000;2.邵阳学院 电气工程学院,湖南邵阳,422000;3.邵阳资水科技公司,湖南邵阳,422000)
0 引言
搬运机器人具有工作效率高、负载大、工作场合广泛等特点,在汽车行业、货物运输、电子行业、船舶行业等得到了广泛的应用[1]。异步电机具有结构简单、成本低廉、制造方便、运行可靠、坚固耐用、运行可靠等优点,可以应用于比较恶劣的环境,在工业应用场合得到了非常广泛的应用[2]。矢量控制的引入使异步电机定子电流成功实现了解耦,让异步电机的调速性能媲美于直流电机的调速性能[3,4]。异步电机现代控制策略如滑模变结构控制[5]、自适应控制[6]、预测控制[7]、内模控制[8]等控制策略有效的提高了电机控制系统性能。但是,滑模变结构控制存在“抖振”现象,在低速时,会产生很大的转矩脉动;内模控制器的固定时间常数在鲁棒性和快速性存在矛盾;自适应控制算法复杂;预测控制算法存在预测精度低、反馈修正方法单调、滚动优化策略少等问题[9]。而自抗扰控制器不依赖于系统精确的数学模型模型,通过扩张状态观测器对系统的内外扰动进行实时估计并予以补偿,使电机调速系统得到更好的动态性能和鲁棒性能,在电机控制领域中得到了广泛的应用。
本文分析了异步电机的动态数学模型,阐述了自抗扰控制理论,设计并搭建了一种转速环为自抗扰控制的搬运机器人异步电机矢量控制系统。并将基于自抗扰控制的异步电机矢量控制系统进行了仿真与实验验证,与传统PI控制的异步电机矢量控制系统比较,基于自抗扰控制的异步电机调速系统的抗负载干扰能力和动态稳定性能都得到了提升,解决了PI控制系统中超调与快速性的矛盾。
1 异步电机动态数学模型
根据矢量控制理论,异步电机的动态数学模型可以用以下四阶非线性微分状态方程组表示:
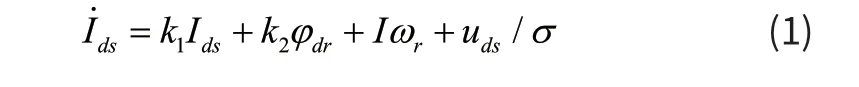
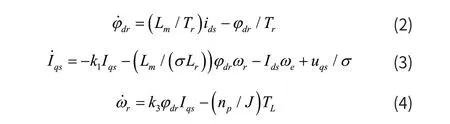
式中:
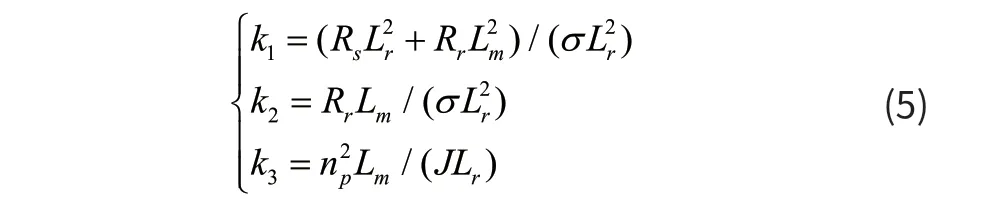
Lm为定转子间互感,Lr为转子电感,Ls为定子电感,ωr为电机转子转速,Tr为时间常数,Ids,Uds为d轴上的电流分量和电压分量,Iqs,Uqs为q轴上的电流分量和电压分量,np为极对数,φdr为转子磁链d轴分量,J为转动惯量,Rs和Rr为定子电阻和转子电阻。由式(1)和(3)可知,定子电流并没有实现完全解耦,IdsIqs仍然存在着交叉耦合,这对异步电机控制系统高性能的实现增加了一定的难度。ADRC的核心思想是将所有能影响系统的因素归结于“扰动”,主动从被控制对象中提取“扰动”信息,通过控制信号来消除扰动的控制方法,这样就可以不依赖于系统精确的数学模型就能实现系统高性能控制。通过分析ADRC的原理,将异步电机调速系统中的所有内在因素和外界因素总归结为系统的总扰动,这样就可以把转子磁链与转矩之间的耦合看作为电机调速系统的内在因素,利用扩张状态观测器进行观测,并实时进行补偿,使异步电机调速系统的的动态性能和鲁棒性得到了提高。
2 异步电机转速环自抗扰控制器的设计
自抗扰控制是一种针对非线性、不确定性系统的控制方法,由跟踪微分器(Track Differentiator,TD),扩张状态观测器(Extended State Observer,ESO),非线性状态误差反馈控制率(Nonlinear State Error Feedback Control Rate,NLSEF)三部分组成[10,11]。由式(4)转速方程式可得:
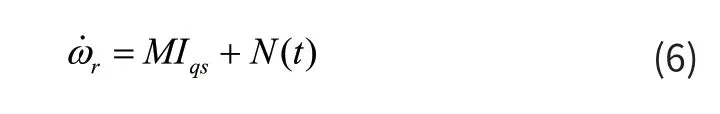
式中:M=K3φdr,N(t) = (np/J)TL,负载转矩TL与转动惯量J会根据异步电机工作的状态不同而发生变化,从而较大程度的影响了电机的转速性能。故可将N(t)视为扰动,利用扩张观测器进行实时估计并予以补偿。图1为自抗扰控制器的原理框图。
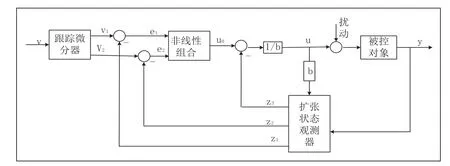
图1 自抗扰控制器的原理框图
跟踪微分器(TD)是为了防止目标值突变而安排的过渡过程,它能有效的避免输入量跳变,有效的解决了传统PI控制快速跟踪和超调之间的矛盾。离散形式的非线性微分跟踪器为:
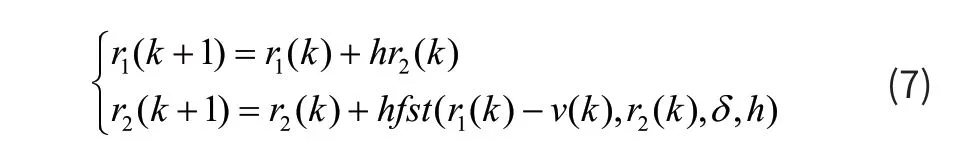
式中,v(k)为k时刻的输入信号,δ为决定跟踪快慢的参数,fst()函数为最速控制综合函数。
非线性控制率(NLSEF)的两个输入分别是e(1e1=v1-z1)、e2(e2=v2-z2),其输出是u0,u0并没有叠加系统总扰动补偿,它只是NLSEF的输出,并不是系统的最终输出。系统的最终输出是直接作用到被控对象的量u(u=u0-z3/b)。本文使用的的NLSEF公式如(8)所示:
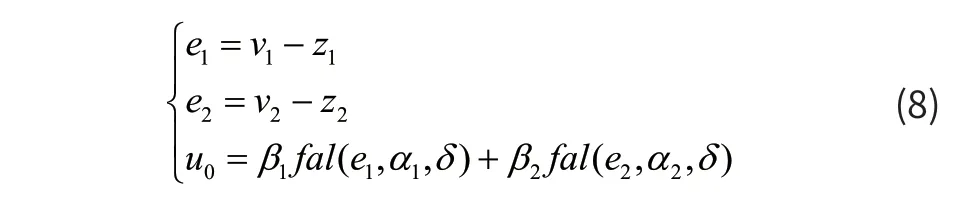
其中 0<α1<α2<1。
由图1可以看出扩张状态观测器(ESO)的输入有两个,分别是反馈值y和输出值u *b(b被称为补偿系数)。z1、z2、z3为ESO的三个输出,z1的数值是跟随着输出y的,z2是跟随y的微分的,z3是系统扩张的一个状态,它对系统的总扰动进行观测并进行一定的补偿,也是自抗扰控制器最核心的部分。ESO的数学表达式如(9)所示:
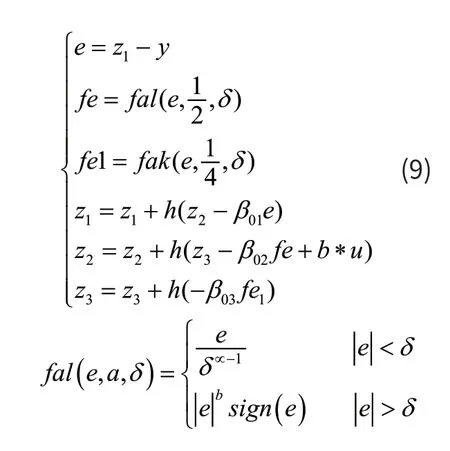
3 基于自抗扰控制的异步电机矢量控制系统的设计
异步电机的动态数学模型中许多变量存在着耦合,提高了其获得高动态调速性能的难度。将异步电机矢量控制系统中速度环采用自抗扰控制,可以把系统的交叉耦合、参数和负载变化等统一视为系统的“扰动”,通过扩张状态观测器(ESO)对这一系列“扰动”进行实时观测并补偿,跟踪微分器(TD)对给定信号的跟踪和微分信号的获取,非线性状态误差反馈控制率(NLSEF)生成控制量,为异步电机高动态调速性能的实现奠定了基础。自抗扰控制器继承了经典PID控制器的精华,对被控对象的数学模型几乎没有任何要求,解决了PI控制系统快速性与超调之间的矛盾。图2为基于ADRC的异步电机矢量控制原理框图。
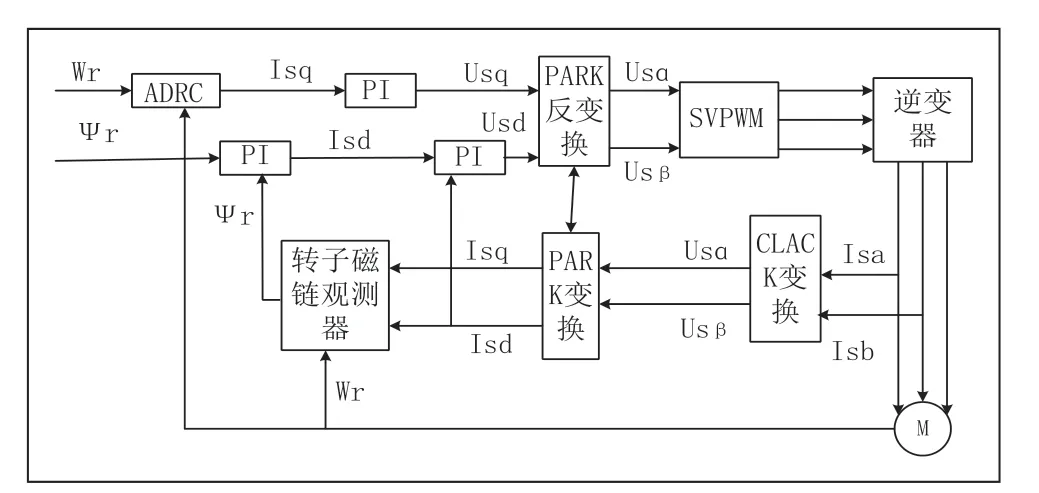
图2 基于ADRC的异步电机矢量控制原理图
4 仿真研究
为了验证采用ADRC的异步电机矢量控制系统的动态性能和鲁棒性能。本文在Matlab/Simulink上分别对转速环采用PI控制转速环采用ADRC控制的异步电机矢量控制系统进行了系统仿真模型的搭建,采用ADRC的异步电机矢量控制系统仿真框图如图3所示。仿真时电机的额定参数为:PN=3kW,UN=380V,IN=6.5A,fn=50HZ,RS=0.435Ω,Rr=0.816Ω,J=0.18kg.m2,nP=2,Lm=0.069H。仿真时两系统工况相同,给定转速为500r/min,在1s时,负载由空载突增到30N*m。由图4可知,采用自抗扰控制器的异步电机矢量控制系统动态响应速度更快,在0.15s时速度就达到了稳定,而基于PI控制器的异步电机调速系统存在着超调问题,直到0.3s时才达到稳定,在1s加载时,ADRC控制转速波动很小,而PI控制转速波动较大且持续时间较长。
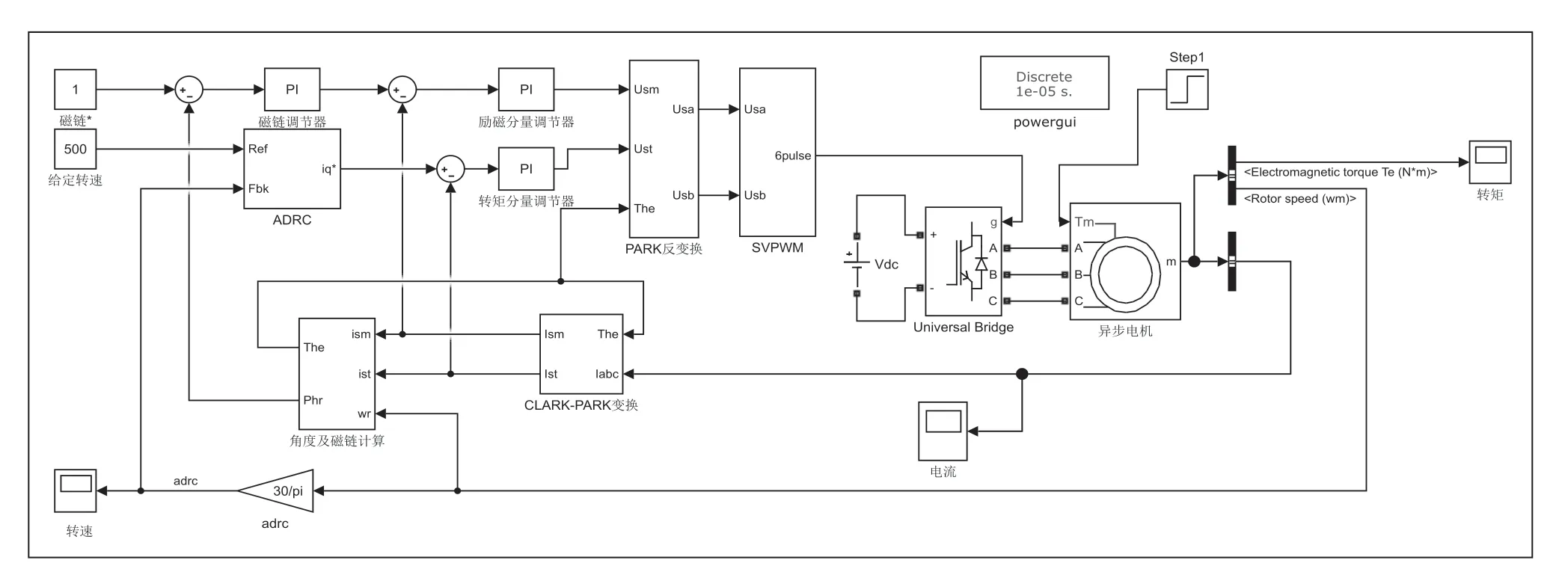
图3 采用ADRC的异步电机矢量控制系统仿真图
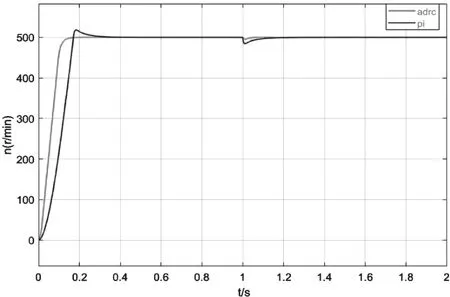
图4 转速波形对比
5 实验研究
图5为异步电机矢量控制系统采用ADRC控制的实验平台,该平台由A,B,C,D,E,F,G七部份组成。其中A为电源模块,B为TMS320F28335芯片,C为仿真器,D为三相异步电机,E为磁粉制动器,F为编码器,G为上位机,并通过编码器对异步电机的转速进行实时监测,通过电流传感器检测异步电机三相电流运行的状态。
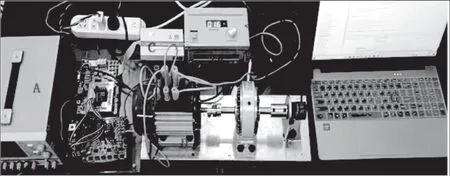
图5 实验平台
实验时电机的额定参数为:pN=40W,UN=380V,IN=0.2A,fN=50Hz,在该平台上,分别对采用ADRC控制器的异步电机矢量控制系统与采用PI控制器的异步电机矢量控制系统进行实验,并将它们的转速波形进行了对比,如图6和图7所示。实验时两系统工况相同,给定转速为500r/min,同一时间突加相同负载,从图6和图7可以得到:ADRC控制器相对于PI控制器,突加负载时,电机转速变化少,电机转速稳定时间快,很快就能达到动态平衡。
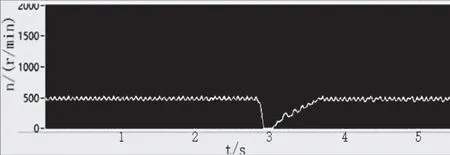
图6 采用PI控制器的转速响应
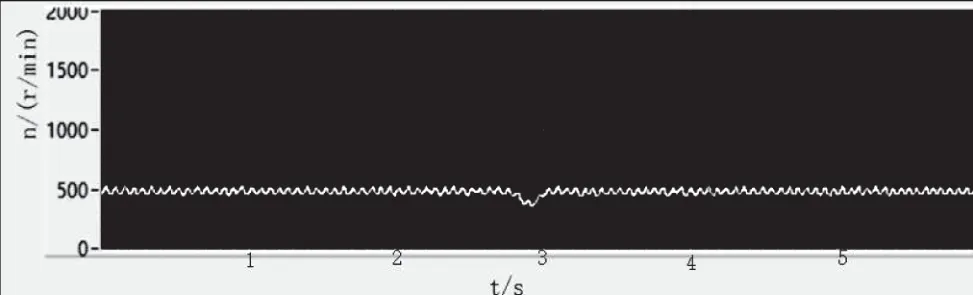
图7 采用ADRC控制器的转速响应
6 结论
本文将自抗扰控制用于异步电机矢量控制系统中的转速环,并对其进行了仿真与实验。仿真和实验结果表明:相对于传统PI控制,基于自抗扰控制的异步电机矢量控制系统的快速响应能力及抗负载干扰性有了一定的提升,且系统的鲁棒性能较好,超调量少,解决了PI控制中快速性与超调的矛盾。
