私法制度中的代数算法黑箱及其应对

陈 醇

多数判决书需要在其判决结果中给出具体的数量。这些数量是根据什么算法得出的？近年来，法学界日益重视人工智能及其算法在司法裁判中的应用，并已经形成了相当程度的共识。成文法国家的法律规范是司法裁判的基础。在这种背景下，如果仅仅只重视法律规范之外的算法问题，而不重视对现行法制度中算法的研究，就可能形成本末倒置的现象。本文努力将算法思维引入私法的规范研究，这在向来重视定性研究的私法领域，或许是一种新的尝试。

一、指导性案例所显示的代数算法黑箱

在考察我国私法制度与相关判决书的算法之前，有必要先对算法等基本概念及其类型进行一个简单的回顾与考察，以便后文能有较为精确的阐述。

(一)从算法到代数算法黑箱：概念界定

算法有多个不同的概念。算法一词是由阿拉伯著名数学家阿尔哥里兹米的名字演变而来，因为他给出了自然数运算的法则。(1)参见杨东屏、李昂生：《可计算性理论》，科学出版社1999年版，第1页。“一般认为第一个不可忽视的算法是欧几里德(Euclid)的计算最大公约数的算法。对于算法自身的研究要回溯到9世纪的波斯数学家Al-Khowarazmi，他的著述还把阿拉伯数字和代数引入了欧洲。”(2)[美]拉塞尔、诺文：《人工智能：一种现代方法》，姜哲等译，人民邮电出版社2010年版，第8页。这说明算法起源于算术。“所谓算法(algorithm)就是定义良好的计算过程。”(3)[美]科曼等：《算法导论》，潘金贵等译，机械工业出版社2006年版，第3页。算法是一组逐步执行的指令，非常机械地执行，以便达到一些预期的结果。(4)See Susan Nevelow Mart, The Algorithm as a Human Artifact: Implications for Legal Research, Law Library Journal, Vol.109, No.3, 2017, p.392.综合既有算法概念，可以认为，算法是根据一定的数据输入通过良好的计算过程计算出想要结果的方法。

算法可以分为不同的类别。第一，代数算法与几何算法。数学可以分为代数与几何，相应地，算法也可以分为代数算法与几何算法。当今算法多综合了代数算法与几何算法。第二，机器算法与人工算法。根据计算者的不同，可以将算法分为机器算法与人工算法。(5)See Karni Chagal-Feferkorn，The Reasonable Algorithm, University of Illinois Journal of Law, Technology and Policy，Vol.2018, No.1, 2018, p.117.机器算法可以完成非常复杂而繁琐的计算，而人工算法一般只能完成相对简单的计算。根据机器算法的难度，可以将机器算法再分为深层算法(深度神经网络)和浅层算法(如支持向量机)。(6)See Yavar Bathaee, The Artificial Intelligence Black Box and the Failure of Intent and Causation，Harvard Journal of Law & Technology，Vol.31, No.1, 2018, p. 895.第三，根据算法所依据材料的不同，可以将算法分为基于规则的算法、依据开放性概念的算法、依据案例的算法、混合算法、依据法律知识的算法五种。有学者将计算机算法中的推理分为规则推理、概念开放性推理等五种推理。(7)See Edwina L. Rissland, Artificial Intelligence and Law: Stepping Stones to a Model of Legal Reasoning, Yale Law Journal, Vol.99, No.6, 1990, p.1966.

除了上述分类之外，还可以根据算法的透明度将之分为透明算法与黑箱算法。透明算法是指计算基础(输入材料)、计算过程与计算结果具有透明度的算法。黑箱算法是指计算基础、计算过程或计算结果不太透明或不透明的算法。“术语‘黑箱’是一个有用的比喻，因为它有自己的双重含义。它可以指一种记录设备，如飞机、火车和汽车上的数据监控系统。它也可以指一个运作方式神秘的系统；我们可以观察它的输入和输出，但我们无法知道其中一个是如何变成另一个的。”(8)Frank Pasquale, The Black Box Society: the Secret Algorithms that Control Money and Information，Harvard University Press, 2015, p.3.于此，我们将不能知悉算法的计算基础、计算过程或计算结果的现象称作算法黑箱。

所谓代数算法黑箱是指私法制度中代数算法规范中的算法黑箱。对此概念说明如下：第一，该概念以代数算法规范为基础，仅指上述法律规范中的算法黑箱。私法制度中存在各种算法规范，包括定量方面的规范即代数算法规范(下文简称代数规范)，也包括定性方面的法律规范即几何算法规范(定性规范)。第二，代数算法黑箱与其中算法的正确性是不同的概念，因此，代数算法黑箱并不一定意味着其结果错误。在法律规范及其适用之中，计算的透明度与计算的正确性是两个不同的要求，因此，不能因为计算结果的正确性或合理性而认定算法黑箱的正确性或合理性。换言之，私法试图限缩代数算法黑箱，并不仅仅出于结果公正的考虑，更多的是基于过程公开与公正的考虑。第三，无论是简单的代数算法黑箱还是复杂的代数算法黑箱，二者同样值得重视。早期的算法就是算术，其后，算术逐渐发展为代数，随着数学与计算机科学的发展，算法也越来越复杂。指导性案例中的算法往往是简单算法，而法律人工智能领域则多运用复杂算法，但二者相关的黑箱同样值得重视。第四，代数算法黑箱可能是一种或多种算法黑箱。算法黑箱包括算法基础、过程或结果三种代数算法黑箱情形，相应地，代数算法黑箱也可能存在上述一种或多种情形。

(二)代数算法黑箱导致的算法瑕疵：以指导性案例的判决书原文为例

截止2021年10月15日，最高人民法院共公布了29批165个指导性案例，其中有78个民商事案例。笔者对这78个案例的判决书原文进行了整理，发现其中22个民事判决书存在算法上的争议，并因为所援引法律规范的代数算法黑箱而存在算法瑕疵。

案例编号所争议的算法及其焦点所援引私法规范及其代数算法黑箱法官的代数算法评论:文书中的主要算法瑕疵8号公司僵局的算法;“二分之一”是否包括本数《公司法》)第183条及其解释;无算法给出了公司僵局的算法创造了表决僵局的算法,但没有给出“长期”的算法15号债权数额的算法;多笔债权的数额、关系及其总和的算法《合同法》第60条、第80条、第82条等;仅第159条有单个债权数额的算法且不太明确,无多个债权数额、关系、总和等的算法虽然混乱,但仍然计算了一些债权的数额逐个计算各个债权数额及其总额,计算步骤不明,出现了难以理解的数据,计算过程不明确23号“十倍赔偿金”的算法;十倍赔偿的算法《食品安全法》第96条;有计算方法但参数不太明确将购物目的排除于“十倍赔偿金”的算法之外论证了购物目的不是算法的参数11个侵权案侵权赔偿损失数额的算法;赔偿数额的算法如指导性案例第30号援引了《关于审理商标民事纠纷案件适用法律若干问题的解释》第10条、第12条等;均没有算法指出了所考虑的参数,估计了赔偿损失的数额指出了“酌情”考虑的参数,不考虑参数的量、权重等,没有计算公式51号违约赔偿损失数额的算法;赔偿数额的算法《经海牙议定书修订的华沙公约》第19条、第20条等;无明确算法得出了赔偿损失的结果有计算结果无计算过程53号借款合同债务的算法;罚息、复利与律师代理费的算法《合同法》第60条第1款、第107条等;仅第207条规定了按约定或规定支付逾期利息;无具体算法在忽视重要的参数及其数量的前提下,仍然给出了结果没有考虑上述费用总和的计算及其意义(违约金过高、超越赔偿损失的范围等),算法论证不全面68号关联关系的算法;债权总额与绝对控股权的算法《公司法》第217条;该条没有算法从债权总额与绝对控股权之上计算出关联关系有些有计算过程,有些没有,计算过程不完整72号违约金与债权数额的算法;算法及其选择依据《合同法》第9条、第44条、第114条及其解释等;以上条款有违约金上限及其调整规范,无违约金与债权数额的算法根据部分数据算出了违约金与债权数额计量单位有明显错误,没有论证算法选择的标准,计算过程不完整、计算结果不明确73号优先受偿权数额的算法;优先受偿权数额的算法《关于建设工程价款优先受偿权问题的批复》第1条、第4条;无优先受偿权具体数额的算法将损失与利润等排除于优先受偿权之外没有论证优先受偿权为什么不包括损失与利润,算法依据、计算过程与结果均不明确107号违约赔偿损失数额的算法;数量多少的争议《联合国国际货物销售合同公约》第74条、77条等;有赔偿损失的数量范围,没有具体算法根据部分数据给出了赔偿损失的数额没有具体债务计算步骤、公式,算法混乱,计算过程不明确、不连续111号损失赔偿额的算法;复利、罚息与违约金的算法《合同法》第114条及其解释等;后者规定了违约金的上限,但没有违约金的算法将复利、罚息作为违约金且算出了违约金与实际损失的比例算法依据与过程不太明确

(说明：“11个侵权案”是指指导性案例29、30、45、47、49、80、82、83、84、86、161号；表中所引法律规范均为判决时有效的法律规范，一些条款已经被现行法所修改。)

从以上案例可以看出，代数算法黑箱导致了指导性案例的各种算法瑕疵。在第15号指导性案例(简称案15，其他简称类推)中，因为缺乏相应的算法规范，法官处理多个合同及其债权债务账册的数据时缺乏法律依据，无力进行有序的、分步骤的计算。一审法院只审理了债权债务中的“73笔，涉及金额仅717万元”，未提供其余纠纷的数据及其算法；二审法院也对算法一笔带过，没有说明其中各个数额从何而来、证据是什么、计算公式如何。案68也涉及复杂的债权债务与股权计算，但也因为代数算法黑箱而缺乏计算过程。“11个侵权案”揭示了类似的代数算法黑箱。以案30为例，一审法院“综合考虑天津小拇指公司与天津华商公司的侵权行为的性质、期间、后果以及二权利人为制止侵权支出的合理开支等因素，酌情确定本案的赔偿数额为50000元”；二审法院“综合考虑杭州小拇指公司企业名称的知名度、天津小拇指公司的侵权情节及损害后果等因素，酌情确定天津小拇指公司的赔偿数额为30000元”。所援引法律规范仅仅列出算法所考虑(“酌情”)的参数而没有规定侵权责任的具体算法，将之留给法官自由裁量，上述文书也无力列出算法，而直接给出了估算结果，如何估算不得而知。在案53与案111中，法律规范没有涉及罚息、复利等算法，文书也缺乏算法。当存在两种或多种不同的算法之时，所援引法律规范没有规定算法选择的条件，文书也非常随意。如案72，一审法院的两个算式是：“2014年10月1日至2014年11月21日的同期同类贷款年利率为6.55%，361398017.78元×(6.55%÷365)×51天=3307534.38元；2014年11月22日后的同期同类贷款年利率为6.15%，361398017.78元×(6.15%÷365)×98天(计算至2015年2月28日)=5967522.85元。”(9)作者认为这两个算式的单位有误，结果也不正确，应当分别是：361398017.78×(6.55%÷365)×51=3307534.46(元)；361398017.78×(6.15%÷365)×98=5967522.89(元)。二审法院没有论证上述算式的依据，没有指出计算单位的错误，而认定当事人“尚未足额支付合同约定的361398017.78元首期购房款”，缺乏算法及其理由。案例所援引法律规范的表述多数是文字表述，相应地，只有极少量(共2个)案例运用了计算符号。在上述78个民商事判决书中竟然没有出现一个完整且正确的代数表达式。

(三)本文的问题与相关理论回顾

面对私法制度的代数算法黑箱，本文拟讨论的问题是：在人工智能时代，私法应如何应对上述黑箱？成文法国家对任何问题的解决，首先仰赖于完善的法律规范体系，法律适用必须以此为据。因此，对指导性案例中算法瑕疵的应对，均应从代数规范这一源头着手。

近年来，国内人工智能的研究日益繁荣，却鲜有算法规范包括代数规范方面的讨论。有学者认为，网络社会中的人越来越受到算法的规训，法律应当反过来规制算法；(10)参见姜野：《算法的规训与规训的算法：人工智能时代算法的法律规制》，载《河北法学》2018年第12期。“算法即法律”的说法是彻底错误的，算法必须受制于法律。(11)参见陈景辉：《人工智能的法律挑战：应该从哪里开始?》，载《比较法研究》2018年第5期。进而有学者认为：“算法规制应采取场景化的规制路径，根据不同场景类型对算法采取不同的规制方式。”(12)丁晓东：《论算法的法律规制》，载《中国社会科学》2020年第12期。另有学者认为应当借鉴美国法经验，对算法歧视进行司法审查；(13)参见郑智航、徐昭曦：《大数据时代算法歧视的法律规制与司法审查——以美国法律实践为例》，载《比较法研究》2019年第4期。或主张“发挥人工智能对司法的优化重塑效应”。(14)马长山：《司法人工智能的重塑效应及其限度》，载《法学研究》2020年第4期。以上五个文献中，前三者仅仅将算法作为法律的调整对象，后二者仅将算法作为司法审查的对象或推动力量，没有考虑算法对法律的影响尤其是如何将算法引入法律规范等问题。

一些学者意识到了算法与法律规范的联系，却还不够明确。有学者建议将实体法规范、构成要件以及要件事实作为机器学习的“影响因子”，以形成要件事实型人工智能民事判决。(15)参见高翔：《人工智能民事司法应用的法律知识图谱构建——以要件事实型民事裁判论为基础》，载《法制与社会发展》2018年第6期。该论强调实体法对机器算法的影响，但没有意识到算法规范及其与机器学习的关系。有学者认为，算法给法律的启示是重视信息成本、确定合理的类型化程度等。(16)参见蒋舸：《作为算法的法律》，载《清华法学》2019年第1期。该观点只在法理层面讨论算法对法律的影响，没有涉及算法与法律规范的具体关系。有学者针对算法黑箱、算法错误与“算法自主”现象，认为应当探索法律代码化、规则精细化。(17)参见马长山：《智能互联网时代的法律变革》，载《法学研究》2018年第4期。这一观点意识到了算法与法律规范的关系，但未能从算法规范的视角明确指出法律与算法的关系。另有学者讨论了法律算法化的条件等内容。(18)参见郑戈：《算法的法律与法律的算法》，载《中国法律评论》2018年第2期。该观点提醒人们注意法律与算法的关系，但尚停留于理论层面而未落实于规范。有学者认为应“将法律的原则和规则嵌入算法的模型和逻辑，使算法在执行过程中符合法律的要求”。(19)袁康：《可信算法的法律规制》，载《东方法学》2021年第3期。从该观点或可推知算法应当嵌入法律的理念，但与算法规范方面的讨论尚有很大的距离。有学者强调：“法治必须学会对接人工智能和算法。”(20)蔡星月：《算法正义：一种经由算法的法治》，载《北方法学》2021年第2期。该文未能从算法规范之上来谈论二者的对接，忽视了法律规范在法治中的根本性地位。有学者强调了算法解释权的重要性及其治理路径。(21)参见张欣：《算法解释权与算法治理路径研究》，载《中外法学》2019年第6期。解释现实生活中的算法需要以法律规范为依据，在讨论解释权时还需要讨论算法规范。

国外学者对算法黑箱的讨论较多，其共同特点是以机器算法为重心且将算法黑箱归因于机器算法。如前所述，有学者指出了规则推理、概念开放性推理等五种机器算法模型。这是对机器算法的总结，它未能很好地思考如下问题：法律推理是否必须以法律规则或先例为基础？如果作肯定性回答，那么，这些推理模型或许首先应考虑法律规范与先例及其中算法的完善，其他推理模型应以此为基础。将算法黑箱怪罪于“机器的统治”，认为机器学习的模型不透明等；(22)See Emily Berman, A Government of Laws and not of Machines, Boston University Law Review, Vol.98, No.10, 2018, p.1284.或者认为算法透明化是克服算法黑箱的最好方法。(23)See Robert Brauneis, Ellen P. Goodman, Algorithmic Transparency for the Smart City, Yale Journal of Law and Technology, Vol.20, Iss.1, 2018, p.133.这类观点不无道理，但均忽视了机器学习的先天缺陷：所有的机器学习(无论其深度如何)均只是对既有法律资料的学习，在这些资料中，算法规范及其适用资料没有得到特别的重视，因而不能明确机器学习的重点。更重要的是，即使将算法规范及其裁判资料作为机器学习的重点资料，在上述二者还不完善的背景下，资料的缺陷必然会传导于以此为基础的算法之中。因此，将算法黑箱全部归因于机器算法，未免忽视了算法规范的根本性地位，也掩盖了算法规范中的黑箱。

二、私法制度中代数算法黑箱的成因

(一)希腊几何学对民法的深刻影响

要了解私法中代数算法黑箱的形成历史，必须从希腊几何学对私法制度的深刻影响及其后果开始。希腊数学主要是对初等几何的研究，它运用了公理法(即基于公理的逻辑推论)、演绎法、作图法等方法。(24)参见吴志勇：《古今初等数学思想》，天津大学出版社2015年版，第24页。这概括了希腊几何学的主要特征。“最好是选择尽可能少的公理，并使得其他命题能够从已经被接受的公理中演绎出来。”(25)[美]克莱因：《西方文化中的数学》，张祖贵译，商务印书馆2013年版，第60页。演绎法是希腊几何学对数学以及所有学科的最重要的贡献。(26)参见朱晓喆：《论近代民法的理性精神——以19世纪民法法典化为中心》，载《法学》2004年第5期。希腊数学偏向于几何，将定量计算视为缺乏教养的行为，认为演绎法是数学证明的唯一方法。(27)同前注，吴志勇书，第45-46页。

希腊几何思维对德国民法典产生了深刻的影响。第一，民法基本原则理论体现了希腊几何学中的公理法。德国民法理论与制度试图寻求万能的基本原则，隐含着希腊几何学的公理思想。第二，演绎法成为民法典与民法学的一般性方法。源于希腊几何学的演绎法，被大陆法系的民法学家出色地运用在法典化的理论研究中，并且通过法学家对制定民法典的影响，成为近代民法典的立法技术特征之一。(28)同前注，朱晓喆文。在民法适用之中，演绎法也成为基本的方法。第三，定性研究得到希腊几何学的营养而成为民法的基本研究方法。民法学者敌视以代数运算为特征的实证研究。“这种实证主义是法学的死敌。因为它将法学贬低为手工艺，故而法学须与其做殊死斗争。”(29)[德]耶林：《法学是一门科学吗？》，[德]贝伦茨编，李君韬译，法律出版社2010年版，第47-48页。

很多民法学家信奉希腊几何学的方法。著名法理学研究者认为：“自然法的基本原则是属于公理性的，就像几何学的定理一样”。(30)参见彼德·斯坦、约翰·香德：《西方社会的法律价值》，王献平译，中国人民公安大学出版社1990年版，第12页。让·多马宣称所撰写的《论自然秩序中的民法》对民法的编排遵从了几何学的秩序；拿破仑认为将法律化为简单的几何公式是完全可能的；萨维尼从法律的和谐之美出发，认定法学存在与几何学一样的公理和演绎方法。(31)参见张世明：《法学与数学的渊源关系》，载《中华读书报》2015年9月2日第13版。霍布斯也将希腊几何学方法应用于对法律现象的研究之中。(32)参见[英]霍布斯：《利维坦》，杨昌裕译，商务印书馆1985年版，出版说明。“在吾人之科学中，一切均取决于对于基本的原理原则的掌握，正是这些基本的原理原则，造就了罗马法学家们的伟伦不群。他们科学中的概念与公理，绝非任意妄断的产物……。除了在数学中，他们的全部运思模式均秉有他处所不及见的确定性。或许可以说，毫不夸张，他们对于自己的各种概念均作过精审的计算。”(33)[德]萨维尼：《论立法与法学的当代使命》，许章润译，中国法制出版社2001年版，第23页。萨维尼的上述议论，强调了公理法并将公理置于崇高的地位，他所说的“精审的计算”当然不是指代数计算，而是以公理为基础的演绎。

(二)私法对代数算法的疏离

在希腊几何学几乎垄断数学领域的历史背景中，代数的发展经历了一个颇有戏剧性的过程。9世纪阿拉伯数字和代数就引入了欧洲，但如前所述，长期以来，希腊几何学在欧洲数学领域占据着统治性的地位而使代数发展缓慢。不过，代数还是慢慢发展起来。17世纪的数学，“是代数与几何作用的完全颠倒。”(34)[美]克莱茵：《古今数学思想(第2册)》，石生明等译，上海科学技术出版社2014年版，第1页。柏拉图曾经说，上帝永远在进行几何化，但到了1900年左右，“数学已经算术化了”。(35)[美]克莱茵：《古今数学思想(第3册)》，刘东皋等译，上海科学技术出版社2014年版，第187页。算术是代数的初始形态，严格说来，那时的数学应当是代数化了。

与希腊几何学相比较，可以看到代数相对应的三个特征。第一，经验性。代数具有很强的经验性质，数量关系与运算法则是生活经验的产物与表达。早期的代数产生于经验，埃及和巴比伦数学就是如此。(36)同前注，克莱因书，第33页。代数的经验性与几何学的先验公理思想是相对立的。第二，归纳法。代数往往运用经验归纳法寻求一般规律。(37)参见[美]R·柯朗、H·罗宾：《什么是数学：对思想和方法的基本研究》，左平等译，复旦大学出版社2005年版，第16页。归纳法不同于演绎法，它具有描绘性质，所得出的公式可以揭示事物之间的相关性，但却并不一定能揭示事物之间的因果关系或定理之间的演绎关系。第三，定量计算。代数的定量计算不再局限于定性分析与作图法，其后代数日益复杂化，却始终没有改变其定量计算的特性。综上，代数以经验性、归纳法与定量计算为其思维特征，并以此区分于希腊几何学的公理法、演绎法与作图法。

将代数算法引入自然科学，这得益于伽利略等人的努力。伽利略强调了在自然科学中数学特别是代数证明的重要性。(38)参见[意]伽利略：《关于托勒密和哥白尼两大世界体系的对话》，周煦良等译，北京大学出版社2006年版，第160页。伽利略建立了推动近现代科学发展的有效方法——数学实验方法。(39)参见管锦绣：《伽利略科学方法与培根、笛卡尔哲学方法之比较》，载《武汉工程大学学报》2008年第6期。伽利略采用了数学定量方法。(40)参见李才华：《伽利略的科学方法》，载《合肥工业大学学报》2009年第3期。“以数学抽象为基础研究自然法则，和通过度量、计算及衡度手段证实数学抽象，显示了近代自然科学在诞生。”(41)[德]伽达默尔：《科学时代的理性》，薛华译，国际文化出版公司1988年版，第138页。他将代数算法应用于自然科学研究之上，引入了定量方法，这在方法论上实现了探寻自然知识的革命。从此之后，以代数算法为内容的定量研究日益受到推崇，最终成为自然科学领域公认的、最为基本的方法。

然而，私法却一直固守定性研究方法，而没有接受代数算法。这可能有三大原因：第一，罗马法奠定了私法的基础，但罗马人敌视代数算法，这形成了私法反感代数算法的传统。“罗马人无论何时未尝以数学和机械科学见长，这是人所熟知的。”(42)[德]特奥多尔·蒙森：《罗马史(第1册)》，李稼年译，商务印书馆2017年版，第499页。更为糟糕的是，罗马人只重视几何学，而将算术等其他“数学”等同于占星术，数学名声不好且被禁止，“数学和恶行禁典”一直到中世纪的欧洲仍被援用，“数学家”与“几何学家”的区分一直到文艺复兴之后的好久还保留着。(43)同前注，克莱因书，第203页。第二，私法学者对定性方法的推崇，导致了对代数算法的排斥。民法源于罗马法，但在数学史上，希腊几何学及其由此而形成的定性方法却是民法中数学思想的统治性思想。民法甚至被认为是“以概念计算”的法律思维方法。(44)参见[德]K·茨威格特、H·克茨：《比较法总论》，潘汉典、米健等译，法律出版社2003年版，第214页。但是，其中“计算”却不是定量计算，而是定性的演绎。第三，到代数算法被世人广泛接受之时，私法的定性方法已经成型，形成了自足性甚至封闭性。耶林说，“法学就是法律中的科学意识”，其科学意识表现为法哲学、法律史、法教义学三个方面。(45)同前注，耶林书，第86页。法哲学可以引导私法重视传统定性方法，法律史与法教义学则会引导人们保持上述私法传统，防范代数算法等思想进入民法科学之中。1900年代数算法才得到世人的公认，但是，此时德国民法典已经颁布。代数算法可能对刑法产生了一定的影响，其初步证据是刑法重视定量(量刑)，但私法从未将定量思想引入其中。(46)参见何柏生：《理性的数学化与法律的理性化》，载《中外法学》2005年第4期。

其后，法律经济学流派与实证主义法学流派重视代数算法，却并未能改变私法中的算法黑箱。波斯纳认为，不仅可以对法律案件的大量数据进行分析，法律规范本身也可以成为实证分析的对象，否则，是一种错误的认识。(47)[美]波斯纳：《法理学问题》，苏力译，中国政法大学出版社，第465页。法律经济学对英美私法影响巨大，但对大陆法系私法特别是德国民法理论与制度影响甚微。正如当年代数的繁荣没有影响德国民法一样，法律经济学也没有对德国民法产生实质性影响。法律的实证分析强调定量研究与实证的数据分析。其典型观点是：“有理无数慎谈学术。”(48)白建军：《法律实证研究方法》，北京大学出版社2008年版，导论部分，第12页。这种方法或许可以理解为伽利略实验数学方法在社会科学中的延伸。这一方法建议对法条文本进行实证分析。(49)同上注，白建军书，第4页。这种实证研究并不重视对法律规范或判决书中算法的研究，而只是以一定代数算法(如回归分析法)来研究法律规范与判决书等。研究私法的算法规范与以算法研究私法现象，毕竟不是同一件事情。以上两个法学流派均没有讨论私法制度中的算法规范及其适用，而将代数算法当作一种辅助性的研究方法。

(三)法律人工智能无力补救代数算法黑箱

当私法忽视代数算法且对代数的发展无动于衷的时候，以代数算法为主要算法的机器算法却已然蓬勃发展且势不可挡。但是，人工智能时代的机器算法无力补救私法制度中的代数算法黑箱。法律人工智能并不是对私法制度的质疑，它无意或者根本没有发现私法制度中的代数算法黑箱。法律人工智能只是在现有私法制度及其适用的基础上，通过各种方法包括机器学习来模仿甚至取代人脑的计算。无论机器学习如何优秀，它都只能学会既有私法规范及其判决中的算法，而很难避免私法制度中的代数算法黑箱。机器算法一般难以发现私法算法规范的缺陷，即使发现了上述缺陷，它也难以有所作为。到目前为止，人工智能司法与法律服务等方面的主张甚多，但还没见到人工智能立法方面的主张。如果机器学习能够进行私法的立法(即制定算法规范)，那么，人工智能就逾越了它的界限。

在法律人工智能无意且无力补救代数算法黑箱的同时，人工智能领域中的算法黑箱似乎正在日益加强。“依赖机器学习算法(如深度神经网络)的人工智能，可能与人脑一样难以理解。对于这些复杂的人工神经元网络的决策过程，目前还没有直接的方法来描绘。”(50)同前注⑥，Yavar Bathaee文，第892-893页。“有关底层代码结构的透明信息有时可能只与信息最初发布的精确时刻相关。”(51)Maayan Perel,Niva Elkin-Koren, Black Box Tinkering: Beyond Disclosure in Algorithmic Enforcement, Florida Law Review, Vol.69, No. 1, 2017, p.190.这强调了学习算法的黑箱特征。如果私法期待人工智能在其中广泛应用，那么，新的黑箱必然叠加于旧的黑箱之上。耐人寻味的是，代数算法黑箱是因为疏离代数算法而产生，而机器算法中的算法黑箱却是因为代数算法的深入运用而产生。无论这两种黑箱的解决方案如何，人们都能意识到上述两个黑箱的共同之处，那就是代数算法与私法制度的关系问题：代数算法与私法制度到底是什么关系？或许这就是代数算法黑箱的症结所在。

三、代数规范在私法制度中的重要地位

(一)代数规范的特征与类别

代数规范具有三个特征：其一，代数规范具有很强的经验性。以民事行为能力年龄标准为例，人类的智识发展并不是均质的，选取18岁作为统一的完全民事行为能力的年龄标准，既是经验的产物，也有一种统计数据上平均值的考虑。其二，代数规范往往会运用归纳法。代数规范中的数据与公式往往通过归纳法得到。例如，民法中的普通时效制度为3年，这是基于经验认为大多数权利适合于这样的时效，其中隐含了对平均值的归纳。在此方面，既不存在什么先验的公理，也无法根据什么公理推出结论。其三，代数规范以定量计算为标志性特征。这包括两层意思：一是代数规范中必然有数量，没有数量就不是真正意义上的代数规范。这为人们识别代数规范提供了一个简明的标志。二是代数规范之中必须存在计算公式。例如，公司法规定股东大会资本多数决的规范，就包含了一个公式：赞成票的数量大于等于总票数的二分之一或三分之二；(52)决议制度的计算公式，可参见陈醇：《算法视角下民法基本原则的体系理论》，载《法律方法》2019年，第27卷。破产法中的破产原因规范也包含了企业总资产小于其总债务(资不抵债)等公式，如此等等。

私法制度中存在各种类型的代数规范。从代数规范的内容之上，可以将之分为计算单位规范、数量规范、计算公式规范、计算步骤规范、极值规范(最大值与最小值)等。计算单位规范是规定私法制度中计算单位的法律规范，例如，“1次事故”中的“1次”的界定，就是单位界定问题，股权定量计算中的“1股”，也是重要的计算单位问题。数量规范则是关于数量大小多少的规范，例如，公司法所规定的公积金提取的比例规定，就是一个数量规范；计算公式是代数规范的核心内容，例如，证券法虚假陈述民事赔偿责任的计算公式就是计算公式规范；(53)《最高人民法院关于审理证券市场因虚假陈述引发的民事赔偿案件的若干规定》(法释[2003]2号)第29条至第35条规定了上述算法的公式，但是以文字而非代数式表达的。计算步骤规范是指规定计算过程次序的那些规范，例如，破产法中破产清算的顺序与公司法中的利润分配规则，就属于这一类规范；极值规范的目标是规定一些计算结果的上限或下限，例如，保险法中对保险公司负债总额上限的规定、对单个保险合同保险金额上限的规定，均属于这类规范。

除了上述常用的分类之外，还可以对代数规范进行学理分类。按照代数规范的复杂性，可以将之分为简明代数规范与复杂代数规范等。简明代数规范令人有一种亲切之感，但也容易受到忽视；保险费率的计算、操纵市场导致的损失数额计算等，是复杂的代数规范，为此，保险法与证券法等规定由精算人士或专门的清算结算机构完成。根据民商法的相对分野，可以将代数规范分为民法代数规范与商法代数规范，前者一般多为简明代数规范，后者多有复杂代数规范。近年来，复杂算法引入了证券法、商业银行法等诸多领域，出现了大量令人费解的代数规范。例如，商业银行法领域的流动性比率、杠杆率等方面的代数规范，就令人望而生畏。私法由于长期不重视数量与公式，很多代数规范以一般文字表述，要将之转化为代数算法表达，正如人们做数学应用题一样，还得完成数学建模过程。根据代数规范的强制程度，可以将之分为强制性代数规范与任意性代数规范，如此等等。

(二)代数规范的本质与功能

从质与量的关系看，代数规范是私法制度中的定量规范，它与定性规范一样，都是重要的法律规范。代数规范规定私法制度中的数量、计算公式等内容，是对私法制度中主体、权利、行为与法律责任的定量与计算。质与量是事物的双重属性，对任何事物的调整均离不开对其质与量的双重调整。这决定了二者地位的同等重要性。长期以来，私法重视定性分析与定性规范，而迄今为止没有明确的代数算法理论，这表现出其对代数规范的轻视。代数规范界定事物的量，其计算是数量变化的规则，它是私法必不可少的规范。

代数规范既有助于定性规范，也有其独立价值。正如开普勒所言：“只有当定性的确定被归结为定量的确定以后，才能在真实的外部世界中找到认知上的联系”；“定量的研究之对于人的探索，正如眼睛之对于探索色彩，耳朵之对于探索声音一样。”(54)[德]外尔：《数学与自然科学之哲学》，齐民友译，上海科技教育出版社2007年版，第173页。数量及其计算有助于揭示物质的多少及其变动规律，从而界定质的多少与变动规律，基于此，可以认为，代数规范是对定性规范的重要辅助。但是，代数规范不仅有辅助意义，它还有独立于定性规范的价值。代数是数学的一部分，其自身原理的独立性与独立的存在价值也是无可否认的。代数算法中的公式与定理，具有独立于事物性质的抽象性，它体现了代数算法的独立性与独立存在价值。代数规范也服从于代数的独特算法规律，这种规律不会因为应用于私法制度而改变，而私法制度只有遵守代数的算法规律，才有可能进行正确的计算。

代数规范与定性规范体现了不同的认识论。认识事物都离不开对其质与量的双重认识，但是，这并不意味着二者在任何场合下总是等量齐观。我们可以根据认识论重心的差异将之划分为两类：其一，以定性为主的认识论。该论主要从事物的性质上认识事物。在这种认识论中，定量因素只是认识论的参考因素或辅助性因素。这种认识论通过高度发达与复杂的定性来弥补其在定量上的不足，甚至只在无法运用定性方法描述事物的情况下才运用定量方法。在私法之中，概念法学是这样的认识论，它通过概念及其特征的详尽阐述来认识概念，其结果是从质上区分了大量的私法概念，而少有对量的依赖。其二，以定量为主的认识论。该论主要从事物的数量上认识事物。在这种认识论中，定性因素只是认识论的参考因素或辅助性因素。这种认识论通过高度发达与复杂的代数算法来减少其对定性的依赖，甚至只在无法运用定量方法描述事物的情况下才运用定性方法。这一认识论被广泛运用于人工智能之中。以识别垃圾邮件的算法为例，该算法不需要理解“电子邮件”、“赚取现金”、“白俄罗斯”或“垃圾邮件”等的性质，仅仅通过分析数据得出统计相关性,最终获得与同样聪明的人运用高阶认知过程和思考才能得出的结果。(55)Harry Surden, Machine Learning and Law, Washington Law Review, Vol.89, No.3, 2014, p.98.这就是以代数算法而不是以定性方法认识事物的例子。

代数规范与定性规范各有自己独特的优势、适用场景与不可替换性。在一个容易定性且不需要精确定量的领域，定性规范是适当的，也是足够的。在不容易定性的领域，定性规范就不太好用。此时，可以运用代数规范来解决这一难题。“算法设计的基本原则是以简驭繁，将质的困难转化为量的重复。”(56)王能超：《算法演化论》，高等教育出版社2008年版，第8页。在算法明确的领域，运用代数规范是合理的选择。同时，在需要精确性定量的领域，运用代数规范调整私法生活也是迫不得已的选择。因为定性规范无法达成数量与计算过程的精确性。在私法制度之中，与私人生活有关的大量数据及其计量，是不得不运用代数规范的领域。此时仅仅只适用定性规范，无法达成计算过程和数量的精确性。在适合于运用代数规范的领域，最好不要过度地运用定性规范，否则，不仅造成定性规范的篇幅过大，而且还有可能缺乏精确性。

(三)代数规范在算法时代的重要地位

发达的代数既为代数规范提供了可能，也对代数规范提出了要求。算术自古就有，但是，当今代数的繁荣却不是古代简单的算术可以比拟的。代数从初等代数到高等代数，各种算法日益发达。更为重要的是，计算机的发明、普及及其算法的日益发达，克服了人脑计算的难题，从而使代数达到了前所未有的高度。代数的深化使原先无法计算的事物成为可以计算的事物，可计算性的范围越来越大。原先认为只能运用定性规范进行调整的领域，现在如果愿意，或许多数能找到相应的代数算法来进行定量的调整。发达的代数为代数规范扩展其调整范围提供了可能。人工智能在大量领域的运用正在印证这样的观点：代数算法能够适用于原先认为不可计算的领域。与此相应，代数规范的调整领域必然会日益扩大。希腊几何学哺育了早期的私法，但私法的营养源不应当局限于几何学，而应扩展至同时代的所有数学领域。法律应随着数学技术的发展而发展，二者不应拉出更大的距离，更不应固守古代的数学观念而得少为足。代数应进入私法，现代代数算法应成为代数规范的技术支撑，代数规范应随着算法技术及其设备的改进而改进。

当今时代计算机的广泛运用，相应的代数规范也显现出独有的优势。代数算法以数量表达计算过程与结果，它具有演绎法所不具有的直观性，且展现出几何图形所不具有的准确性；代数算法能够描绘演绎的结果，也能够描述现象或经验，它能够运用于演绎法所不能运用的领域；代数算法能够计算与反映相关性，而不局限于演绎关系或因果关系，这扩大了数学的计算领域。“由于机器学习算法能够很好地检测出难以觉察的数据关系，因此，在法律案例中，有可能检测出某些变量与特定法律结果之间的模糊关联。”(57)同前注，Harry Surden文。这种关联性研究不反对演绎法，但它有助于挣脱演绎法的牢笼，达到启发私法思维的效果。“事实上，就是因为不受限于传统的思维模式和特定领域里隐含的固有偏见，大数据才能为我们提供如此多新的深刻洞见。”(58)维克托·迈尔-舍恩伯格等：《大数据时代》，盛杨燕等译，浙江人民出版社2013年版，第94页。在算法时代，计算机技术的发展使代数算法得到了长足的发展，代数算法的优势也因此日益显示出来。原先缺乏数据的领域因为计算机的大数据技术而得到了大量数据，因而得以算出其结果；原先因为智力与精力局限无法计算的领域，现在得益于计算机技术而可以进行重复机械的计算并得出结果；原先无法发现的相关性，现在因为计算机而得以发现，进而为挖掘新的因果关系提供了新思维。计算机技术是计算的技术，它为计算提供了更为广阔的空间与可能，这使代数算法的直观性、描绘功能、相关性挖掘等优势更为明显。私法制度中的大量代数规范，均是直观性的数量规范、描绘性的数量规范。例如，股票上市条件就隐含着相关性的算法经验，这些要件不是追求演绎法严密性的成果，而是实践经验与归纳法的成果。这些内容在一个以演绎法为主的时代是难以得到重视的，但是，在代数算法的优势得以显现的时代，这些代数规范的数量就可能增多，并得到更多的重视。

算法是以数据为原料的，大数据的出现也要求私法特别重视代数规范。代数算法既是大数据收集与储存的工具，也是大数据处理的工具，由此形成了一个大数据时代。“这种大数据能使我们对数据进行深度、系统性的分析，而采样几乎无法达到这样的效果。”(59)同上注，维克托·迈尔-舍恩伯格等书，第37页。没有代数算法，则无法收集、整理、储存与处理大数据，代数算法因而在大数据时代具有极为重要的地位。数据库及其共享对代数算法及其相应的算法规范提出了更高的要求。如何收集数据、如何整理数据、如何储存数据与如何处理大数据，这关系到私人的利益，私法应当进行调整。运用一定的代数规范调整大数据算法，这应当是现代私法在大数据时代的基本内容。大数据时代不应当仅仅被理解为一个数据时代，而应当被理解为一个数据及其算法的时代。私法应当适应大数据时代的要求而重视代数算法，由此完善相应的代数规范。

代数算法思维与以定量为主的认识论的普及，也要求私法适应私法生活的发展，重视代数规范。在古代社会，算术是少数人掌握的技术，多数人只有极为简单的算术常识。但是，现代社会，普通人的算法知识已经有了很大的提高。代数算法已经成为一种普通的思维方式，尽管其技术层级存在差异。同时，科技的发展为私人进行代数计算提供了方便。先是计算器与计算机可以辅助人们计算，后是网络可以共享计算过程与计算结果，再是人工智能提供可以计算的成套软件。现代代数算法结果的快捷性、直观性与准确性受到了私人的欢迎。例如，人们通过了解商品或服务的快速排名来选择自己的商品或服务，并以数据及其计算结果来评价各行各业的绩效。私法只有以一定的代数规范直面私人生活中的代数算法需求与普及，才能避免现实生活中各种代数算法对私人权益的损害。

四、完善与适用代数规范的建议

(一)完善私法制度中的代数规范

在成文法国家，法律规范是所有纠纷解决的根本依据，代数规范也是解决相应代数算法纠纷的法律依据。如果不存在代数算法黑箱，那么，民事判决活动中的大量算法瑕疵都是可能解决的。如果存在代数算法黑箱，即使法律适用技术再高明，也会因为缺乏算法的规范依据而出现各种算法瑕疵。可见，只要代数规范足够明确与全面，判决中的各种代数算法瑕疵均有望迎刃而解。

为此，私法必须完善其代数规范。这包括完善私法的计算单位规范、数量规范、计算公式规范、计算步骤规范、极值规范(最大值与最小值)等所有代数规范。这种完善不是一件容易的工作，其中有几点需要特别的强调：

第一，根据私人生活的变化来完善代数规范。早期私人生活所涉及的主要是债权债务的计算、违约金的计算、利息的计算等一些算术领域的问题，但是，随着经济社会的发展，出现了保险费率的计算、搜索引擎中的推荐算法与排名算法、证券化程序化交易程序等各种复杂算法。私法代数规范的完善应当既考虑对简单算法的调整，也考虑对复杂算法的调整。私法应当根据私人算法生活的发展而不断学习与调整新的算法，制定新的代数规范。当然，在调整传统领域的代数规范尚不完善的情况下，要同时完善新算法领域的代数规范，这是一件非常艰难的事情。然而，私法如果想为算法纠纷提供基本的算法规范，就不得不迎难而上。

第二，私法研究应当提高其代数水平，为完善代数规范准备数学基础。私法汲取了古典几何学的方法论，而未能及时引入代数算法，从而形成了私法与代数之间的巨大落差。今天，这一落差之大，足以使大量的私法学人望而却步。私法可以借口说，这种技术性问题应当由专家来解决而不是私法学人与法官来解决。初听之下，这种说法理直气壮。但是，私法要适应生活，而不是让生活来适应私法的无知。当我们从质与量的关系之上认识私法规范之时，会发现如果以此为借口，那么，私法规范的定量之维就因为这一借口而失去了存在与适用的可能。当今时代，没有哪门自然科学可以用不懂代数为由而将代数计算交给其他专家，私法学人有什么理由可以这样做呢？私法不得不学习代数算法，并将之运用于私法的立法与司法之中。长期疏离代数算法是私法的错误，而不应成为私法的借口。判决所面对的算法纠纷，使私法学人明确：我们必须学习代数算法并完善算法规范，以给出正确的判决结果与透明的计算过程。

第三，注意几何算法与代数算法的相辅相成。几何算法与代数算法是两种相辅相成的算法，建构概念与公理、演绎推理、构建逻辑图谱等几何算法固然重要，但代数算法也同样重要。私法不反对几何算法的公理与演绎，但是，私法也应重视代数算法，以达成二者相辅相成的关系。这就要求私法在其规范之中，既体现公理与演绎，也体现代数算法；在规范的总量与篇幅上，做到定性规范与代数规范大致均衡；在规范立法与适用之上，既重视演绎法，也重视四则运算、归纳法与概率论等各种代数算法。例如，合同法制度中的合同权利义务规范不应当局限于公理与演绎性界定，还应当包括数量与代数算法规则等。

第四，私法之中应大胆地运用代数表达方式。目前，私法规范与适用中少有阿拉伯数字、代数计算公式、代数符号等，而多运用文字表达代数规范。这既不简洁、不准确，也不便于代数运算。这种文字版表达在复杂的算法之中难以甚至无法进行计算。为此，私法规范应当大胆地引入代数表达方式，包括引入阿拉伯数字、代数计算公式、代数符号等。

第五，代数规范应作为私法制度的一部分而置于法律之中，而不要将代数规范作为司法解释甚至内部判决规则予以规定。目前，私法规范之中少有代数规范，但民事纠纷又需要代数算法，司法解释与判决规则于是成为代数算法规则的重要载体。证券法虚假陈述损失赔偿的算法、精神损失赔偿数额的算法、知识产权损失赔偿的算法、工伤事故损失赔偿的算法等，多规定于司法解释或法院内部的判决规则之中。这就形成了法律定性，而司法解释与判决规则定量的分工机制。这种分工机制轻视了代数规范，隐含着代数规范不如定性规范重要的观念。这种观念不符合定性与定量并重的基本原理，低估了代数规范的功能。私法应改变这种状态，将代数规范与定性规范置于同等重要的地位，在同一个法律文件之中同时规定定性规范与代数规范。

第六，私法还应注意算法实体规范与算法程序规范并重，即在诉讼法或仲裁程序中规定算法特别是代数算法的相应程序。例如，规定算法事实如何调查、算法主张如何质证与辩论、判决理由部分如何阐明不同的算法观点以及如何阐明与论证判决所确认的算法等。总之，应在程序法中加入算法程序，其中特别要注意研究与规定代数算法的独特程序。

(二)民事判决中重视代数规范的适用

私法通过正确地适用代数规范可以减少民事判决中的算法瑕疵，这要求在判决过程中根据具体的案情寻找适当的代数规范、进行充分的算法事实调查、根据算法程序进行算法陈述与辩论、阐述不同的算法观点及论证判决所确认的算法、对代数规范进行解释、根据所解释的算法得出计算结果等。在上述适用过程中，如下几点要特别予以说明：第一，根据算法程序进行充分的算法事实调查。从指导性案例看，这方面的调查存在明显的不足。根据当事人的争议，在庭审中应调查纠纷所涉及的数据、算法及其证据等；如果存在约定的算法，应对约定算法进行调查。庭审调查不能只调查定性方面的事实与证据，而必须调查算法相关的定量事实与证据。如果当事人对数据及其证据、计算公式等算法有不同的意见，应允许当事人对此进行质证与辩论，并将之记载于判决书之中。第二，在判决理由部分阐述不同的算法观点及判决所确认的算法。从指导性案例的判决书可以看到，一些算法显然存在不同的意见，但算法辩论、质证与论证在文书中少有表达。判决理由部分应评价当事人及其代理人提出的算法观点特别是不同的算法观点，对所采纳的观点与不予采纳的观点均应予以评论，并陈述理由。判决书不能忽视算法观点的论证，更不能忽视不同算法观点的记载与评论。第三，对代数规范进行解释。代数规范解释的重要对象是计算公式。一些代数规范本身已经包含了具体的计算公式，其解释相对简单。而另一些代数规范还没有形成明确的计算公式，这就需要通过法律解释来确立代数化的计算公式。代数规范的解释还包括对计算单位、参数、步骤等方面的解释，其一定要达到计算单位、公式与步骤等明确的地步，切忌只指出所涉及的参数而不管计算公式与步骤而进行估算的做法。第四，根据解释后的算法进行计算。这一计算过程应运用代数方式而不是文字表达方式，以达到简洁明确的效果。如果存在多个计算步骤，应分步骤逐一计算，以便于理解计算过程，不应直接给出计算结果而让当事人与判决书的读者揣摸计算步骤或结果的形成过程。第五，给出明确的计算结果。这包括明确的数量、量化的执行时间与量化的执行程序等。涉及到利息的，应当计算出利息数额，而不能仅仅指出利息计算方法。总之，算法事实、算法依据、计算过程、计算结果等均须明确，这样才达到了判决过程中的算法透明化。目前，代数规范的缺位使大量的算法无法可依，而只能以法院的内部规则甚至法官个人的算法经验予以填补，这给算法判决带来了不少困惑，也给上述算法的透明化带来了巨大的困难。因此，完善代数规范是上述算法判决透明化的基础，整个裁判过程既要重视定性裁判的透明化，也要重视定量裁判的透明化。

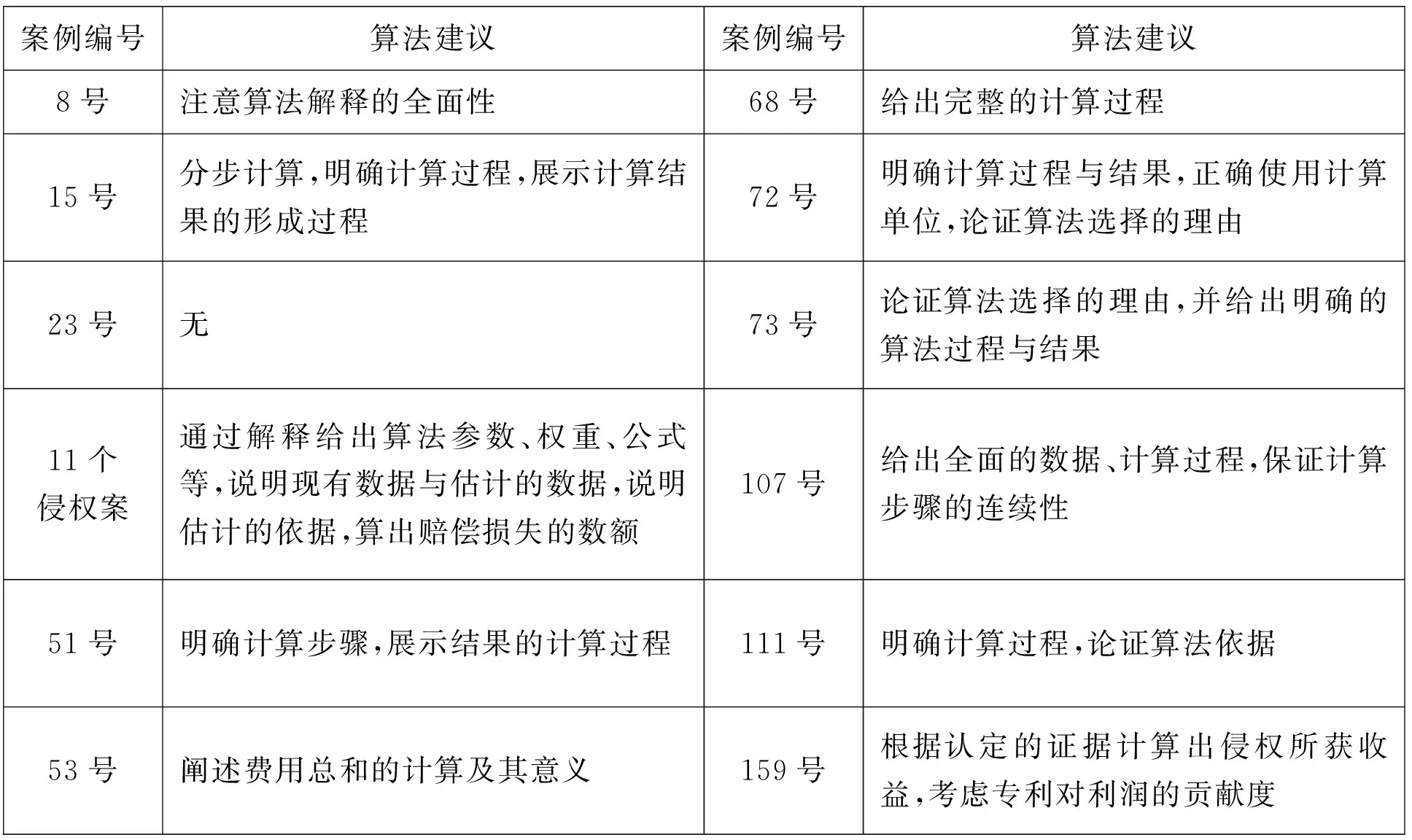
作为前文的回应，下面给出指导性案例中算法瑕疵的应对措施。需要说明的是，造成算法瑕疵的主要原因是代数算法黑箱，但对代数规范的完善需要更多的讨论，本文没有足够的篇幅完成，下表仅针对判决书原文中的算法瑕疵提出应急性的算法建议。

案例编号算法建议案例编号算法建议8号注意算法解释的全面性68号给出完整的计算过程15号分步计算,明确计算过程,展示计算结果的形成过程72号明确计算过程与结果,正确使用计算单位,论证算法选择的理由23号无73号论证算法选择的理由,并给出明确的算法过程与结果11个侵权案通过解释给出算法参数、权重、公式等,说明现有数据与估计的数据,说明估计的依据,算出赔偿损失的数额107号给出全面的数据、计算过程,保证计算步骤的连续性51号明确计算步骤,展示结果的计算过程111号明确计算过程,论证算法依据53号阐述费用总和的计算及其意义159号根据认定的证据计算出侵权所获收益,考虑专利对利润的贡献度

于此顺便建议，最高人民法院指导性案例不要局限于定性的判决理由的示范与指导，也应重视代数算法方面的示范与指导。因而，期望未来的指导性案例中有更多的代数规范适用与解释方面的案例。(60)这方面值得赞扬的是，在许某鑫等诉上海普天邮通科技股份有限公司证券虚假陈述责任纠纷案((2019)沪民终263号)中，上海金融法院运用了“多因子量化模型”等新算法取代了“普通加权平均法”等传统算法，更为精准地核定了证券虚假陈述导致的投资者损失。该案为2020年度上海金融法院十大典型案例之一。

(三)将算法规范作为人工智能中算法的指导

人工智能的发展使人们对算法黑箱充满了忧虑，这种忧虑多少有些忘记了法律规范的作用。在法治时代，任何算法均须遵守法律，人工智能中的算法也不例外。

算法规范应成为人工智能算法的准绳。法律应为算法纷争提供规则，算法规范就是这样的规则。尽管不少人工智能的算法领域还没有法律规范，但这不等于这些领域不应有法律规范。如果存在人工智能领域的算法规范，那么，适用算法规范解决算法纠纷就是了。在人工智能领域，私人的算法适用意思自治原则，但这并不意味着私法不调整该领域的算法，正如对其他私法领域的调整一样，私法应适度尊重私人的意思自治，但也要求人工智能算法遵守算法规范。例如，搜索引擎算法享有一定的自治空间，但这不等于其算法就不受到私法的调整，更不等于私法不应制定相应的算法规范。私法长期以来重视定性的调整，这导致代数规范的缺位，并形成了私法对人工智能算法无可奈何的印象。私法应当制定各种各样的算法规范特别是代数规范来调整人工智能千差万别的算法，为解决该领域算法纠纷提供法律规则。这要求私法在既有的法律之中加强算法规范的立法与适用，更要求私法加强人工智能领域算法的调整，建立相应的算法规范。

我们没有必要过度担忧机器深度学习会导致无法克服的算法黑箱问题。这种担忧忘记了一个不可忽略的事实：在法律领域，任何机器学习都不可能是无规则的学习，算法规范应成为机器学习以及其他任何法律人工智能程序的准则。无论机器学习的机制如何复杂，其中都蕴含着一个非常简单的道理：机器学习不过是模仿自然人的学习过程，比如，模仿自然人的神经网络学习过程。“通过机器学习生成的模型不可避免地反映了程序员的价值观、偏见。”(61)同前注，Emily Berman文，第1284页。在现代社会，任何自然人的学习均必须遵守法律与其他规则(如道德规则)，绝对不存在无规则的学习。夸大机器学习的无规则性，将机器学习作为法律之外的领域，这正如将网络空间当作另一个空间世界一样，既是不现实的，也是不合理的。法律承认人工智能的复杂性特别是机器学习的复杂性，但并不认同这种复杂性可以排斥法律规范特别是代数规范的调整；正如自然人自身的教育与学习一样，法律认同教育规律的复杂性与学习过程的复杂性，但从未将教育与学习置于法律调整之外。

在人工智能领域，私法要反对代数算法崇拜与代数算法不可控制的观点。在私法史中，代数算法受到了过度的轻视，与此形成鲜明对比的是，在人工智能领域，代数算法受到了过度的强调甚至崇拜，有时甚至被认为不可控制。对代数算法的过度轻视是不正确的，同样地，对它的崇拜也不可取。私法应认识到代数算法仅仅是一种定量的方法，它只有与定性方法相结合，才能全面而正确地理解与界定事物。在人工智能这一容易夸大定量方法的领域，尤其不应忘记定性方法的地位。几何算法中的公理法与演绎法，能将私法基本原则及其多层次的演绎性规范带入并贯彻于人工智能的算法之中。这可以保证人工智能的算法符合私法的特质，并为人工智能提供定性的控制。人工智能应当是定性方法与定量方法的结合，算法既必须受制于代数规范，又必须受制于定性规范。其中，代数规范为人工智能算法提供量上的控制，而定性规范为人工智能提供质的控制。人工智能必须遵守算法规范，它是可控制的，也是应当受到控制的。当代数算法发达时，认为数学是经验的，而当公理法发达时，又认为数学是演绎的。(62)参见梁芳：《数学机械化视野中算法与公理法的辩证统一》，载《中央民族大学学报》2014年第4期。这两种数学观念都不正确。私法应将定性方法与定量方法结合起来，将定性规范与代数规范结合起来，达到两种算法及其规范相辅相成的效果。

算法规范应当是相应算法的准则，我国法律人工智能也不例外。近年来，智慧法院之类的各种法律人工智能如雨后春笋般出现于公众的视野之中，但其算法却多不被知晓。无论其算法如何复杂，均应考虑到我国是成文法国家，法律人工智能均应遵守算法规范。以既有的判决书来反向推理判决的代数算法，这些反向推理肯定会对完善私法的代数规范有所帮助。只是这种反向推理违背了成文法国家法律适用的程序：它从判决结果推出判决规则而不是从法律规范演绎判决结果。更令人担忧的是，既有判决书本来就存在各种算法瑕疵，如果一些人工智能以此为据而回归或学习得出一定的算法规则，且再用于指导或预测新的判决，其结果可能与初衷背道而驰。如果真要建立私法领域的人工智能，那么，首先应完善私法的代数规范，其次是确立上述规范的解释规则，后面才是以此为据的人工智能系统的构建。以既有判决书为数据基础的人工智能系统构建，应坚持两点：第一，人工智能中代数算法的准则是代数规范，而不是判决书。判决书是代数规范适用的结果，而不是代数规范本身；从判决书中反向追索代数算法规则，是一个非常困难且不一定能得出正确结论的过程。第二，判决书可以作为代数规范的辅助，但必须是经过筛选的判决书。只有那些算法适当的判决书才能作为学习性资料而成为提炼算法的辅助性文件。但是，在习惯于定性判决而疏于代数算法的背景下，必须经过逐一论证才能确认上述文书中算法的合适性，其中检验过程是一个艰难的过程，如何完成尚需认真的讨论。

最后，私法不要因为人工智能而将简单算法复杂化。正如指导性案例所显示的那样，案件中的绝大多数算法均是算术即可解决的简单算法，而不是复杂算法。在商法特别是金融商法中肯定会遇到复杂算法，但那或许不是私法算法纠纷的常态。在私法中确立简单代数规范，在判决中认真适用简单代数规范，给出简单算法的计算过程，这既是大多数案件判决的要求，也是当务之急。解决这种燃眉之急，或许不需要复杂算法，也不一定需要人工智能。当然，人工智能的出现可以快速审理一些常见案件，可以减轻法院人少案多的压力，其发展对审判不无裨益。根据奥卡姆剃刀原则，人工智能的算法应当选择最简单的算法。(63)同前注②，[美]拉塞尔、诺文书，第519页。在法律人工智能领域，也应当恪守这一原则。