A design constraint for a double-acting telescopic hydraulic cylinder in a hydraulic erecting system
2022-02-17XiaolongZHANGJunhuiZHANGMinCHENGShenZHENGBingXUYuFANG
Xiao-long ZHANG ,Jun-hui ZHANG ,Min CHENG ,Shen ZHENG ,Bing XU ,Yu FANG
1State Key Laboratory of Fluid Power&Mechatronic Systems,Zhejiang University,Hangzhou 310027,China
2State Key Laboratory of Mechanical Transmissions,Chongqing University,Chongqing 400044,China
Abstract:Hydraulic erecting systems are widely used in missile and rocket launchers because of their high power density.The double-acting telescopic hydraulic cylinder(DATHC)plays a decisive role in the safe and proper operation of such systems.In particular,improper design of effective areas of a DATHC could potentially lead to an overspeed descent with severe damage for the erecting system.Unfortunately,there is no design constraint for DATHC to prevent this.Therefore,in this paper,a simplified and practical design constraint is proposed.Based on a developed mathematical model of a typical erecting system,we simulated and analyzed not only six cases meeting and not meeting the design constraint,but also the effectiveness of the design constraint under different loads.Experiments were then carried out under four cases.Simulation and experimental results validate the simplified design constraint,a constraint inequation guiding the design of diameters of effective areas for a DATHC.
Key words:Erecting system;Telescopic hydraulic cylinder;Overspeed descent;Design constraint
1 Introduction
Hydraulic erecting systems,which are used to raise or lower an erecting beam from one angle position to another,are widely used in missile vehicles,large construction machinery,and other mechanical devices(Yang et al.,2019).Due to the requirement for a long stroke in a limited mounting space,a telescopic hydraulic cylinder,also called a multistage hydraulic cylinder,is routinely adopted in such systems (Gao,2004).It is designed as a nested structure with gradu‐ally smaller diameters fitting within each other.The most prominent feature of a telescopic cylinder is its ability to provide an extremely long working stroke from a very compact retracted dimension.Telescopic cylinders can be divided into two types:single-acting and double-acting.Retraction of a single-acting tele‐scopic cylinder relies only on gravity or an external force when the pressure is released from the piston chamber.In contrast,a double-acting telescopic hy‐draulic cylinder (DATHC) with two oil supply ports is powered hydraulically in both directions.Accordingly,a DATHC is more complex in design.As a critical component of a hydraulic erecting system,there are multifaceted considerations for the design of a DATHC to ensure the reliability of the erecting system,such as strength,stability,and size of effective areas at all stages.
There have been many studies of the strength of a DATHC when it is fully extended.Prakash et al.(2020) proposed a method to determine the safe load of a two-stage pin-mounted hydraulic cylinder.The results obtained by this method were in good agreement with finite element simulation results.Uzny and Kutrowski(2019)investigated the influence of mount‐ing rigidity on the strength of a telescopic hydraulic cylinder based on the static stability criterion.Their results showed that the buckling capacity increased when the installation stiffness was increased.Wang et al.(2013) analyzed the stress and buckling behavior of a telescopic hydraulic prop under alignment load and eccentric load by finite element simulation.The results showed that a 360-type doubly-telescopic structure could withstand 1.1 times the eccentric load under the condition of full extension.Gupta et al.(2020)used the successive approximation method to determine the critical load of a two-stage hydraulic cylinder hinged at both ends,and the deviation was 3.63%.Li et al.(2015)put forward a dichotomous iterative method based on Python,through which the extreme load of a two-stage hoisting hydraulic cylinder can be quickly obtained.
To ensure the stability of a telescopic hydraulic cylinder during operation,Lgritskaia et al.(2021) ad‐opted two telescopic hydraulics with different installa‐tion angles to reduce the pressure impact during the switching stages in launch vehicles.Due to different installation angles,the switching times of the two tele‐scopic hydraulic cylinders were different:when one cylinder switched the stage,the other worked.In this way,the aim of reducing the pressure impact was achieved.Xie et al.(2014)established a mathematical model of a sizeable erecting system and designed a time-varying sliding mode controller whose perfor‐mance was better than proportion integration differen‐tiation (PID),according to the experimental results.However,the hydraulic actuator of this erecting system was not a DATHC.Several other papers have been de‐voted to the modeling and simulation of similar sys‐tems.Ritelli and Vacca(2013)developed a mathemat‐ical model of the counterbalance valve and analyzed the influence of its setting parameters on the energy consumption of a hydraulic crane system by a graphic method.Bak and Hansen(2013)optimized the opera‐tional reliability for an offshore material handling application,considering the instability of a pressure compensated directional control valve and a counter‐balance valve.Zhou et al.(2012)and Hou et al.(2017)proposed a simulation model of a hydraulic lifting system with a proportional directional valve,which was used to study whether a novel valve compensation strategy was effective.To simplify the model of a double variable load sensing system in an excavator,Lin et al.(2021)ignored the effect of the safety valve,check valve,and pipelines.Cheng et al.(2017)devel‐oped a mathematical model for a typical electrohydraulic system,which was used to investigate the dynamic characteristics of a proposed valve compen‐sation controller.
However,there have been few studies concerning the size of effective areas at all stages.If these areas are not properly designed,it will probably lead to overspeed descent,resulting in severe system damage and economic losses.Hence,there is an urgent need to develop a DATHC design constraint limiting its effective areas to prevent overspeed descent.Additionally,to avoid unexpected and destructive accidents,it is worth building a simulation model to prove the reliability of the design constraint before experimenting.Although the systems studied above were different from the erecting system,they provided references for the modeling in this paper.
To avoid overspeed descent and ensure the operational reliability of an erecting system,we derive a practical design constraint for a DATHC,which is effective even if there is a switch between overrunning load and passive load during operation.Then,a simulation model of a typical erecting system is established,by which preliminary verification of the effectiveness of the design constraint can be achieved.Subsequently,the experimental platform is described,and results of the verification experiment are given.Finally,the mechanism of the overspeed descent caused by failure to satisfy the design constraint is further discussed,based on the simulation results.
2 Design constraint of DATHC
2.1 DATHC description
A schematic view of a DATHC,a two-stage hydraulic cylinder,is shown in Fig.1.The first stage piston rod assembly (Stage 1),composed of piston 1 and piston rod 1,is nested in the barrel.Its piston chamber and piston rod chamber are represented by Chamber 1 and Chamber 2,respectively.Stage 1 is regarded as the cylinder tube of the second stage piston rod assembly(Stage 2)containing piston 2 and piston rod 2.Similarly,Chamber 3 and Chamber 4 respectively denote its piston chamber and piston rod chamber.Oil is able to flow between Chamber 1 andChamber 3 with pressurep
,whereas Chamber 2 and Chamber 4 with pressurep
are connected through a channel in piston rod 1.In Fig.1,d
,d
,d
,andd
are the corresponding diameters of the pistons and piston rods.When hydraulic oil is pumped into Chamber 1 and Chamber 3,Stage 1 extends with Stage 2.At the same time,the left end of Stage 2 is subjected to pushing force from Stage 1.Once Stage 1 is fully extended,the extension of Stage 2 relative to Stage 1 begins.With the movement of Stage 2,the oil in Chamber 4 is discharged to Chamber 2 via the internal channel in piston rod 1.As expected,the process of retraction is simply the reverse,and the port with pressurep
is the inlet in this case.2.2 Derivation of design constraint
An external force can change the state of motion of a body.Therefore,to ensure the DATHC extends or retracts without an overspeed descent fault,it is neces‐sary to carry out force analysis for Stage 1 and Stage 2.
According to the schematic diagram of forces acting on Stage 2 (Fig.2),the force-balance equation is given by:
whereF
is the external load of the DATHC andF
is the inertial force of Stage 2.The component force of gravity of Stage 2 is denoted byF
.S
andS
are the corresponding working areas of piston 2,andS
=f
denotes the friction force exerted on Stage 2 by Stage 1.F
is the force applied by Stage 1 on piston 2,which is generated by axial contact and extrusion between Stage 1 and piston 2.Accordingly,F
exists only if Stage 2 is fully extended or retracted relative to Stage 1.The forces acting on Stage 1 are shown in Fig.3.The force balance equation can be written as

S
andS
are the corresponding working areas of piston 1,f
is the friction force of the barrel against Stage 1.f′
andF′
are the reaction forces off
andF
,respectively.F
denotes the inertial force of Stage 1.The component force of gravity of Stage 1 is expressed byF
.F
is the force of the barrel against piston 1 due to axil extrusion.The combination of Eqs.(1) and (2) leads to the following equation:
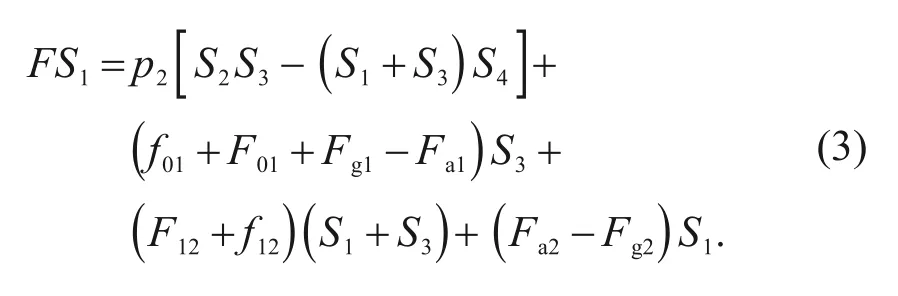
F
must exist and be greater than 0.In other words,hydraulic pressure alone cannot drive Stage 2 at this time.Moreover,F
=0 is true because there is no axial contact between Stage 1 and the barrel.As a result,from Eq.(3),the constraint on the normal operation of DATHC can be obtained as follows: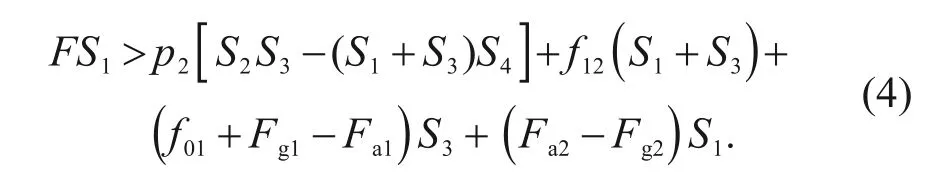
p
,F
,F
,F
,F
,f
,andf
are unknown until the design of the DATHC is completed,so inequation (4) cannot be used directly to determine the values ofS
,S
,S
,andS
in the design.Thus,it is necessary to simplify and modify the inequation to make it simple and easy to use.To accomplish this,some assumptions are proposed,as follows:(a) Since the mass of each stage of the DATHC is much less than the sum of the mass of the erecting beam and load,the influence ofF
andF
is not taken into account.(b) As the acceleration of each stage in the smooth operation of the erecting system is slight,the inertial force is ignored.
(c)In practice,the directions off
andf
change,but we merely consider an extreme case that is more likely to make inequation (4) untrue.That is,bothf
andf
are positive,andf
=f
=f
.It is assumed thatf
is very small and 2f
<p
S
is satisfied.The simplified inequation (4) can now be expressed as
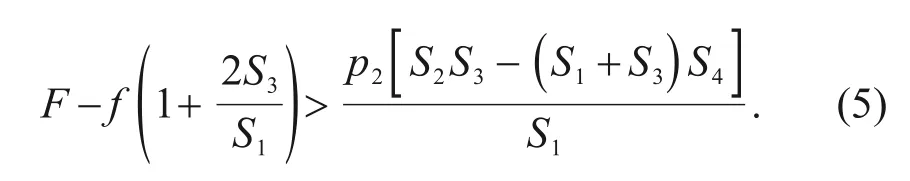
p
also can be substituted.SinceF
≥0 during the operation of the DATHC,we can conclude,according to Eq.(1)and the above hypotheses,that:
F
‒φ
relationship is shown in Fig.4.φ
is the angle between the erecting beam and the horizontal plane.G
is the gravitational force on the erecting beam and load.From pointC
toD
,F
is negative,which means that at least inequation (7) should be satisfied to make inequation(5)hold for anyF
.
Fig.4 Schematic diagram of F‒φ relationship

By substituting inequations (6) and (7) into inequation (5) and describing areas with diameters,a simplified and practical design constraint of a DATHC can be obtained:

λ
is the structural parameter of the DATHC,defined as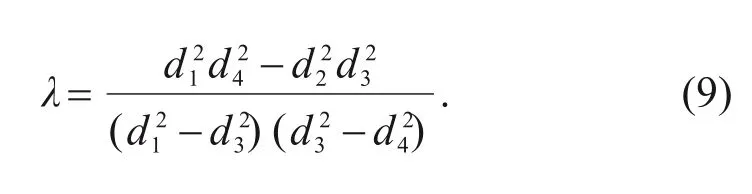
3 Modeling of hydraulic erecting system
A typical hydraulic erecting system is shown in Fig.5.In this section,a simulation model is established to evaluate the feasibility of the proposed design constraint.In this way,the damage caused by direct and rash experimentation can be avoided.To simplify the model,the following assumptions were made:
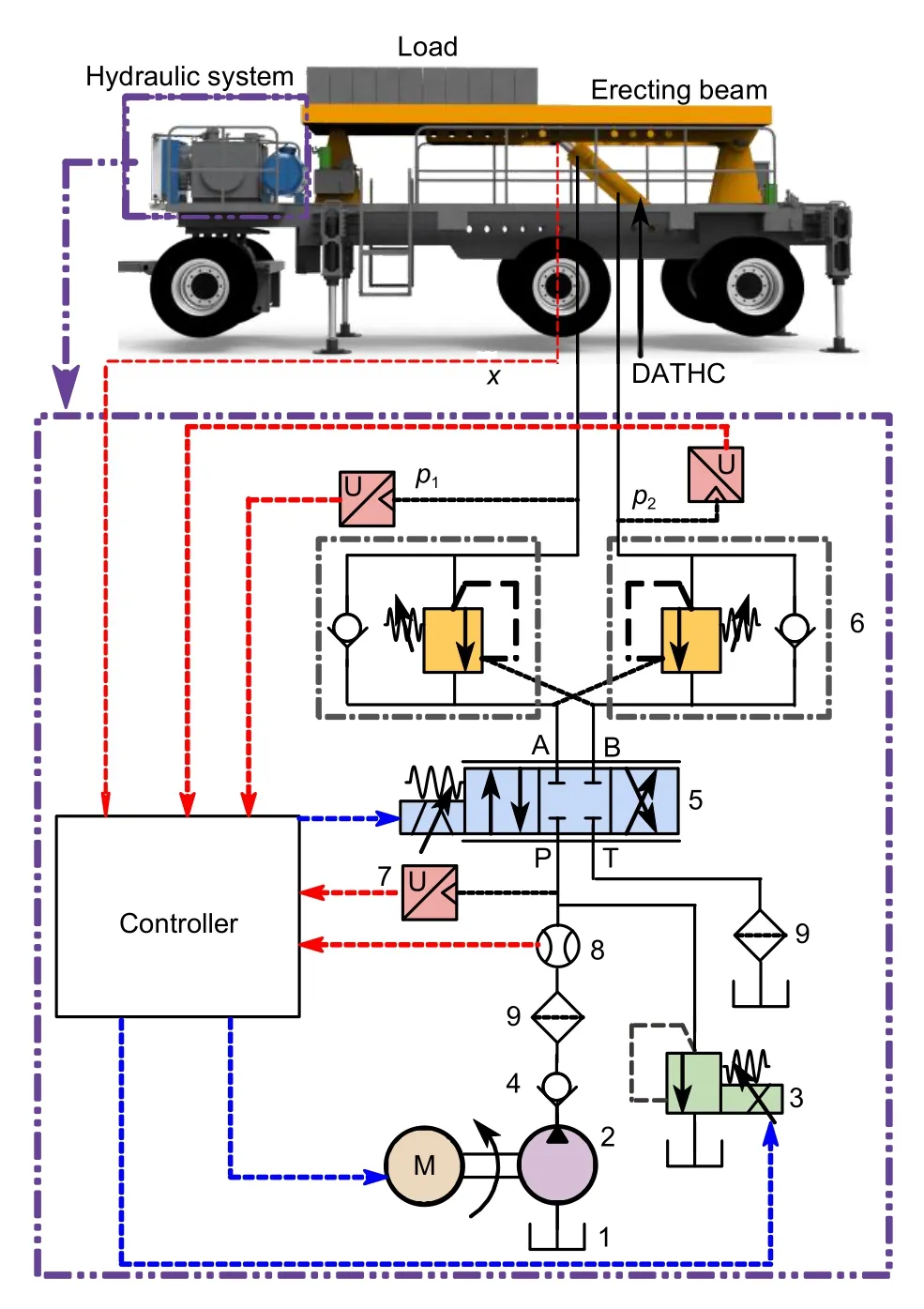
Fig.5 Hydraulic erecting system.1:oil tank;2:pump;3:pressure-relief valve (PRV);4:check valve;5:proportional directional control valve (PDCV);6:counterbalance valve;7:pressure sensor;8:flow sensor;9:filter. x is the displacement of the DATHC
(a) The influence of part compliance and fit clearance between them is ignored.Though they have a greater impact on system control accuracy,which is not the focus of this paper,they would have little influence on the research results of this study.
(b) At an operating pressure of 21 MPa,the deformation of the high-pressure hose(34.5 MPa)has little influence on the effective bulk modulus of the system,so it is ignored.
The leakage of the pump,which has a great influence on the flow rate of a hydraulic system,is considered,while the leakage of the valves is very limited by comparison and is ignored.
Given the effect of oil compressibility and leakage on the volumetric efficiency of the pump,the flow rate at the pump outlet can be expressed as(Park et al.,2020):

V
is the geometric displacement;n
is the speed of the pump;V
is the volume of the displacement chamber of the pump;β
is the effective bulk modulus of the hydraulic fluid;t
is the time;p
,Δp
,andc
respectively denote the operating pressure,pressure difference of the pump,and coefficient of leakage,which is calculated by substituting the actual measured pressure difference and flow rate,as well as the displacement and rotational speed in the pump manual,into Eq.(10).Ignoring the hysteretic behavior of the check valve,the flow rate across the check valve,whose flow rate-pressure drop characteristic is regarded as linear during the valve regulation,can be written as

p
=p
–p
–p
;p
is the pressure between the check valve and the PDCV;p
andk
represent the check valve cracking pressure and flow rate pressure gradient,respectively.Similarly,the flow rate of the PRV can be simplified and expressed as
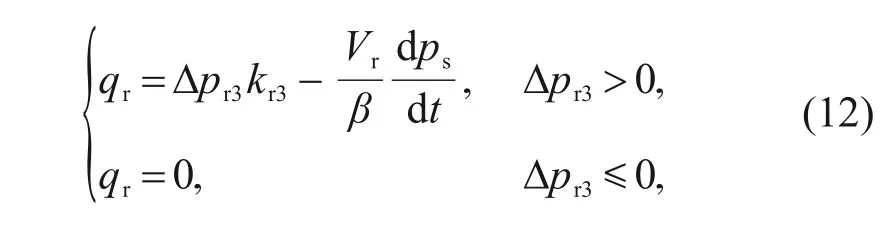
p
=p
–p
–p
;p
is the pressure of the oil tank;p
andk
are the PRV cracking pressure and flow rate pressure gradient,respectively;V
is the total volume of the connecting chamber between the check valve,PRV,and PDCV.The flow-pressure characteristic of the ideal PDCV is described by
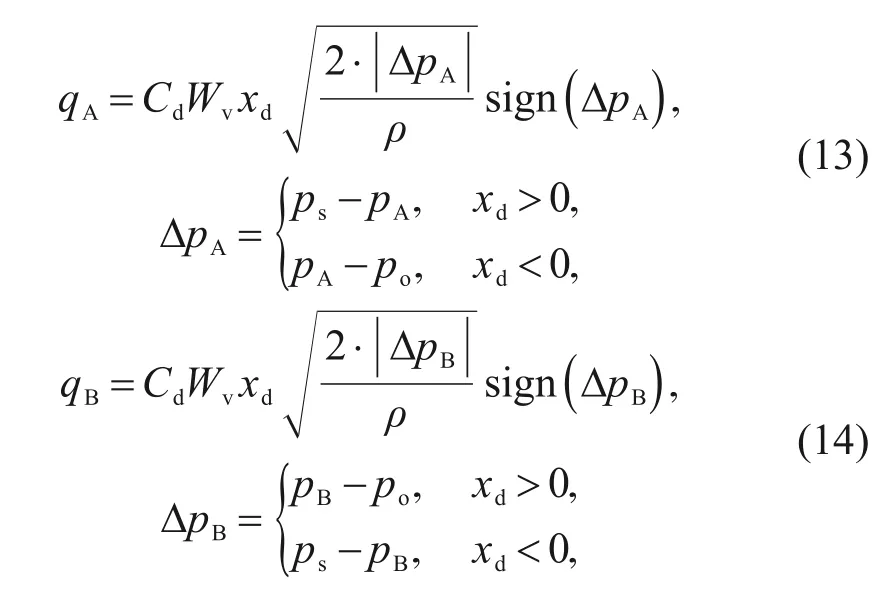
x
is the displacement of the spool,which is controlled by the input signal;q
andq
respectively denote flow rates in ports A and B,whose directions are determined by sign,a symbolic function;the pressures at ports A and B are indicated byp
andp
,respectively;C
is the flow coefficient;W
is the area gradient of the orifice;ρ
is the oil density.The counterbalance valve is composed of a main valve and a check valve.Consequently,the flow rate of the left counterbalance valveq
can be written as
q
andq
denote the flow rates through the main valve and check valve,given by:
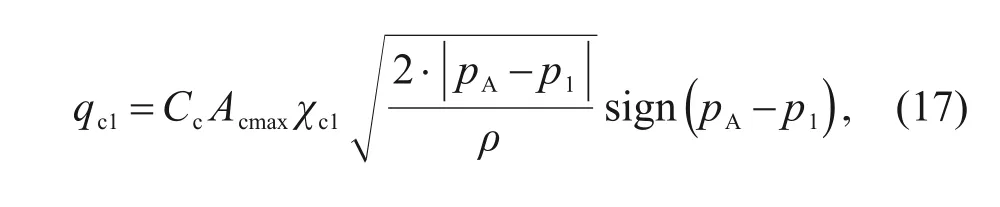
C
,A
,andχ
are the flow coefficient,maximum area,and fractional opening of the main valve,while the corresponding parameters of the check valve are represented byC
,A
,andχ
,respectively.χ
andχ
are calculated by:
κ
is the pilot ratio;p
andp
are the cracking pressures of the main valve and check valve,respectively;p
andp
are the pressures for maxi‐mum opening of the main valve and check valve,respectively.The relation betweenq
andq
is described as: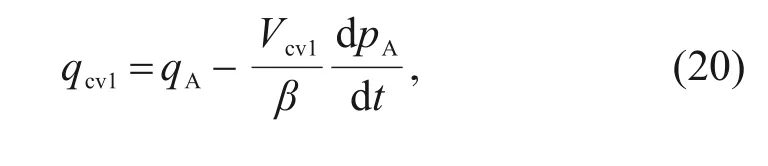
V
is the volume of the chamber between the left counterbalance valve and port A of the PDCV.The flow rate of the right counterbalance valveq
can be obtained following the same approach,and therefore is not shown here.For the DATHC,flow rates at port 1 and port 2 of the DATHC are expressed as:
V
denotes the volume of current Chamber 1 and Chamber 3;V
denotes the volume of current Chamber 2 and Chamber 4;V
is the sum of the dead volume and the volume of the chamber between the DATHC and the left counterbalance valve;V
is the sum of the dead volume and the volume of the chamber between the DATHC and the right counterbalance valve;x
andx
are the displacements of Stage 1 and Stage 2 relative to the barrel,respectively;x
andx
are the maximums ofx
andx
,respectively.The force balance equation of the DATHC was given in Section 2.1,as expressed in Eqs.(1)and(2).Nevertheless,there are some unknown variables that need to be further described.
Assuming that the stiction friction is equal to the Coulomb friction,and the Stribeck effect is not taken into account,one can obtain (Yanada and Sekikawa,2008;Tran et al.,2012):
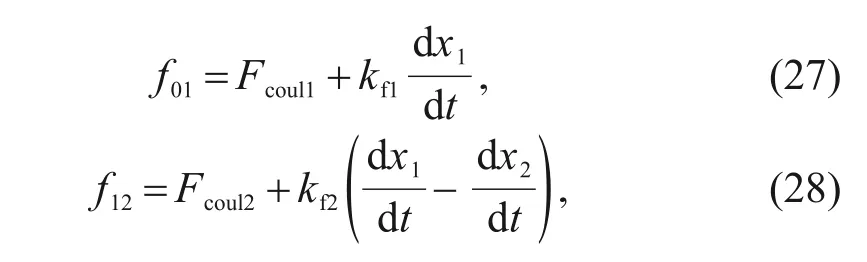
F
andF
are the Coulomb friction forces;k
andk
are the coefficients of viscous friction.F
andF
are calculated by a dissipative contact force model(Machado et al.,2012;Ylinen et al.,2014)that contains a linear spring and a linear damper,as follows: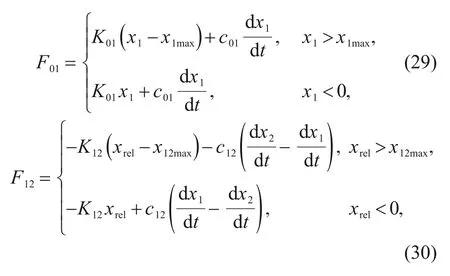
K
andK
are the contact stiffnesses;c
andc
denote the damping coefficients;x
is the maximum ofx
=x
−x
.Through the dynamic analysis of the erecting beam and the load shown in Fig.6,the expression of the external loadF
is derived (Wu et al.,2021) as follows: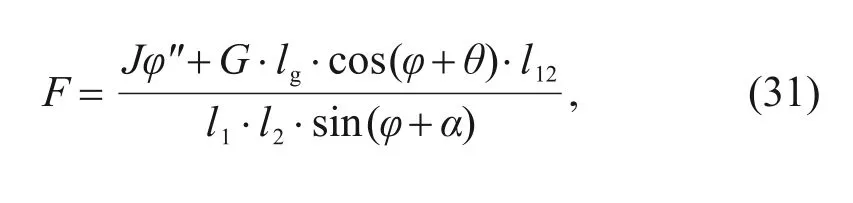
J
is the moment of inertia of both the erecting beam and the load;φ
″ is the angular acceleration.When the erecting beam is horizontal,the angle value of ∠o
oo
isα
,and the angle betweenoo
and the horizontal plane isθ
.l
,l
,l
,andl
are calculated by: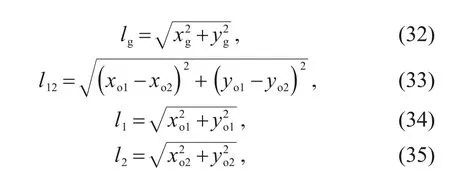
x
,y
,x
,y
,x
,andy
are indicated in Fig.6.Here,one absolute coordinate system (o
-x
y
) is defined whose origin (o
) is the hinge center between the erecting beam and bracket.Thex
-axis stays horizontal.x
andy
are coordinate values of the pointo
that is the hinge point at the barrel end of the DATHC.x
andy
are the coordinates of the hinge pointo
at the other end of the DATHC.x
andy
are the coordinates of the pointo
,the center of gravity of the load and the erecting beam.
Fig.6 Erecting beam and load
4 Results and discussion
4.1 Design constraint validation based on simulation
The simplified design constraint is an inequation involvingλ
in inequation (8).Therefore,first,the DATHC with differentλ
was simulated and verified.The crucial parameters of the system are shown in Table 1.4.1.1 Effectiveness at differentλ
In a horizontal state,the parameters of both the erecting beam and load,used to calculateF
,are as shown in Table 2.The external loadF
at this point is markedF
1.In this study,12 cases were simulated (Table 3).Note that the diameters conform to the China National Standard GB/T 2348 (SAMR,2018).Moreover,all control signals were consistent in each case.
From Table 3,the top six cases did not meet the design constraint due toλ
>−1.Their displacement curves are shown in Fig.7.The left region denotes that the control signal for PDCV is positive,which means that DATHC is controlled to extend.The right region denotes that the control signal for PDCV is negative.
Fig.7 Displacement curves of the DATHC in the first six cases
Table 1 Crucial parameters of the system
Table 2 Parameters of erecting beam and load for1
Table 3 Simulation cases with different
As expected,the speed was out of control in these six cases when the DATHC was retracted.Taking Case 1 as an example,we can obtain the velocity curve of the DATHC from Fig.8a.v
is the velocity of the DATHC.From 50 to 57.24 s (pointA
toB
),the retraction speed of the DATHC is always maintainedat 0.However,from 50 s the signal to control retraction is given,and the DATHC is supposed to retract.Then,from 60 to 70.55 s(pointC
toD
),its retraction speed varies from −0.021 to −0.024 m/s.Subsequently,the speed increases sharply,reaching −0.503 m/s at 74.69 s(pointE
).Following the accomplishment of switching stages at 76.56 s (pointF
),it is completely retracted at a speed of −0.026 m/s.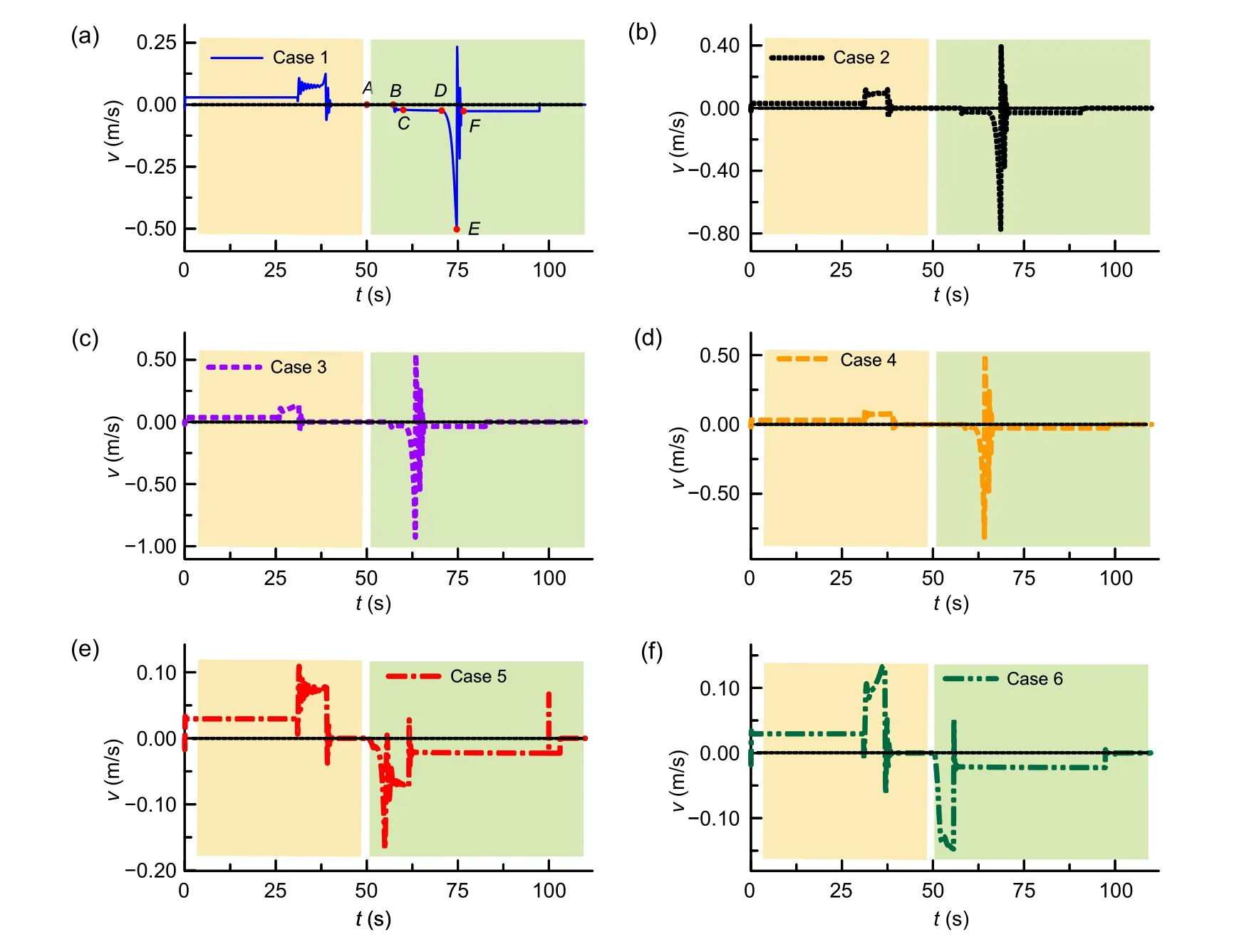
Fig.8 Velocity curves of the DATHC in Cases 1‒6(a‒f)
Case 6 had little effect on the displacement and velocity of the DATHC.This minor effect is difficult to observe from Figs.7 and 8f,but the displacement curve of Stage 1 in Fig.9 proves its existence.From 50 to 52 s,the displacement of Stage 1 changes slightly,but it is supposed to be standing still during this period.Because the value ofλ
in Case 6 is close to−1,the directions of the resultant forces on Stage 1 and Stage 2 easily change to correct directions.Moreover,the inertial forces and frictional forces are considered in the simulation,which are simplified or ignored in the derivation of design constraints.As a result,Case 6 had little effect on the performance of the DATHC.
Fig.9 Displacement curve of Stage 1 in Case 6
The simulation results of the remaining six cases are shown in Figs.10 and 11.Compared with Figs.7 and 8,it is evident that the DATHC in the last six cases is able to extend and retract successfully.According to Fig.11,from 50 s onwards,the DATHC begins to retract and a velocity step response occurs due to the step signal being inputted to the PDCV.
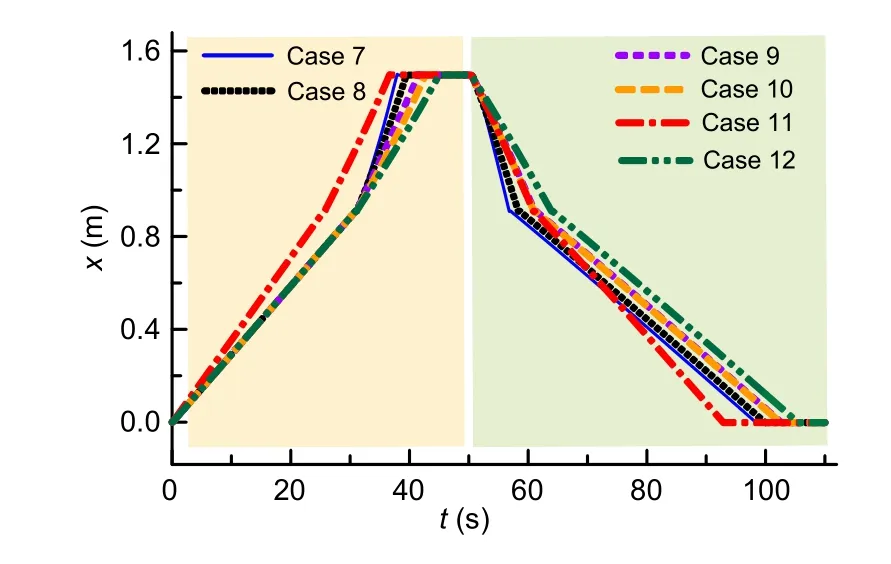
Fig.10 Displacement curves of the DATHC in Cases 7‒12
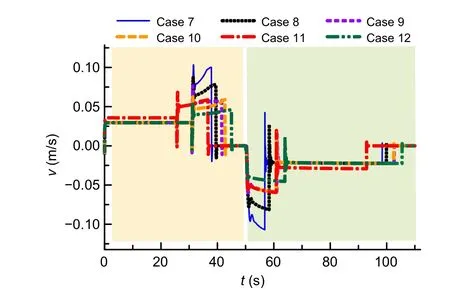
Fig.11 Velocity curves of the DATHC in Cases 7‒12
4.1.2 Effectiveness at differentF
valuesThe design constraint was proposed based on the DATHC force analysis,so it is necessary to conduct simulation and analysis on the DATHC under different values ofF
.According to Eq.(31) and in consideration of the follow-up experiments,differentF
values were obtained by changing the parameters in Table 4.It should be emphasized that the coordinate values in Table 4 are those of the erecting beam in the horizontal position.Then,multiple sets of simulations were carried out by applying the different loads in Table 3 to Cases 1–12 in Table 3.Taking Cases 3 and 8 as random examples,from Figs.12 and 13 we can see that the overspeeddescent fault of the DATHC in Case 3 emerges under different loads as shown by the positions of the circles in Fig.12,while that of Case 8 does not.Similar conclusions can be drawn from the rest of the cases.Therefore,the design constraint is still valid for different values ofF
.Table 4 Different parameters for different
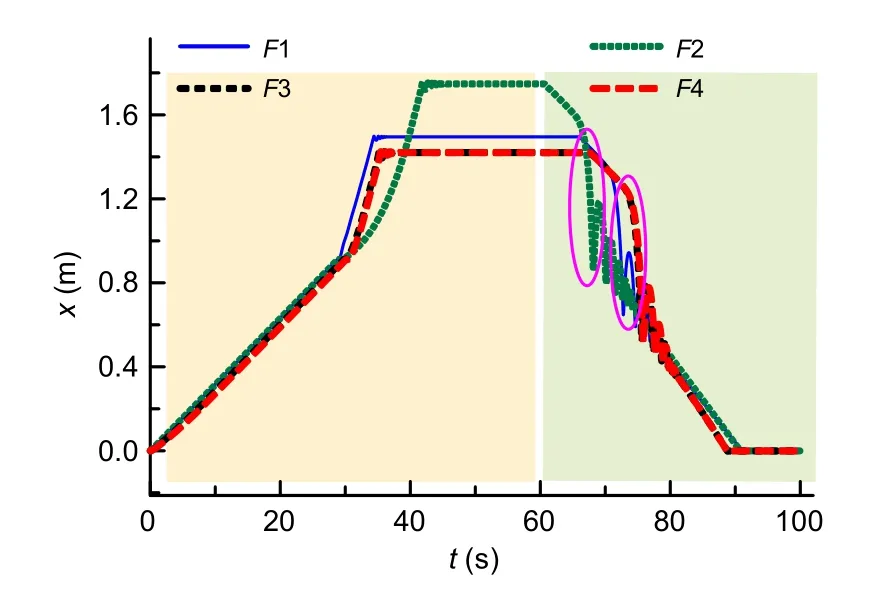
Fig.12 Displacement curves of the DATHC in Case 3 with different loads

Fig.13 Displacement curves of the DATHC in Case 8 with different loads
4.2 Design constraint validation based on experiments
4.2.1 Experimental platform
To further verify the effectiveness of the design constraint,an erecting system experimental platform was built(Fig.14).A schematic diagram of its hydraulic system is shown in Fig.5.A displacement sensor was mounted on the DATHC to measure the displacement characteristics.The two ports of the DATHC and the“P” port of the PDCV were each equipped with a pressure sensor to obtain their dynamic pressure.A flow sensor was used to monitor the flow rate of the hydraulic pump to the DATHC.There are two ways to change the force acting on a DATHC.One is to change the number and installation positions of the load blocks installed on the erecting beam.The other is to adjust the position of the two hinged joints of the DATHC.In this way,the test rig was able to apply different loading forces on the DATHC (Table 4) to test the effectiveness of the design constraint under differentF
values.
Fig.14 Photo of the experimental platform
4.2.2 Experimental results
Because of the high manufacturing cost of the DATHC,only two cases were tested:one that met and one that did not meet the design constraint.As with the selection in Section 4.2.1,the two DATHCs were processed according to the parameters in Cases 3 and 8.Considering the damage caused by a possible drop for Case 3 not meeting the design constraint,Case 8 satisfying the design constraint was first tested under the heavy loadsF
2,F
3,andF
4(Table 4).Case 3 was subsequently tested under the light loadF
1 (Table 4).Moreover,for the sake of reducing the swing of the erecting beam caused by pressure impact and collision during the experiments,the DATHC was slowed down in advance when it reached the switching stage position of the DATHC and the 90°position.This was done because the swing of the erecting beam could cause a greater inertia force due to the large moment of inertia which could affect the stability and safety of the experimental platform.In addition,the measured displacement signals were simply filtered for the convenience of subsequent comparison and analysis.The filtered displacement signals of the DATHC are shown in Figs.15 and 16.
Fig.15 Experimental displacement curves of the DATHC in Case 8
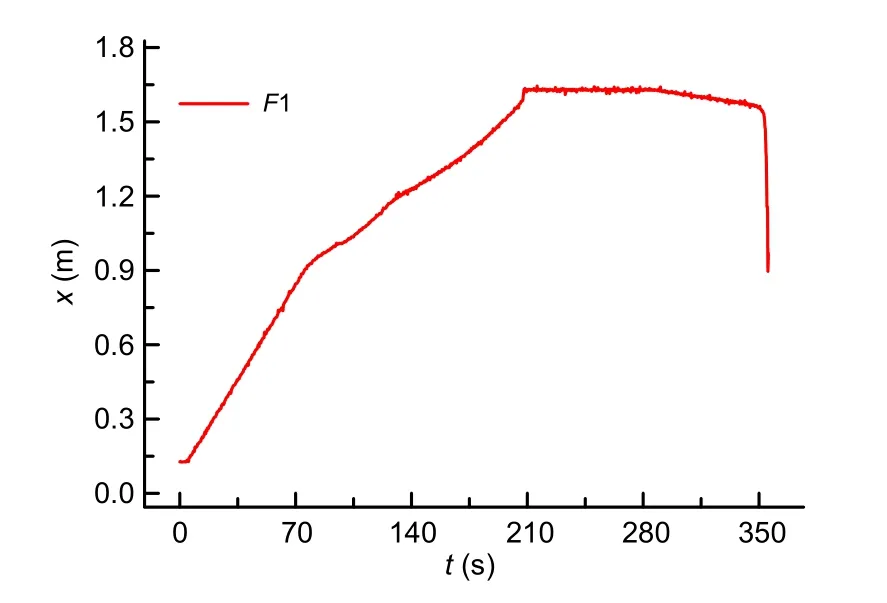
Fig.16 Experimental displacement curve of the DATHC in Case 3
As is evident from Figs.15 and 16,Case 8 still worked properly with different loads,whereas Case 3 experienced overspeed descent from 353.25 to 355.65 s,during which time the DATHC retracted 0.594 mm.These data indicate that the overspeed descent causes a rapid retraction only in Stage 2,which is consistent with the simulation results.After the occurrence of this fault,the experiment was terminated to avoid potential security hazards.
4.3 Further discussion
The above simulation and experimental results show that an overspeed descent fault of the erecting system will occur when the DATHC does not meet the design constraint.However,the mechanism of this fault is worth considering.
UsingF
1 in Case 3 as an example,the simulation displacement curves of Stage 1 and Stage 2 are shown in Fig.17.A schematic diagram of the overspeed descent process is shown in Fig.18.The blue arrows indicate the direction of movement.
Fig.17 Displacement curves of Stages 1 and 2 in Case 3

Fig.18 Evolution of the fault of overspeed descent.(a)‒(d)indicate the states of DATHC corresponding to (a)–(d) in Fig.17.References to color refer to the online version of this figure
Firstly,because the diameters of the DATHC in Case 3 do not satisfy the design constraint,inequation(4)does not hold at the 90°position.According to the force analysis in Section 2.2,Stage 1 first retracts by resultant force,which corresponds to(a)‒(b)in Figs.17 and 18.During this period,the erecting beam does not rotate due to the static Stage 2.
Then,after Stage 1 retracts a certain distance,Stage 2 is pulled by Stage 1 and retracts in synchrony,as seen in Figs.17 and 18 from(b)to(c).As the pulled Stage 2 retracts,the erecting beam is continuously lowered.At the same time,owing to the changing moment arm of the gravityG
,the external loadF
acting on the DATHC gradually increases,varying from a pulling force (negative) to a pushing force(positive).At some instant,the underlying inequation (4)starts to be true with increasing values ofF
,which means that the direction of the net force on Stage 1 changes.As a result,Stage 1 is required to extend to the maximum stroke position,as indicated in Figs.17 and 18 from(c)to(d).With the extension of Stage 1,the volume of Chamber 1 increases,which causes oil in Chamber 3 to be sucked into Chamber 1,while oil from Chamber 2 is squeezed into Chamber 4.This process will accelerate the retraction of Stage 2,and in turn,the retraction of Stage 2 will promote the extension of Stage 1.Because of this positive feedback loop,Stage 1 extends rapidly and Stage 2 quickly retracts,which leads to the overspeed descent of the erecting beam.If the diameters of the DATHC meet the design constraint,then the underlying inequation(4)is always satisfied,and the above fault will not occur.
5 Conclusions
In this study,to avoid the overspeed descent fault of an erecting system caused by the improper design of a DATHC,a simplified design constraint was derived.After simplification,the design constraint related only to the diameters of the four effective areas of the DATHC,which makes the constraint easier to use for the design of DATHC.Then,multiple sets of simulations and experiments were performed to verify its effectiveness.The results showed that if the structural parameter of the DATHC,defined in Eq.(9),is less than −1,the erecting system will not have an overspeed descent fault.Moreover,the effectiveness was verified under different external loads.We also conclude that the design constraint is applicable not only when the DATHC is pushed and pulled during operation,but also when on‐ly a pushing or pulling force is applied to the DATHC.
When the design constraint is not satisfied,with increasing load force,the direction of the resultant force on Stage 1 changes during the retraction,then Stage 1 begins to extend while Stage 2 retracts.Since the two movements promote each other,the rate of descent goes out of control.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (No.91748210) and the National Out‐standing Youth Science Foundation of China(No.51922093).
Author contributions
Xiao-long ZHANG designed the research.Xiao-long ZHANG and Jun-hui ZHANG wrote the first draft of the manuscript.Shen ZHENG set up the test rig and processed the experiment data.Min CHENG helped organize the manuscript.Bing XU and Yu FANG revised and edited the final version.
Conflict of interest
Xiao-long ZHANG,Jun-hui ZHANG,Min CHENG,Shen ZHENG,Bing XU,and Yu FANG declare that they have no conflict of interest.
