顾及物方坐标误差的张正友标定算法

瞿 锴,郭中佑,唐育林,陈抒录,陈朋明

(1.中机国际工程设计研究院有限责任公司,长沙 410021;2.湘潭大学 土木工程学院，湖南 湘潭 411100;3.湘潭市勘测设计院，湖南 湘潭 411100)

0 前 言

近年来，无人机摄影测量技术得到了迅猛发展，在生产实践中广泛应用于农业、林业、海洋等领域[1]。在无人机摄影测量中普遍采用非量测型数码相机，但其存在着相机光学畸变大的缺点，故需要对相机成像参数予以检校。相机检校是通过对已知坐标或相对位置关系明确的物体进行拍照，利用物体相片量测坐标与已知坐标之间的对应关系来求取相机成像参数。为保证参数解算的可靠性，通常需要进行大量的多余观测，这些数据被认为服从高斯-马尔可夫模型(Gauss-Markov Theory)，可构建众多的观测数据方程，在最小二乘准则约束下求解方程获得参数的最优估值。相机检校常用的Tsai算法、张正友标定算法、灭点法和直接线性变换(Direct Line transform，DLT)算法在计算相机参数时都采用了G-M模型[2]。但G-M模型只考虑了观测向量包含误差，则将导致应用传统最小二乘准则估计的参数不是最优解。

考虑到G-M模型的缺点，整体最小二乘准则被提出并逐渐应用到上所述相机检校工作中所列方程求解的约束条件[3]。如陶叶青[4]、杨会军[5]、孔建[6]、鲁铁定[7]和孙培芪等[8]将整体最小二乘应用到解决方案中去，实验结果表明，整体最小二乘在拟合函数、转换参数的求解问题中更加具备优势。其次是检校场类型对相机检校起着很重要的作用，倪静、曹良忠等[9-10]研究了相对条件较为苛刻的野外检校场、田雷等[11]应用了室内检校场检校、李平[12]简化了三维空间检校场，应用二维检校场进行相机检校中比较出名的是张正友检校法[13]，这种方法只需要一个规则的格网状平板，通过移动相机从不同位置对其拍照，即可计算出内外方位元素。

考虑到野外检校场和室内三维检校场建立与维护的不易，而无人机摄影测量相机又需要频繁检校，本文采用自制的格网型模板，先以尼康D800为例，利用控制变量法分析相片数量和拍摄角度对参数解算精度的影响，确定相片数量和拍摄方式后，使用Nikon D800相机与索尼ILCE-7R相机拍摄模板获取数据。接着，考虑到整体最小二乘算法较最小二乘算法的模型更为完善，顾及到了模型中系数矩阵可能存在的误差，使用整体最小二乘算法对张正友检校算法予以改进，并通过试验进行验证，以提高非量测相机的检校精度，保证测绘生产获得较高质量的成果。

1 研究方法

自检校方法是Maybank[14]提出的一种与相机移动和空间几何信息无关的相机检校方法。这方面国内的工作有孟晓桥等[15]从多个方向拍摄模板图像，应用圆检校算法，利用射影的不变性，解算出了相机参数。从计算原理讲，张正友检校法也可以归于自检校方法。相机的自检校方法是指不需要依据一个已经建立好的检校场，是通过影像与影像之间的对应关系，计算出相机的参数。此种方法的优点是价格低廉，可以随时随地对相机进行检校；缺点则是精度会比较低。张正友相机标定算法是将打印的棋盘格贴在平面上，从不同角度进行拍摄，利用像点和物点的几何关系确定相机内外方位元素的初值，然后将其作为非线性相机几何模型的初值，求出单应性矩阵，以此解算出摄像机内外参数和畸变系数，模型如图1所示。

图1 张正友算法模型

1.1 单应性矩阵

设世界坐标某点的物理坐标为M=[U,V,W,1]T，其对应的像素坐标系下的像素坐标点为m=[u,v,1]T，故标定用的棋盘格平面到图像平面的单应性关系为：

(1)

其中:s为尺度因子;A为相机内参矩阵;包括仿射变换和透视投影;(u0,v0)为像主点坐标;α,β为焦距与像素横纵比的融合;γ为径向畸变参数;R为旋转矩阵;t为平移向量;[Rt]也被成为相机的外参矩阵。

设棋盘格平面W=0，可得：

(2)

A[r1,r2,t]为单应性矩阵，即内参矩阵和外参矩阵的积，记作H=[r1,r2,t]，得：

(3)

所以每一格标定板的角点可以提供两个坐标约束方程：

(4)

上式对于同一张图片上所有的角点均成立，其中[u,v]是像素坐标系下标定板的角点坐标，[U,V]是世界坐标系下标定板的角点坐标。

1.2 内参矩阵A和外参矩阵的计算

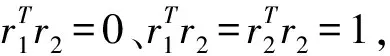
(5)

化简得：

(6)

公式(6)中：v是仅包含H元素的矩阵，b=[B11,B12,B22,B23,B33]T。由于矩阵H已知，矩阵v又全部由矩阵H的元素构成，因此矩阵v已知。每张标定板图片可以提供一个约束关系，采用最小二乘拟合最佳的向量b，得到矩阵B，所以有：

(7)

相机的内参矩阵A取决于相机的内部参数，无论标定板和相机的位置关系怎么变换，相机的内参矩阵是不变的。而外参矩阵反映的是标定板和相机的位置关系，对于被拍摄的不同图片，标定板和相机的位置关系已经改变，此时每一张图片对应的外参矩阵都是不相等的。

因为H=A[r1,r2,t]，求解得到H和A后，可通过式(8)得到外参矩阵。

[r1,r2,t]=A-1H

(8)

1.3 畸变系数k的计算

对于畸变系数k，张氏标定法只关注了影响最大的径向畸变，数学表达式为[18]：

(9)

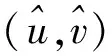
k=[k1,k2]T=(DTD)-1DTd

(10)

1.4 整体最小二乘原理

在实际工作中，系数矩阵中也会包含误差[7-8]，故真误差的数学期望往往不为0。求解Ax=b时，应该同时考虑C和c二者的误差和扰动，令B矩阵的误差扰动为E，向量b的误差向量为e，矩阵方程为：

(C+E)x=c+e

(11)

可得：

c+e-(xT×I)E-Cx=0

(12)

式中:xT×I表示两个矩阵做克罗内克积，令F=[i,-(xT×I)],v=[e,E]T，可得：

Fv+c-Cx=0

(13)

整体最小二乘准则为：

minφ=vTPv-2λT(Fv+c-Cx)

(14)

式中:P为权矩阵;λ为Largrange乘数，分别进行偏导：

(15)

可得：

x=[(C+I)T(FP-1F)-1C]-1(C+I)T(FP-1F)-1c

(16)

对公式(6)和公式(10)采用整体最小二乘计算，得到最优估计值。

2 检校场与计算软件的设计

2.1 室内二维检校场的实现

这里选用尼康D800和索尼ILCE-7R两种相机获取影像数据，拍摄时设置为手动曝光方式，物镜对焦于无穷远，相机传感器参数见表1。

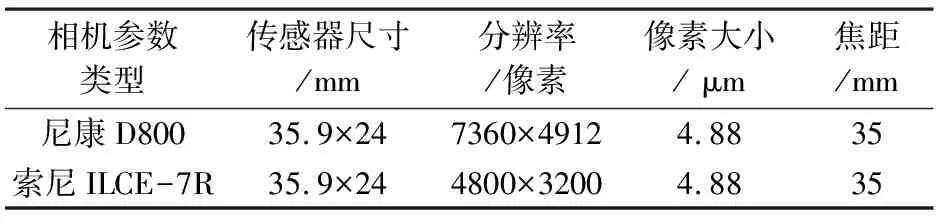
表1 尼康D800和索尼ILCE-7R相机传感器参数

计算机型号为联想Lenovo G50-70 20351笔记本电脑，CPU酷睿i5-4258U，内存DDR3L 1600 MHz。实验选取棋盘格作为相机检校的模板，二维控制场采用基于纯平液晶显示器的检校方法[19]，使所有控制点在一个平面上。

为研究拍摄角度对标定精度的影响，从不同角度进行拍摄，得到图像，棋盘格大小为9×5个方格，每个方格尺寸为45 mm × 45 mm(长×宽)，角点数量为32个，部分影像如图2所示。

图2 不同方向拍摄的棋盘格控制场

2.2 相机检校软件的设计

这里根据计算原理利用Visual Studio平台和C#设计相机检校软件，主要分为如下几项功能：文件读取数据、最小二乘约束、整体最小二乘约束、畸变改正、查看报告和退出等功能。程序操作非常简便，首先点击可执行文件(.exe)，启动相机检校程序，在相同目录下添加不同角度拍摄的棋盘格影像，可以为tif、jpg、bmp等格式，使用对应算法自动提取棋盘格角点的坐标作为后续计算的数据，程序解算会自动将最小二乘约束与整体最小二乘约束解算所得到的参数值作为初始值使用，直接点击计算输出按钮可得到最终的相机参数报告，包括最小二乘约束下和整体最小二乘约束下的不同相机检校算法的相机参数。参数解算部分结果如图3所示。前面部分为相机的检校参数值，后面部分为各参数的解算误差。

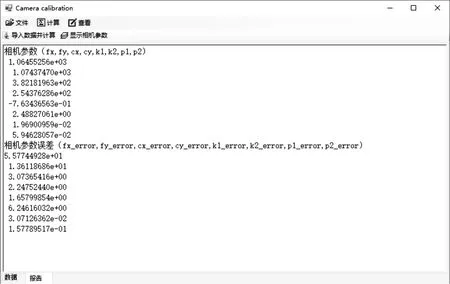
图3 相机检校软件

3 实验结果与分析

3.1 相片数量对检校的影响

为探究相片数量对相机检校精度的影响，依次使用3、5、7、9、11不同数量的相片参与计算，结果如表2所示，参与解算相片数量的不同会导致检校参数的精度有所差异。相机参数包括：f(焦距)，x0、y0(主点坐标)和k1、k2(畸变参数)。y值在3张相片解算时最优，后面呈波动分布。f值在9张相片解算时达到最优，11张相片为35.85445，相比而言，值下降了0.066。x0、k1和k2的值随着参加解算相片的数量越多，精度越高，分别为3661.5、-0.0114和0.0403。3张相片进行解算时，f、k1和k2与参考值相差最大，这是因为相片的数量太少导致不能够充分反应出镜头的畸变情况。随着后面参与解算的相片数量越来越多，值变化的越来越趋于平稳状态，说明相片并不是越多越好，但也不能太少，过少会使得结果精度不高，过多则会导致计算量的增加，从而导致效率降低。

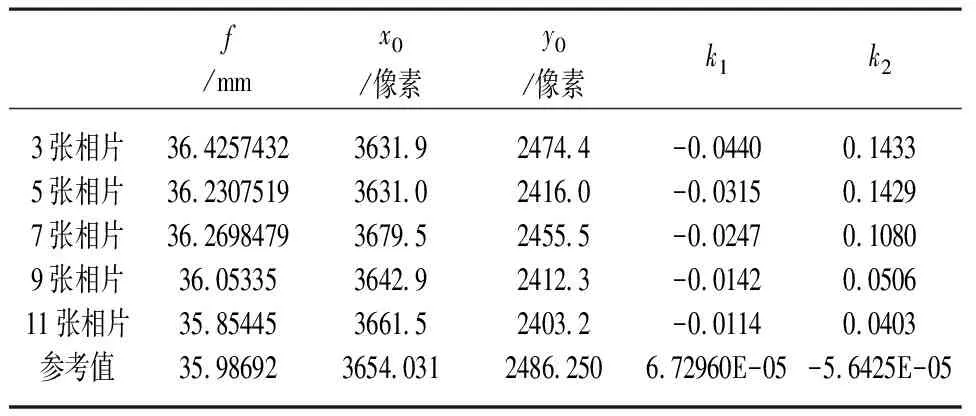
表2 尼康D800相片数量与检校参数计算结果

3.2 拍摄角度对检校的影响

为探究拍摄相片的角度对检校结果的影响，采用两种方式拍摄相片，先拍摄一组近似平行的照片计算检校参数，再以不同的角度拍摄相片计算检校参数，分析得到的检校结果，两组相片的检校结果如表3所示。当相机位置处于平行状态时，f和x0的精度较高，分别为35.96734和3654.2；相片处于不同的角度时，y0、k1和k2精度较高，依次为2404.7、-0.006、0.019。一般认为，近似平行的相片计算的检校参数精度会低于不同角度拍摄的照片计算的检校参数精度。因为张正友检校方法是通过不同相片之间的关系计算的，所以拍摄的相片近似平行的时候，有的参数之间会存在很强的相关性，就会影响最后的结果。在使用张正友标定法对相机进行检校时，应该以不同的角度对棋盘格进行拍摄，从而保证高精度的校验结果。y0、k1和k2的精度与预期表现相符，而f和x0的结果精度恰恰相反，可能与相片拍摄的质量有关。

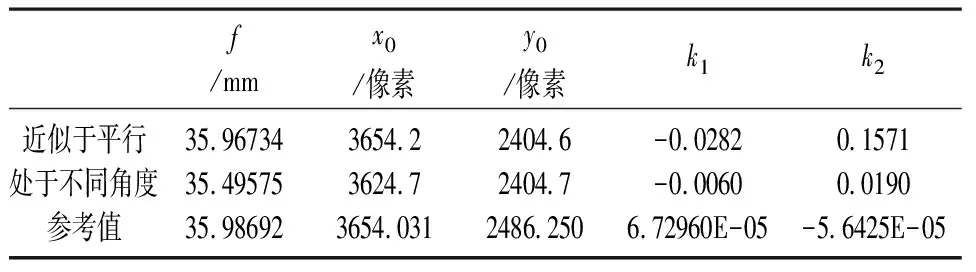
表3 尼康D800相机拍摄角度与检校参数计算结果

3.3 改进前后方法的对比

由以上可知，相机拍摄相片时应尽量从不同方向进行拍摄，数量根据区域大小确定，本次使用11张不同方向拍摄的相片参与解算。为检验改进前后张正友方法在尼康D800和索尼ILCE-7R两种相机中的情况，分别使用两款相机随机在5个摄站对棋盘格进行拍摄，每张相片不重复，角点数量为45个，部分图片如图2所示。分别采用经典最小二乘算法与整体最小二乘算法求解单应性矩阵参数，进而解算相机参数，并将结果进行对比分析。表4为尼康D800和索尼ILCE-7R相机内定向参数计算结果，在尼康D800数据集上，LS和TLS法得到的焦距f与参考值分别相差0.421 mm、0.259 mm；主点坐标(x0，y0)分别相差176.117像素、44.159像素；畸变参数k1/k2分别相差0.037/0.012、0.466/0.150；计算时间相差0.345。在索尼ILCE-7R数据集上，LS和TLS法得到的焦距f与参考值分别相差0.435 mm、0.120 mm；主点坐标(x0，y0)分别相差155.731像素、93.362像素；k1/k2分别相差0.1225/0.110、0.150/0.128；计算时间相差0.185。相比LS，TLS计算得到的参数精度均得到了不同程度的提升，说明TLS确实能够较好的考虑观测值和系数存在的误差，解算出更为精确的结果。虽然相机参数精度均有提升，但增加了计算时间，这是必然的结果，因为计算量的增加，势必会导致计算效率的降低。总的来说，整体最小二乘方法相比传统的最小二乘方法在张正友标定算法相机参数解算中表现更优。

4 结 论

本文在传统张正友的算法上进行改进，考虑顾及物方控制点坐标误差，用整体最小二乘约束求解单应性矩阵，将其精度得到提高的结果参与后面相机参数的运算。为确定最佳解算相片数据，先以尼康D800为例，使用控制变量法探究拍摄角度和相片数量对解算结果的影像。然后采用改进前后的张正友标定算法在尼康D800和索尼ILCE-7R相机开展实验，结果表明：

(1)解算参数x0、k1和k2的值随着参加解算相片的数量越多，精度越高，值逐渐趋于平稳，说明盲目增加相片数量不会一直提高解算精度，反而会增大计算量。

(2)以不同角度拍摄的照片计算的检校参数y0、k1和k2精度高于近似平行的相片计算的检校参数精度，不同角度的相片能够更好提供约束条件，得到更优解。

(3)在尼康D800和索尼ILCE-7R数据上，相比传统张正友算法，f(焦距)、x0、y0(主点坐标)和k1、k2(畸变参数)的解算精度均得到了提升，但计算量提升了一倍，这在预期之内。

本次实验的某些相机参数精度与预期不相符，可能是因为相片质量没有做抗差估计，在进行解算时无法保证每张相片的质量统一，从而导致结果出现差异性。后面可以针对不同相机检校算法验证本文所提方法的可行性，并为了保证数据质量统一标准，对拍摄相片进行抗差处理。