数据融合中基于聚类的成员系统选择算法*
2022-02-16张振张芳
张 振 张 芳
(江苏大学计算机科学与通信工程学院 镇江 212013)
1 引言
随着信息技术的发展,大量的信息内容推动了信息检索系统[1]的开发,由于检索系统中检索模型[2]存在差异,因此生成的结果列表也有差异。数据融合的出现很好地解决了进一步提升检索结果的问题,在略读效应[3]、合唱效应[4]的作用下整合多个检索结果列表以增强检索性能。研究表明[5]参与融合成员系统的增加,有利于融合性能的提升。但成员系统过多时,融合过程的时间复杂度增加,冗余和质量差的成员系统影响[6]影响了融合效果进一步提升。因此,如何在大规模成员系统中选择一组合适的成员系统参与融合并使最终的融合性能明显提升,是一项具有挑战性的任务。Antonio[7~8]等提出了一种启发式选择方法QV,但是这种方法只能应用于成员系统较少时。
由几何框架[9]理论可知,只有满足差异性和互补性的结果列表才能有效地提高融合性能。本文提出了一种基于变色龙层次聚类[10]和序列前向的成员系统选择算法(RFS),该算法首先定义检索结果列表之间的相似度度量,得到的距离矩阵后用于变色龙层次聚类,然后采用贪婪策略选出k 个来自不同簇的成员系统用于数据融合。
2 相关理论
2.1 数据融合技术
数据融合[11]就是一种能够把多个信息检索系统返回的结果合并,重新排序生成一个性能更优的检索结果的技术,使用合适的数据融合方法能够有效地提升检索性能。将参与融合的检索系统称之为成员系统,成员系统对查询进行检索产生成员结果。数据融合的基本流程如图1所示。
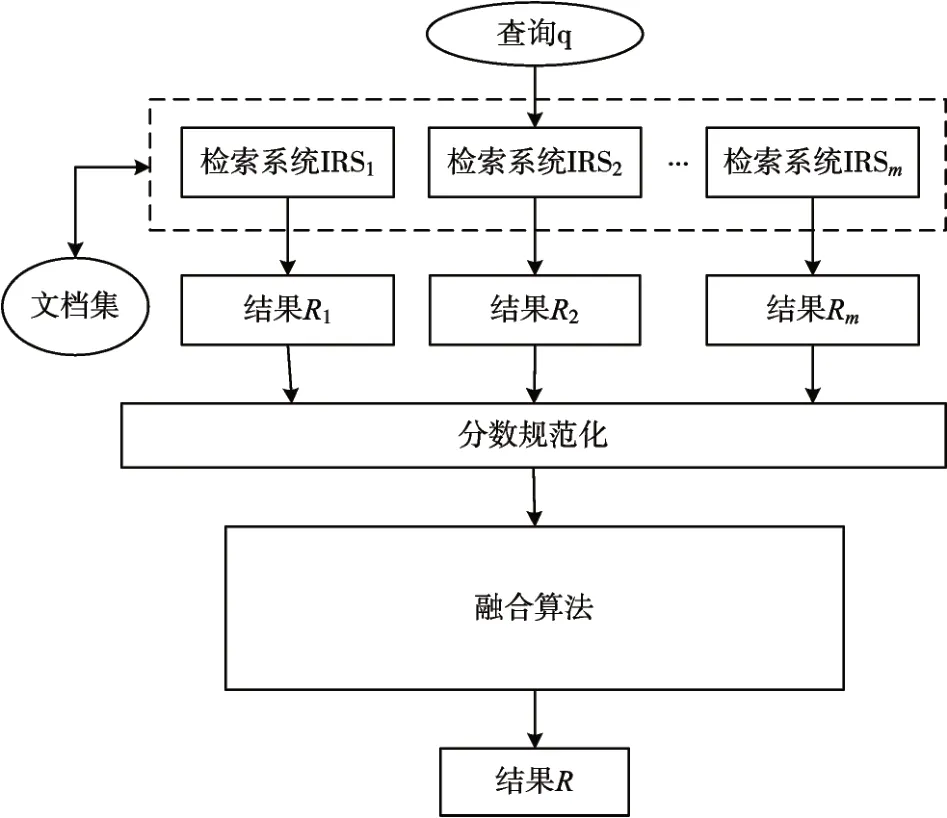
图1 数据融合基本流程
对于用户查询q,在给定文档集中含有m 个成员系统,根据各自的检索策略搜索与查询相关的文档,返回各自的结果列表R1,R2,…,Rm。接下来对着m个结果进行规范化[12]操作,之后使用某种融合算法将m个规范化后的检索结果合并、重排生成最终检索结果。本文采用常用的数据融合方法CombSUM、CombMNZ和MR[13]进行融合操作。
2.2 成员结果列表相似度测定
在信息检索领域中,某些情况下我们需要度量两个检索列表的距离,或者说相似程度[14]。本文采用基于集合的度量[15](Set Based Measure)来衡量结果列表之间的相似度。
基于集合的度量主要通过计算两个不同排序列表,在不同深度时对应集合的交集大小来计算排序列表的相似度。计算出不同深度的交集比例后,通过交集比例的分布来量化两个列表的相似程度,最简单的方法就是直接计算交集比例的平均值。但是随着列表长度的不断增加,距离值有可能会无穷大。同时,在比较两个排序列表的相似性时,要考虑不同位置的元素权重,尤其是top 元素的相对位置权重。为解决上述问题,我们给每个深度的交集比例定义了一个权重系数,计算加权和,称为偏差重叠排名(RBO)。设S 和T 为两个无限长度的排序列表,Si为列表S 的第i 个元素,Sc:d={Si:c≤i≤d}表示列表中从位置c到位置d的所有元素组合的集合。在深度为d 时,列表S 和T 的交集为

交集的元素个数称之为列表S 与T 在深度为d时的交叠,该交叠相对于深度d 的比值称之为列表S与T的一致度。

则RBO距离度量定义为
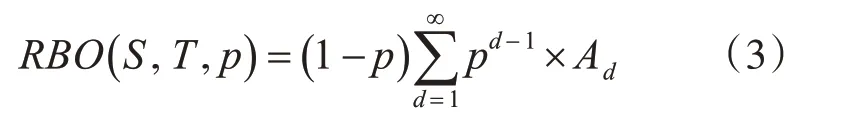
其中,p为一个预先定下的参数,0 <p<1。
2.3 变色龙层次聚类
变色龙聚类是一种利用动态模型的两阶段层次聚类算法,其考虑不同簇间的信息,克服了传统层次聚类静态建模的局限性[16]。变龙算法的聚类步骤如图2。

图2 变色龙聚类步骤
第一阶段,首先Chameleon 计算数据集的距离矩阵和相应的权重矩阵,然后采用KNN 方法来构建一个稀疏图,图的每一个顶点代表一个数据对象,如果一个对象是另一个对象的k 个最相似的对象之一,那么这两个顶点(对象)之间就存在一条边(这些边加权后反映对象间的相似度);最后,Chameleon使用hMetis图划分算法,把k-个最近邻图划分成大量相对较小的子簇,使得边割最小。
第二阶段,计算子簇两两间相对互连度RI 和相对近似度RC,并以此计算其相似度F,迭代选取相似度最大的两个子簇合并,直到子簇个数小于设定值或相似性最大值小于阈值时结束。相对互连度RI和相对近似度RC的公式如下所示:


3 本文算法
本文针对大规模数据集,首先在数据预处理阶段将不正常数据对象去除,生成初始数据集,利用变色龙聚类算法将数据集依据相似性分成若干簇,之后采用贪婪策略顺次从不同簇中挑选出若干融合性能好的成员结果,最终找出最佳成员系统组合。
算法1 基于变色龙层次聚类的分组算法


4 实验结果及分析
本文采用的TREC(Text REtrieval Conference)提交的结果作为数据集,采用的数据集为
TREC2017 Precision Medicine Track Scientific Abstracts Task,此数据集中含有125 组检索结果,远多于其他的主题数据集,有利于测试选择方法的可靠性。经过初步挑选后有108 个成员系统检索结果可用。
在聚类完成后,使用二折交叉验证将每组成员系统中的查询按编号分为奇偶两组。首先,使用贪婪策略将簇中偶数组使用顺序前向算法选择出成员系统组,之后将其在对应成员系统组中的奇数查询上进行融合测试,使用CombSUM 作为来计算评价指标,然后再反过来测试。实验中采用分别用CombSUM、CombMNZ、MR 作为选择后融合方法,MAP 值作为融合性能评价指标。实验共分为两个部分。
1)小规模数据集选择算法性能对照实验
文献[7]提出的QV 选择算法只适合在参与融合的成员系统较少时,为了与本实验提出的RFS算法进行对照,故从实验集截取了MAP 值较优的50个成员系统进行实验。实验中RFS 方法将成员系统分成10 个簇,依次选择2~10 个成员系统。之后使用分别CombSUM、CombMNZ、MR 进行融合实验。AllList 表示所有成员系统参与融合后的结果。实验结果如图3所示。

图3 RFS选择算法与QV选择算法的性能曲线图(评价指标MAP)
分析图3发现,随着选择系统个数的增加,RFS算法和QV 算法的性能都先增加再降低,在选择的成员系统个数为6 左右时取得最佳性能,且RFS 算法的性能远由于QV算法。
2)RFS算法在大数据集上的性能实验
为了说明RFS算法在大规模数据集上的效果,本节实验使用含有108 个成员系统的数据集来测试,经过试验测试,数据集被分成21 簇个数,故选取不同的组数(从2 组~21 组)进行融合实验,同时引入了其他几种选择算法。GA是使用遗传算法来选择成员系统;TopIR 选择算法,根据MAP 表依次选取MAP 值较大的成员系统参与融合;TopCha 选择算法则是在完成聚类后,依次选取每个簇中MAP值最大的成员系统参与融合;Bsetcomb是RFS选择的成员系统进行融合之前最优成员系统性能。将这四种算法分别运用在实验数据集上,并分别使用CombSUM、CombMNZ、MR 作选择成员系统组的融合方法。结果如图4~6所示。
观察图4、图5、图6可以得出,在所有提出的选择算法中,随着选择的成员系统增加,融合性能也逐步提升。其中性能最好的是RFS 选择算法,Top-Cha 选择算法次之。在使用CombSUM、CombMNZ、MR 进行融合时,RFS 分别在成员系统个数n=15、16、16时MAP取得最大值0.3607、0.3451、0.3608。
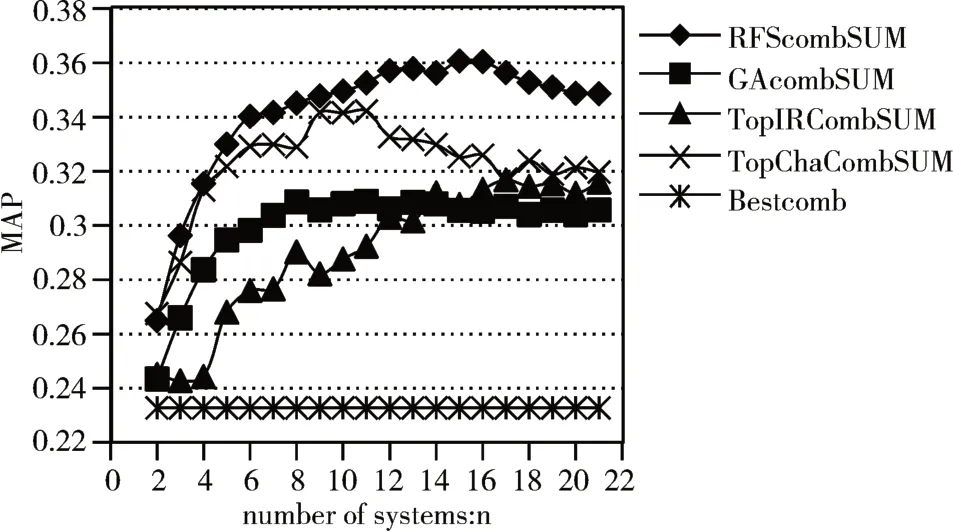
图4 不同选择算法情况下的融合曲线图(融合方法:combSUM)

图5 不同选择算法情况下的融合曲线图(融合方法:combMNZ)
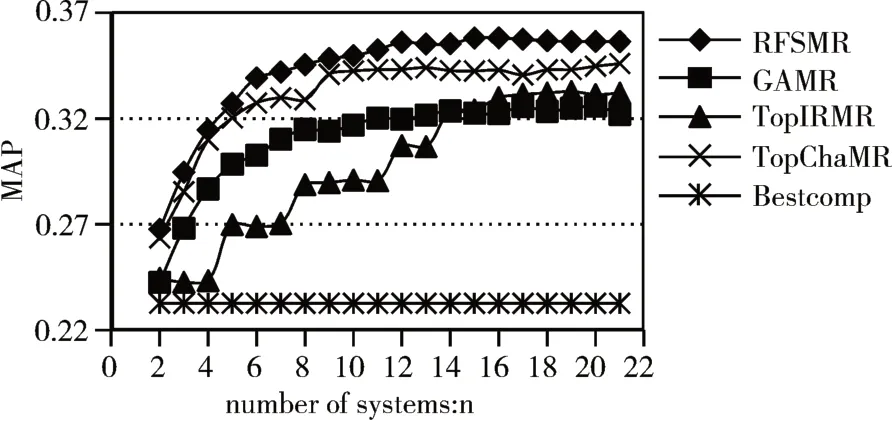
图6 不同选择算法情况下的融合曲线图(融合方法:MR)
将其与所有成员系统结果融合的结果(All-List)进行对照,如图7 所示,通过RFS 选择算法得到成员结果列表融合后的性能高于所有成员结果列表的融合性能,同时个数大大较少,因此有效地降低了时间复杂度,提升了融合效率。
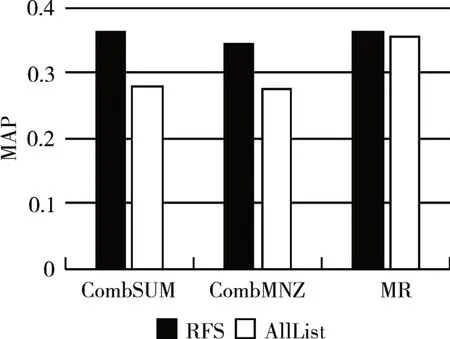
图7 选择成员系统和所有成员系统融合的性能比较
5 结语
本文提出了一种新的成员系统选择算法,通过上述实验表明该算法通过降低成员结果的冗余度,不仅能大大缩减参与融合的成员系统个数,而且这些选择的成员系统结果融合后性能也明显提升,同时本算法也明显优于其他的选择算法。下一步研究重点是如何改进聚类算法,从而使簇间的成员系统相似度更低,以有利于下一步的筛选。
