改进小波阈值算法在染液浓度检测中的去噪研究*

陆 蓉 王 直

（江苏科技大学电子信息学院 镇江 212003）

1 引言

自动染色机是一种对贴附于载片玻璃上的切片自动染色的医用设备，避免了人工染色的随意性、染色量小、工作效率低、控制准确度不一致、质量不稳定等缺点。

染液的浓度是影响染片质量的关键因素，载玻片样品浸泡在染色试剂池中染色，每次染色后，池内的染色试剂的浓度都会降低，而染剂价格相对昂贵，频繁更换增加成本、浪费资源，因此需要检测出染液浓度和该浓度下染色效果相对较好的情况下的染色时间。而在真正实验过程中并不是直接测量出染液的浓度，而是运用吸光光度法得到光信号然后再转换成电信号来判断，然而在得到的数据中存在外界的噪声的干扰，选用小波去噪削弱噪声的干扰能力。

对于信号的去噪问题，大家都做了广泛的研究，并都取得了一些研究成果，硬阈值函数和软阈值函数是小波去噪中较频繁使用的函数，常用来和改进型的阈值函数处理信号的能力做对比［1］。众所周知传统的硬阈值函数处理后的信号虽然能较好地保留信号边缘局部特征，但信号存在震荡、不够平滑等问题，而软阈值函数处理后的信号虽解决了硬阈值函数不连续的问题，但存在边缘模糊等失真的现象，使得重构信号与真实信号之间存在一定的偏差，从而导致精确度不高［2］。

由于软硬阈值函数存在一定的缺陷，为了进一步去除信号中的噪声，则需要对算法进行改进，构造出一种新型的小波阈值函数既要综合传统小波软硬阈值函数的优点又要改善其存在的缺点［3～5］。

2 系统整体设计

2.1 光电检测系统概述

医用光电检测系统的工作原理是将稳定的光源透过滤光片照射待测物体，待测物体透射出来的光信号被硅光二极管接收，然后硅光电二极管（S1226-44BQ）将接收到的光信号转换为电流信号经过对数放大模块，对数放大模块的作用是将电流信号再进一步转换为电压信号，采集到的电压信号再通过模数转换，以上实现了浓度到电信号的转换，最终CAN 总线将数据传达给上位机进行信号处理［6］。

图1 是浓度检测模块硬件设计原理图。模数转换器选用的是AD7705，电信号经过信号跟随器将信号电压输入到AD7705 中，AD7705 是16 位的∑-Δ 型AD 转换器，包括由放大器和缓冲器组成的前端模拟调节电路、可编程数字滤波器、调制器，通过传感器直接测量多通道小信号进行AD 转换［7］。

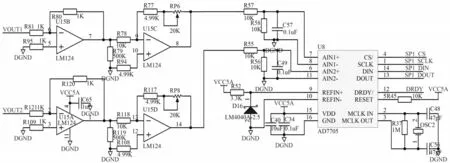
图1 浓度检测模块

2.2 光电检测系统的数学模型

光电检测的数学模型所使用的原理是Lambert-Beer 定律，Lambert-Beer 定律是分光光度法的基本定律［8］，Lambert-Beer 定律是用来描述物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系［9］。

在本文实验中需要测量的是染液对于0.5W 波长为450nm 和780nm 的入射光的吸光的强弱变化情况。

依据Lambert-Beer定律，染液的吸光度可以表示为

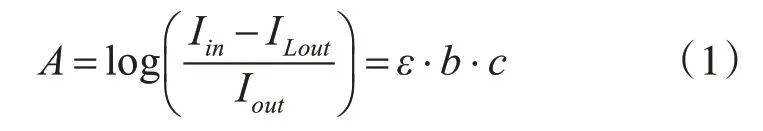
其中，Iin为入射光的强度；ILout为入射光的损耗光强；Iout为透射光的强度；ε为介质摩尔吸光系数；b为吸收层的厚度（即光程）（cm）；c为吸收物的摩尔浓度（mol/L），和染液温度以及照射时间有关，是一个变量［10］。

染液的浓度是影响染片质量的关键因素，因此为保证染色质量的一致，实验在染液的温度为37℃恒温状态下进行，当染液的温度过低时，不利于染色或染色过浅致使染片模糊则容易导致诊断医生的误诊或漏诊［11］，当温度过高，导致浓染，细胞的异型性增加，甚至可能杀死细胞，影响染剂活性，背景着色，使得切片整体不清晰。实验目的是当染液温度一定时，记录染液不同浓度及其浓度下对应的染色时间，经诊断专家对染色切片的评定，保留染色效果较好时的染液浓度和染色时间的数据。用采样信号的电压幅值表示透射出来的光的强度从而体现染液浓度的高低，若染液浓度越高则吸收的光就越多，透射出来的光的强度降低，相反，若染液浓度越低则吸收的光就越少，透射出来的光的强度增强。

3 改进的小波阈值函数

3.1 小波阈值基本原理

小波转换的主要原理就是在小波基的空间里将信号解析并将噪声去除后得到真实信号。一维小波的去噪模型定义如下：

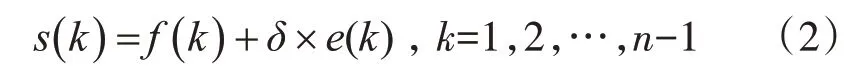
式（2）中：s(k)为含噪声信号；f(k)为真实信号；e(k)为噪声信号。

小波去噪包括小波基选取、确定分解层数、阈值处理和信号重构四个过程，具体流程如图2 所示。

图2 小波阈值去噪过程

1）原始信号的小波分解。不同的原始信号根据其含噪性不同来确定不同的分解次数以及小波基函数。最终计算出不同的小波分解系数［12］。

2）阈值处理。通常采用阈值函数的手段来处理小波分解系数，本文选用传统的软硬阈值函数和改进的阈值函数［13］。

3）信号重构。将经阈值处理过的小波系数进行重构，可得降噪信号［14］。

在光电信号采集的时候，难免会有外界噪声的干扰，一般情况下认为这种噪声e(k)是高斯白噪声。高斯白噪声在时间域上是非连续的。而有效信号具有一定的连续性，所以在小波域中，有效信号的小波系数值必然大于那些能量分散且幅值较小的噪声的小波系数值［15］，于是，确定合适的阈值后，将小波系数根据阈值进行取高去低处理，这样就可以达到去除噪声而保留有用信号的目的。

3.2 改进阈值的小波去噪方法实现

小波阈值去噪算法的核心是选取合适的阈值和阈值函数，阈值函数的构造对于小波去噪整体而言十分重要，很大的关系到信号去噪的质量［16］。

Donoho等提出一种对小波阈值λ的确定方法［17］，如式（3）所示：

在应用研究中一般取：

式（3）中，N为信号长度；式（4）中，σ为噪声的方差；w为原始小波系数。

硬阈值函数定义如下：

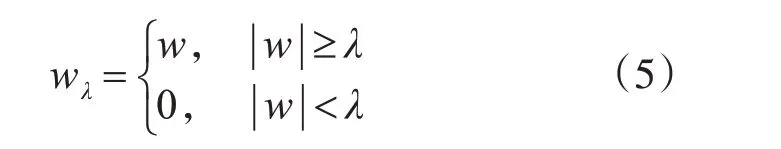
当小波系数的绝对值大于给定的阈值时保持不变，当小波系数的绝对值小于给定的阈值时令其为零［18］。

软阈值函数定义如下：

当小波系数的绝对值大于给定的阈值时令其减去阈值，当小波系数的绝对值小于给定的阈值时令其为零。

式（5）和式（6）中，w为含噪信号处理前的小波系数；wλ是降噪后的估计小波系数；λ为阈值。

软、硬阈值函数被广泛应用到研究领域之中，但是这两种传统算法存在很大的不足。硬阈值算法中wλ在 |w|=λ处间断，从而使信号出现Pseudo-Gibbs现象，重构信号因此会变得不平顺。软阈值函数较硬阈值函数而言有更强的连续性，信号更加平顺，但是wλ和w之间存在恒定偏差，给重构信号带来一定的误差［19］。

现对传统阈值算法进行改进，基于软阈值函数，提出了如下的改进的阈值函数：

3.3 实验结果分析

将实验采集到的10000 个采样信号的数据导入至Matlab 中，经过多次实验，选取了最优分解层数为3层，小波基为sym5，在相同的条件下，分别用本文提出的阈值函数以及传统的软硬阈值函数进行仿真和对比［23］，初始信号、硬阈值函数处理后的信号、软阈值函数处理后的信号、新阈值函数处理后的信号如图3～7所示。

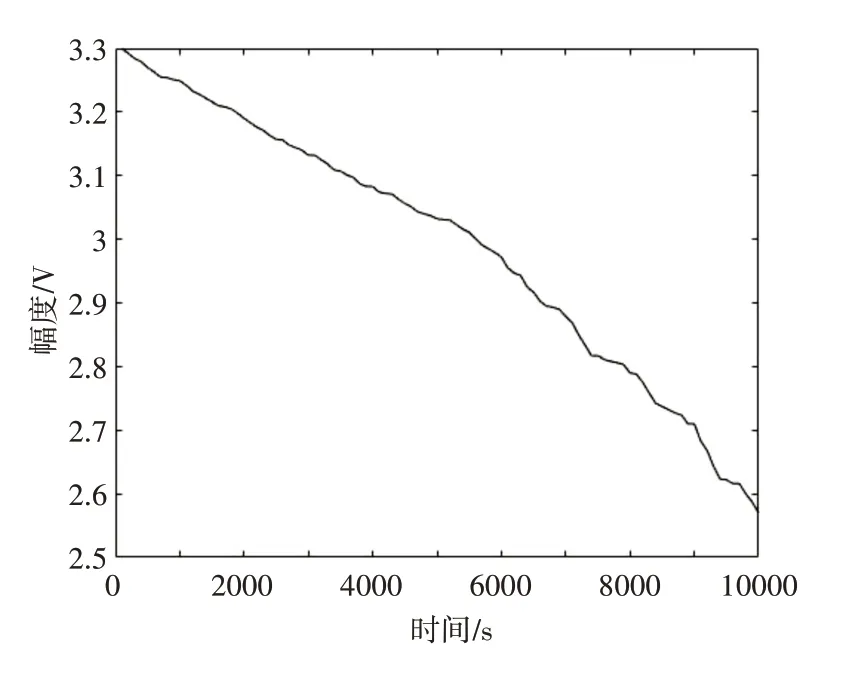
图3 初始信号

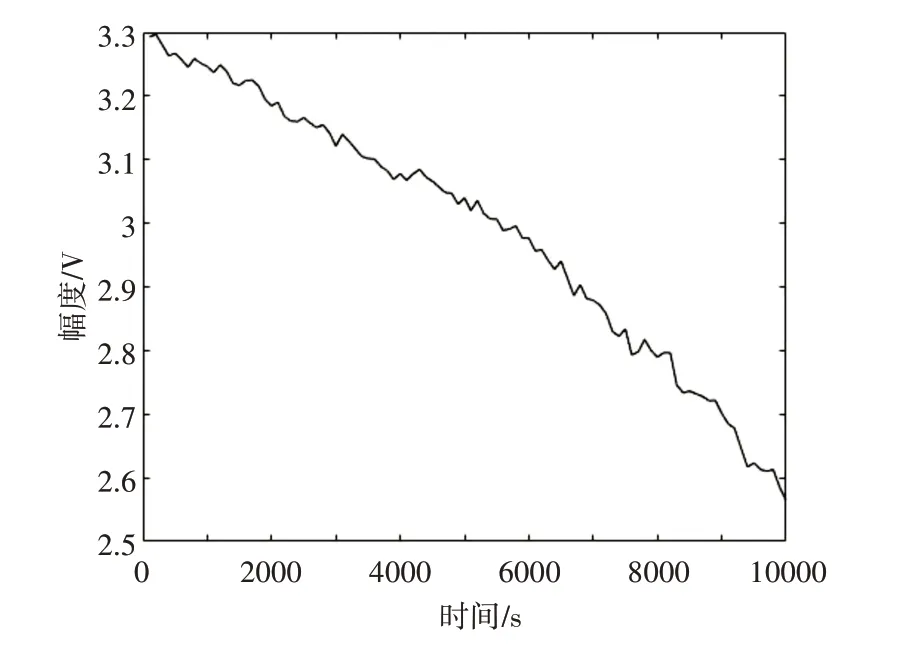
图4 加入噪声后的信号

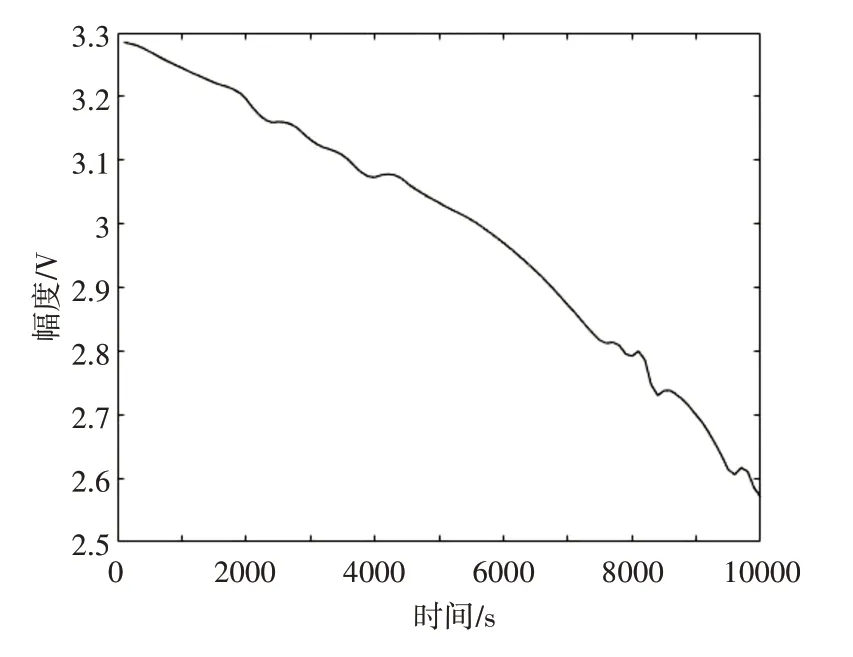
图5 硬阈值函数处理后的信号

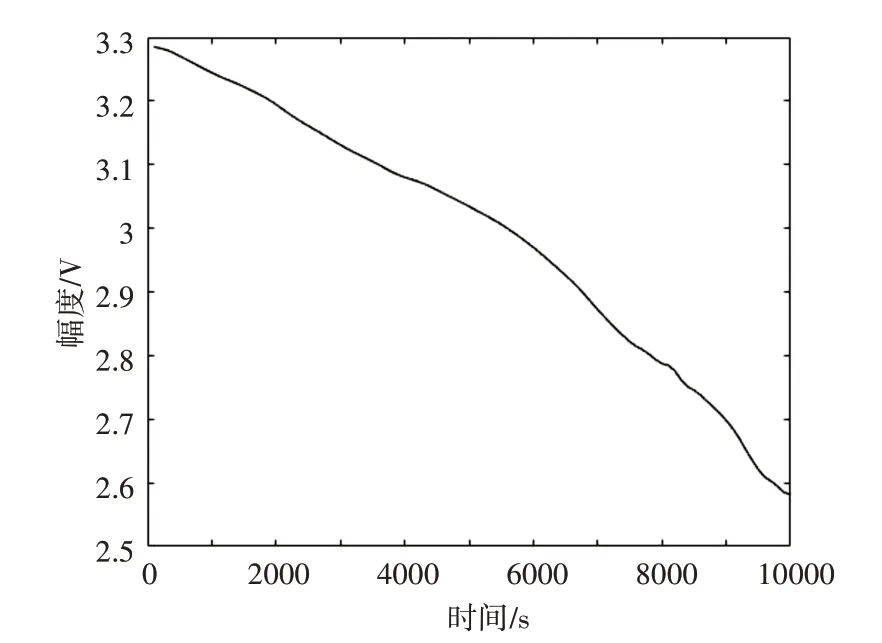
图6 软阈值函数处理后的信号

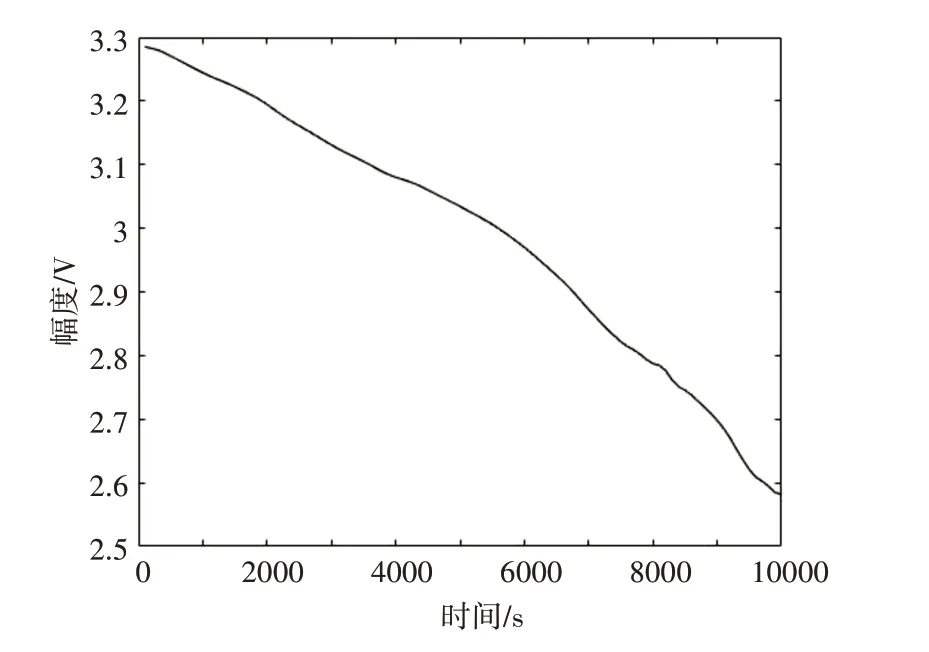
图7 改进阈值函数处理后的信号

为了更好地区分不同阈值函数的去噪效果，将信噪比（SNR）和均方误差（MSE）作为去噪性能的判定标准。

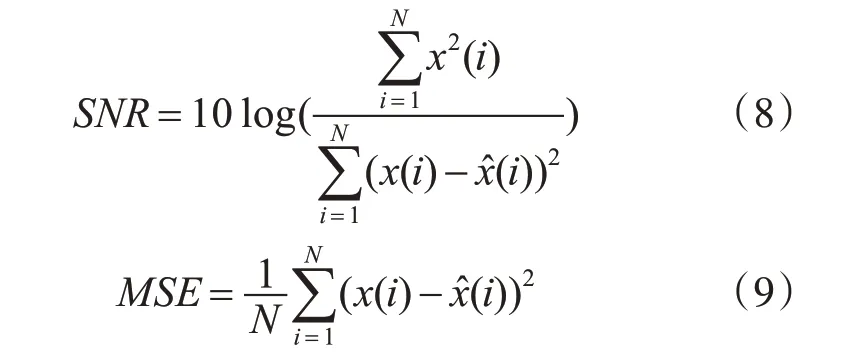
式（8）和式（9）中，x(i)为原始信号，x^(i)为去噪后重构信号，N为采样长度。

不同阈值函数处理信号仿真得到的信噪比和均方误差如表1所示。

表1 不同阈值函数的去噪效果对比

从表1 结果来看，本文所采用的的算法相较于传统算法SNR 更高而MSE 更低，能达到较优去噪结果。

4 结语

本文旨在于研究在染液浓度检测系统中如何运用小波阈值去噪算法将光电信号中的噪声优化去除。为获得更理想的信号去噪效果，在原有阈值函数的基础上提出了一种改进的阈值函数，该函数避免了传统的软硬阈值算法中存在的问题，即硬阈值函数处理后的信号不够平滑，但保留了硬阈值函数精度高的优点，更好地保留了信号的有用信息，软阈值函数处理后的信号不够精确，但保留了软阈值函数连续性好的优点，有较好的降噪效果和灵活性，从信噪比（SNR）和均方误差（MSE）这两个去噪指标验证了本文改进阈值函数的有效性，具有一定的实用价值。