基于全基因组关联研究的tag SNP 预测方法的研究与分析*

刘高伟

（中国石油大学（华东）计算机与通信工程学院 青岛 266580）

1 引言

全基因组关联研究［1］（Genome-Wide Association Study，GWAS）在全基因组层面上，通过大样本、多中心、反复验证的方法来寻找大规模群体的各种脱氧核糖核酸（Deoxyribonucleic acid，DNA）遗传标记［2］，如单核苷酸多态性（Single Nucleotide Polymorphism，SNP）［3］或 基 因 拷 贝 数 变异（Copy Number Variations，CNV）［4］等与复杂疾病相关的遗传因素，从而全面揭示与人类疾病发生、发展和治疗相关的遗传基因。全基因组关联研究中的单核苷酸多态性（single-nucleotide polymorphism，SNP）是指基因组DNA 序列同一位置单个核苷酸变异所引起的多态性，其占人体基因组遗传多态性的90%以上［5～7］。SNP 集分析方法在识别致病SNP 时有较高的功效，且越来越受到生物医学界的关注［8～9］。

理论上，在寻找遗传疾病相关基因的过程中，是要通过对所有SNP 位点进行鉴定，然而，人体基因中一共有300 万个SNP，对所有SNP 位点进行基因分析，这样将消耗大量成本［10～13］。研究表明，许多SNP 位点之间具有一定的关联关系，其中部分SNP 位点信息就可以代表所有SNP 位点所携带的信息，我们将具有代表性的SNP 成为标签SNP（tag SNP）集［14～16］。通过对tag SNP 集进行基因分型，tag SNP 集的质量与基因分型的准确率有密切的关系，因此tag SNP 集评估方法已经成为GWAS 研究领域的热点研究内容［17］。

评估tag SNP 集质量是SNP 集分析中的一个重要内容，高质量的tag SNP 集可以更好节约基因分型成本，并且提高基因分型的准确率。2005 年，Halperin 等［18］提出了STAMPA 方法评估tag SNP 集质量，该方法在预测过程中使用了容易获得的基因型数据，而不是单倍体数据，并且该方法预测过程不受单倍体块划分限制，对每一个非tag SNP 位点进行预测，以此达到评估tag SNP集质量的目的，该方法在预测非tag SNP时只考虑了与所需预测的非tag SNP物理距离最邻近的tag SNPs，而没有考虑到SNP 之间的生物距离，这样也就导致预测效率不高；Ilhan 等［19］使用支持向量机（Support Vector Machine，SVM）方法对所选择的tag SNP 进行预测，通过粒子群优化方法对支持向量机中的参数进行优化，使用遗传算法（Genetic Algorithm，GA）选择tag SNP，通过每一次迭代对参数进行优化，以使得SVM 方法更加有效，该方法在预测tag SNP集时，通过每一次训练调整参数，在预测时需要所有tag SNPs 位点信息，并且需要迭代的次数要足够大，这样才可以有较好的评估tag SNP 集；Mauawad 等［20］基于SNP 之间的连锁不平衡度，提出Linkage Coverage 方法评估tag SNP 集质量，使用所有tag SNPs预测non-tag SNP，充分考虑了SNP 之间的关联关系，然而该方法只计算了tag SNP 集与tag SNPs 集之间的连锁不平衡，没有考虑SNPs之间物理距离，这样也就降低tag SNP集的评估质量。

基于上文所提出的问题，本文提出一种基于连锁不平衡度的Genetic-majority dominance（GMD）tag SNP 预测方法评估tag SNP 质量，GMD 通过使用遗传方法迭代选择出tag SNP 集，然后以SNP 之间的连锁不平衡为基础，充分考虑了SNP之间的关联关系以及实际生物距离，在使用tag SNP 集预测非tag SNP集时，并不需要使用所有tag SNP，只需要找出与所需预测的non-tag SNP 集关系最为邻近的tag SNPs，所使用的也是易获得的基因型数据，GMD 可以定量分析tag SNP 集质量且也保证了评估效果。

2 基于连锁不平衡度的GMD方法

2.1 连锁不平衡度

连锁不平衡是指不同位点上两个等位基因出现在同一个染色体上的频率要高于预期的随机频率的现象［21］。由于Human Leucocyte Antigen（HLA）不同基因位点的某些等位基因经常连锁在一起遗传，而连锁的基因并非完全随机地组成单体型，有些基因总是较多地在一起出现，致使某些单体型在群体中呈现较高的频率，从而引起连锁不平衡。

设群体有n 个个体，每个个体有p个SNP 位点，即原始SNP 集中有p 个SNPs，记原始SNP 集为L=｛1，2，…，p｝。因为人类是二倍体生物，所以共有2n 个 单 体 型，令zi=(zi1，zi2，…，zip) ，i=1，2，…，2n，Rij表示SNPi与SNPj的连锁不平衡度，通过下式可得［22］：

2.2 遗传算法-多数占优方法（GMD）

遗传算法-多数占优方法（GMD）是将遗传算法与多数占优原则结合的一种tag SNP 集预测方法，该方法使用遗传算法选择出tag SNP集，然后以多数占优原则为基础评估tag SNP集的质量。

遗传算法是一种基于“适者生存”的高度并行、随机和自适应的优化算法，通过复制、交叉、变异将问题解编码表示的“染色体”群一代代不断进化，最终收敛到最适应的群体，从而求得问题的最优解或满意解［23～24］。在本文中，使用遗传算法从原始SNP集中选择出tag SNP 集。使用tag SNP 集对非tag SNP 进行预测时，对样本基因数据进行训练，得到数据之间的关系，然后根据多数占优原则使用所选择的tag SNPs预测非tag SNP集。

3 算法描述

3.1 符号定义

设群体有n 个个体，每个个体有p个SNP 位点，即原始SNP 集中有p 个SNPs，记原始SNP 集为L=｛1，2，…，p｝。设一个p 维向量gi=｛0，1，2｝p表示一个基因片段，每一个位点上取值为0，1，2。0，1分别表示次等位基因和主等位基因，2 表示杂合子基因，prei表示在i位置上得到的预测值。每一个基因片段是由两个单体型组成，单体型中每一个位点上的取值为0 或1。设gij所表示的是第i 个基因片段上第j个位置上的基因型信息，使用hij1与hij2表示组成该基因的两个单体型对应位点上的单体型值，hijp∈0｛0，1｝，如果hij1=hij2=1，gij=1，如果hij1=hij2=0，gij=0，如果hij1≠hij2，则gij=2。

T 表示tag SNP 集，|T|表示tag SNP 集中元素的个数，即tag SNP的个数。

3.2 遗传算法选择tag SNP集

3.2.1 染色体编码方案

使用二元向量表示tag SNP 选择问题的染色体，使用Ci=｛0，1｝p表示一个染色体，0 表示non-tag SNP，即非tag SNP，1 表示tag SNP。所使用的样本数量一共是n 个，所以有Ci=｛ci1，ci2，…，cip｝，cij的取值为0或1，i=1，2，…，n，j=1，2，…，p，设每一个染色体中有k个tag SNP，即有k个值为1。

3.2.2 选择

计算每一个染色体的适应值，即tag SNP 集预测non-tag SNP 集的预测精度值pv（具体预测方法在下节介绍），这样每一个染色体就有一个对应的pv，按照pv从小到大进行排序，C'=｛C1'，C2'，…，Cp'｝。设 两 个 参 数Wup（Wup＞1）和Wdown（Wdown＜1），d=（Wup-Wdown）/p-1，令Rank（Ci'）=Rank（C1'）+（i-1）*d。设阈值t0，如果Rank（Ci'）＞t0，则选择Ci'，且将Rank（Ci'）=Rank（Ci'）-1；在0-1 之间随机产生一个分数f1，如果Rank（Ci'）＞f1，则将Ci'选择，否则不选择，一直进行该操作，一直选择出n个染色体。

3.2.3 交叉

选择操作完成之后，进行交叉操作，再本文中使用的是两点交叉，设交叉率为Xrate，判断染色体Ci'与Ci+1'之间是否需要进行交叉，需要在0～1 之间随机产生一个分数f2，如果Xrate＜f2，则不进行交叉操作，否则，将染色体Ci与Ci+1进行交叉操作，交叉过程为：随机产生两个整数r1与r2，1 ≤r1≤r2≤p，将染色体Ci与Ci+1的区间［r1，r2］之间的片段进行交叉操作。

3.2.4 突变

突变操作：对于每一个染色体的每一个SNP进行突变操作，设突变率为Mrate，判断SNP 是否需要突变，在0～1 之间随机产生一个分数f3，若f3＞Mrate，则不发生突变，否则将SNP 位点进行突变操作，即该位点信息本来为0，则变为1，如果是1，则突变为0。

3.2.5 修复

事先设置的tag SNP 个数为k，在经过选择，交叉，变异操作之后，为了保证tag SNP个数为k，需要进行修复操作，对于每一个染色体有t 个tag SNP，如果t＞k，则随机选择t-k 个tag SNP 将其值改为0，如果t＜k，则随机选择t-k 个non-tag SNP 的值改为1。

在修复操作完成之后，使用预测算法对每一个染色体中的non-tag SNP 进行预测精度。若迭代次数未达到总次数，则继续迭代，否则停止。

3.3 tag SNP预测算法

4 结果与讨论

4.1 数据描述

在实验中，一共使用了四组数据集：包括了HTR2A 基因、ASAH1 基因、OLMF4 基因和PHGDH基因数据集。

HTR2A 是13 号染色体上与精神分裂症、强迫症等疾病有关的基因，该基因位于13 号染色体位置q14-21，一共有169个SNPs在基因HTR2A上。

ASAH1 是8 号染色体上与法伯脂肪肉芽肿病疾病有关的基因，该基因位于8 号染色体位置8p22，一共有177个SNPs。

OLMF4 是13 号染色体上与胃癌、胰腺癌等疾病有关的基因，该基因位于13 号染色体位置q14.3，一共有56个SNPs。

PHGDH 是1 号染色体上与癫痫疾病有关的基因，该基因位于1 号染色体位置1p12，一共有64 个SNPs在基因PHGDH。

实验中，对于每一个数据集使用HAPGEN2 软件产生1000 组模拟数据，每一组数据中有500 个case个体，仿真数据的连锁不平衡结构是基于Hap-Map计划产生的。

4.2 实现环境

在实现本方法时，所使用的编程语言是R 语言。所运行的环境是在Linux 操作系统下运行的，所使用的PC 的设施要求4GHz的内存以及500G 的硬盘存储空间。

4.3 预测精度比较

在实验中，设置遗传算法的最大迭代次数为50，参数Wup=1.2，Wdown=0.8，交叉率Xrate=0.8，突变率Mrate=0.1，在对HTR2A 和ASAH1 数据集进行实验时，tag SNP 的 个 数 从5 递 增 到30，对OLMF4 和PHGDH 数据集进行实验时，tag SNP 的个数从3 递增到10，每一次递增数量为1。

在本文中，首先使用遗传方法选择出每一次迭代所产生的tag SNP 集，然后通过使用不同tag SNP预测方法衡量每一次迭代出的tag SNP 集的质量，得到对应的适应值，将本文中所提出的GMD 方法与STAMPA预测方法进行比较，比较结果图1所示。

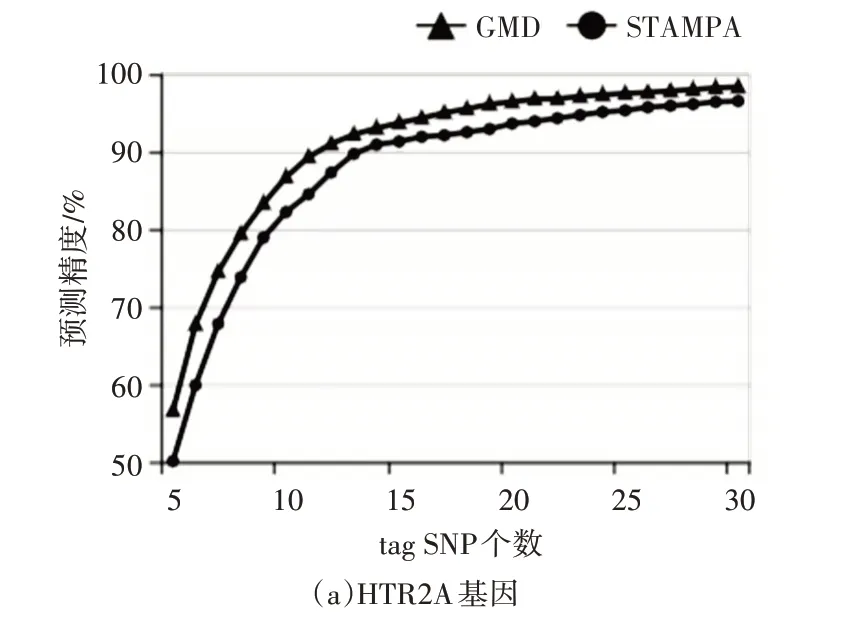
图1 GMD方法与STAMPA方法分别对HTR2A基因、ASAH1基因、OLMF4基因、PHGDH基因进行预测比较图

通过图1 可以看出当tag SNP 的个数比较少时，STAMPA 方法所预测的精度较小，随着tag SNP个数不断增加，预测精度也在逐渐提高，且可以看出本文提出的GMD 预测方法在HTR2A、ASAH1、OLMF4 和PHGDH 数据集中，预测结果都优于STAMPA 方法。STAMPA 方法在预测non-tag SNP时，只考虑了物理距离最短的tag SNPs，而没有考虑到所需要预测的non-tag SNP 与tag SNP 的生物意义，因为在基因片段中存在多个单体型块，使用STAMPA 所选择的tag SNPs 与所需要预测的non-tag SNP不在同一个单体型块，这样tag SNPs与non-tag SNP 之间的关联关系比较弱，使用不在同一个单体型块中的tag SNP 预测non-tag SNP，这样大大降低了预测精度，所以该方法不能很好评估tag SNP 集。而本文所提出的预测方法则是可以充分考虑到了tag SNP 与non-tag SNP 之间的生物距离，而且也保证了与所需要预测的non-tag SNP 关联关系最为紧密的tag SNP，这样在预测时，提高了预测精度，可见与STAMPA 方法比较，GMD 方法可以更好去评估所选择出的tag SNP。

在本文中，也将GMD 方法与Linkage Coverage方法进行了比较，因为Linkage Coverage 方法在评估tag SNP 质量时，是通过计算tag SNP 集与non-tag SNP 集之间的连锁不平衡度之和的覆盖率评估tag SNP 集质量，并没有对具体SNP 位点进行预测，所以不能与GMD 方法进行直接比较，在实验中，通过将Linkage Coverage 方法与GMD 方法作为评估tag SNP 集方法与遗传方法选择tag SNP 集结合，遗传方法迭代达到50 次之后，对所选择的tag SNP 集使用STAMPA 方法预测，然后再对所预测的结果进行比较，比较结果图2所示。

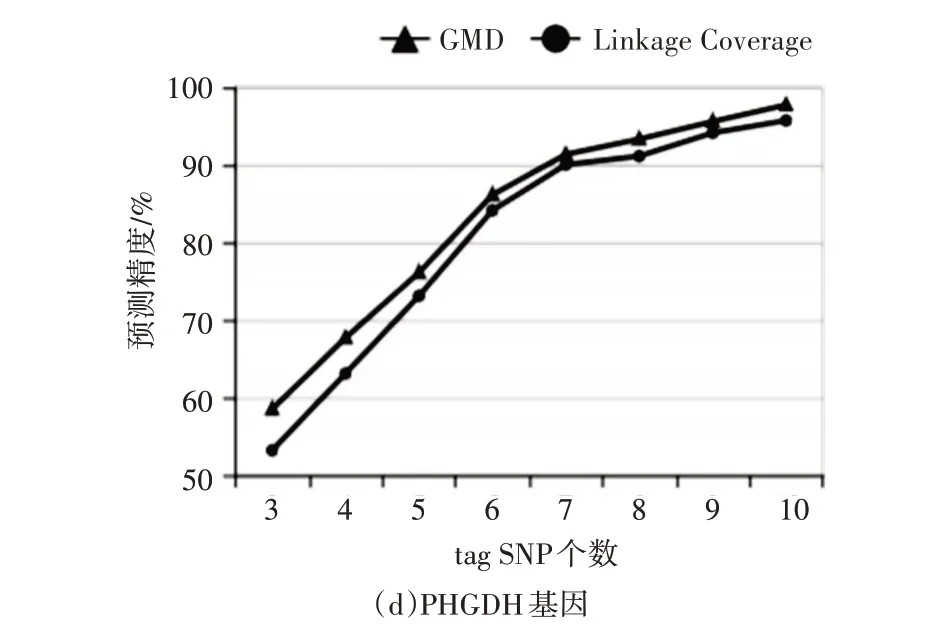
图2 GMD方法与Linkage Coverage方法分别对HTR2A基因、ASAH1基因、OLMF4基因、PHGDH基因进行tag SNP 预测比较图

通过图2 可以看出，在HTR2A 和ASAH1 数据集中，当tag SNP数量较少时，两者之间的预测精度差还是比较少的，但是随着tag SNP数量不断增大，本文所提出的GMD 方法与Linkage Coverage 方法之间的差距越来越大，且一直优于Linkage Coverage 方法。在OLMF4 和PHGDH 数据集，通过图2（c）和图2（d）可以看出本文所提出的方法预测tag SNP 集都是优于Linkage Coverage 方法。因为GMD方法不仅考虑了SNPs 之间的连锁不平衡，而且也使用到了实际样本中的基因型数据，充分考虑了基因型数据之间的关系，这样也就使得GMD 的预测精度比较高。

5 结语

本文提出了一种新的tag SNP 预测方法——GMD 预测方法，该方法通过使用遗传算法选择出tag SNP，然后确定tag SNP 集，通过训练基因型数据，使用多数占优的原则对non-tag SNP 进行预测，这样实现了对tag SNP 的定量分析，将tag SNP 集的质量进行量化分析，该方法在预测tag SNP 集时不仅考虑了SNPs 之间的连锁不平衡度，而且考虑了样本的基因型数据关系，所以GMD 方法可以比较好的评估tag SNP 集。通过将该GMD 与Linkage Coverage、STAMPA 方法在HTR2A、ASAH1、OLMF4和PHGDH 数据集上进行比较，实验结果显示GMD相比于其他两种方法可以更好评估tag SNP 集质量。

尽管GMD 方法可以较好评估tag SNP 集质量，然而，在评估非tag SNP 集时只是使用了与非tag SNP 关联关系最强的两个tag SNPs，没有考虑其他的tag SNPs，尽管其他tag SNPs影响较小，但是其中可能存在潜在的生物意义，所以在接下来的工作中，我们除了使用与所预测的非tag SNP 关联关系最近的tag SNPs，还需要考虑到与需要预测的非tag SNP有潜在生物意义的tag SNPs。