协同定位最小二乘凸性分析
2022-02-16田宇洋顾青涛张任楠张晓博李响戴海亮李成
田宇洋,顾青涛,张任楠,张晓博,李响,戴海亮,李成
(1.北京卫星导航中心,北京100094;2.中国人民解放军75775部队,广东 广州510000)
0 引言
实时高精度位置感知在无人机技术、医疗服务、搜索救援、智能图书馆、自动驾驶等领域中有着广泛的应用。近年来,作为传统无线传感网络(Wireless Sensor Networks,WSNs)定位方法的补充,协同定位受到越来越多的关注。所谓的协同定位是指多用户节点之间的协同,与传统定位方法相比,该方法增加了用户节点之间的几何测量与通信。协同定位算法有很多,基于到达时间(Time of Arrival,TOA)的极大似然估计模型是应用最为广泛的定位模型之一,当测距误差服从高斯分布时,极大似然模型与最小二乘估计模型(Least Square,LS)等价。为了求得该模型的最优解,比较常见的算法为牛顿迭代法或高斯-牛顿迭代法。文献[5]给出了这两种算法的收敛性证明,指出收敛性与代价函数的凸性紧密相关,当目标函数为严格凸时(Hessian矩阵正定),由牛顿算法解算LS模型为强整体二阶收敛。
划分一个优化问题难易程度的分水岭在于其代价函数是凸或者非凸,而LS定位模型的代价函数一般为非凸,因此求解LS定位模型代价函数的全局最优解是困难的,属于NP难问题,目前已有相关研究尝试对这一个问题进行解决。文献[7-8]对单用户定位场景下的LS模型进行了深入分析,提出了代价函数满足全局为凸的条件。LS模型基于最小方差准则(这一准则也是其他定位模型的基础),例如极大似然、加权最小二乘、递推最小二乘等。与此同时,相比递推最小二乘,卡尔曼滤波(Kalman Filtering,KF)模型相当于在两次迭代之间多了状态转移步骤,其核心也是通过最小化方差求得最优估计。因此,对LS定位模型的凸性进行分析具有一定的代表性,其相关结论可以通过最小方差准则推广到其他定位模型。
在协同场景中,当用户节点数量增多时,函数的局部极值点增多,使得迭代算法对初值更加敏感并导致算法不收敛。本文将对协同定位LS模型的凸性进行分析,以深入解释这一现象。
1 无约束最小二乘定位模型
1.1 节点与链路定义
在基于TOA方法的定位场景中,设用户节点个数为,用F={,,…,T}表示其编号的集合,用户节点真实坐标为x∈R,1≤≤,∈N,∈N为定位场景欧几里得空间维度。锚节点的个数为,其编号的集合为F={,,…,A},锚节点真实坐标为s∈R,1≤≤,∈N。设所有节点的集合记为F,则F=F⋃F。在定位场景中,定义任意两点之间的距离观测为一条测距链路,假设某个场景中共有条测距链路,记各个链路编号的集合为={,,…,l}。定位场景中的测距链路可以分为两类:一类为用户与锚节点之间的测距链路(以下简记为AT链路);另一类为协同测距链路(以下简记为TT链路)。设所有链路距离观测值的集合记为D,其中AT链路距离观测值的集合记为D,TT链路距离观测值集合记为D,易知D=D⋃D,D⋂D=∅,并且有|D|=,|D|=,|D|=-。令d是节点编号到点的真实距离,^为两点之间距离的估计值,其中,∈F。
1.2 测距偏差定义
由于信号在传播过程中会受到观测噪声、多径效应以及非视距(Non-Line of Sight,NLOS)传播的影响,观测值不等于节点之间的真实距离,存在测距偏差。设偏差向量为=[,,…,ε]∈R,其中ε表示第条链路上的测距偏差。在视距(Line of Sight,LOS)传播环境中,测距偏差完全由观测噪声引起,其通常满足均值为零、方差为常数的高斯分布,用表示。在NLOS环境中,除了噪声以外还存在一个正偏差,假设此正偏差满足均值和方差都为常数的高斯分布,用表示。基于以上假设,可以对测距偏差建模如下:
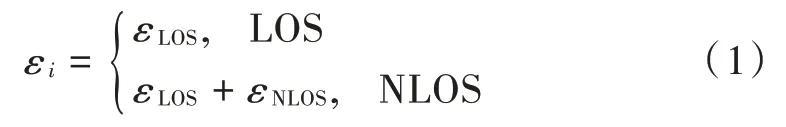

1.3 最小二乘模型定义
在非协同定位场景中,假设有个用户节点,且任意两个用户节点之间无测距和数据交互。考虑某一用户节点T,其位置的真实值为x,令^表示T节点坐标的估计值,则有:

式中‖·‖表示两点之间的欧几里得距离。
若测距链路个数为,分别记为,,…,l,令与之相对应的距离真实值与估计值分别为d和^,且有:
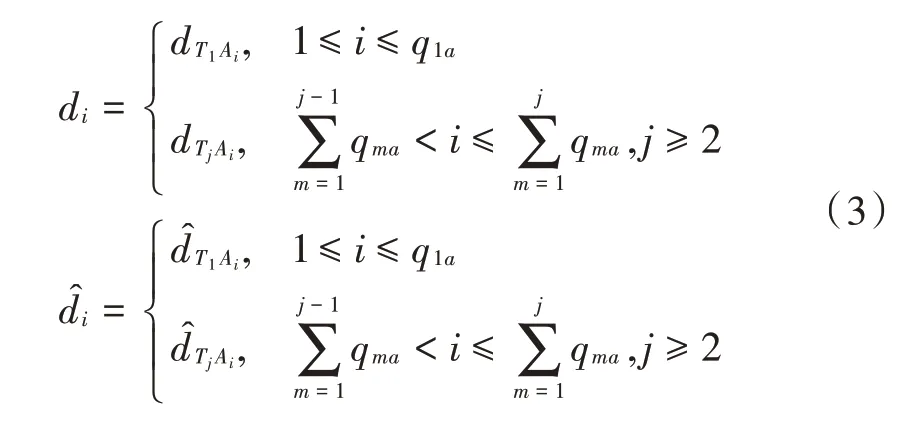
式中:1≤≤,∈N;q是与节点T相连接的链路个数。设距离观测值为ρ∈D,1≤≤,∈N,如果考虑偏差的存在,由定义可知,距离观测值与真实距离之间的关系为:

那么非协同场景中无约束LS估计模型可以表示成如下形式:
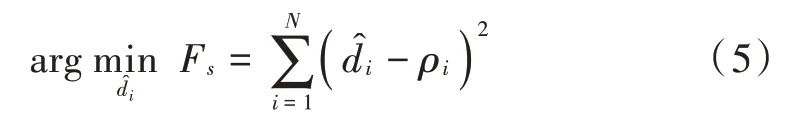
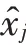

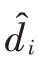
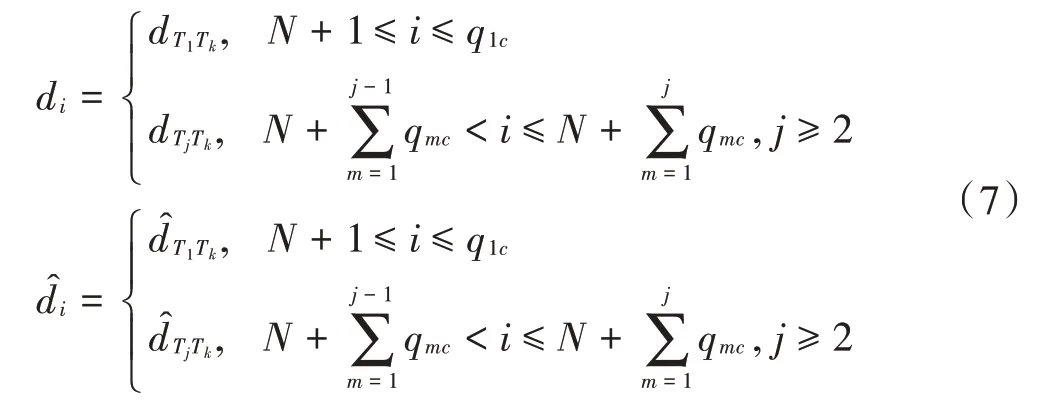
式中:q是链路端点为T T且满足>的TT链路个数,T∈U,>,≥2,U为与T之间存在测距链路的用户节点的集合,其元素下标按由小到大的顺序进行排列。令T为U中第个元素,且的值按照式(8)进行计算:

设ρ∈D,1≤≤,∈N为距离观测值,其与真实距离之间的关系满足式(4)。在此基础上构建协同场景无约束LS模型为:
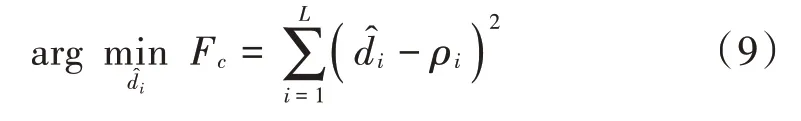
在本文中统一称F和F为LS定位代价函数并且将其记为。
2 模型的非凸性分析
2.1 非协同定位场景分析
为了便于分析且不失一般性,本文选取=2。由凸分析相关理论可知,函数的凸性与其Hessian矩阵密切相关,并且有如下定理成立:
定理1:函数为凸的二阶条件。假设的函数二阶可微,定义域dom为凸集且Hessian矩阵存在,则函数在dom中为凸的充要条件为:对于∀∈dom,其Hessian矩阵为半正定矩阵。
首先求取代价函数F的梯度(一阶微分)和Hessian矩阵(二阶微分),计算结果分别如下:

运用定理1可以得出以下推论:


引理1:实对称矩阵的特征值均为实数。
引理2:实对称矩阵是半正定矩阵的充要条件为其所有特征值非负。

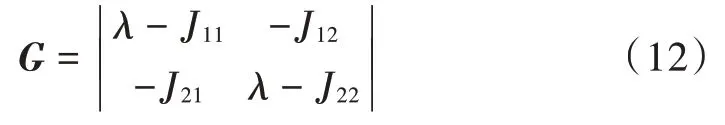
令=0,可以得到特征多项式方程为:

式(13)为一元二次方程,由引理1可知,此方程必存在2个实根,即根的判别式≥0恒成立,函数有2个非负实根的充分必要条件为:

推论2:所有满足不等式组(14)条件的^的集合为。
推论2是LS代价函数为凸的一个等价条件。然而,由于不等式组(14)的非线性特征,使得对该不等式组分析变得比较困难。下面将针对一类特殊的情况进行讨论,并且作出简要证明。
命题1:存在一个集合,若该集合中所有估计值^均满足^-ρ≥0,则在此集合中最小二乘代价函数F为凸,且满足⊆。

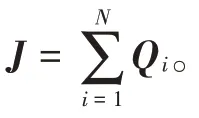
其中:

对Q求特征值,令:

化简得:
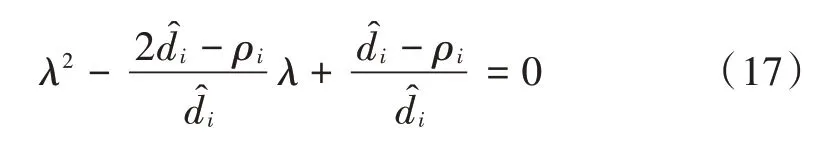
因式分解可求得的2个根分别为:
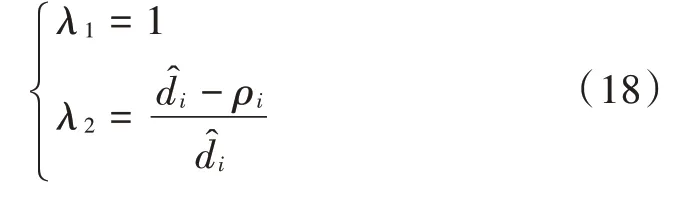

命题1实际上是F局部为凸的一个充分不必要条件,F的非凸区间会随着ε的增大而减小,且当满足ε>0的测距链路数量增多时,F的非凸性也会增强。
2.2 协同定位场景分析


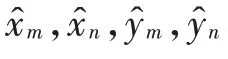
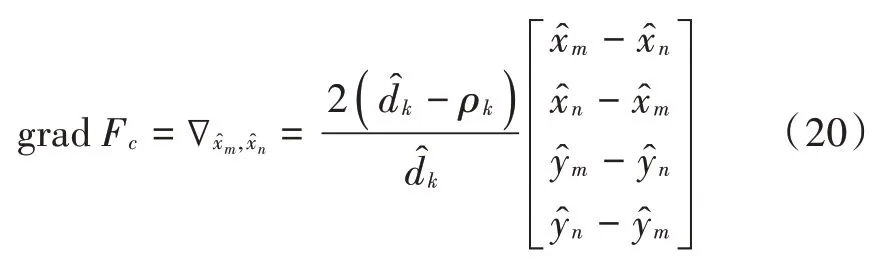
则Hessian矩阵为:

求取的特征值,通过计算可以求得其特征多项式为:
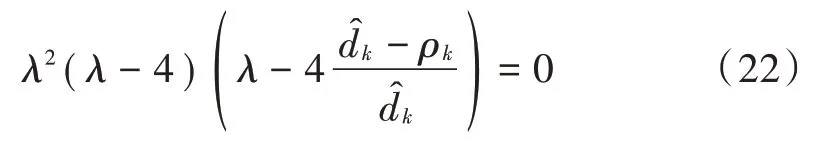
可以解得其4个特征值分别为:

由式(23)可知,当^-ρ≥0时,≽0。接下来做进一步地推广,证明当LS代价函数中同时具有两种测距链路时,这一性质仍然不变。

引理4:相似矩阵具有相同的特征值。
若测距链路位于锚节点与待定位节点之间,则Q的元素位于对角线和与之相邻的位置上,且元素的个数为4,将Q中的4个元素全部平移至左上角。设变换后的矩阵为′,易知Q与′为相似矩阵。由引理4可知Q与′具有相同的特征值。设′=-′,为了求取′的特征值,对′作如下分块:

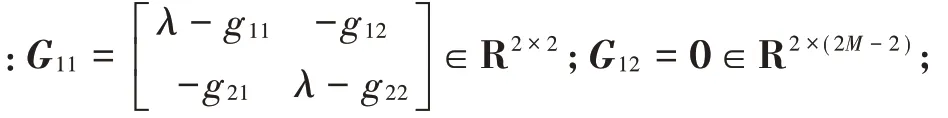
由分块矩阵行列式定理可知:
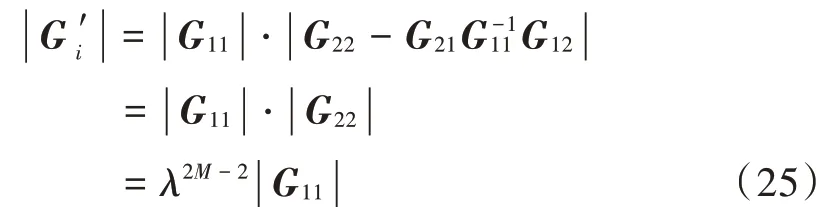

若测距链路位于两个待定位节点之间,易知Q中的元素个数为16个,将其中各个元素全部平移至左上角,将其记为′,设′=-′。同样地,对′进行分块:

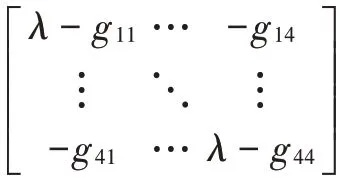
由分块矩阵行列式定理可知:
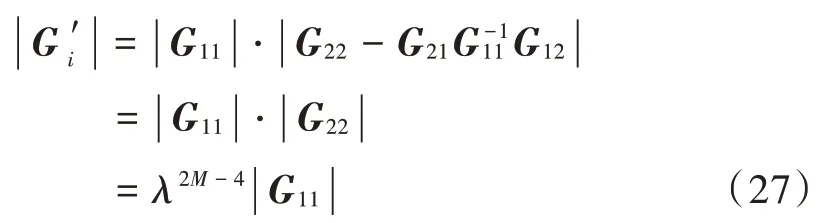


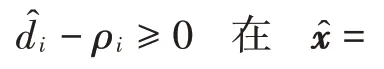

3 仿真验证
3.1 仿真场景设定
在二维平面内建立笛卡尔坐标系,表1给出了非协同与协同场景各个锚节点的平面坐标。本节将对三种偏差环境进行仿真,分别为NLOS环境、LOS环境以及测距偏差为负的情形。每一个场景在各种情况下的偏差大小如表2和表3所示。

表1 各锚节点笛卡尔坐标 m

表2 非协同场景测距偏差 m

表3 协同场景测距偏差 m
3.2 凸性验证
首先对F作全局仿真。考虑测距误差不同的情况下代价函数F的凸性,作出其函数图像、Hessian矩阵的正定图像以及选取不同初值的迭代情况,仿真结果如图1~图3所示。
图1分别显示了NLOS环境、LOS环境以及测距偏差为负的环境下LS代价函数图像。
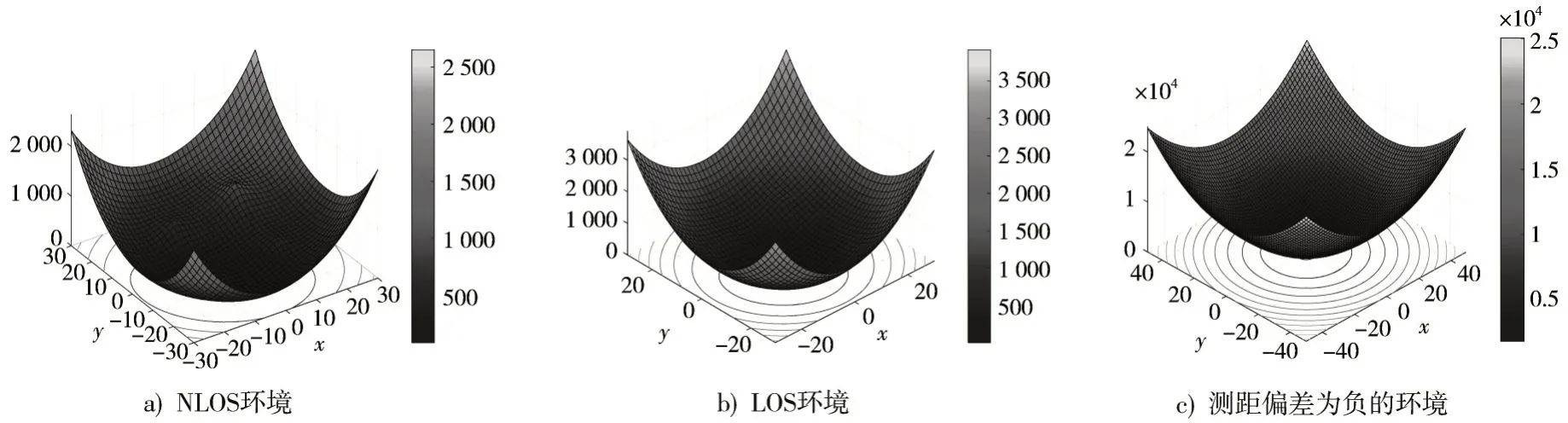
图1 非协同各场景代价函数
图2分别显示了二维平面中各个点Hessian矩阵的半正定情况,其中红色部分表示≽0,蓝色部分表示≼0,绿色部分表示不定。

图2 非协同各场景Hessian矩阵正定图像
由定理1可知,当为半正定时,函数为凸。从图2a)中可以看出,当定位环境为NLOS环境时,的半正定区域不连续,不定与半负定面积总和较大,当定位环境为LOS环境时,的半正定区域连续,不定与半负定面积总和较小。由命题2可知,当存在正的测距误差时,则代价函数F在全局范围内为非凸,因此在上述的两个定位环境中,F在全局范围内均为非凸,如图1a)和图1b)所示。当测距误差为负且绝对值较大时,满足命题2中代价函数F为凸的全局条件,如图1c)和图2c)所示,由的半正定性和F函数图像可以看出,在全局范围内半正定且F在全局范围内为凸函数。
为了说明初值选取对迭代结果的影响,从各个方向选取不同的初值,用高斯-牛顿迭代法进行位置解算。解算结果如图3所示,其中虚线构成的圆表示测距半径为负,其大小为距离观测值的绝对值。从仿真结果可知,在NLOS环境中,LS代价函数F为非凸函数,存在多个极值点,当初始值不同时迭代算法会收敛到不同的极小值点;在LOS环境中测距偏差较小,LS代价函数在全局范围内为非凸,但其极值点个数并没有增加,在这种情况下迭代算法会收敛于同一个位置,说明LS模型在LOS场景中适用;在偏差为负的场景中,迭代结果与初始位置无关,验证了在此情况下F具有全局收敛的特性。

图3 非协同各场景仿真迭代结果
在协同场景中,选取不同的初值,利用高斯-牛顿迭代算法解算用户位置,仿真结果分别如图4所示。在NLOS定位环境中,由于存在较大的正测距误差,使得F在全局范围内非凸并且导致产生了多个极值点,因此不同的初始值会导致算法迭代收敛到不同的极值点上;在LOS定位环境中,F在全局范围内为非凸,但正测距偏差较小,因此仍然可以收敛到相同的极值点上;在测距偏差为负的情况下,F在全局范围内为凸,因此无论初值如何选取,其必然会收敛到全局最优解。此结果较好地验证了命题2的正确性。
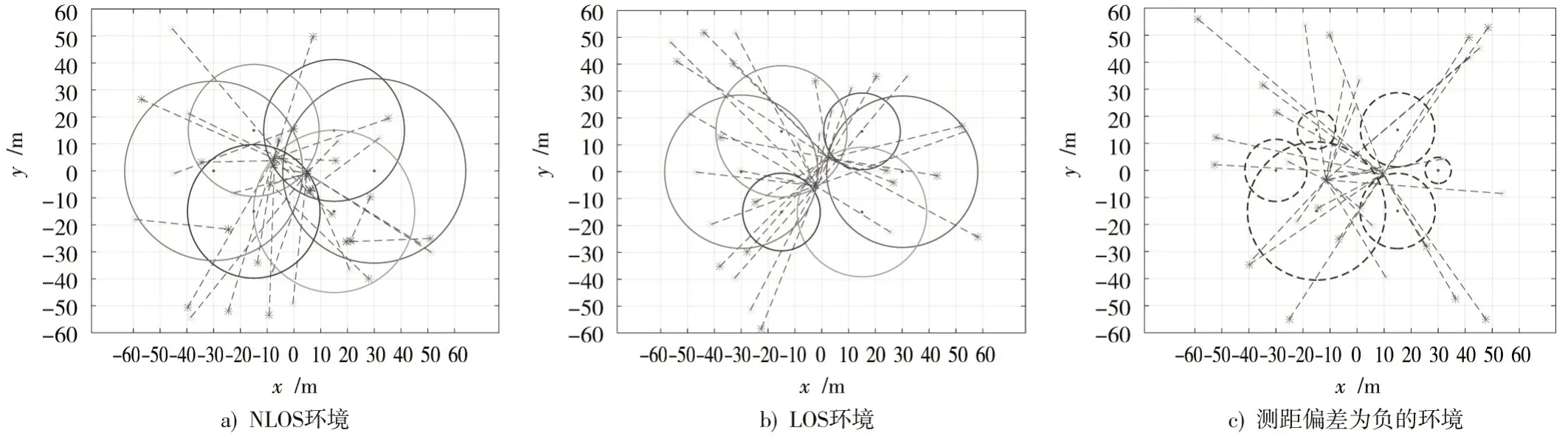
图4 协同各场景仿真迭代结果
4 结语
本文对协同定位无约束LS定位模型进行了凸性分析。通过对代价函数的Hessian矩阵的分析,得出了无约束LS代价函数的一个充分不必要条件,该条件指出,当测距偏差全部为负时,无约束LS定位代价函数全局为凸。在此基础上,分别对NLOS环境、LOS环境以及测距偏差为负环境下的LS代价函数凸性进行了仿真分析,验证了该命题的正确性。除此以外,本文提出影响最小二乘代价函数非凸性的主要因素为正测距偏差,为后续研究奠定了理论基础。
