基于BP神经网络水库水质模拟预测

孟朝霞，蒋 芃，贾宏恩

(1. 山西能源学院 能源与动力工程系；2.太原理工大学 数学学院，太原 036500)

1. 引言

相关部门对我国重点城市的饮用水水源型水库进行监察和检测的结果表明，水源型水库水质达标率不到80%，其中近24%的水库水质无法满足Ⅲ类水标准[1]。鉴于此，作为居民饮用水主要来源的水库水质问题，亟待解决。

现有的水质预测方法均通过相关预测手段，利用水质监测历史数据，推导求取水库各指标与待测指标之间的非线性关系，或是通过研究某个水质指标的时间序列，从中找到水质变化的规律，来预测未来水质的变化情况。根据水质预测理论基础不同，目前常用的水质预测方法主要有5类，分别为：数理统计法、灰色模型预测法、神经网络模型预测法、水质模拟模型法、混沌理论预测法等[2]。

在数理统计的方法中，应用于水质预测的回归分析方法效果较好。但也存在一些问题，如：计算量大、适应性差以及只重拟合不重外推等[3]。而灰色模型预测可以弥补回归分析不中外推缺陷，根据单因素趋势外推进行水质预测[4]。随着近年来神经网络的不断发展，已经有相关学者对河流中影响水质的指标建立模型，并取得了不错的预测效果[5-7]。混沌理论预测法着力于“由繁化简”，将复杂的多重耦合多变量关系转变为单一单变量关系，从系统总体出发，研究复杂体系的内在发展规律，并以混沌空间模线性回归模型预测河流水质系统的短期发展变化趋势[8]。在建立水质预测模型时应多方面考虑水质历史数据，选取恰当的预测手段。

本次研究的水库主体，位于中国中部地区，属黄河水系。其总面积为32.0平方公里，水库平均深度为6.5米，其中最大深度为19.0米，属于淤泥底质。其控制的流域面积为5268.0平方公里，水库容量7.0亿立方米，预计灌溉面积为149.2万亩。该水库的水质安全与当地人民的生活质量息息相关，本文选取BP神经网络建立模型，对目标水库数据进行建模分析，预测未来水库水质质量。

2. BPNN模型参数预处理

通过BP神经网络算法，构建基于BP神经网络的水库健康预测模型，实现对评价水库健康指标的预测，并根据预测值判断水库水质健康状态。

2.1 神经网络拓扑结构

本模型神经网络拓扑结构如图1所示，分为输入层、隐含层以及输出层[9]。本文采用具有多个输入神经元、一个输出神经元且具有双隐含层的反向传播拓扑结构建立神经网络。

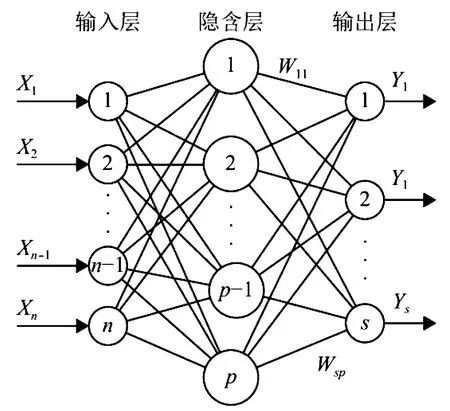
图1 神经网络拓扑结构

选取水库2018—2020年内共35个月的水库健康指标，根据特征指标的相关性分析，决定每种预测指标的输入神经元个数。根据预测误差最小化原则分别测试50-150个隐含层神经元个数，选择每种预测指标模型的最优隐含层个数[10]。输出层神经元个数为1。

2.2 样本数据

为达到模型最佳的泛化程度，本文利用已有水库指标数据集对模型中BP神经网络部分进行初始权重参数的调整以及神经网络拓扑结构的训练。建立模型之后，需要将数据集进行划分，验证模型的泛化能力以及模型对水库水质预测能力。因此，本模型将数据的20%作为测试集、80%作为训练集，不断完善本模型BPNN部分的神经网络拓扑结构[11]。

2.3 数据处理

针对本模型需要预测的水质指标，本文使用Spearman等级相关系数对数据所给特征进行相关性分析，以此找出各个特征之间的相关性关系。

为防止小量纲数据被大量纲数据被淹没，神经网络在训练模型之前，都会对数据进行归一化处理，以解决所分析数据之间的可比性问题[13]。模型将原始数据的量纲进行归一化处理后，更有利于训练出适用于运势数据的合适的神经网络模型，从而解决问题。

由于水库所提供的相关水库健康指标数据量纲不同，故在进行训练之前需要数据归一化处理。本模型采用min-max标准化数据归一化的方法，处理指令如下：

x_scaler=MinMaxScaler(feature_range=(-1,1))

y_scaler=MinMaxScaler(feature_range=(-1,1))

2.4 模型训练

面对已经获得的没有线性关系的数据，我们选择具有较好自适应能力和记忆功能的BP神经网络模型来解决实际问题[14]。BP神经网络采用的学习方法为最速下降法，数据经过正向传播后再经过反向传播不断调整神经节点之间的权重(权值)和偏置(阈值)，从而得到网络的最小误差平方和。BPNN模型拓扑结构训练其本质上为优化问题，通过优化找到满足条件的最小误差。

为保证BPNN模型的预测精度，本文利用PYCHARM软件编程建立双隐含层BP神经网络，采用sklearn中MLPRegressor函数建立回归模型，以观测值与预测值之间的均方误差(mean squared error，MSE)作为神经网络模型的预测性能函数，以此作为训练的一部分对BPNN模型纠正，以实现对水库水质指数变化规律的预测。

3. 基于BP神经网络水库水质模拟预测方法

根据数据所给特征，将所有特征均作为预测水质指标的因变量是不恰当的，相关性不高的特征组合会对模型预测结果造成过拟合影响。在训练模型之前进行相关性分析，计算每两个特征之间相关系数并找出与各水质预测指标相关性较大的特征组合。本文将Spearman等级相关系数引入BPNN模型中，优化特征组合，防止模型过拟合现象，进而提高CORR-BPNN模型的拟合程度，提高模型预测精度。

3.1 相关性分析

为寻找预测目标与其余特征之间的相互关系，模型更好拟合，我们引用Spearman等级相关系数。两个变量的相关系数绝对值越接近1，两变量之间相关性越强，相关系数与相关程度如表1所示。

表1 |r|的取值与相关程度

计算相关系数公式如下：

(1)

其中d为X和Y之间的等级差。通过PYCHARM程序编写，计算特征之间的Spearman等级相关系数，找到预测目标相关性较好的特征组合。

3.2 性能分析

本文构造CORR-BPMM水库水质模型，其预测准确性采取均方根误差(RMSE)、平均绝对误差(MAE)和平均相对误差(MRE)进行评价。公式如下：

(2)

(3)

(4)

3.3 计算流程

本文构建BPNN水库水质预测模型，实现对水库水质的预测预警。对于未知分布规律的数据，在构建BPNN模型之前，本文通过PYCHARM编写程序计算Spearman上等级相关系数，可视化相关系数热力分析图。

各BPNN模型中输入神经元个数由等级相关系数决定，输出层神经元个数均为1，输出数据即为水质指标预测值。未来可根据规划指标值预测水库监管指标的指标值。BPNN模型具体计算流程如图2所示。

图2 BPNN模型计算流程

(1)根据所给数据，采用Spearman计算各特征之间的等级相关系数，计算过程如下：

首先对两个变量(X，Y)的数据进行排序，记排序以后的数据位置为(X′，Y′)，(X′，Y′)的值就成为秩次，秩次的差值为公式(1)中的di，n为变量中数据的个数，根据公式计算最终得到Spearman等级相关系数。具体操作由PYCHARM编程实现，并生成相关系数热力图。

(2)建立BPNN模型的参数设定如下，模型采用SKlearn中的MLPRegressor模型，BPNN模型一程序表达式为：

隐含层每层节点数为100，110：hidden_layer_sizes=(100,110)

激活函数：activation='relu'

权重优化算法：solver='lbfgs'

正则化项系数：alpha=0.0001

学习率：learning_rate='constant'，learning_rate_init=0.001

迭代次数：max_iter=25000

优化算法停止条件：tol=1e-4；

(3)BPNN模型二程序表达式为：

隐含层每层节点数为100，110：hidden_layer_sizes=(100,110)

激活函数：activation='relu'

权重优化算法：solver='lbfgs'

正则化项系数：alpha=0.0001

学习率：learning_rate='constant'，learning_rate_init=0.001

迭代次数：max_iter=200

优化算法停止条件：tol=1e-4；

(4)BPNN模型三程序表达式为：

隐含层每层节点数为100，100：hidden_layer_sizes=(100,100)

激活函数：activation='relu'

权重优化算法：solver='lbfgs'

正则化项系数：alpha=0.0001

学习率：learning_rate='constant'，learning_rate_init=0.001

迭代次数：max_iter=200

优化算法停止条件：tol=1e-4

(5)利用BPNN神经网络算法拟合每一个预测指标模型的神经网络拓扑结构中的权值参数，到达预测值与观测值之间的最小误差。

(6)输出各模型预测结果

4. 数值结果

BPNN水库水质预测模型包括两个阶段：计算各特征之间的相关性系数，决定各预测指标特征变量；建立各预测指标的BP神经网络，训练并拟合BP神经网络拓扑结构，输出预测指标值,从而完成水质指标预测任务。

4.1 相关系数计算结果

本文将山西某水库所给数据带入Spearman等级相关系数模型，计算相关系数，计算结果如图3所示。

图3 各特征指标相关系数热力图

根据相关系数确定溶解氧、五日生化需氧量、气温相关性系数均>0.5，具有中高度相关性；总磷、水位、氯化物、电导率相关性系数>0.5，具有中高度相关性；总硬度、硝酸盐、电导率、叶绿素相关性系数均>0.5，具有中高度相关性。故我们以溶解氧、总磷、总硬度作为水质预测的三个指标，分别建立BPNN模型一、二、三。

4.2 BPNN水库水质预测结果

将数据标准化后，按照80%、20%的比例划分数据，建立训练集以及测试集用于测试、训练拟合BPNN网络拓扑结构。

当神经网络各隐含层神经元个数为100、110时，模型的拟合效果较好，精确度较高，模型预测性能良好，BPNN模型对水质指标溶解氧的预测值与观测值走势如图4所示。

图4 溶解氧预测值与观测值走势图

当神经网络各隐含层神经元个数为100、110时，模型的拟合效果较好，精确度较高，模型预测性能良好，BPNN模型对水质指标总磷的预测值与观测值走势如图5所示。

图5 总磷预测值与观测值走势图

当神经网络各隐含层神经元个数为100、100时，模型的拟合效果较好，精确度较高，模型预测性能良好，BPNN模型对水质指标总硬度的预测值与观测值走势如图6所示。

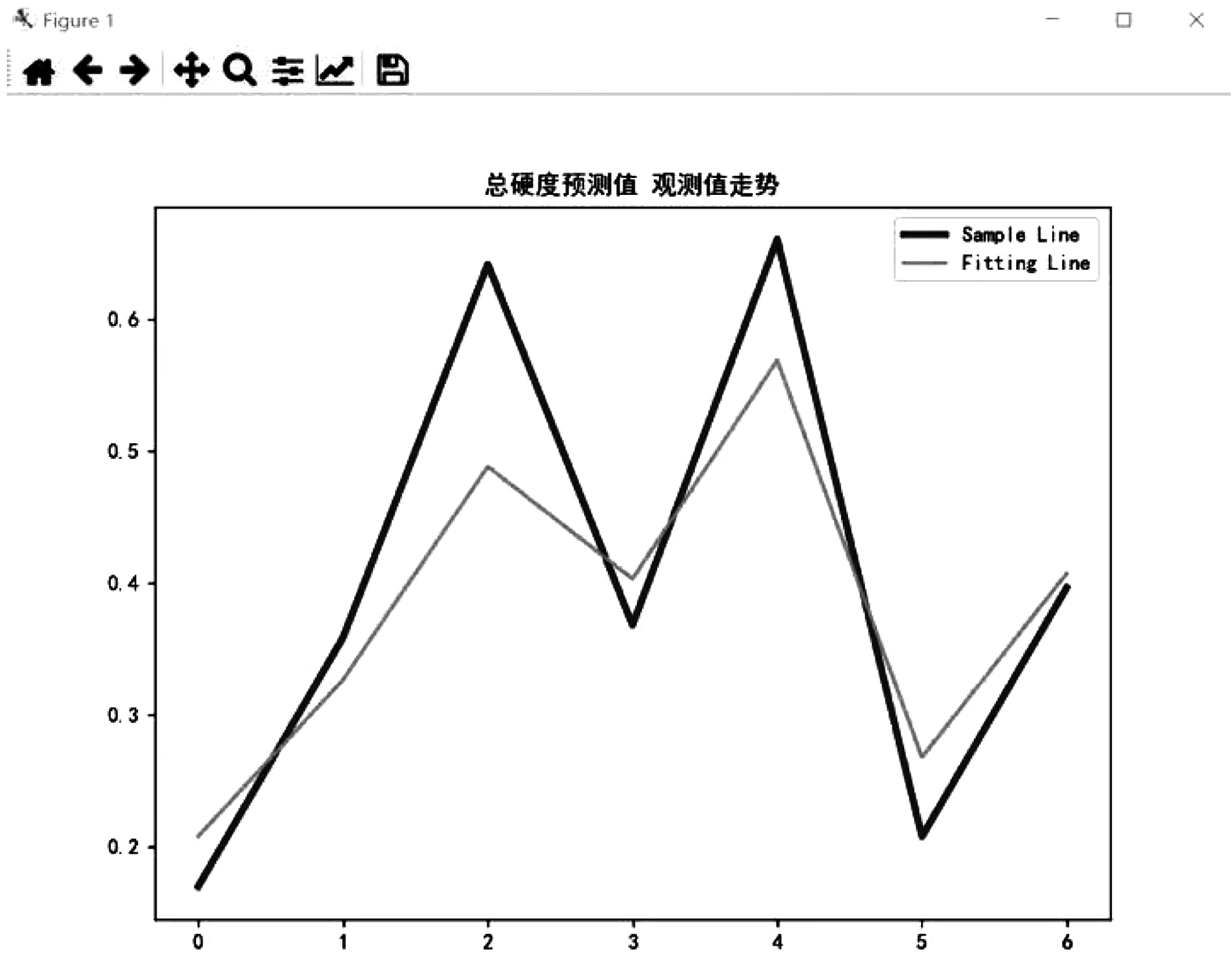
图6 总硬度预测值与观测值走势图

由图3-图5可知，本文构建的BPNN模型对与水质指标(溶解氧、总磷、总硬度)的预测值与观测值的重合度是较高的，各指标的发展趋势与走向也基本一致，但偶有偏差，BPNN模型对水库各水质指标的预测较为理想。

4.3 性能分析

本文采用3种评价指标来评定BPNN模型效能，分别为：RMSE、MAE和MRE。BPNN水质预测模型预测结果的误差分析见表2。

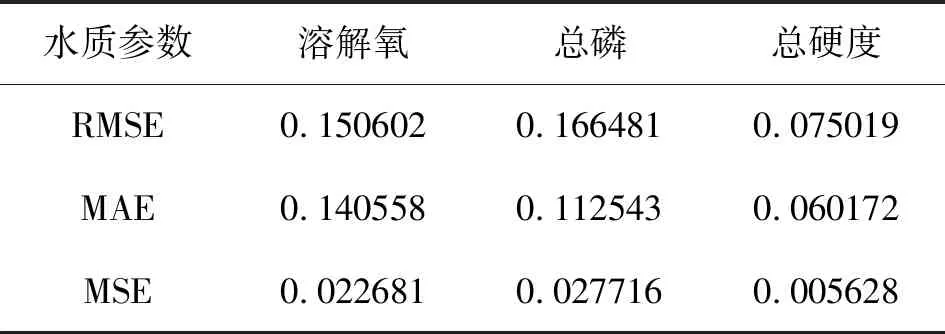
表2 BPNN模型预测结果误差分析

由表2可知，溶解氧、总磷预测值的RMSE值均小于0.17，总硬度预测值的RMSE值小于0.08；溶解氧、总磷预测值的MAE值均小于0.15，总硬度预测值的MAE值小于0.07；溶解氧、总磷预测值的MSE值均小于0.03，总硬度预测值的MSE值小于0.006。3项评价指标参数RMSE、MAE、MSE的计算结果均表明本文构建的BPNN模型对于水库各预测指标的预测结果均是理想的，是符合水质预测的要求，可以对山西某水库水质进行有效预测。

5 结果与展望

本文通过山西某水库2018—2020年的水质指标建立水质评价模型，选取3个指标建立BPNN模型。三个BPNN模型输入层神经元个数均为三个，输出层神经元个数均为一个，建立隐含层为两层的BP神经网络模型，对水质指标进行预测。经过数据验证，模型结果良好、预测结果与真实值的相对误差也在允许的范围内且可以作为较为精确的预测结果进行未来的水质预警工作。出于让模型精度更高的目的考虑，建议在后期使用该模型时，增加训练数据，以提高模型精度。相比于BP神经网络无法预测水质变化原因的缺点来看，其预测精度高、模型建立简单、适应性强的优点已经足够专业人员为未来干预水库水质做出策略。受数据可获取性限制，本文预测指标只考虑了溶解氧、总磷、总硬度指标，关于水库健康预警模型还需日后数据更加完善时加以研究。