浙江工业增加值增长预测研究
——基于ARMAX 和神经网络混合模型的实证检验
2022-02-15杨士鹏姜玮陈珍珍
□杨士鹏 姜玮 陈珍珍
工业是立国之本、强国之基。浙江作为工业强省,2021 年规模以上工业增加值首次突破2 万亿元,工业增加值占GDP 比重达到36.7%。尽管近年来浙江工业经济发展总体上取得了巨大成就,但同时也面临着增速放缓、资源趋紧、动能转换等新情况、新特点。尤其是今年以来,面对新冠肺炎疫情多发散发和俄乌冲突等超预期因素的影响,工业经济发展面临的不确定性加大。本文在全面探索应用时间序列、神经网络等单一模型进行预测分析的基础上,构建混合模型对工业增加值增长情况进行测度,期望得到满意的预测结果。
|主要变量指标选取及数据预处理
(一)主要变量指标选取
影响工业增加值增长(IDV)的因素很多,本文结合前人研究成果,首先将“克强指数”中影响工业经济发展的三个重要指标工业用电量(IDE)、货运量(TRANS)、中长期贷款余额(LOAN) 等率先纳入研究范围,同时引入宏观经济指标中影响较大的工业投资(IDI)、社会消费品零售总额(TOC)、出口总额(EXP0)、生产者价格指数(PPI)等指标作为补充。为了充分体现工业增加值增长预测的时效性,选取工业增加值增长和各个自变量的月度指标增长数据构建模型。
(二)变量数据序列的描述及初步处理
1.月度时间序列的收集。选取2015 年2 月至2022 年4 月的月度数据进行分析,由于工业、投资等统计月报免报造成1 月份数据缺失,故最终每个变量共有80 个数据。在模型构建并预测时,采用前面77 个数据进行模型构建,后面三期数据进行预测检验。
2.对各变量数据统一量纲。将所有指标转化为同比累计增长速度。各研究指标采取同比增长速度可在一定程度上剔除由于日历效应等引起的季节因素的影响,从而真实反映经济时间序列变动的客观规律。
(三)关键影响变量的初步筛选
首先利用Lasso 方法进行变量选取,一方面可以解决多重共线性问题,另一方面可以将跟工业增加值没有关联的指标舍弃。经初步筛选,将工业用电量、工业投资、社会消费品零售总额、货运量、中长期贷款余额、PPI 等自变量指标作为研究变量。
|基于ARMA 和ARMAX 模型的工业增加值增长预测
(一)时间序列模型简介
传统时间序列模型的构建基础为变量序列具有平稳性特征。平稳的时间序列可利用ARMA 模型进行直接建模,但如果序列有明显非平稳特性,则需进一步分析判断,可以尝试建立ARIMA 模型,即需要对非平稳序列经过适当差分转变成平稳序列后再建模分析。
1.ARMA 模型。自回归移动平均ARMA (p,q) 模型的结构如下:
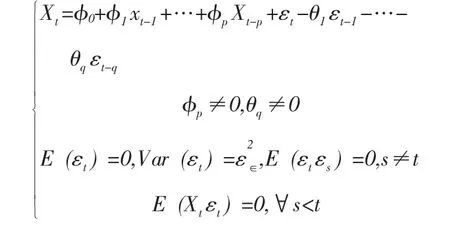
通常将模型ARMA(p,q)简记为:
2.ARIMA模型。AR、MA、ARMA 等上述三种模型都是适用于平稳序列建模。对于非平稳序列可以构建差分自回归移动平均模型,也就是ARIMA 模型。ARIMA (p,d,q) 模型的结构如下:
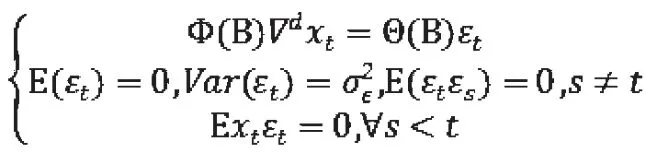
可以将上述模型简记为:
3.ARIMAX 模型。假定响应序列 {yt} 与输入变量序列 {x1t},{x2t},…,{xkt} 都是平稳的,构建响应序列和输入变量的回归模型:
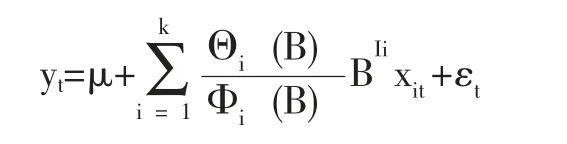
因为 {yt} 与输入变量序列{x1t},{x2t},…,{xkt} 均为平稳序列,故平稳序列的线性组合仍具有平稳性,模型拟合得到的残差序列{εt}同样也是平稳的,这就可以利用ARMA 模型继续提取残差序列中{εt} 的有用信息。得到的最终模型为:
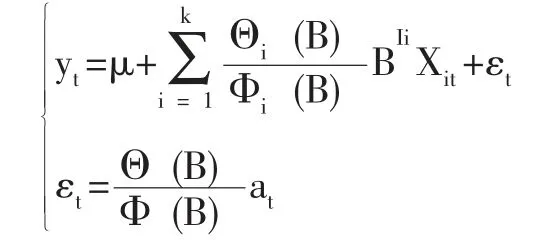
上述动态自回归移动回归模型即为ARIMAX 模型。其中Φ (B)表示为残差序列自回归系数多项式;Θ (B) 为残差序列移动平均系数多项式;at是零均值白噪声序列。
(二)变量序列的平稳性检验
通常可以采用各变量序列的时序图、ADF 检验等方法判断变量序列是否平稳。从IDV、IDE 等指标序列时序图可以初步看出,除了LOAN、PPI 显示出较强的非平稳性特征外,IDV、IDE 等其他五个指标时序图均显示出了平稳性特征。变量IDV、IDE、IDI、TOC、TRANS 等多数序列通过5%的ADF检验,表明序列是平稳的。而LOAN和PPI序列的ADF检验t统计量的值,大于显著性水平为5%的临界值,表明序列为非平稳的,与利用时序图得到的结论一致。
(三)ARMA 模型预测
1.模型的适用检验及阶数初定。通常通过ACF 和PACF 相关图可以识别ARMA 模型的阶数。根据本文研究变量的相关图特征,根据经验可以初步对IDV 序列构建ARMA(2,1)、ARMA (2,0)、ARMA (1,1)、ARMA (1,0) 等形式的模型。从本研究的价值角度看,是找到适用的预测模型,为判断工业经济增长服务。故选择拟合优度最大的模型来作为本文的预测模型。结果表明,ARMA (2,1) 的预测结果也比其他三种模型的相对误差小。
2.ARMA(2,1)模型形式及检验。使用最小二乘法进行参数的估计,得到工业增加值增长的预测模型(图1)。从预测模型的Inverted AR Roots 和Inverted MA Roots 等指标参数均小于1,说明模型是平稳的。通过对构建模型的残差序列进行检验可以看出,残差序列的自相关以及偏自相关系数都比较小,意味着残差序列为白噪声序列,即上述模型已充分提取了原始变量序列的信息,ARMA(2,1)模型形式见图1。

图1 ARMA(2,1)模型的构建结果
3.ARMA(2,1)模型预测结果。利用构建的ARMA (2,1) 模型对2022 年1-2 月、1-3 月、1-4 月等时期的累计增长速度进行预测(表1)。
由表1 可知,ARMA (2,1) 模型短期内的预测值比长期明显要好,随着时间变动,预测值与真实值的相对误差出现增大迹象。总的说来,ARMA 模型预测的总体结果并不能令人满意。

表1 浙江工业增加值预测值与真实值对比 (单位:%)
(四)ARMAX 模型预测
前面分析已知,IDV、IDE、IDI、TOC、TRANS等时间序列变量均表现为平稳性特征,初步判断适合建立ARMAX 类模型进行预测分析。而LOAN 由于为非平稳时间序列,本文将对其不作为工业增加值增长影响因素进行建模。
1.IDV 和 IDE、IDI、TOC、TRANS 等变量的协整检验。建立多元动态回归模型即ARMAX 模型,为避免出现虚假回归问题,要先对IDV和IDE、IDI、TOC、TRANS等之间的关系进行协整检验,从检验结果的最大特征值和迹特征值可以判断出IDV 和IDE、IDI、TOC、TRANS等变量序列之间具有协整关系,故可以建立多元动态回归模型而不用担心虚假回归等问题。
2.IDV序列与IDE、IDI等序列的协相关检验。IDV与IDE、IDI等拟研究变量走势基本相同,从IDV 和IDE 的协相关图可知,IDV与IDE 序列存在着很强的相关性,并且随着延迟期数变小,相关性越大,在延迟阶数为零时,两者的协相关系数最大,也就是说工业增加值增长与同期的工业用电量增长的相关性最大,故IDV 与IDE 两个变量序列可以建立同期回归模型。同理,经分析得到IDV和IDI、TRANS、TOC等指标序列同样可以建立同期的模型。
3.ARMAX 模型的构建及检验。借鉴上部分构建的ARMA 模型,并充分分析各自变量序列的内在特征,尝试构建ARMAX(1,1)、ARMAX(1,0)、ARMAX(2,1)和ARMAX (2,0) 等形式的动态自回归移动平均模型。经反复试验,ARMAX (2,1) 工业增加值增长预测模型拟合优度最高,作为本文的适用模型进行分析预测。使用最小二乘法进行参数的估计,最终得到工业增加值增长的预测模型如图2 所示。检验预测模型的残差序列显示自相关和偏自相关系数均比较小,即残差序列表现为白噪声序列,已充分提取了原始序列的信息。从Inverted AR Roots 和Inverted MA Roots 的值均小于1 可知,所建模型是平稳可行的。
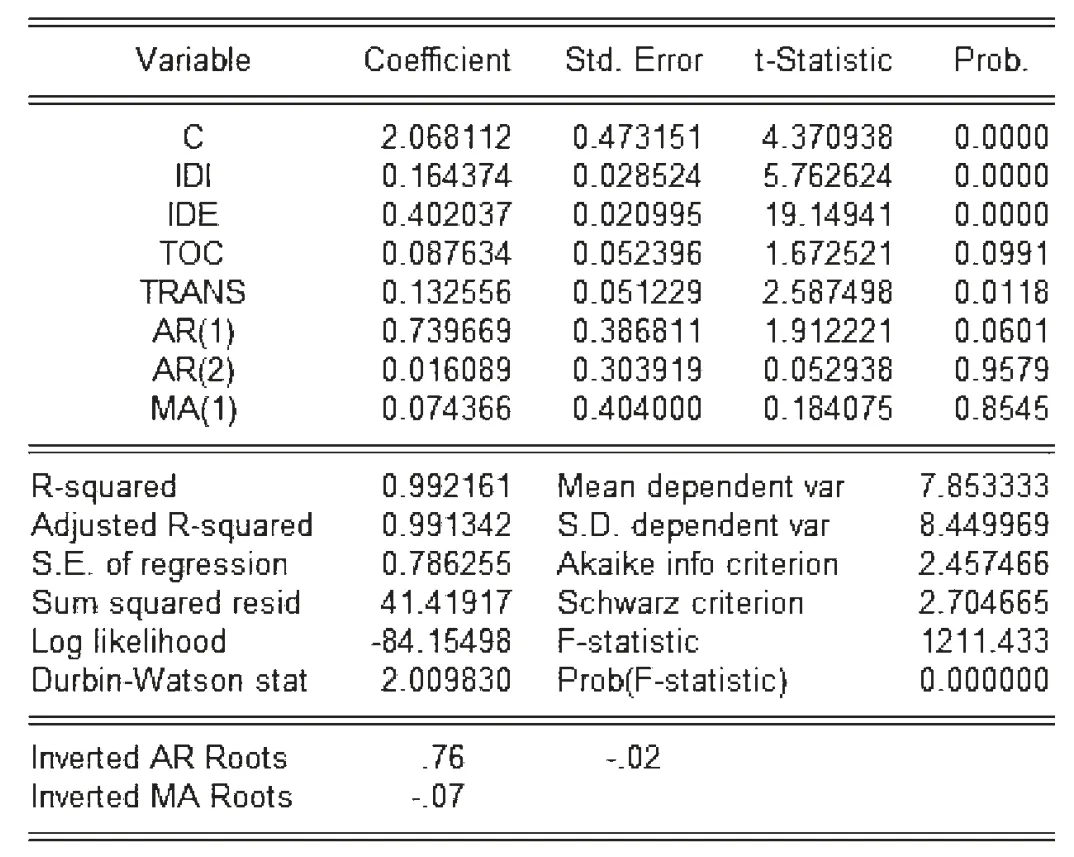
图2 ARMAX (2,1) 模型构建结果
4.ARMAX 模型的预测及分析。利用构建的ARMAX (2,1) 模型预测2022 年1-2 月、1-3月和1-4月的累计增长速度(表2)。结果表明,预测值的平均相对误差基本控制在5%以内,且短期内的预测值同样比长期更好。从总体上看,利用多元动态回归模型即ARMAX 模型对工业增加值增速进行预测效果较好。
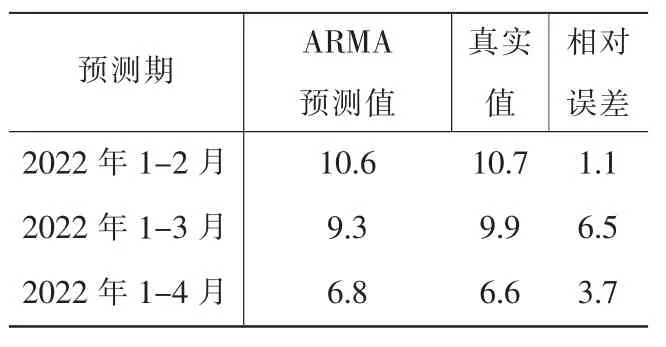
表2 基于ARMA (2,1) 工业增加值增速预测值与真实值对比(单位:%)
(五)ARMA 和ARMAX 模型的对比分析
总体上看,ARMAX 比ARMA模型的预测结果的相对误差有了明显降低,预测值更加准确,预测模型精度得到明显改善(表3)。但ARMAX 模型也存在预测时间越长精度越低的问题,这也是时间序列分析模型普遍存在的问题。
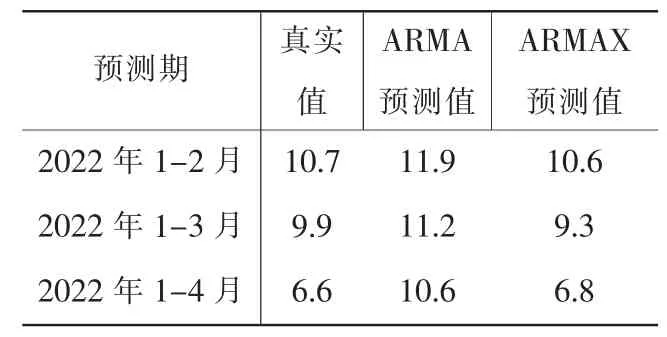
表3 工业增加值增速的ARMA 和ARMAX 预测值与真实值对比(单位:%)
|基于神经网络模型的工业增加值增长预测
(一)神经网络相关模型简介
1.神经网络介绍。目前,神经网络已成为有效解决各种复杂计算问题的最有吸引力的机器学习模型之一。从机器学习的角度看,神经网络作为一个高度非线性的数学模型,由大量具有非线性激活函数的神经元,借由一定的权重连接而成。神经网络中最基本成分是神经元模型,典型的神经元模型的基本结构如图3 所示。在该模型中,n个输入信号传入到神经元后通过带权重的连接在神经元内进行传递,之后全部的输入信号通过一个非线性的激活函数f(x)进行输出。
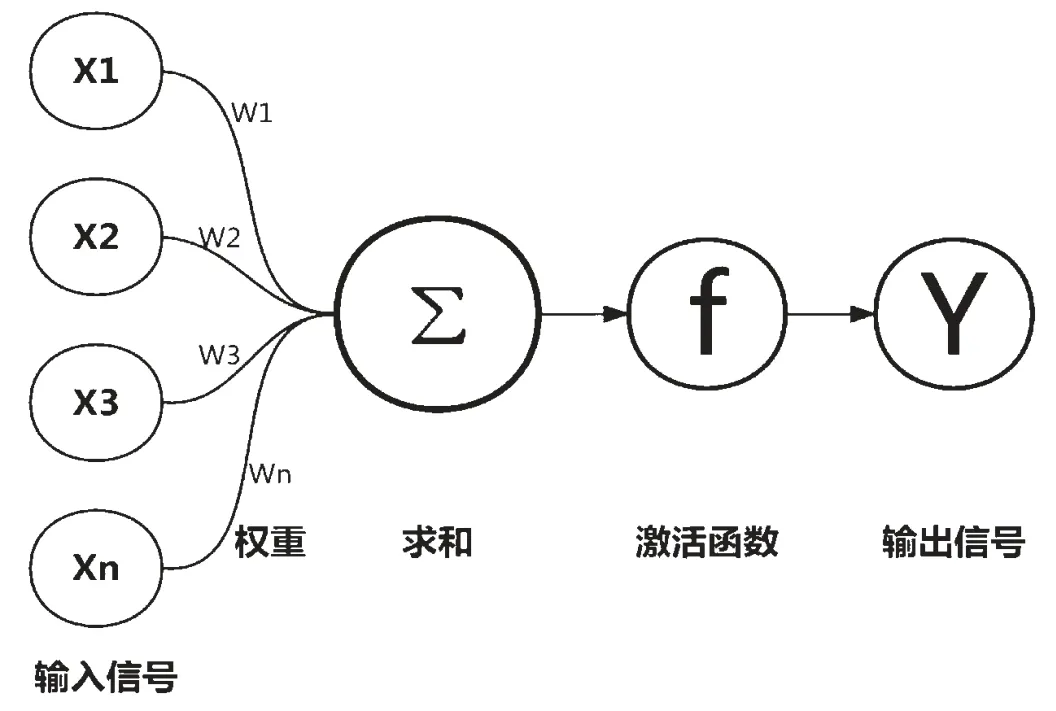
图3 典型的神经元模型
激活函数是获取输入信号并将其转换为输出信号的核心连接,神经网络中的激活函数包括线性函数、阶跃函数、Sigmoid 函数、双曲正切函数(tanh 函数)、线性修正单元函数(ReLU 函数)等。ReLU 函数因其具备生物学合理性、优化收敛速度快等优势,是目前深度神经网络中应用最广泛的激活函数。
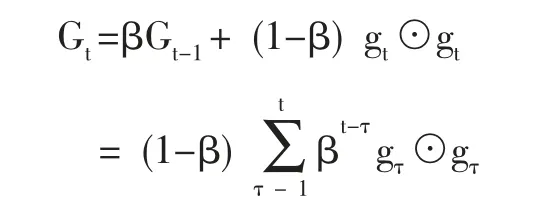
2.BP 神经网络。
(1)BP 神经网络。BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈神经网络,其拓扑结构包括输入层、隐含层和输出层,如图4 所示。BP神经网络的训练过程包括两个方面。一方面,信息通过隐含层神经元的激活函数从输入层传递到输出层;另一方面,通过比较输出值与实际值的误差,如果超出了预先确定的阈值,就反向传回误差信息,同时修正网络权值,直到输出值与实际值之间的误差在控制范围之内。
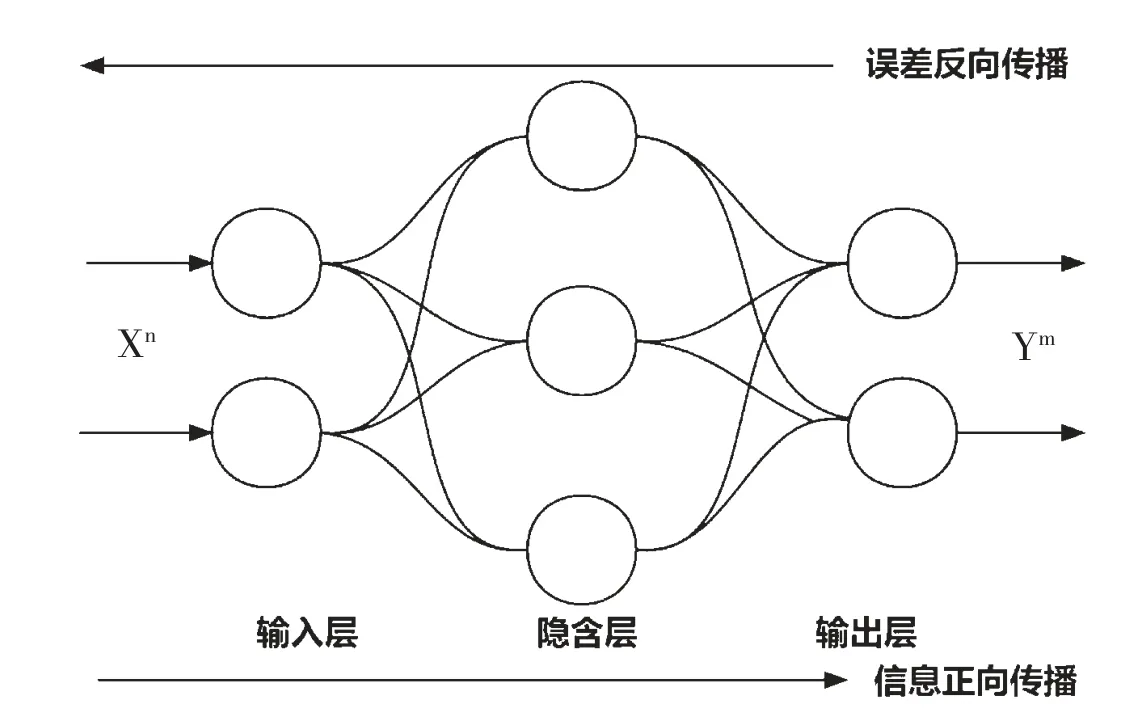
图4 BP 神经网络
(2)基于RMSprop 算法改进的BP 神经网络。经验表明,自适应学习率法中的 RMSprop 算法(Geoff Hinton,2012)能够克服AdaGrad 算法梯度急剧下降的问题,在很多应用中都展现出优秀的学习率自适应能力。RMSprop 算法结合梯度平方的指数衰减移动平均数来调节学习率的变化,其累计梯度平方的表达式为:
其中,β 为衰减率,一般取值为0.9。RMSprop 算法的参数更新值为:
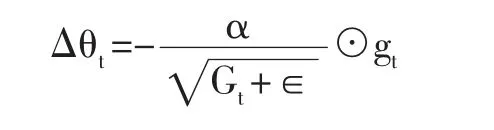
(二)数据变量指标的选取
建立基于RMSprop 算法改进的BP 神经网络模型,使用线性修正单元函数(ReLU 函数)作为激活函数。为确保模型结果的可比性,同样选取2015 年至2022 年4 月的浙江工业增加值增速作为因变量,工业用电量、出口总额、中长期贷款余额、货运量、工业投资、社会消费品零售总额和PPI 等7 个指标作为自变量。其中,以2015 年至2021 年共计77 组样本作为训练数据,以2022 年2 月至4 月共计3组样本作为测试数据。
(三)神经网络模型的构建
基于神经网络模型对77 组样本进行训练。随着迭代次数的不断增加,模型的均方根误差(RMSE)呈现断崖式下降,最终得到模型的均方根误差(RMSE)为0.902,判定系数(R2)为0.989,表明该模型对训练数据的解释程度较高。从模型的拟合曲线来看(图5),拟合曲线和45 度基准曲线(预测值等于实际值)基本吻合,表明模型的拟合效果较好。
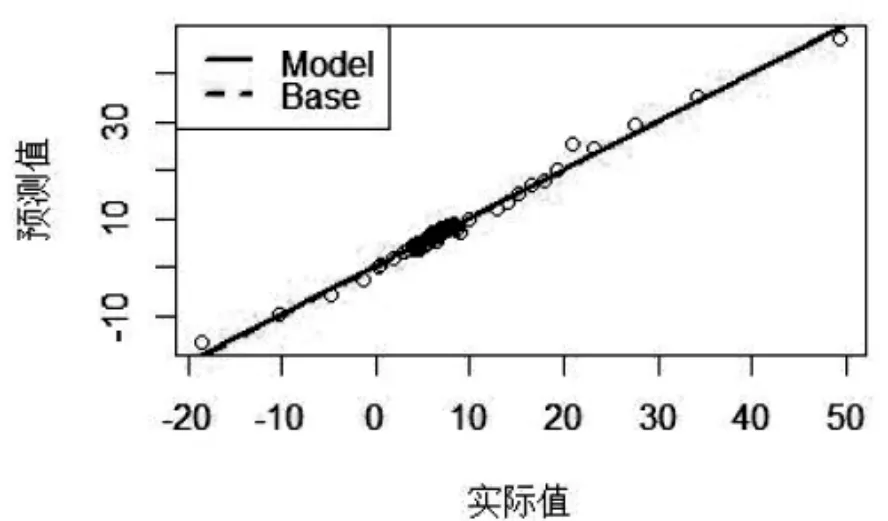
图5 神经网络实际值与预测值对比(训练集)
(四)神经网络模型预测
用训练好的神经网络模型对2022 年1-2 月、1-3 月和1-4 月的浙江省规模以上工业增加值增长速度进行预测,预测结果如表4 所示。
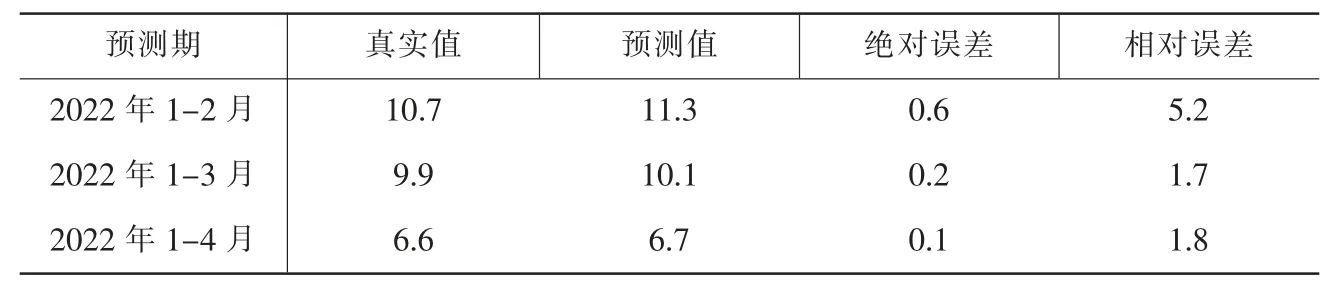
表4 神经网络模型预测结果(单位:%)
从表中可以看出,2022 年1-2月、1-3 月、1-4 月的预测相对误差分别为5.2%、1.7%和1.8%,预测值的平均相对误差为2.9%,均小于5%,表明预测效果较好,说明利用神经网络模型对工业增加值增速进行预测是切实可行的。
|基于混合模型的工业增加值增长预测
(一)混合模型简介
混合模型根据时间序列的特征,对多个单一模型进行有机结合,即充分利用了各个模型的优势,能够有效提高模型预测精度。因此,本文在全面考虑ARMAX 模型提取的序列线性特征和神经网络模型提取的非线性特征的基础上,结合工业增加值增长趋势受多种因素影响的实际,构建ARMAX-BP神经网络混合模型,以期提高模型的预测精度。
(二)ARMAX-BP 神经网络混合模型预测
基于ARMAX 模型,得到浙江工业增加值增速的拟合值和相应的残差数据。将2015 年4 月至2016年3 月的共计11 个ARMAX 模型拟合的残差数据作为第一组输入数据,2016 年4 月的残差数据作为预测值,按照这一模式生成67 组神经网络模型样本,其中,前64 组样本作为训练数据,后3 组样本作为测试数据。基于神经网络模型对64 组样本进行训练,得到模型的拟合曲线如图6 所示,表明模型的拟合效果较好。利用训练好的神经网络模型对2022 年1-2 月、1-3 月、1-4 月的工业增加值增速的残差项进行预测,预测值分别为-0.097、1.045 和-0.248。
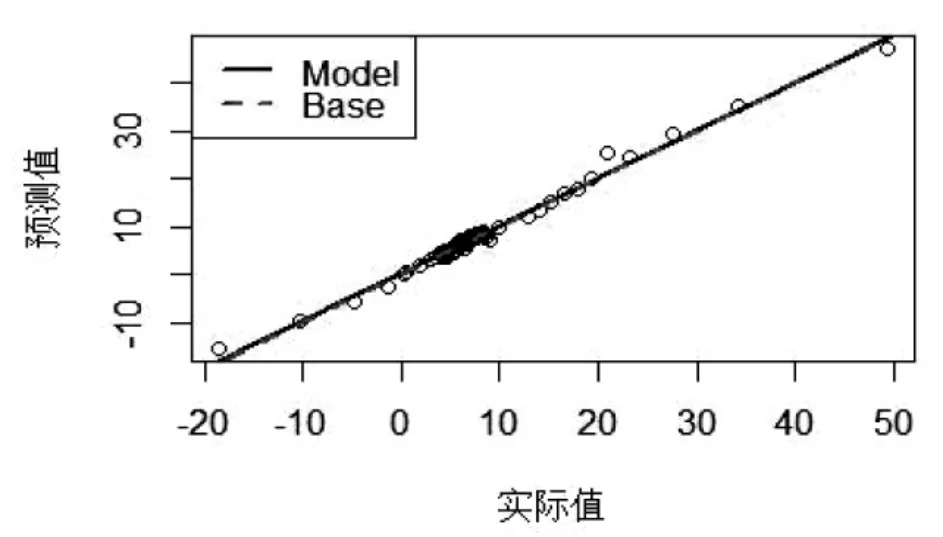
图6 神经网络实际值与预测值对比(训练集)
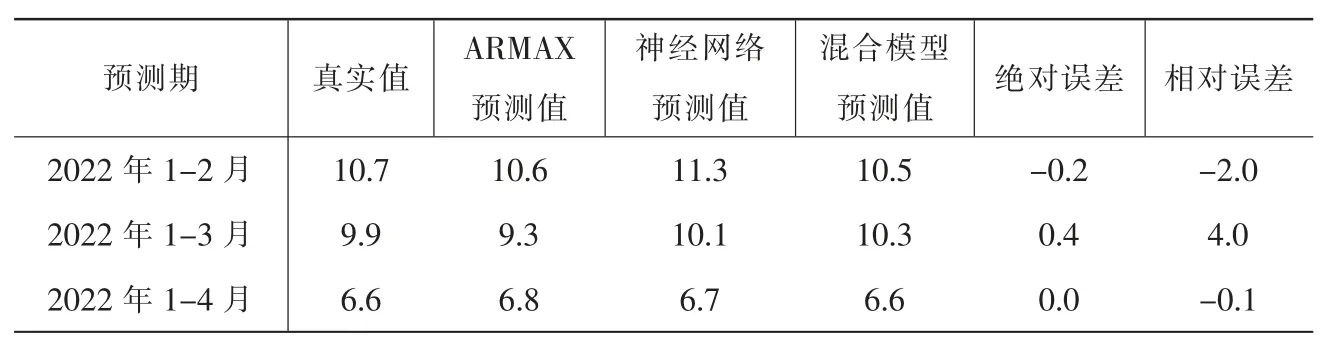
表5 ARMAX-BP 神经网络混合模型预测结果(单位:%)
(三)预测结果对比分析
将ARMAX 模型的工业增加值增长预测值和神经网络模型的残差项预测值相加,得到混合模型的预测值分别为10.5%、10.3%和6.6%,预测值的平均相对误差为2%。ARMAX-BP 神经网络混合模型的预测效果总体上优于各个单一模型预测效果,预测结果有了显著提升。
|结论与建议
(一)主要结论
本文在对有关预测理论模型回顾及评价的基础上,首先构建ARMA 模型和ARMAX 模型预测浙江工业增加值增长情况。预测结果显示,两类模型均能不同程度地短期预测工业增加值增长情况。将两个模型对比分析,发现加入影响变量的ARMAX 模型的AIC、BIC 值更小,预测结果也要显著好于ARMA 模型,即加入IDE、IDI、TOC、TRANS 等变量有助于预测工业增加值增长的发展趋势。
其次,构建基于RMSprop 算法改进的BP 神经网络模型对工业增加值增长进行预测,模型预测结果略好于ARMAX 模型的预测效果,这表明神经网络模型也可以实现对工业增加值增长的较好预测。
最后,构建ARMAX-BP 神经网络混合模型,尝试利用ARMAX模型充分挖掘工业增加值增长序列的线性特征,然后将ARMAX 模型的残差序列作为不含线性信息的部分,利用BP 神经网络模型充分挖掘其中蕴含的非线性信息,之后将线性部分和非线性部分的预测值相加,即可以得到混合模型的预测值。
通过对各种模型的预测结果进行对比分析,结果显示ARMAXBP 神经网络混合模型的预测结果优于各个单一模型,表明将传统时间序列和神经网络相结合的混合模型能够充分发挥各自优势,有效提高模型的预测精度。
(二)不足与建议
本文可利用的多变量建模的IDV、IDE、IDI 等时间序列数据仅有80 组,数据量总体还偏少,可能会在一定程度上降低预测精度,而BP 神经网络对用于训练的样本量需求更多。在采用相关模型进行预测分析时,本文着重从宏观层面探讨了省级层面工业增加值增长的变动趋势,如果将该研究方法推广到具体行业大类、设区市甚至区(县、市)等层面的趋势预测时,可能会出现预测结果精度下降的情况,有必要进一步优化模型构建,使用更多的样本数据对模型进行训练。
