基于改进的Focal Loss函数XGBoost的信用卡诈骗预测模型

王 威

（中国刑事警察学院 辽宁 沈阳 110000）

0 引言

随着信用卡在20世纪80年代从美国进入我国金融市场，我国信用卡发卡数量稳步上升[1]。在大数据时代，信用卡的普及和使用给群众带来了极大的生活便利，与此同时，各种诈骗活动也络绎不绝地出现，严重影响到了群众的经济生活。信用卡诈骗犯罪保持高发态势，并且由于新经济生态的发展，其在作案手段、流程、影响上有所升级，给公私财产造成了巨大损失。随着经侦“信息化建设，数据化实战”战略的稳步实施，犯罪预测已经成为当前公安经侦部门开展精准打击和有效治理的重要工具。通过数据分析研判、行为风险预警、犯罪形势预测对经济犯罪提前预警预判，掌握打击和治理经济犯罪的主动权。在经济犯罪发生之前，“靠前一步，主动作为”，及时预防和控制经济犯罪风险，尽可能减少和避免人民群众的财产损失，有力提高经济犯罪的侦破能力。因此，在现有公安数据资源的基础上，提出分析效率高、应用性能好的经济犯罪风险识别方法，对侦查工作具有重要的现实意义。

XGBoost算法作为机器学习算法中的佼佼者，自提出以来，已经在疾病预测、风险预测、异常检测以及其他领域方面都取得了非常优异的效果[2]。但是针对信用卡诈骗领域进行预测，由于数据集的不平衡性以及数据量的巨大，单一的XGBoost算法效果并不能令人满意。解决这一问题，一般是从数据和算法两个方面入手。其一是利用各种采样方法处理数据，解决数据集本身分布不均的现象；其二是对传统分类算法进行改进[3]。

基于此，针对信用卡诈骗领域数据集的不平衡性和庞大的数据量，本文提出一种利用损失函数（focal loss）改进XGBoost损失函数的信用卡诈骗预测模型，并使用评估指标来证明其具有良好的预测性能。利用损失函数来改进XGBoost中的损失函数，并用改进的分类算法训练新的数据集得到最终的预测模型。将本文模型和处理不平衡数据的分类模型做对比，结果表明本文提出的改进模型在信用卡诈骗预测中具有较好的分类效果。

1 XGBoost算法介绍

XGBoost算法是一种基于Boosting策略的集成学习算法。一般采用决策树作为其弱学习器，再通过特定的方法将多棵决策树进行整合，形成强学习器。其特点在于迭代，每迭代一次就生成一棵新的树。其采用梯度下降的思想，以之前生成的所有决策树为基础，向着最小化给定目标函数的方向进一步，并且能够自动利用CPU的多线程进行并行[4]。在处理不平衡数据方面，XGBoost算法具有相当优秀的性能。其主要公式如下：

模型定义为：

fk表示第K棵决策树，模型的目标函数定义为：

上式中，n为样本数，t为第t次迭代。第一项代表模型的损失函数，第二项代表抑制模型复杂性的正则项。

式（2）的第一项的二阶泰勒展开式为：

损失函数的一阶统计量为gi，二阶统计量为hi。具体计算如下：

式（2）的第二项可以展开简化为：

在第T次迭代中，由于t-1的树第一个结构已经确定，所以其复杂度之和可以用一个常数表示，将Ω（ft）定义为：

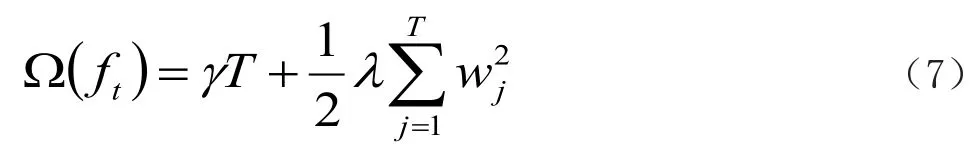
其中T为叶子节点数，为叶子节点向量权重的范例，第一项作为叶片数量的惩罚函数，第二项作为叶片节点权重的惩罚函数。

将式（3）和式（7）代入式（2），得到式（8）：

由二次方程的最优解公式可知，wj的最优解为

此时得到的最优目标函数值为

式（10）可以作为当前模型函数的评价分数，值越小表示模型表现越好。因此，当节点进行分割时，该分割的收益可由该公式得到：

GL、GR、HL、HR表示左右子节点样本集的一级统计和与左右子节点样本集的二级统计和。

通过上述公式，将XGBoost算法的过程总结如下：

步骤1：创建一个新的CART树。

步骤2：根据式（4）和式（5）计算每个样本的梯度统计量，开始迭代。

步骤3：根据贪心算法和梯度统计得到一棵新的树。

（1）：根据式（11）得到新树的最优分割点。

（2）：根据式（9）得到新书页子节点的权重值。

步骤4：将新树添加到模型中。

步骤5：迭代执行步骤1-步骤4，直到得到最终的模型。

2 基于改进损失函数的非平衡性XGBoost模型

在普通的 XGBoost模型中，梯度和海森矩阵的搜索是基于二进制交叉熵（lbce）的使用进行的，

在此使用加权的二元交叉熵损失函数（lwbce）和损失函数（lf）来代替二元交叉熵，从而解决数据不平衡的问题。

其中a是一个用来调整数据权重的不平衡参数，而γ是管理曲线形状的参数，其值越低，损失越高，反之亦然，是处理不平衡分类的重要部分[5]。

基于加权二元交叉熵的概念，这里提出了改进的损失函数（lMF）不平衡参数φ。该参数是由W-CEL函数的不平衡参数得到的。

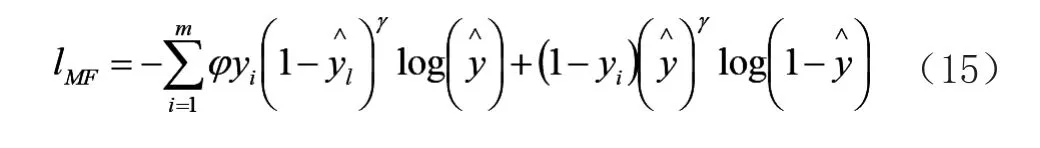
参数φ在式（15）中略有变化：

其中P代表正数类中的数据，N表示负数类中的数据，βi为二进制类的参数。

3 数据集准备

3.1 实验准备

为保证实验的严谨性，需要重点设置此次实验参数，具体如表1所示。

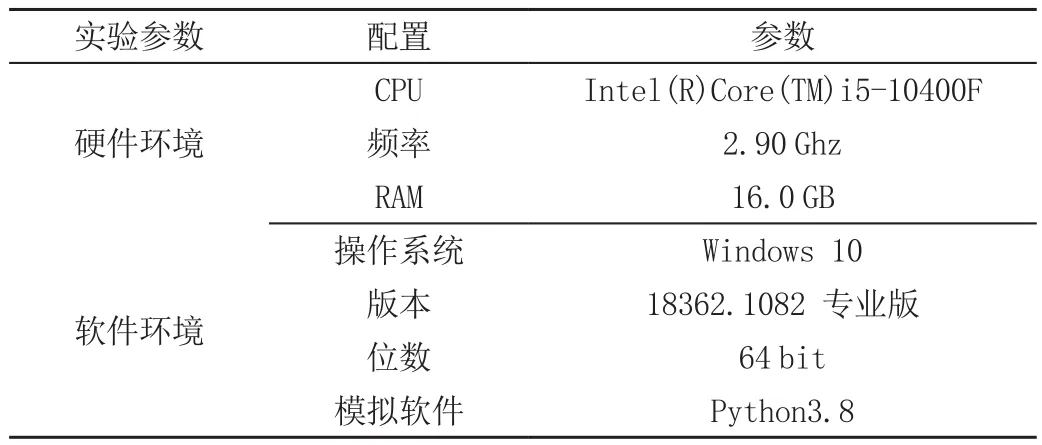
表1 实验参数

本文研究所用数据来源于Kaggle比赛中，Worldline和ULB的机器学习小组在进行大数据挖掘和欺诈检测的研究合作期间，提供的欧洲某信用卡公司在2013年9月的2天内的信用卡交易数据。该数据总共有284 807个样本，包含30个特征。但在全部284 807笔交易中只有492起诈骗行为，仅占全部交易的0.172%。数据相当不平衡，是典型的不平衡二分类样本。由于信用卡数据需要进行保密，故经过PCA特征提取后，全部特征中28个特征为V1，V2，V3…V28。而剩下的两个特征，TIME表示的是每笔交易与第一笔交易所相差的描述，单位为秒；另一个特征AMOUNT则为信用卡交易的金额。目标标签CLASS表示欺诈交易的是否，1表示是，0表示否[6]。

类不平衡数据中，正数类与负数类样本不成比例，由于数据的不规则分布，算法会偏向大多数的样本，可能导致分类的假阴性率高，算法对数据的处理效果不佳。从训练模型的角度来看，如果一类样本量过少，那么其提供的信息也会过少，模型无法学会如何区分少数类，如同极端情况：在1 000个训练样本中，999个为正，只有1个为负，那么在过程的某一次迭代结束时，模型将所有样本划分为正数类，尽管负数类被误分类，但是准确率仍有99.9%，损害可以忽略不计。因此，需要对数据进行预处理。

3.2 数据预处理

数据预处理是通过数据清洗和数据转换将不完整和不一致的真实数据转化为可处理的数据。对于任何的机器学习算法，数据质量都相当重要，因为这影响着分类器的性能。将不相关和冗余的特征进行剔除，可以提高模型的效率，减少模型的训练时间。在此采用min-max标准化方法进行归一，公式如下：

其中d`为归一化特征数据值，d为原始特征数据值，min（d）为所有数据的最小值，max（d）为所有数据的最大值。

在“数量”功能被规范化后，下一步是找到最相关的功能来使用。因此，为了找到每个特征的唯一性，使用相关系数来找到现有特征中最好的特征。

其中，F1是特征1，F2是特征2，F1F2是特征1和特征2的平均值。

3.3 使用性能指标进行模型评估

采用accuracy（准确率）、precision（精确率）、recall（召回值）、和MCC（马修斯相关系数）四个与不平衡分类相关的数据指标来评估模型的性能[7]。由于该数据集的数据偏向多数类，因此准确率的值会较高。在类不平衡模型中，只关注准确率可能会导致分类的极度不平衡。而精确度和召回率则因为提供了一致性，对评估提供了可靠的参考性。MCC因为包括了真阳性（TP）、假阴性（FN）、真阴性（TN）和假阳性（FP），非常适合用来评价不平衡的数据集。用0表示正数类即按时还款，1表示负数类即诈骗行为。其中TP（true positive）表示真实值为0，预测值也为0的样本数，FN（negative）表示真实值为0，预测值为1的样本数，FP（positive）表示真实值为1，预测值为0的样本数，TN（true negative）表示真实值为1，预测值也为1的样本数[8]。

下面定义用于度量分类器性能的度量标准：

准确率（accuracy）：在所有样本中模型预测正确的比例。

精确率（precision）：表示在模型预测为正数类的所有结果中，模型预测正确的比例。

召回率（recall）：表示在实际为正数类的所有结果中，模型预测正确的比例。

马修斯相关系数（MCC）：本质上是一个描述实际分类与预测分类之间的相关系数，它的取值范围为[-1,1]，取值为1时表示对受试对象的完美预测，取值为0时表示预测的结果还不如随机预测的结果，-1是指预测分类和实际分类完全不一致。

4 实验与结果

本实验通过三个不同的场景来进行，第一个场景使用原始数据，即正实例与负实例数量相差极多，极端失衡的情况。在第二个场景中，将原始数据最小化，这样正常交易类将有10 000个数据，但诈骗类的数据没有改变，即轻度失衡的情况。最后一个场景将正常交易类数据量提升至125 000个，其余不变。第一步执行“数量”特征的最小-最大标准化。第二步使用系数相关法进行特征选择。此外，实验将分为两部分，即不使用超参数进行传统机器学习的实验和使用超参数γ求值的实验。这两项实验都分为70%的训练集和30%的测试集。在表2中列出了场景1中几种传统的机器学习方法：逻辑回归（logistic regression）、支持向量机（support vector machine）、K近邻分布（k-nearest neighbour）和朴素贝叶斯（Naïve Bayes）。可以看出，由于数据分布是极度不平衡的，召回率和MCC值与准确度值相比有很大差异，而准确率都接近100%。

表2 场景1中传统机器学习算法的评估

表3是场景1中普通XGBoost、基于加权二元交叉熵损失函数的不平衡XGBoost、基于损失函数的不平衡XGBoost与FXGBoost的比较。在该表中，我们在XGBoost的t参数中不使用超参数进行调整，而是使用Scikit learn中的GridSearchCV方法来调整参数值γ和α。结果显示，FXGBoost模型的精确率高达0.97，与基于损失函数的不平衡XGBoost一致，是所有模型中最高的。并且FXGBoost的召回率为0.56，MCC值为0.72，都是所有模型中最高的。但是对于不平衡数据集来说，该模型表现仍不够优秀。为验证本文提出的模型在数据层面和算法层面的改进效果，我们将来自正常交易类数据的数量最小化，由284 315例减少为10 000例，称之为轻度失衡场景。同时创建了另一个场景将正常交易数据量减少为125 000个，称之为中度失衡场景。

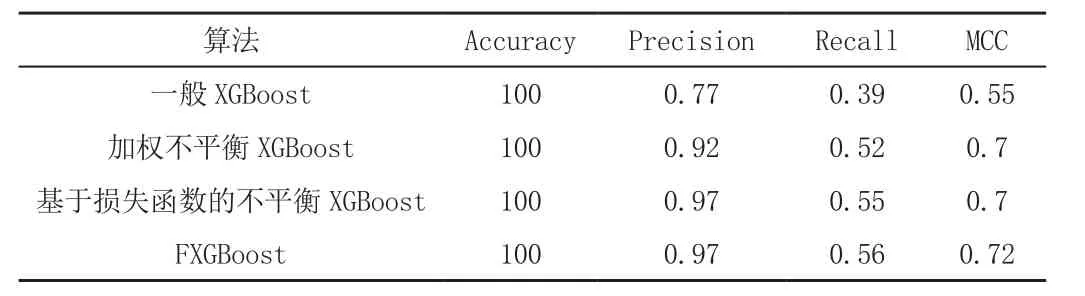
表3 场景1中各XGBoost算法的评估

表4列出了场景2中传统机器学习方法的评估结果。尽管这些模型显示的结果看起来很好，但是由于精确率、召回率和MCC的值相差很大，所以结果是无效的。表5列出了场景2中各方法的评估结果。结果显示，FXGBoost模型是其中最有效的，其精确度、召回率和MCC值相对接近，并且准确率与其他评估分数之间没有太大差距。基于损失函数的不平衡XGBoost方法虽然在精确度和召回率方面仍然存在差异，但在处理不平衡数据方面相对较好。表6是场景3中所有方法的评估结果，在场景3中，从MCC评分结果来看，FXGBoost是最好的方法。基于场景1和场景2中给出的实验，该方法比传统的机器学习以及不平衡XGBoost在处理不平衡数据集上的效果都要好。

表4 场景2中传统机器学习算法的评估

表5 场景2中各XGBoost算法的评估

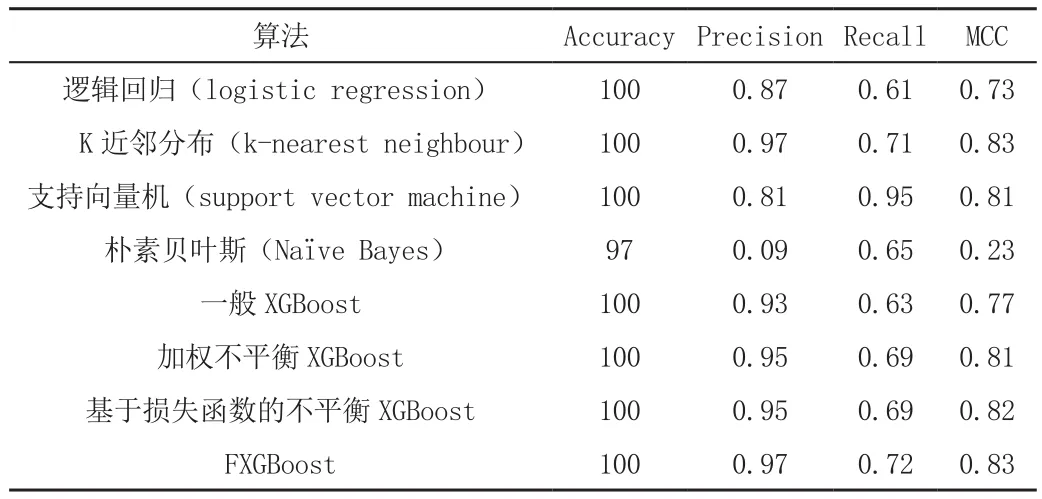
表6 场景3中各算法的评估

5 结论

本文提出了一种基于改进的损失函数的XGBoost模型（FXGBoost）来解决不平衡数据集问题。该方法是受到加权二元交叉熵的启发，根据参数的不平衡性，基于WCEL不平衡参数进行了改进，并采用加权评分公式对其进行评分。在实验中，我们使用ULB机器学习组数据对信用卡诈骗问题进行分类。实验结果表明，该方法比现有其他机器学习方法在处理不平衡数据集上更加有效。