逆韦布尔分布下n中取k系统的随机比较

郭玉琦，吕卫东，夏春蒙

(兰州交通大学 数理学院，兰州 730070)

随机序是指随机变量在一定数学意义下,进行的“大小”比较.在不同的应用背景下,研究者定义了各类不同的随机序关系[1-3].随机序在可靠性理论、生存分析、经济、保险等许多领域都有重要的应用.在各类随机变量分布中,许多学者研究了随机变量服从伽马分布、指数分布、几何分布、威布尔分布等的随机序之间的相互关系[4-7].但目前为止对服从逆韦布尔分布的随机变量在各种随机序中的比较关系却不多见.

本文将致力于研究随机变量服从逆韦布尔分布的随机序之间的相互关系.在此之前,张娅莉等[8]研究了两个相互独立且服从逆韦布尔分布的随机变量在一般随机序、似然比序、失效率序以及凸序之间的相互关系.邱国新等[9]研究了在独立的随机变量服从寿命参数不同但形状参数相同的逆Weibull分布下，所组成的两个串(并)联系统中,失效率序、反向失效率序、色散序、占优序和p-阶大序之间的相互关系.本文在此基础上进一步研究了在特征寿命参数不同，形状参数不同或特征寿命参数相同和形状参数不同的逆韦布尔分布下,串联系统下的分散序关系,并联系统下的洛伦茨序、星序和失效率序之间的相互关系.

1 预备知识

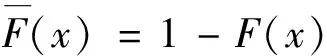
定义1随机变量X服从逆韦布尔分布,其分布函数和密度函数分别为

(1)

(2)

其中：α和β分别是特征寿命参数和形状参数，记作X～IW(α,β)[10].

定义2

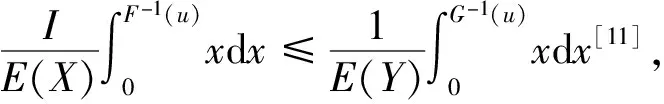
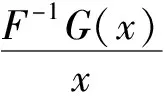
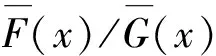
4)如果F-1(β)-F-1(α)≥G-1(β)-G-1(α)成立,0≤α<β≤1,则称X在分散序意义下大于等于Y,记作X≥dispY.

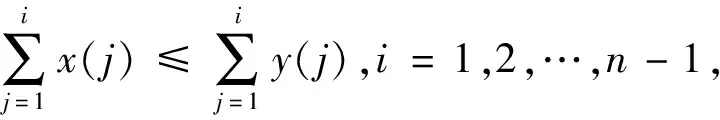
引理1将α=F(x)代入定义4)中得到G-1(F(x))-x是递增的，那么则称X在分散序意义下大于等于Y,记作X≥dispY[12].

引理2一个可微函数φ(x)是S-凸(S-凹)的，如果当且仅当i≠j时，有

2 主要结论

2.1 串联系统

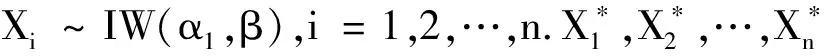
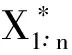
X1∶n的反函数是

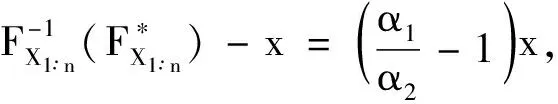
2.2 并联系统

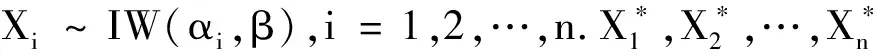
证明：Xn∶n分布函数是

反函数是

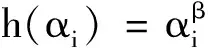
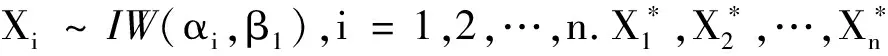
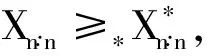
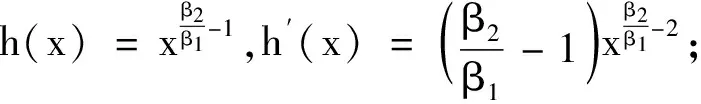
当0<β1<β2,h′(x)>0.

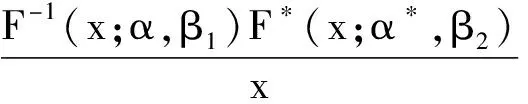
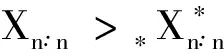
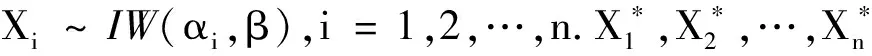
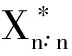
首先,证明φ(x)是递增的

当r>λ时,x>0,φ′(x)>0;

其次,要证明φ(x)是递增的

即

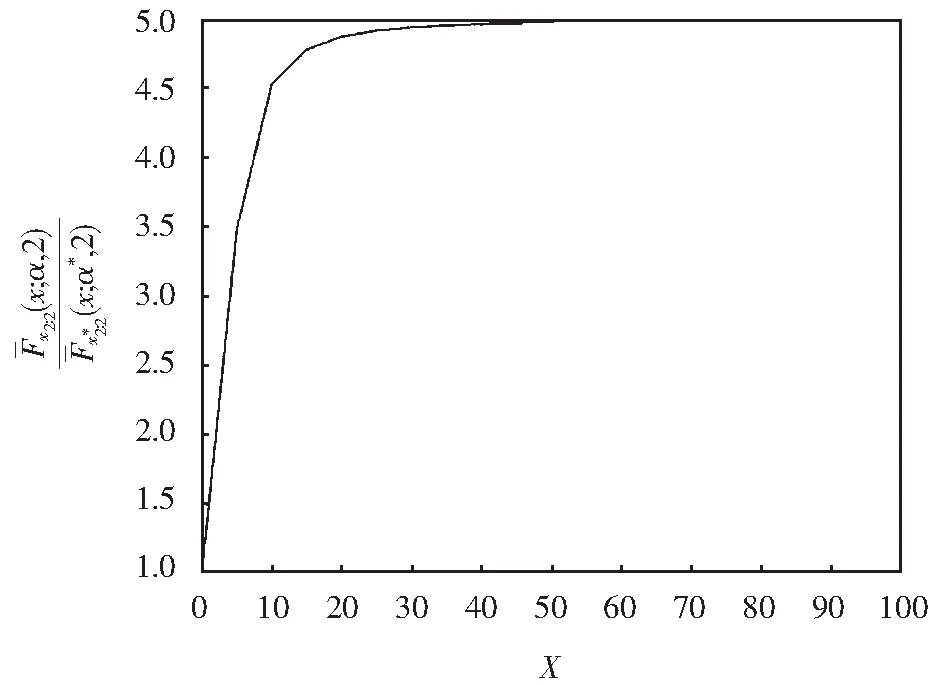
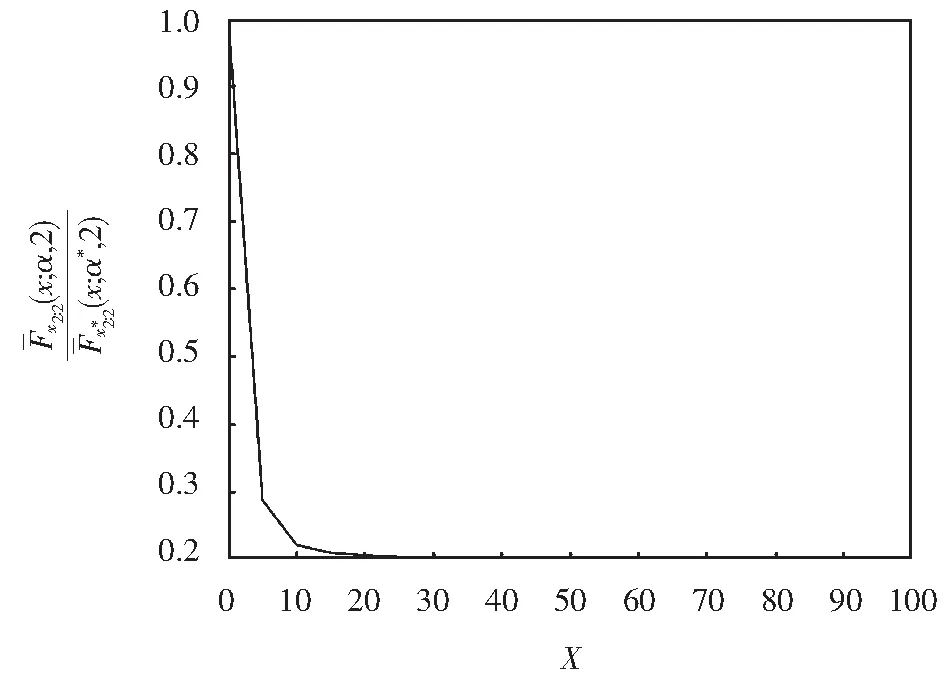
rerx-β-re(λ+r)x-β<λe(λ+r)x-β-λeλx-β;rerx-β+λeλx-β

所以φ′(x)>0,当x>0,φ(x)是递增的;

又因为φ(x)>0,φ(x)>0;

图1 递增失效率序

图2 递减失效率序