基于遗传算法的柴油机空气系统优化研究
2022-02-15姜光,张欣
姜 光, 张 欣
(北京交通大学 机械与电子控制工程学院,北京 100044)
在改善发动机动力性、经济性与排放性方面,空气系统起着至关重要的作用,因此对发动机空气系统的优化很有必要。然而柴油机性能参数的优化问题是一个非线性、多约束的优化问题,优化的过程需要确定优化参数、优化目标,并满足各种约束条件,且各参数之间存在耦合关系[1]。传统的优化算法诸如蒙特卡罗法、黄金分割法、梯度下降法等很难解决发动机参数优化问题。
近年来,遗传算法在内燃机工程领域内有许多成功的应用,如在电控发动机标定中的应用[2]、在发动机各部件结构参数优化中的应用[3-4]、在发动机故障诊断中的应用[5]、在发动机建模中的应用[6]以及在发动机各控制参数优化中的应用等。在发动机控制参数优化研究中,文献[7]以最低指示燃油消耗率为目标,对柴油机喷油正时、喷油脉宽、进气温度、增压压力等发动机运行条件进行优化,采用遗传算法KIVA代码进行预设的优化后,燃油消耗率降低了35%;文献[8]采用遗传算法分析某四冲程高速直喷式柴油机进气压力、喷油定时、喷孔直径化及废气再循环(exhaust gas recirculation,EGR)率,使得NOx和PM排放均明显下降,优化结果完全满足排放法规标准;文献[9]基于 Matlab 编写遗传算法程序,以 NOx排放为目标,以原机的Soot 排放与输出转矩为约束条件,通过 Matlab 与 GT-Power 的联合仿真对 EGR 参数与喷油参数进行了优化;文献[10]以排气温度、缸内废气比例和爆震强度等为约束条件,优化发动机空燃比和喷油等参数,结果表明在4 000 r/min时燃油消耗率最高可降低4.82%。
目前提高发动机燃油经济性的研究中,关于喷油参数及燃烧参数的研究较多,而对空气系统参数的研究较少。本文将遗传算法应用于空气系统控制参数优化标定中,利用GT-Power与Matlab/Simulink仿真模型,对某带有EGR系统的涡轮增压柴油机的空气系统进行优化。优化结果表明,利用遗传算法对柴油空气系统寻优可以有效降低柴油机的燃油消耗率。
1 优化目标与优化参数
本研究对商用车柴油机空气系统进行优化,优化变量为可变截面涡轮增压系统(variable geometry turbocharger,VGT)叶片开度以及废气再循环系统EGR阀门开度,优化目标为在满足排放标准的条件下各个工况下的有效燃油消耗率最低。
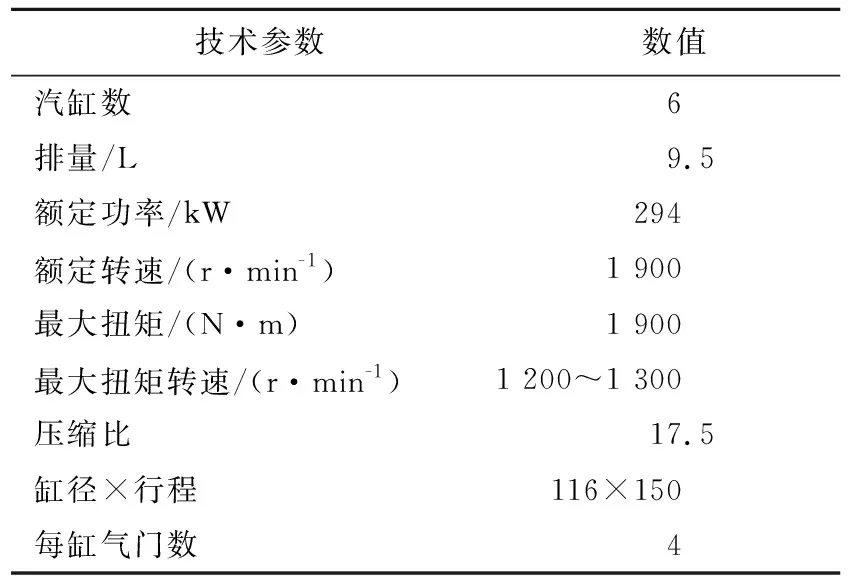
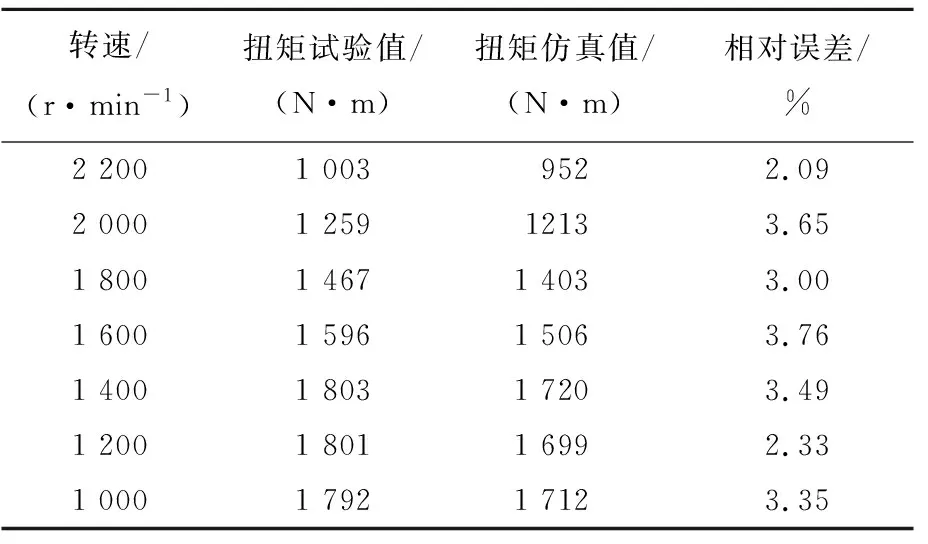
本研究不考虑柴油机的后处理过程,即以柴油机缸内燃烧后的原始排放为约束条件。柴油机空气系统性能参数优化问题表示如下:
maxbe(n,T,Ar,xv),
n=nobj,
T=Tobj,
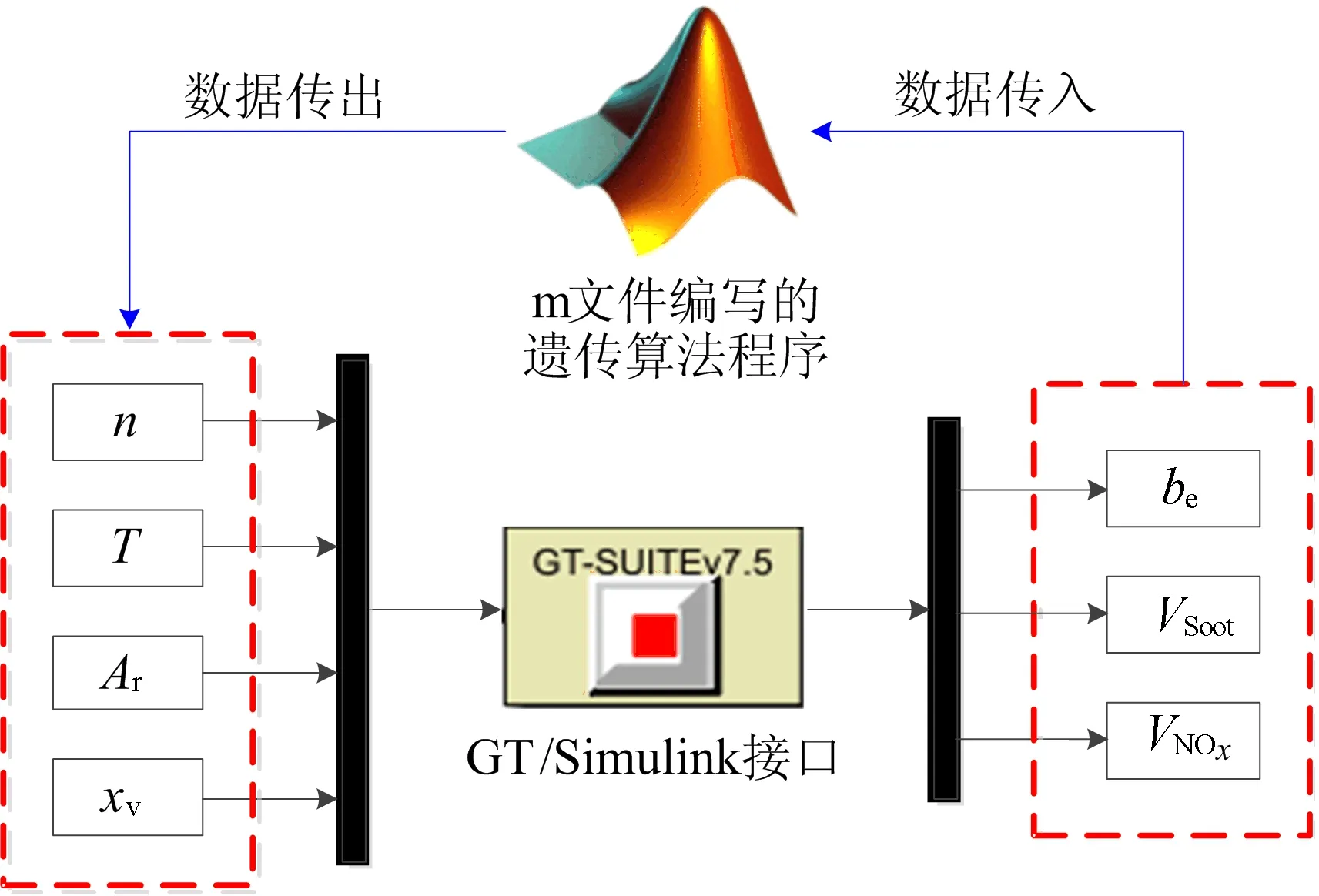
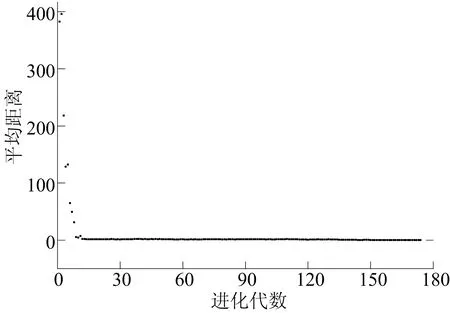
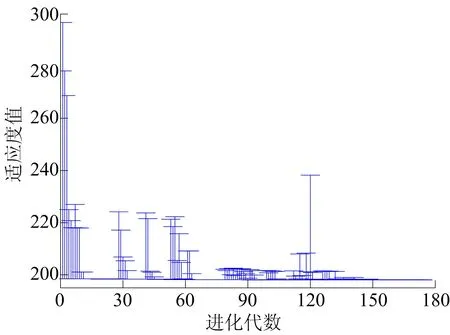
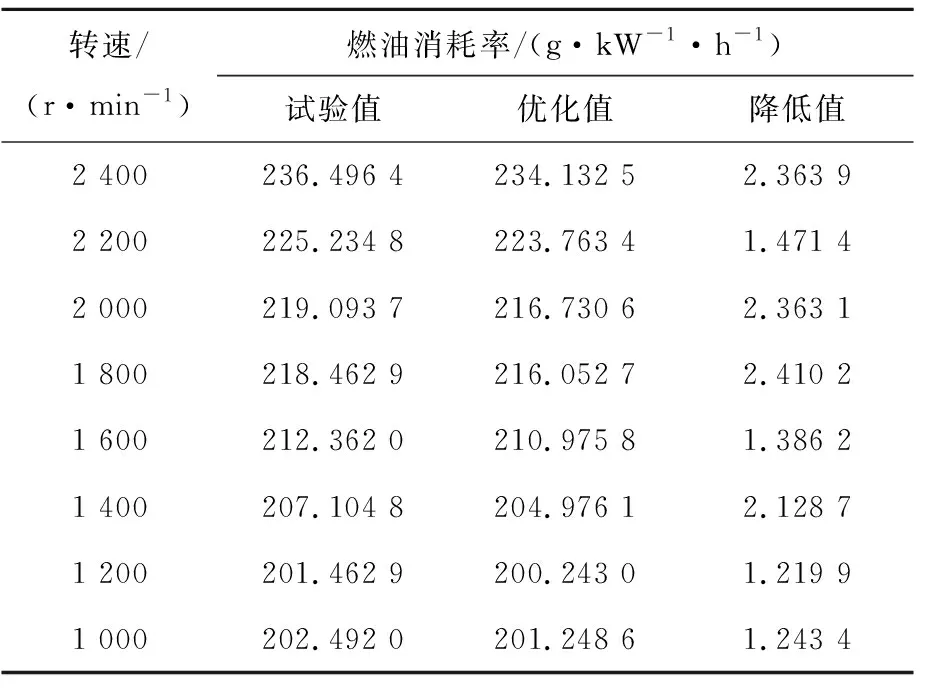
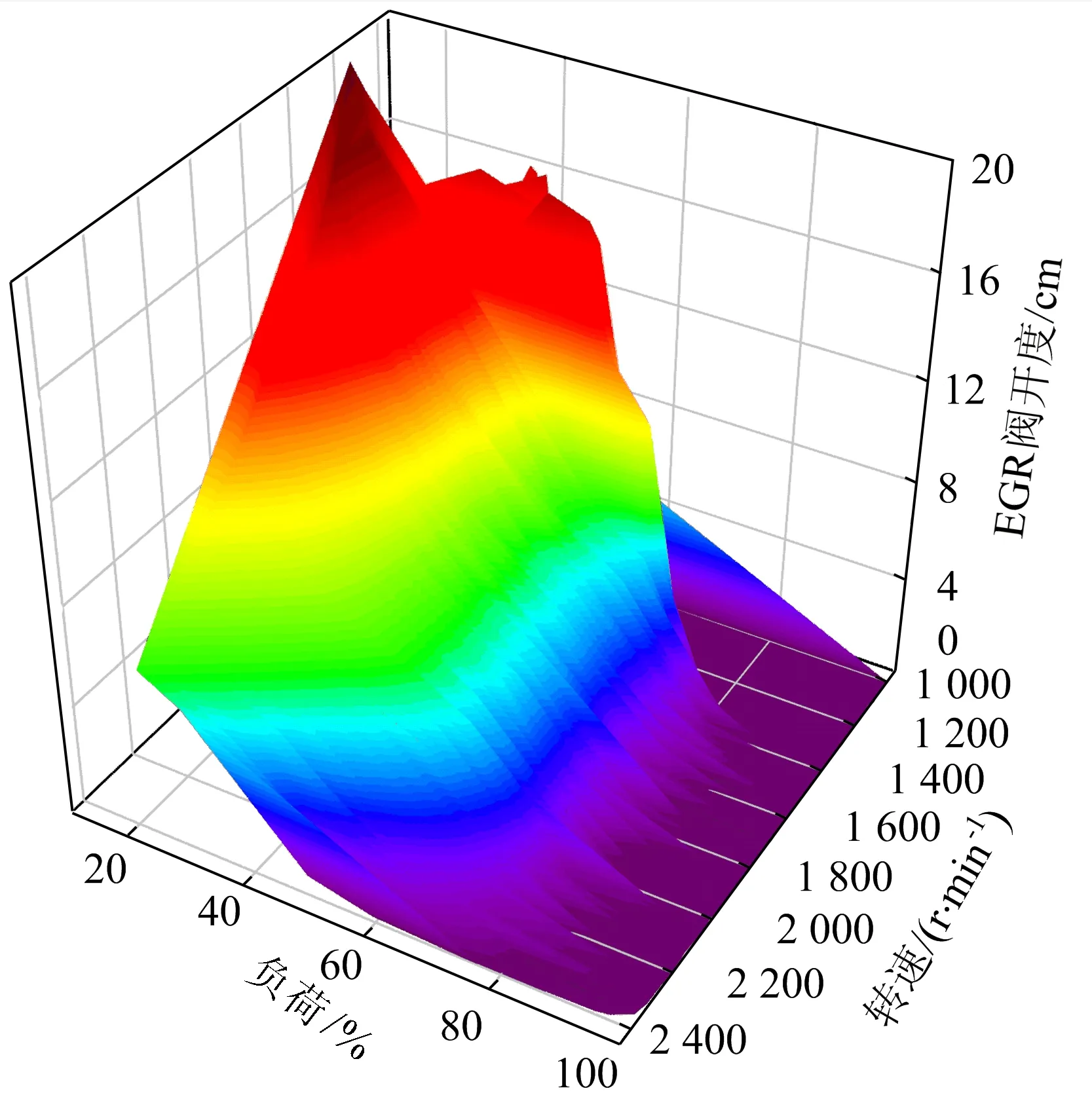
0 0≤Ar≤20, VNOx(n,T,Ar,xv)≤5 700, VSoot(n,T,Ar,xv)≤66 (1) 其中:be为发动机有效燃油消耗率;n为发动机转速;T为发动机负荷;xv为VGT叶片开度的位置;Ar为EGR阀门开度;VNOx为NOx排放量;VSoot为Soot排放量。 本研究所采用的发动机为某国产增压中冷商用车发动机[11],气缸排列形式为直列,其主要技术参数见表1所列。 表1 国产某款发动机主要技术参数 利用GT-Power,根据原机参数建立带有VGT系统与EGR系统的柴油机仿真模型。设置仿真时间最小为20个工作循环,当仿真结果满足收敛条件后,停止仿真,求解方法为显式求解。 根据厂家提供的柴油机台架试验数据,对全负荷工况下的柴油机输出扭矩及功率进行了验证,结果见表2、表3所列。 表2 扭矩试验值与仿真值的对比 表3 功率仿真值与试验值的对比 验证结果表明,在全负荷工况下,仿真结果与试验结果基本吻合。其中,扭矩的最大相对误差为3.76%,功率最大相对误差为3.78%,两者均不超过5%。这说明所搭建的模型可以用于柴油机性能仿真。 对GT-Power仿真模型进行标定后,建立Matlab/Simulink与GT-Power联合仿真程序示意图,如图1所示。 图1 GT-Power与Matlab/Simulink联合仿真模型示意图 程序具体工作流程描述如下: (1) 在m文件中,对某一转速及负荷条件下的EGR阀开度及VGT叶片开度2个控制参数设定范围,并对以上所有数据进行编码。 (2) 在m文件中进行种群初始化。包括定义种群规模、定义进化代数、各操作算子等。 (3) 在m文件中,利用sim函数调用Simulink程序,并将种群中的每个个体(每个个体中包含转速等4个参数)依次传递到Simulink中。 (4) Simulink中的数据通过接口传递到GT-Power中,GT-Power进行计算,仿真得到有效热效率、VNOx和VSoot的计算结果,通过接口传入到Simulink中,Simulink将数据传入到m文件中。 (5) 当该种群中的所有个体计算完成后,m文件中的遗传算法程序根据各数据计算适应度值进行选择、交叉和变异操作,产生一个新的种群。 (6) 重复步骤(3)~步骤(5),若遗传算法的停止标准被满足,则算法找到该工况下的满足排放条件的最小有效燃油消耗率及所对应的EGR阀开度和VGT叶片开度。 (7) 转到下一个工况,重复步骤(1)~步骤(6),直至所有设定的工况计算完成后停止优化。 本文利用英国谢菲尔德大学开发的GATBX工具箱进行遗传算法设计。编码形式采用二进制编码,遗传操作算子分别为遍历抽样选择算子、两点交叉算子、mutbga变异算子;交叉概率选取为 0.66,变异概率选取为 0.001;群数量为 150,初始种群通过试验设计(design of experiment,DOE)方法产生。遗传算法程序终止条件为连续10代中相邻两代最优解之间相差小于1%,且最大迭代次数为250次。 研究中通过引入罚函数的方法处理VNOx和VSoot排放2个约束条件设计目标函数。对约束条件进行归一化处理得: g1(x)=VNOx/5 700-1 (2) g2(x)=VSoot/66-1 (3) 其中,x=(n,T,Ar,xv)。 采用遗传算法解决本研究优化问题中的目标函数,表示如下: (4) 采用联合仿真平台,对柴油机全负荷工况点进行寻优。以转速在1 400 r/min下的工况为例,优化结果如图2~图4所示。 图2 1 400 r/min全负荷工况下每代个体之间的平均距离 图3 1 400 r/min每代个体适应度的最佳值与最差值 图4 1 400 r/min全负荷工况下最后一代个体适应度值分布 图2所示为每一代种群中的所有个体之间的平均距离,平均距离越小,表示种群中个体间的差别越小。随着进化过程的增加,性能较差的个体被逐步淘汰,较好的个体不断保留,当进化到第119代时,种群中的个体都趋近于最佳值,种群间个体的平均距离最终接近于0,停止进化。 图3中的误差线表示每一代个体适应度的最佳值与最差值。随着进化过程中的不断淘汰,每一代中的最佳值与最差值的差距逐渐减小,到最后一代时,如图4的个体适应度值分布图所示,最终种群所有个体的适应度值均在203.975 5~203.977 0之间。在最后一代,寻优得到的最低燃油消耗率为203.976 1 g/(kW·h),对应的EGR阀开度为0,VGT叶片开度为0.21。 全负荷工况下优化后的燃油消耗率见表4所列。从表4可以看出,经遗传算法优化后,全负荷工况下的燃油消耗率比原机燃油消耗率均有下降。发动机转速为1 800 r/min时,优化后燃油消耗率比未优化前降低了2.410 2 g/(kW·h);各转速下所优化的工控点燃油消耗率的降低幅度均在1.21~2.42 g/(kW·h)之间,这表明通过遗传算法对空气系统寻优可以有效提高柴油机的经济性。 表4 全负荷工况下燃油消耗率优化结果 对发动机进行其他负荷工况寻优,分别选取发动机转速为1 000、1 200、1 300、1 400、1 500、1 800、2 100、2 400 r/min,负荷为10%、20%、30%、40%、50%、60%、70%、80%、90%,共72组工况。结合之前优化的全负荷工况,利用插值的方法做出优化后的EGR阀开度map与VGT叶片开度map,结果如图5、图6所示。 图5 EGR阀开度map 图6 VGT叶片开度map 从图5可以看出,总体上低转速和低负荷时EGR阀开度较小,高转速和高负荷时EGR开度较大。从理论上分析,在发动机低负荷时,为了减小污染物的生成,使用较大的EGR率;在发动机高负荷时,为了保证发动机的动力性与经济性,采用较小的EGR率或不采用EGR。高转速时,为了保证发动机的新鲜空气冲量,采用较低的EGR率。 从图6可以看出,低转速和高负荷时VGT叶片开度较小,高转速和低负荷时 VGT叶片开度较大。从理论上分析,当发动机转速减小时,VGT叶片开度减小,涡轮转速增加,增压压力变大,保证低转速时的增压压力与进气流量;在发动机转速增加时,采用较大的叶片开度,防止增压器超速导致增压器损坏。在发动机负荷增加时,采用较小的VGT叶片开度,保证增压器有较大的转速,提高增压压力与进气量。 (1) 本文利用Matlab/Simulink与GT-Power联合仿真程序,并结合遗传算法对柴油机空气系统进行了优化。优化结果表明,利用遗传算法可以对柴油机空气系统进行有效寻优,在全负荷工况下的燃油消耗率相较于原机下降幅度为1.21~2.42 g/(kW·h),遗传算法用于空气系统优化可有效降低柴油机燃油消耗率。 (2) 根据各个工况的寻优结果,利用插值的方法做出优化后的EGR阀开度map与VGT叶片开度map。通过分析map图可知:在发动机高负荷和高转速时,宜采用较大的EGR率;在高转速和低负荷时,宜采用较大的VGT叶片开度。2 空气系统优化研究
2.1 联合仿真程序的开发

2.2 遗传算法的设计

3 优化结果分析
3.1 全负荷工况下寻优结果分析

3.2 部分负荷工况寻优结果分析

4 结 论
