基于局部势场Ａ算法和动态窗口法的农用轮式机器人路径规划

刘顺 闫荣兰 台浩娇 姜春阳 许立成 王克凯

摘要：针对未知农业生产环境中，现有移动机器人路径规划方法实时性差和适应性弱等问题。在视觉传感器实时定位和地图构建的基础上，提出一种混合规划方法用于农用轮式机器人。在全局路径规划中使用局部势场A*算法进行路径规划，在局部路径修正中使用改进的动态窗口法进行路径修正。通过仿真将提出的混合路径规划方法与传统路径规划方法进行比较，验证该方法的优越性和鲁棒性。结果表明，相对于传统路径规划方法，混合路径規划方法通行代价降低63.89%，在保持最大偏移不变的情况下，搜索时间节省27.01%。该混合路径规划方法可以实现未知环境的规划路径，有很好的壁障和路径规划能力，具有一定的应用价值。

关键词：移动机器人;局部势场A*算法;动态窗口法;混合路径规划方法;视觉传感器

中图分类号：S24;TP242   文献标志码： A

文章编号：1002-1302（2022）02-0192-06

收稿日期：2021-05-17

基金项目：河北省青年科学支持基金（编号：18HB01661）。

作者简介：刘 顺（1988—），男，河北正定人，工程师，主要从事农业自动控制等研究。E-mail：hbjyls@126.com。

随着农业智能技术的不断发展，农业机器人领域越来越受到重视。它是一种以农业生产任务为主要目的，同时具有信息识别、路线识别、人工智能等前沿技术于一身，可以解决大量农业生产力的不足[1]。轮式移动机器人以其运动稳定灵活、能耗低、结构简单等优点，在农业领域广泛应用[2]。农业机器人可以利用自动导航技术实现施肥、喷洒和除草等智能农业作业，而路径规划是自主导航的重要基础。因此，对农用轮式机器人的路径规划方法进行研究具有重要的现实意义。近年来，国内外对轮式移动机器人的路线规划方法进行了大量的研究，并获得许多优异的成果。李凤玲等提出一种适用于未知环境的路径规划方法，通过相机获取周围环境信息，通过萤火虫算法进行路径规划，以帮助机器人找到最佳路线并避免障碍物，仿真结果表明该算法具有有效性和实时性[3]。吴东林等设计一种基于人工势场法的采摘机器人动态路径规划系统，并对系统方法进行仿真分析，发现该系统优化效果明显，具有良好的避障和路径规划能力[4]。雷蕾等提出一种基于启发式搜索算法的自动拣选机器人路径规划方法，通过改进的A*算法进行路径规划，发现改进的A*算法可以明显改善采摘机器人的行进路径，并使规划路径更平滑[5]。李国辉提出一种用于农业机器人的壁障路径智能规划方法，通过分析农用机器人的运动系统结构和定位原理，建立农用机器人的运动模型，完成避障路径规划的结构设计，将模糊控制算法用于合理规划农业机器人的避障过程，发现农业机器人可以成功避开障碍物[6]。上述研究存在算法复杂、内存开销大、实时性差等问题，但这些研究仍为农业轮式机器人的路径规划方法提供了理论依据。本研究提出一种混合路径规划方法用于农用轮式机器人。全局路径规划使用局部势场A*（local potential field A*，LPF-A*）算法，而局部路径校正使用自适应参数动态窗口方法（adaptive parameters dynamic window approach，APDWA），应用混合规划算法可以有效避开周围的障碍，找到最优到达目标点的路径。

1 系统结构

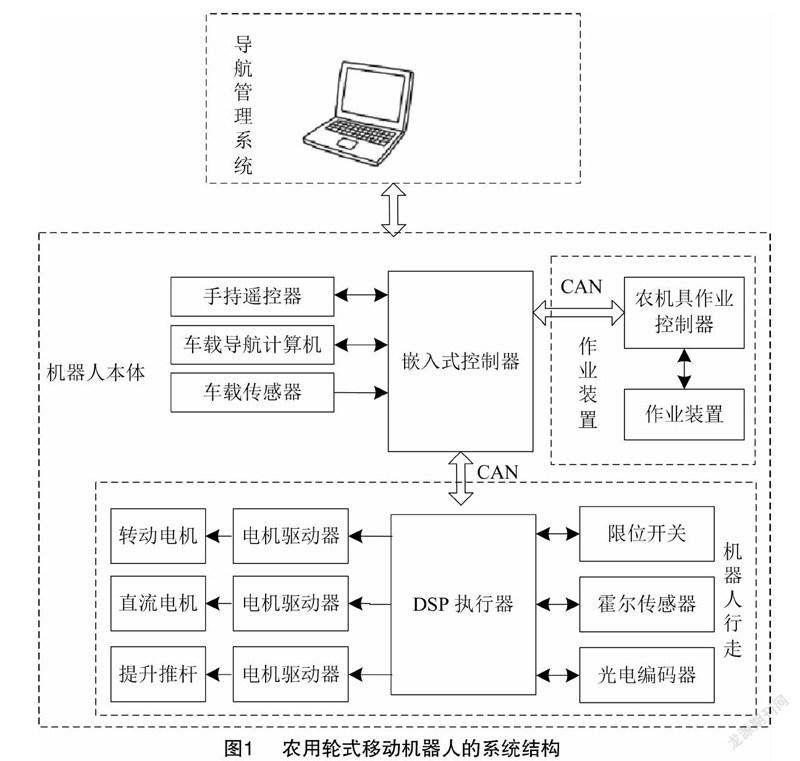
农用轮式移动机器人路径规划方法的设计与移动机器人测试平台密不可分，因此，本研究须要建立一种可在农业环境下运行的轮式移动机器人的原型[7]。轮式移动机器人原型采用开放式结构和控制系统，可安装不同的农具进行不同的作业。图1为农用轮式移动机器人的系统结构，该系统分为导航管理系统和机器人主体2个部分。导航管理系统具有远程控制机器人的功能，但侧重于设置机器人的自主运动参数、自主作业并监视机器人的运动状态。机器人主体由控制系统、行走部分和操作装置3个部分组成，负责分解、协调和执行任务[8]。

2 混合路径规划方法

机器人环境用栅格法表示[9]。在生成的栅格地图中，全局路径规划使用LPF-A*算法，而APDWA算法用于局部障碍物碰撞检测和局部路径修改。

2.1 LPF-A*全局路径规划

2.1.1 A*算法原理

A*算法通过启发式函数对路径的代价进行估算，采用代价最低的节点作为下一个扩展节点[10]。代价函数为

f（n）=g（n）+h（n）。（1）

式中：f（n）表示搜索节点的代价函数;g（n）、h（n）分别表示实际代价值（起点-搜索节点）和评估代价值（搜索节点-终点）。

A*算法运行时，有2个列表（open和close），未访问的节点在open列表中，已访问的节点在close列表中[11]。具体算法步骤如下：步骤1，当前节点为起点，加入close列表，设open列表为空。步骤2，确定当前节点是否为目标节点。如果是，则规划完成[12];如果不是，请继续下一步。步骤3，获取与当前节点相邻的8个节点位置，并在每个节点上执行以下操作。（1）判断节点是否加入close列表。如果是，则忽略;如果不是，请继续下一步。（2）判断节点是否加入open列表，如果是，则重新计算g值。如果g值小于原始值，则用父节点替换当前节点，对g值和f值重新计算，转到步骤4，否则继续下一步。（3）创建1个新节点，并计算新节点的g值、h值和f值，用父节点替换当前节点[12]。步骤4，在open列表中找到f值最小的节点，并将其分配给当前节点（current_node）。步骤5，当前节点加入close列表，对open列表进行判断，为空则固化失败，否则转到“步骤2”。该算法的流程见图2。

启发式函数的选择是A*算法成功的关键[13]。启发式函数的估计值与实际值越接近，代价函数越准确，且A*算法规划的路径越适合实际环境。

本研究使用8个邻域路径搜索算法，父节点可以搜索8个相邻子节点。如果相邻节点之间的距离为d，则对角节点距离为2d。本研究采用的启发式函数如下[14]

h（n）=2min[d1（n），d2（n）]+|d1（n）-d2（n）|。（2）

式中：d1（n）、d2（n）分别表示当前节点与目标节点的横坐标、纵坐标之差。

为了找到通行代价最低的路径，须要结合先前的局部势场函数S（n），并将其引入代价函数f（n）中，从而获得更安全有效的路径。代价函数变换见公式（3）[15]

f（n）=g（n）+h（n）+ωS（n）。（3）

式中：ω表示权重因子，值越大，则搜索节点离障碍物越远，但整體搜索路径越长。

2.1.2 栅格地图优化

Elfes最早提出栅格地图模型[16]。环境中的障碍模型用网格占有率表示，此方法广泛应用于路线规划系统[17]。建立水平x轴和垂直y轴的直角坐标系xOy（图3），设环境带下为w×h，每个栅格的边长为a，x、y轴栅格数分别为 nx=w/a、ny=h/a。常用的栅格表示方法包括序列号方法和直角坐标系法。

传统的栅格图模型仅使用二元函数来划分环境图中的障碍区域和可执行区域。对于机器人而言，规划的路径只能在可行区域。在这种情况下，A* 算法采用最短路径方式通过障碍物，但由于尺寸、误差等原因，存在一定的碰撞风险[18]。

为了解决上述问题，采用人工势场对栅格进行优化。通过对邻域内障碍物数进行计算，可以得到空闲节点的局部障碍物势场函数[19]。

S（n）=k，0≤k≤m。（4）

式中：m表示搜索邻域范围，设置为m=8，采用8个邻域路径搜索;k表示可搜索邻域中占用的栅格节点数。

2.2 混合路径规划算法

DWA算法可以通过局部障碍物信息获得最优的无碰撞路径。但该方法在长距离规划中极易出现局部极小值。LPF-A*算法的全局路径规划中，轨迹由大量栅格节点组成。都视为局部目标点，移动机器人会出现左右反复旋转的现象。因此，机器人在移动时需要执行许多转向运动，控制无法做到精确。

本研究结合LPF-A*算法和APDWA算法进行混合路径规划。具体的实现过程如下：步骤1，提取关键点，如果对多有节点进行局部规划，会导致计算量大和结果轨迹的曲率大，所以需要提取关键节点进行目标搜索，关键节点提取的基本原理是确定当前节点是否与上一个和下一个目标在同一条直线上。如在一条直线上，则认为该点沉余，继续遍历整个路径。只保留起始点、目标点和关键点。步骤2，约束方位角。基于单个目标点进行搜索可能会发生碰撞。因此，提出一种自适应全局最优路径代价函数[20]。

G（v，w）=α·localhead（v，ω）+β·dis（v，ω）+γ·vel（v，ω）;（5）

α=a·kphead（v，ω）+b。（6）

式中：localhead（v，ω）表示预测轨迹终点和下一个关键点之间的方向夹角;kphead（v，ω）表示拐点是轨迹终点与下一个关键点之间的方向夹角;α、β、γ表示各函数相对应的加权系数;dis（v，ω）表示轨迹点到障碍物的最小距离;vel（v，ω）表示当前轨迹速度;a、b表示缩小α范围的固定参数。

规划算法流程图见图4。

3 仿真结果与分析

3.1 仿真参数

通过对全局优化算法和混合优化算法进行仿真比较，可以验证算法的优越性。试验中使用的计算机是Intel i5处理器，8 g内存和Win10系统，并使用MATLAB 2018a软件进行仿真。在栅格图中，黑色网格节点是障碍节点，白色网格节点是空闲节点。根据势场函数的值，使用MATLAB的colormap函数标记从红色到紫色的势场函数。对于有局部障碍物存在的空闲节点，红色势场最大，紫色势场最小。β=0.9、γ=0.2、T=3 s、a=0.4、b=1。

3.2 全局规划算法仿真分析

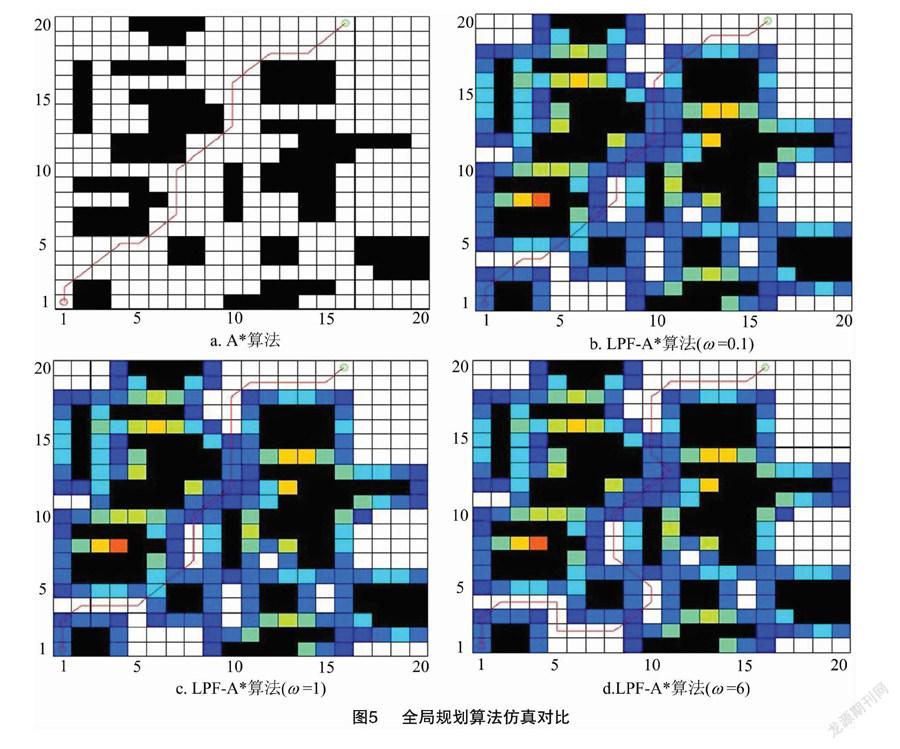
本研究选择的试验环境是20 m×20 m的栅格图，分析 LPF-A*算法在不同ω参数（0、0.1、1、6）下获得的路径图，ω=0即为A*算法。传统A*算法和LPF-A*算法之间的比较见图5，全局规划算法仿真结果见表1。

由图5可知，带有红色圆圈的栅格是起点，带有绿色圆圈的栅格是目标点。 ω的增加使得路径通行代价更低，但路径长度增加。

由表1可知，ω=6通行代价最低，但是总路径长度却明显增加。这是因为对于多个障碍而言，本研究选择绕行策略而不是穿越，在不改变路径长度的情况下，可以大幅降低通行成本。另外，本研究基于A*算法添加局部势场，这会稍微增加搜索时间和通行节点的总数。

3.3 混合算法仿真分析

本研究采用全局算法得到的关键栅格节点序列生成全局最优路径节点，使用APDWA算法实时避障和局部路径修改。并对该规划方法进行仿真分析，选择ω=6的最低通行代价。图6为静态环境下调整α值（1、5、自适应）的仿真结果，红色轨迹为全局规划，蓝色轨迹为混合规划。

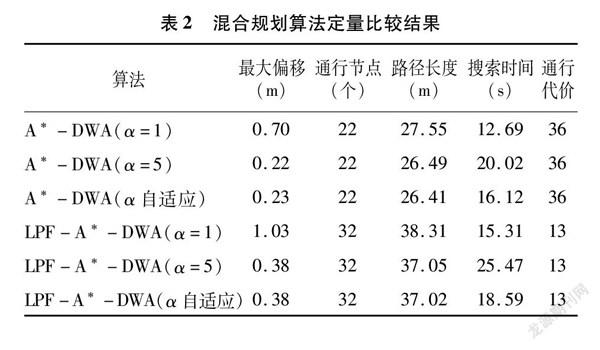
由图6可知，混合算法可以实现攻台壁障。由表2可知，与A*-DWA算法相比，本研究规划方法通行代价降低了63.89%。在保持最大偏移不变的情况下，搜索时间可以节省27.01%。将动态障碍物添加到原始静态障碍物环境中，以验证算法的鲁棒性。动态障碍物仿真结果见图7。

由图7可知，本研究规划方法不仅可以满足全局最优轨迹，还能够根据环境中的动态障碍物修改局部轨迹，以实时避开障碍物。

4 结束语

本研究提出一种基于LPF-A*算法和APDWA算法的农用轮式移动机器人混合路径规划算法，仿真验证了混合规划算法的优越性和鲁棒性。第一，全局路径规划使用LPF-A*算法，而局部路径使用APDWA算法，该混合规划算法遇到静态障碍和动态障碍时可以有效地避开周围的障碍，找到最优到达目标点的路径。第二，将本研究算法与未改进前的A*-DWA算法进行比较，结果显示，本研究算法可以将通行代价降低63.89%，在保持最大偏移不变的情况下，搜索时间可以节省27.01%。考虑到当前的试验设备和数据规模，本研究仍处于起步阶段，因此逐步改进和完善将是下一步的重点。

参考文献：

[1]李 瑞，敖 雁，孙启洵，等. 大田农业物联网应用现状与展望[J]. 北方园艺，2018（14）：148-153.

[2]刘国斌，车宇彤. 农业信息化与农业现代化融合发展研究[J]. 情报科学，2019，37（1）：148-155.

[3]李凤玲，陈 珊，范兴江，等. 基于萤火虫算法动态未知环境的路径规划[J]. 自动化与仪表，2019，34（6）：53-58.

[4]吴东林，张玉华. 采摘机器人动态路径规划系统研究——基于人工势场法[J]. 农机化研究，2019，41（6）：219-223.

[5]雷 蕾，石 晨. 基于启发式搜索算法的自动采摘机器人路径规划研究[J]. 农机化研究，2021，43（7）：240-244.

[6]李国辉. 农业机器人避障路径智能规划研究[J]. 农机化研究，2021，43（3）：236-239.

[7]王铭铭，徐 浩. 基于物联网的安徽省农田灌溉实时监测及自动灌溉系统研究[J]. 节水灌溉，2017（1）：68-70，75.

[8]余国雄，王卫星，谢家兴，等. 基于物联网的荔枝园信息获取与智能灌溉专家决策系统[J]. 农业工程学报，2016，32（20）：144-152.

[9]白秋产. 基于物联网的农田智能灌溉系统[J]. 江苏农业科学，2017，45（22）：247-251.

[10]朱洪清，于利娟，汪烨欢，等. 基于物联网的太阳能远程精准灌溉系统的研制和应用[J]. 中国农机化学报，2014，35（2）：246-249.

[11]Liu G M，Ouyang M G，Lu L G，et al. Analysis of the heat generation of lithium-ion battery during charging and discharging considering different influencing factors[J]. Journal of Thermal Analysis and Calorimetry，2014，116（2）：1001-1010.

[12]Krewer U，Rder F，Harinath E，et al. Review-dynamic models of Li-ion batteries for diagnosis and operation：A review and perspective[J]. Journal of the Electrochemical Society，2018，165（16）：3656-3673.

[13]Patel G K，Dabhi V K，Prajapati H B.Clustering using a combination of particle swarm optimization and K-means[J]. Journal of Intelligent Systems，2017，26（3）：457-469.

[14]Gautam J V，Prajapati H B，Dabhi V K，et al. Empirical study of job scheduling algorithms in hadoop MapReduce[J]. Cybernetics and Information Technologies，2017，17（1）：146-163.

[15]Caetano C E F，Lima A B，Paulino J O S，et al. A conductor arrangement that overcomes the effective length issue in transmission line grounding[J]. Electric Power Systems Research，2018，159：31-39.

[16]吴宇豪，安籽鹏. 面向图像三维重建的无人机航线规划[J]. 計算机技术与应用，2019，45（3）：76-79，87.

[17]苏海锋，许道林，李汶江，等. 基于改进蚁群A*算法的输电线路路径搜索[J]. 河北大学学报（自然科学版），2017，37（1）：92-100.

[18]王庆斌，石亮缘，黄 辉，等. 基于改进粒子群算法的输电线路路径规划研究[J]. 广东电力，2018，31（9）：135-141.

[19]刘先正，温家良，潘 艳，等. 采用改进粒子群算法的直流电网最优潮流控制[J]. 电网技术，2017，41（3）：715-720.

[20]王 毅，刘 波，何 宇，等. 果园移动机器人路径识别系统[J]. 传感器与微系统，2020，39（9）：69-72.